基于貝葉斯分層模型的可違約債券利率期限結構

吳建華 張穎 王新軍

(1.濟南大學數學科學學院，山東 濟南 250022；2.山東大學經濟學院，山東 濟南 250100)

引言與文獻綜述

無論是微觀金融資產定價、金融風險管理和投資分析，還是宏觀經濟預測和貨幣政策制定，利率期限結構都發揮著極其重要的角色。國債收益率曲線從一個側面反映了實體經濟、金融市場的狀況和市場主體對經濟未來的預期信息。而可違約債券的利率期限結構則在風險管理中被用于推測企業債券的信用評級和評估衍生品的風險。因此，對于利率期限結構的準確估計和預測研究一直是學界和業界的熱點問題。現代利率期限結構模型研究大致可以分為如下三類模型：經驗估計模型(包括樣條擬合模型和參數擬合模型)，仿射期限結構模型(包括均衡模型和無套利模型)和宏觀-金融模型。以上這些研究方向都從不同的角度對利率期限結構展開了豐富的研究。最早利用統計學方法對利率期限結構進行經驗估計的文獻可以追溯到McCulloch and Huston(1971)[1]和McCulloch(1975)[2]，他們將貼現曲線模型化為多項式基礎函數的一個線性組合，分別利用二次和三次多項式樣條模型來擬合收益率曲線。在此基礎上，Schaefer(1981)[3]提出了利用Bernstein多項式模型化收益率曲線的思路。不過多項式樣條函數會引起遠期利率的劇烈波動，為此Vasicek and Fong(1982)[4]提出指數樣條模型，它可以有效避免遠期利率的劇烈波動，獲得更為平滑的遠期收益率曲線。類似的，Shea(1984)[5]提出了B-樣條模型，Fisher et al.(1995)[6]提出了平滑樣條模型。以上這些方法主要采用分段曲線對收益率曲線進行擬合，因此被統稱為樣條類模型。另外一些學者采用了整段曲線對收益曲線進行擬合的思路，即所謂的參數化擬合模型，比如Nelson and Siegel(1987)[7]提出的Nelson-Siege模型，以及在NS模型基礎上，Svennson(1994)[8]提出的Svennson模型。針對已有的這些參數模型，Bliss(1997)[9]提出了交叉效度方法檢驗這些模型的有效性。再后來，Diebold and Li(2002)[10]基于NS模型提出了動態NS(DNS)模型，估計了不同時刻刻畫收益率曲線水平、斜率和曲度的三個因子。周子康等(2008)[25]提出了NSM模型，他們通過對指數多項式添加擴展項，調整了收益率曲線的形狀，既保留了NS類模型的經濟學含義和參數的穩健性，也克服了NS類模型的單峰特征。張蕊等(2009)[26]通過在DNS模型中引入第四個因子，建立了四因子的動態NS利率期限結構模型，利用Kalman濾波方法處理了非線性最優化問題。在模型的應用方面，王志強和康書隆(2010)[27]針對經典的NS模型在實際應用中存在部分久期配比免疫問題，提出利用收益率預期信息對模型進行動態調整的思路，從而改進了NS模型的應用。在模型的估計方面，De Rezende and Ferreira(2014)[11]提出了利用分位數回歸估計擴展的Nelson-Siegel模型的方法。沈根祥和陳映洲(2015)[28]通過在DNS模型中引入新的斜率因子，從而構造了雙斜率的DNS利率期限結構模型，提高了模型對短期收益率的靜態擬合和動態預測績效。尚玉皇等(2015)[29]通過對DNS模型進行擴展，構建一種混頻Nelson-Siegel模型。張雪瑩等(2017)[30]在Diebold et al.(2006)[12]提出的動態Nelson-Siegel模型中，通過引入政府債券的供給和需求變量，討論了國債供求關系、利率期限結構與宏觀經濟變量之間的變動關系，構建了含有國債供求變量的動態Nelson-Siegel模型。目前這兩類利率期限結構的經驗估計方法已經被業界的Bloomberg和Reuters的電子信息系統所采用。

從模型擬合所采用的債券數據類別來看，以上的研究幾乎都是基于政府債券數據來估計無風險利率的期限結構，相比而言，針對可違約債券利率的期限結構估計的研究相對較少。尤其是國內的相關研究更少，一個重要的原因就是，無論是從發行量還是從發行規模上來看，可違約債券都相對落后于發達的國債市場，從而相應的數據也較少，對于某些期限較長的可違約債券來說，發行數量更少。根據中國債券市場數據顯示，2015年中國債券市場各券種未結清數量占比分別為政府債34.62%，銀行債16.52%，公司和企業債5.12%，金融類企業短期融資券22.77%，其他債券20.97%。顯然，相比政府債券，可違約債券(公司債和企業債)在未結清的數量方面相形見絀1。

從現有的文獻來看，最早研究企業債券的利率期限結構估計的是Schwartz(1998)[13]，他提出先用信用評級作為分類標準，將所有的企業債券劃分成不同的組別，然后構建每一組內債券的利率和期限之間的變動關系。不過這種估計思路有一個較大的缺點：組內樣本容量較小。這就使得對收益率曲線估計的精度較低，表現為曲線的平滑度較低。為了增加組內的樣本容量，Houweling et al.(2001)[14]和Jankowitsch and Pichler(2002)[15]提出了對企業債券和政府債券的進行聯合建模的思路，充分利用政府債券發行量較大的優點，以增加樣本容量，這樣針對每一個信用評級水平，都可以生成信用價差曲線的估計量，而且可以獲得更為平滑的收益率曲線。Krishnan et al. (2010)[16]沿著Diebold and Li(2006)[10]提出的參數化方法，基于發行公司作為分類標準對債券進行分類，利用指數多項式來模型化價差曲線的差。在此基礎上，Jarrow et al. (2012)[17]基于樣條的模型將企業債務的期限結構描述為無風險期限結構和一個價差曲線的和，然后利用非線性最優對模型參數進行了估計。雖然后面這幾個研究通過增加政府債券來提高樣本的容量，從而改進了模型估計的精度，不過這僅僅是一種權宜之計，對于單純估計可違約債券利率期限結構的研究，仍然有待進一步探索。為了克服可違約債券的利率期限結構估計中出現的某些組內樣本數據較少的問題，本文提出了利用貝葉斯分層模型(Gelman et al. 2013)[18]對所有的分組進行聯合估計的思路。貝葉斯分層模型在生物、心理學和教育學等社會學科中應用廣泛，它特別適用于參數多于樣本點的情形。從現有的研究來看，將貝葉斯分層模型引入到利率期限結構估計中的研究思路幾乎還是一個空白，本文試圖在這一方面進行探索。

本文首先在Svensson利率期限結構模型框架內，構建可違約債券價格的貝葉斯分層模型，并給出分層Dirichlet后驗分布估計的MCMC算法的具體實現過程。其次，利用中國債券交易所市場的債券數據對貝葉斯分層模型和經典的單曲線模型進行了對比實證分析。最后，提出了貝葉斯分層模型在各種利率期限結構研究中的應用前景。

模型構建及其估計方法

債券的利率期限結構是指在相同的違約風險水平下，在某一時刻，不同的到期期限與對應的零息債券到期收益率之間的關系。債券利率期限結構的經驗估計是指以零息債券的市場價格為基礎，找到某個平滑函數來擬合某一時點的債券利率與不同期限之間的變動關系。不過市場上大多數債券都是附息債券，零息債券較少，因此需要通過某種方法從附息債券價格中推導出零息債券的到期收益率。基本的思路為：附息債券可以看作是一系列不同期限零息債券的組合，附息債券的價格應該等于復制其現金流量的所有零息債券的價值的總和。因此，可以用零息債券的利率期限結構來計算附息債券的價格。根據零息債券和附息債券的這種關系，可以利用實際市場中的付息債券的價格倒推出零息債券的利率期限結構。

一、擬合函數與權重的選擇

考慮n只同等信用質量的附息債券，記tmi為第i只債券的到期日，其中i=1,2…,n，在債券有效期內需要多次支付現金流(利息或本金)C(i,j)，支付時刻為ti,j(＞t)，其中j=1,2…,mi，mi為第i只債券的最大支付次數。根據現金流貼現原則，第i只附息債券在當前時刻t的理論價格P(t,tmi)可以如下計算：

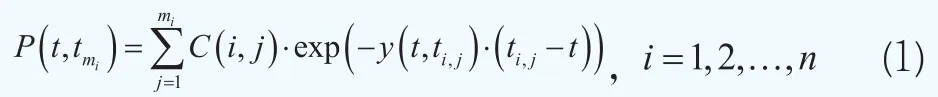
其中y(t,ti,j)表示第i只債券在時刻ti,j的到期收益率。假設g(t,ti,j;θ)為備選的近似函數，其中θ為待估計參數向量。那么P(t,tmi)的估計值為

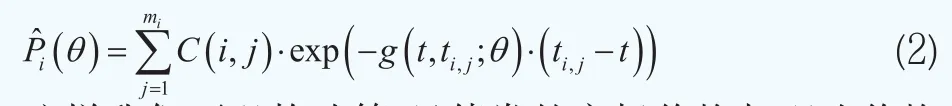
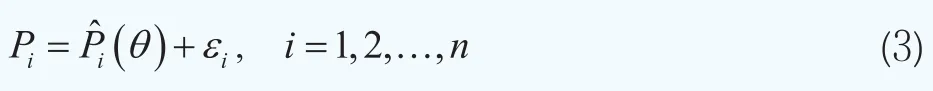
這樣我們可以構造第i只債券的市場價格與理論價格之間的非線性回歸模型其中Pi為第i只債券的市場價格，為債券的理論價格，εi是誤差項，假設滿足εi～N(0,τ-1)，其中τ為精度(逆方差)。在二次損失函數準則下，使得下面的目標函數最小時的參數向量即為待估計參數向量θ的最優值：

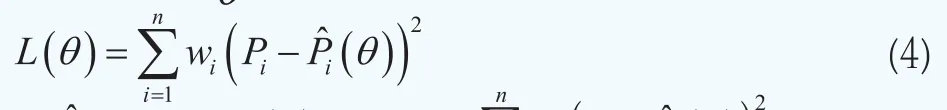
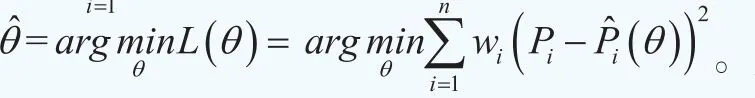
即其中Pi和分別為第i只債券在當前時刻t的市場價格和理論價格，wi為第i只債券在定價誤差中所占的權重，引入權重的目的是對定價誤差中的異方差進行調整，在后面我們會專門討論如何基于久期構造權重指標。以上的估計思路可以稱之為加權非線性最小二乘準則。顯然，模型估計的關鍵點有兩個：一是選擇何種與期限T有關的參數函數g(t,T；θ)來近似收益率曲線y(t,T)；二是如何構造權重指標wi，i=1,2…, n。

本文選取g(t,T；θ)為Svensson(1994)[8]函數以對收益率曲線y(t,T)進行整體逼近，即：

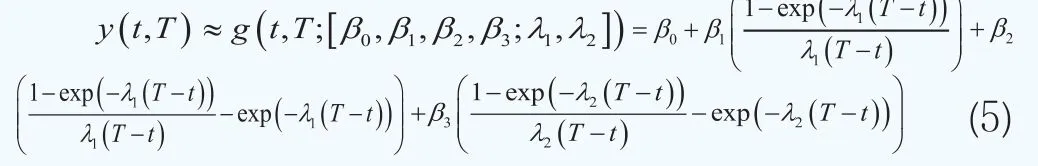
其中θ=(β0, β1, β2, β3)為形狀系數，λ=(λ1, λ2)為縮減因子系數。Svensson函數是由Svensson(1994)[8]在Nelson-Siegel函數基礎上提出的，它可以生成在實踐中經常見到的一個較為寬泛的曲線的形狀，曲線形狀完全由四個參數所決定。β0刻畫了利率的長期趨勢，β1刻畫了利率的短期行為，β2和β3描述了利率的中期行為，這兩個參數共同決定了曲線的曲率和極值點的特征。這些參數使得利率期限結構的曲線更為靈活多變，它可以刻畫水平型、單調型、V型、倒V型和駝峰型的曲線形狀。

對于權重的選擇。債券到期日的長短會影響到用于推測期限結構的信息量。基于久期綜合了利率、期限和價格的信息可知，利率的變化對長期債券價格的影響要遠大于對短期債券價格的影響。而在模型參數的估計中，最小化過程會減少定價誤差的異方差，如果直接最小化誤差平方和會導致長期收益率相對于短期收益率的過度擬合，從而降低收益率曲線短期部分的擬合效果。因此，在不考慮其他因素的情況下，應當對不同期限的債券賦予不同的權重。這樣在最小化目標函數(4)中我們引入了一個權重wi，它表示第i只債券在定價誤差中所占的比重，即

引入權重wi后，權重會按比例調整誤差項的方差，即(τwi)-1。

接下來的問題就是如何量化權重wi。Bolder and Streliski(1999)[19]認為，既然債券的久期綜合了到期收益率、價格和期限三者的信息，那么利用久期定義的權重可以將這些信息融合進估計的過程中。下面在不考慮其他因素的情況下，我們沿用該思路將第i個債券的權重定義為

其中Di為第i只債券的麥考利久期。麥考利久期是Macaulay(1938)[20]在全美經濟研究局(NBER)的一次研究報告中提出的，它是利用債券現金流的現值作為權重的債券的到期日的加權平均值。具體的計算公式如下

其中Ci為t時刻需要支付的現金流，T為債券到期日，r為到期收益率。這樣，在一組債券中，對于具有較短到期日的哪些債券來說，權重將趨于更高。

上面給出的利率期限結構估計的靜態模型，可以用于政府和企業債券的期限結構的估計。在具體應用的時候，通常假設政府債券都有同樣的期限結構。企業債券因為具有不同的違約風險水平，通常會根據某些分類準則將企業債券劃分成不同的族群，然后對每一族群分別估計它們的期限結構。在實踐中，一個流行的分類準則就是債券的信用評級。

二、利率期限結構的貝葉斯分層模型

在利用上述的單曲線估計方法對可違約債券進行估計時，經常會面臨小樣本問題，即在某些分組中，只有少數幾只債券。這在債券市場上一個常見的現象，尤其在中國不發達的債券市場上這種問題更為嚴重。顯然，在單曲線估計方法下，小樣本問題會導致組內的估計精度會大幅度降低。為了克服小樣本帶來的估計精度較低的問題，本文提出了整體聯合估計的貝葉斯分層模型的思路，通過對所有債券分組的期限結構進行聯合建模，來抵消組內樣本數量較少的問題，從而提高估計的精度。

實際上，在貝葉斯分析框架內估計利率期限結構模型的思路并不新鮮，Li and Yu (2005)[21]早就提出了在利用貝葉斯分析框架來估計利率期限結構模型的思路。不過從估計思路來看，他們的方法仍然屬于單曲線估計方法，而本文則采用了多層先驗分布和聯合估計的方法思路。另外，他們利用樣條函數來分段刻畫收益率曲線，本文采用的是收益率曲線的參數函數整體擬合方法。

假設根據K個不同的信用級別把所有的企業債券劃分成K組，這對應著需要估計K個不同的期限結構。令θK為刻畫第k個期限結構的參數向量，那么需要對參數向量θ={θ1, θ2,…θK}進行估計。為了克服可能會出現的個別組內樣本容量過小的問題，將參數向量θ設定多層先驗分布，構建貝葉斯分層模型，這樣就可以利用所有K組債券的信息對參數向量θ進行聯合估計。

債券價格的貝葉斯分層模型主要包括下面的三個部分：

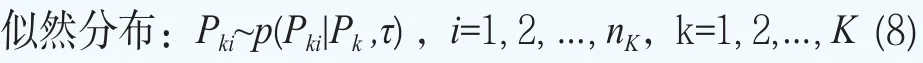
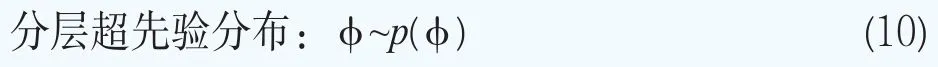
其中Pki為第k個分組中第i只債券的價格，其中i=1,2,…,nk，nk表示第k組中包含nk個債券，k=1, 2,…,K。

債券價格的似然函數分布P(Pki|θk ,τ)(i=1, 2,…,nk，k=1,2,…,K)由下面的非線性回歸給出，即債券的市場價格被模型化為Pki=(θk)+εki，其中εki是誤差項，假設滿足εki～N(0,τ-1)，其中τ為精度(逆方差τ=1/σ2)。該式等價的概率模型為

其中P^i(θk)為第k組債券中的第i個債券的理論價格，根據式子(2)可知有如下形式

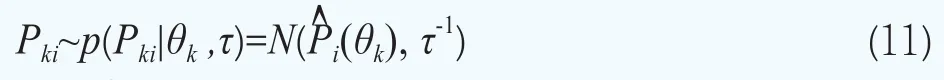
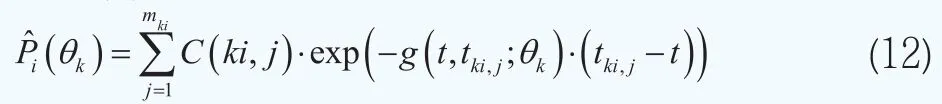
C(ki,j)為第k組債券中的第i個債券在時刻為tki,j(t＜ti,j＜mki)所支付的現金流(利息或本金)，j=1, 2,…,mki，mki為第i只債券的最大支付次數；g(t,tki,j；θk)被用于近似描述在時刻t的K個待估計的期限結構的第k個期限結構，這樣每一個期限結構都通過一個四維向量θk=(βk0, βk1, βk2, βk3)來刻畫。在上面的設定下，我們可以得到債券價格的似然函數p=(Pki|θkτ)(i=1, 2,…,nk，k=1, 2,…,K)。

為了估計模型參數θk，本文設計了一個有限混合先驗分布，以保證模型能夠捕獲特定主體參數之間的異質性(包括異常點，超擴散點和多樣態)。比如對于某些投資級的債券，由于某種原因導致這些債券的市場價格變得很低，這些債券應當被降級為垃圾級，如果這些債券的評級并沒有及時發生改變，就會出現異常點。在數據概率建模中，對于數據的不同局部具有不同的變化特征時，單參數分布族無法給予確切地描述，但有限混合分布模型卻能對其進行有效的刻畫，而且有限混合分布模型具有良好的適應性和模擬性，它廣泛的被應用于生物、基因工程、信息科學和金融保險等社會各領域。比如混合泊松分布在醫學和保險精算領域有廣泛應用；混合指數分布在信息工程領域里有一定應用；而正態混合分布應用更是廣泛，理論證明任何有限分布都可以由等協差陣的有限正態混合分布任意逼近，而且正態混合分布模型也具有較高的靈活性和高效性的計算優勢。關于正態混合分布更為詳細的相關內容可以參考Yu and Deng(2015)[22]。

在貝葉斯分層模型中，將參數向量θk的先驗分布設定為正態混合分布可以提高完全后驗推斷中的計算效率。我們用一個正態混合分布來模型化期限結構參數向量θk的分布p(θk|φ)，即

這樣超參數可以寫成φ={G}。貝葉斯模型的分層更多的是體現在對超參數φ={G}的分布的設定。下面沿用文獻Müller and Quintana(2015)[23]的方法給出超參數φ={G}的超先驗分布的設定。設G服從Dirichlet過程，即G～DP(G0，M)，其中基礎分布G0服從多元正態分布，即G0～N(b，B)，它刻畫了位置參數G的均值，M服從伽馬分布和M～Ga(am，bm)，它決定了G圍繞G0波動大小的程度。矩b和B被選擇為與混合核是共軛的：b～N(b0，B0)和B-1～Wishart(r，(rW)-1)。對于精度τ，設定它服從伽馬分布，即τ～Ga(aτ，bτ)。

綜上所述，債券價格的貝葉斯分層模型如下給出：

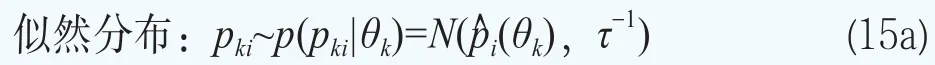
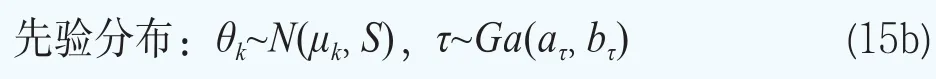
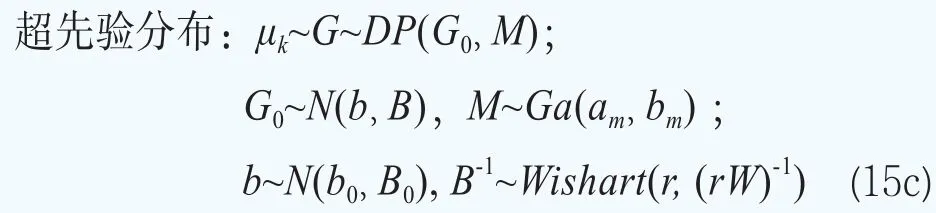
在本文設定的先驗分布的超參數中，混合基礎測度G0和協方差矩陣S對于所有的參數θk都是一樣的。這樣后驗分布推斷就可以利用所有期限結構共享的信息。

通過設定位置超參數G服從Dirichlet過程的先驗分布，貝葉斯分層模型可以借用整個期限結構的力量，對每一個分組中的少數幾個債券的期限結構進行聯合建模，從而可以有效解決組內樣本數量較少所帶來的估計精度不足的問題。

顯然，上面給出的貝葉斯分層模型的后驗分布沒有封閉解。利用MCMC算法從后驗分布中進行抽樣，可以獲得參數的貝葉斯估計的近似解。令K為待估計的期限結構的個數，nk為期限結構k(k=1,2…,k)中的債券的個數。下面給出模型的MCMC算法。

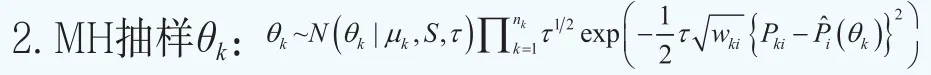
因為θk的后驗分布沒有封閉形式，需要利用Metropolis-Hasting算法更新θk。令θtk為第t次迭代時的當前點，θ*k為從替代分布q(θ*k|θtk)模擬的候選值。替代分布設為其中sd和ε為正的常數，t0是一個正整數，cov表示經驗協方差矩陣。在本文中，我們令sd=0.5，ε=0.00001，t0=2000。該算法提供的適應性允許我們生成精確的估計量，即使我們對重要性分布的協方差矩陣設定了一個粗糙的近似。

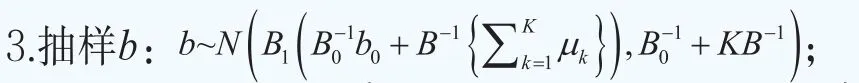
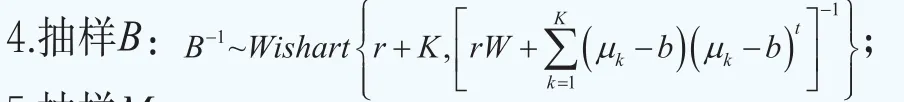
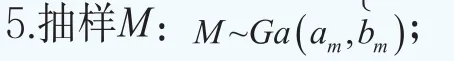
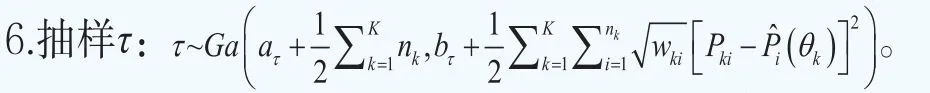
沿用文獻Müller and Quintana(2004)的思路，對初始值和超參數做如下的設定。超參數為初始值為對于MH算法，為了對θk進行升級，我們設定其中和分別為參數θk的樣本均值和樣本協方差矩陣。

實證結果及分析

一、樣本選取

本文所使用的數據是從和訊網債券債券行情抓取的2017年4月6日15∶00更新的交易所市場的債券交易數據，選取的變量主要包括：信用評級、本金、息票率、到期日、剩余年限、息票支付日、修正久期和最新報價。

債券樣本的信用評級主要包括投資級債券(AAA,AA,A,BBB)，最大到期日為15年。我們排除了具有負的收益的所有債券，因為這些債券具有極差的流動性。最后樣本數據集包含了國內248只未結清的企業債券的數據，基于信用評級的分類包括四組：AAA,AA,A和BBB；每一組中分別包括49、179、13和7只債券。

表1 基于信用評級的債券的分布情況

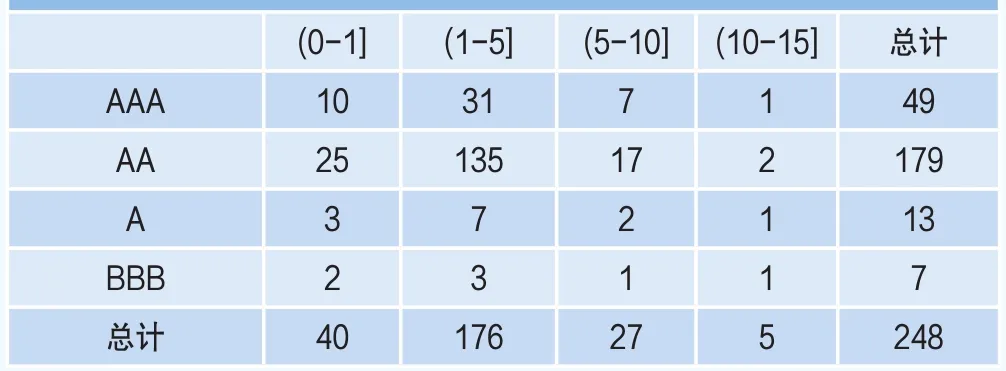
表2 基于剩余年限(列)和信用評級(行)的債券的分布情況

為了進一步考察到期日與債券個數的關系，表2給出了將剩余年限劃分成了下面幾組：

表2表明，債券的個數對于1年期以上的中長期債券來說，隨著時間增長，債券的個數急速減少，比如，在剩余期限為1～5年的區間中有176只債券，它解釋了樣本中債券數量的71%。而在10以上的區間中，債券的個數只有1只。顯然，剩余期限越短，債券的流動性越強，這可以部分的解釋投資者對中短期債券更加偏好的流動性偏好理論。

本小節將上面的債券價格貝葉斯分層模型方法用于估計企業債券的期限結構。為了進行對比，本節也將利用單曲線方法對不同的期限結構進行估計。

二、實證結果及分析

1. 利率期限結構估計

單曲線方法利用現金流貼現原理估計得到基于信用評級的期限結構。在本文提出的利率期限結構的貝葉斯分層模型中，利用了作者自己編寫的非線性似然函數程序，結合R軟件包“DPpackage”和“termstrc”對模型進行了估計，軟件包“DPpackage”專門針對貝葉斯非參數和半參數模型，利用模擬抽樣技術從后驗分布中抽樣，其中的先驗分布為服從Dirichlet過程的分層先驗分布。本文通過最小化(4)中的加權平方誤差來估計參數，權重由(6)定義，最優化問題利用了R軟件中的nlminb()函數進行數值計算。

在利率的期限結構估計中，第k個期限結構的參數被估計為參數向量θk的后驗均值，它由后驗樣本的平均值來近似。

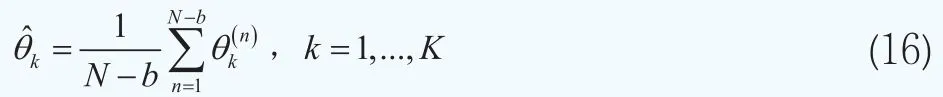
其中N為MCMC算法中的抽樣迭代的次數，b為MCMC算法中的預燒期，K為期限結構的個數，在本文中K=4。對于精度參數τ也有類似的估計結構。

被估計的參數列在表3中，其中所有參數的馬氏鏈路徑最終都收斂在一定的區域里，波動比較平穩，且沒有明顯的周期性和趨勢性。針對不同的信用級別，利用該方法都獲得了相應的參數估計。利用可替代的初始值，在所有情形中的被估計參數都與表3中報告的數值基本一致。

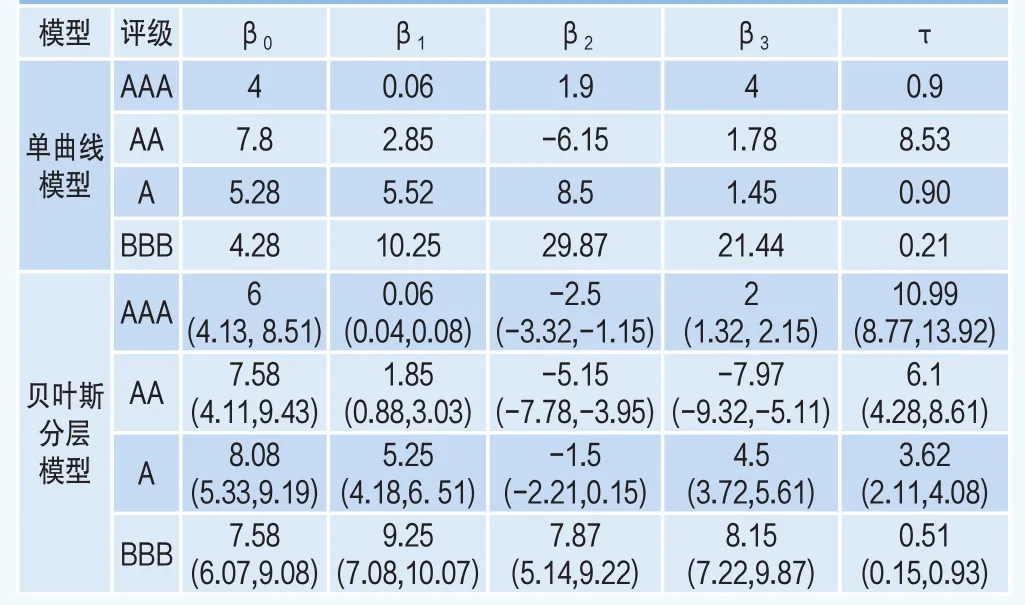
表3 基于信用評級分類的期限結構的被估計參數

為了進行對比，估計量的表達沿用了Nelson and Siegel(1987)[7]引入的原始參數化思路。對于利用貝葉斯分層模型獲得的估計量，在括號中給出了估計量的90%的置信區間。

圖1給出在四個不同的信用級別(AAA,AA,A,BBB)下的期限結構估計，給出了期限結構估計的單一曲線方法和貝葉斯分層模型估計。

從圖1可以看出利用單曲線模型估計的利率期限結構時，AAA級和AA級表現出了較為合理的曲線形狀，即到期日越長，收益率越高。但是A級和BBB級的收益率曲線表現出了與現實和理論不符的嚴重問題，比如A級和BBB級的收益率曲線不但表現出了不合理的隆起形狀，甚至在長期，A級和BBB級收益率曲線竟然低于AA級的收益率曲線，這顯然與信用級別越低，收益率越高的理論和現實相矛盾。如果探究其出現估計與現實出現較大偏差的原因，一個重要的原因就是，A級和BBB級的債券數據樣本容量較小帶來的估計偏差，比如A級債券的樣本個數為13，BBB級債券的樣本個數為7。

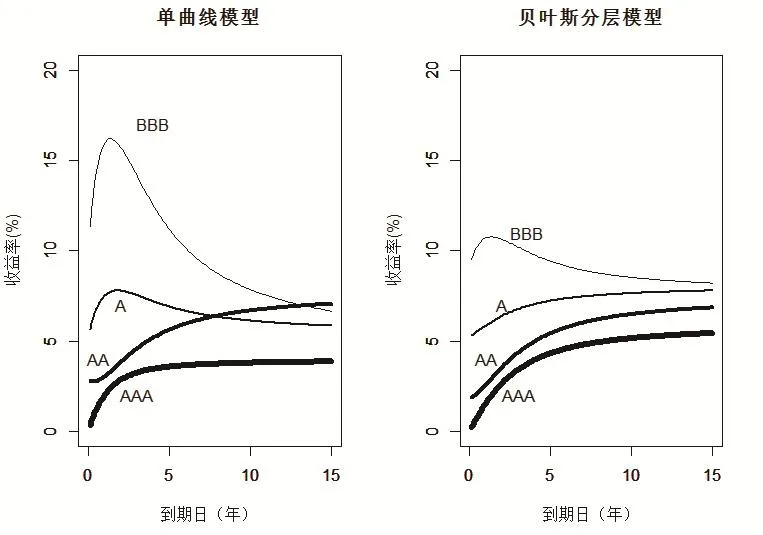
圖1 基于信用評級分組的收益率曲線

相比而言，基于貝葉斯分層模型所估計的收益曲線則表現出了與現實和理論相一致的形狀，它們的“順序”與理論一致，這和信用風險和收益之間的預期關系是一致的：信用評級越低，收益越高。

從圖1的對比可以證明，貝葉斯分層模型可以有效的克服個別分組內樣本點過少所帶來的估計精度偏低的缺點，而且估計結果現實，理論模型與流動性偏好理論基本一致，即投資者更加偏好短期債券，可以接受較低的收益率，而對于到期日較長的中長期債券，則會索取更高的收益率，以彌補可能發生的各種風險。

2. 模型估計的績效分析

期限結構估計模型的績效通過樣本內和樣本外預測作為標準進行對比。樣本內的擬合優度根據價格殘差(價格誤差)進行度量，價格殘差也叫價格誤差，它等于市場價格減去債券的理論價格，理論價格由被估計的貼現曲線計算而得。對比價格殘差是合適的，因為期限結構模型應該能夠精確的解釋市場價格，因為利率是債券價格的主要決定因素。具有最低價格誤差的期限結構模型給出了最好的擬合。

樣本預測績效的計算利用了Steeley(2008)[24]提出的交叉效度分析。交叉效度的基本做法是，將數據集合劃分成兩個互補的子集訓練集合和測試集合，首先利用訓練集合來擬合期限結構，然后利用得到的期限結構計算測試集合中的每只債券的理論價格，接著根據市場價格算出價格殘差，最后計算測試集合的根均方預測誤差(RMSPE)和平均絕對預測誤差(MAPE)見圖2。

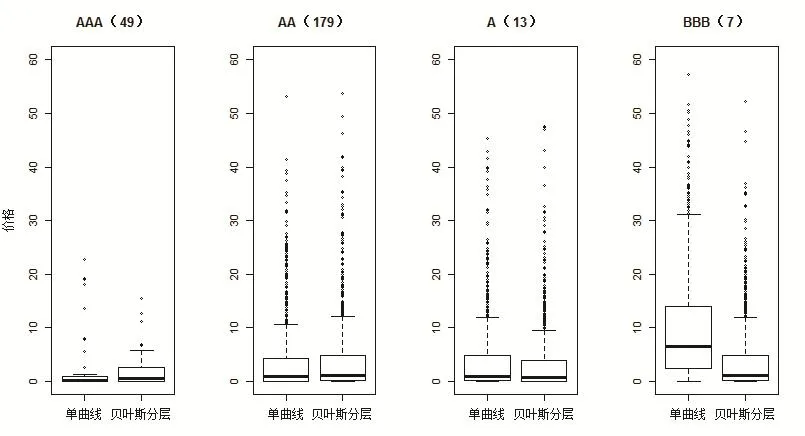
圖2 單曲線和貝葉斯分層模型估計的樣本內絕對價格誤差

表4 平均RMSPE和MASPE

另外，在圖2的箱線圖和表5中，我們也給出了單曲線模型和貝葉斯分層模型估計的債券價格的樣本預測績效。

從圖2和表4可以看出，貝葉斯分層模型和單一曲線估計量給出了價格估計的類似的樣本內預測績效。對于較低的信用評級，中位數和四分位數間距(IQR)都會上升。不過，貝葉斯分層模型的估計量的中位數絕對價格殘差要小于單一曲線方法的殘差。這說明，貝葉斯分層模型估計績效要高于單曲線模型的估計績效。

將分層貝葉斯模型用于基于信用評級的債券分組的期限結構的估計的最大好處是，由分層貝葉斯模型估計的收益曲線與經濟理論相符。而且貝葉斯分層模型不會受到異常值的過度的影響：其中的DP先驗分布允許異常值具有自己的聚集類，因此會獨自離開主要的族群。通過將所有的債券保留在樣本內，可以避免引入偏倚。

結論

本文探討了如何利用貝葉斯分層模型估計可違約債券利率的期限結構的方法，通過對參數設定分層Dirichlet先驗分布，可以對所有評級分組的參數進行聯合估計，這樣可以利用不同信用評級債券之間共享的信息，克服了單曲線模型面臨的某些分組內的小樣本所引起的估計精度較低的問題，從而可以基于小樣本獲得可靠的估計量。實證分析表明，在基于評級標準的債券分組中，期限結構的貝葉斯分層模型估計量比通過非線性加權最小二乘的單曲線估計量更加符合經濟理論。而且貝葉斯分層模型在實踐應用中可以較為容易的實施，模型參數不需要進行過多的調整。因為MCMC算法對初始值和固定超參數的設定極不敏感，在不同的初值設定下，給定足夠大的迭代次數和合理的預燒期，總是可以獲得穩健的、合理的估計結果。

本文提出的利率期限結構的貝葉斯分層模型也可以用于擬合基于其他分類標準的債券的期限結構。實際上，除了信用評級之外，也有一些影響債券期限結構的其他因素：流動性，稅收和回收率等。將這些因素融期限結構估計的思路就是將它們也作為定義債券分類的標準。然而，以這些因素作為債券的分類標準，也會導致個別分組中的債券個數過小，利用本文的貝葉斯分層模型同樣可以解決這個問題。

貝葉斯分層模型也是一個靈活的模型，它并沒有被限定于僅僅估計特定類型的債券，比如該模型可以用于估計不同國家的債券之間的價差。我們可以將每一個國家看成是一類債券發行主體，然后聯合估計他們的期限結構，之后將兩個不同國家的估計曲線之間的差取為價差。此外，將企業或者政府債券與信用價差(企業債券和政府債券收益率之間的差)的估計進行結合，也可以利用貝葉斯分層模型方法。基于貝葉斯分層模型估計量的信用價差的計算可能會更加精確，因為在識別企業債券的潛在的期限結構方面，本文模型具有較好的績效。

總之，本文探究的期限結構估計的貝葉斯分層模型能夠在債券小樣本數據下，獲得期限結構更為精確的估計，它可以被廣泛的應用于各種期限結構的估計，而不會受到樣本容量的限制。

注釋

1. 數據來源：中國債券信息網和《2015年債券市場統計分析報告》，中央結算公司研發部，2016 年1月4日。