基于Logistic曲線擬合的全國電氣火災數據分析

艾 鵬，劉義祥，金 靜，許 潔，賈 南

(武警學院，河北 廊坊 065000)

●消防理論研究

基于Logistic曲線擬合的全國電氣火災數據分析

艾 鵬，劉義祥，金 靜，許 潔，賈 南

(武警學院，河北 廊坊 065000)

我國電氣火災發展形勢日益迅猛，給人民生產生活帶來巨大損失，因此研究電氣火災的發展規律具有現實意義。采用2004—2012年全國電氣火災數據，利用SPSS軟件比較不同曲線的擬合情況，最終確定Logistic邏輯增長模型，通過x2檢驗，判斷出曲線擬合優度，得出電氣火災預測公式，并粗略預測出2016年電氣火災發生比例。此模型的建立，可為消防部門了解電氣火災發展規律提供參考。

電氣火災；Logistic曲線；x2檢驗；擬合優度

0 引言

隨著我國經濟建設的大力發展，電能廣泛應用于人們生活生產活動中，然而電在造福人類的同時，由于電氣安全管理體系和法規建設的不完善，電氣操作和使用不當等諸多原因，導致電氣火災隱患及其發生率不斷增加，給國民經濟和人民生活造成巨大損失。據統計，我國電氣火災年均發生率達26%，年損失約占總損失的36%，而根據一些發達國家的資料顯示，英國每年電氣火災占總數的17%以下，而美國和日本更是低于10%。為降低電氣火災發生率，有必要著眼于火災數據分析和預測，為消防部門認識火災發展規律、判斷火災形勢、制定火災風險防范和控制計劃等提供重要依據[1]。

在我國，利用數據分析預測已經普遍應用于各行各業，其中利用數學模型預測火災發展也取得了許多成績，楚志勇[2]通過回歸分析的方法利用天津市歷年火災發生率數據建立回歸模型對未來的火災發生率進行了預測，鄭雙忠[3]通過等維灰色遞補GM(1，1)動態預測模型得出某市不同時段(共3個時段)火災發生率預測值，徐曉楠[4]以及陳俊達[5]等分別采用ARIMA法和指數平滑法兩種時間序列方法對火災發生率進行預測分析，預測結果與實際情況相比都較為精確。Logistic曲線是一種邏輯增長曲線，能較好地反映案例中的增長規律，在消防領域，Logistic主要用于火災風險評估及火險區域劃分等[6]，其大多是基于Logistic二項或多項回歸，構建概率模型，得出火災發生的可能性，但是Logistic曲線本身就具有邏輯增長的特點，可以通過曲線擬合預測火災起數，不過由于火災數據具有不完備性、隨機性等特點，通過Logistic曲線對火災數據進行擬合預測并不能應用于長時間段，其適合研究短時間段的火災發展規律。采用近10年全國電氣火災數據，比較各種預測模型，預測電氣火災的發展趨勢，希望能為今后的消防工作提供參考。

1 Logistics模型的預測方法

Logistic曲線方程是生物數學家P.F.Verhulst于1938年為了研究人口增長過程而導出的，其特點是在一定程度上穩定環境因素條件下，開始增長緩慢，而在以后的某一范圍內迅速增長，達到某限度后，增長又緩慢下來。曲線略呈拉長的“S”型[7]。其模型公式為：

Logistic曲線有3個關鍵點，用于研究曲線所代表的現實意義。求Logistic曲線方程的一階導數，可以得到Logistic增長或生長過程的速度函數：

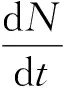
求Logistic生長速度函數的二階導數，令其等于0，得：

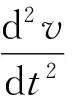
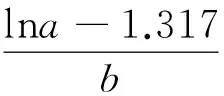
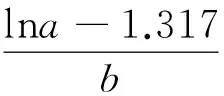
2 實例分析

2.1 數據預處理

數據來自中國消防年鑒(2004—2012年)，為消除屬性的量綱影響，進行去量綱化處理，求得每年的火災總數與電氣火災總數的比值作為處理后的數據進行統計分析，如表1所示。

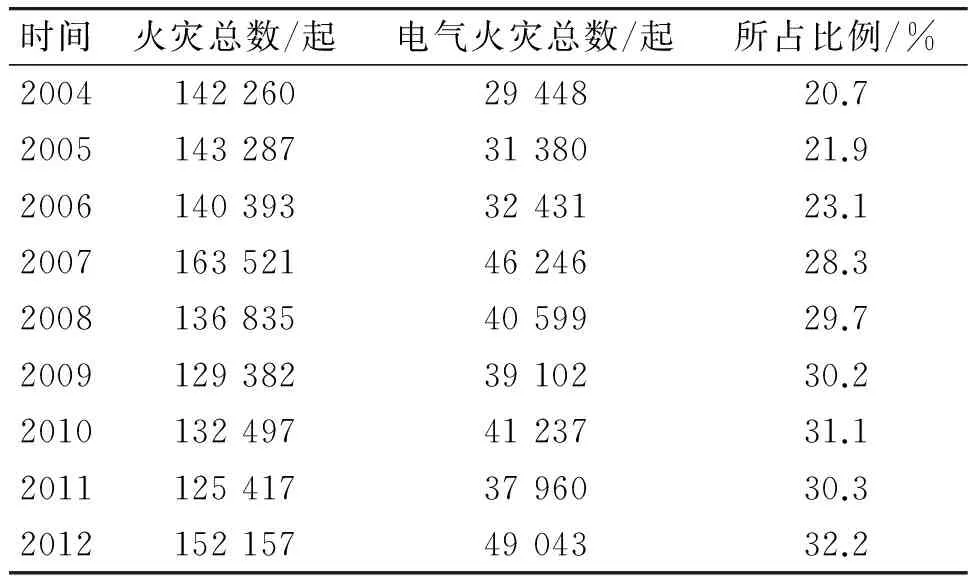
表1 全國電氣火災數據統計情況

2.2 比較不同曲線的擬合情況

為了找出最佳的擬合曲線，選定可決系數R2作為評價參數比較Logistic曲線與其他曲線，可決系數能夠反映曲線對樣本觀測值的擬合程度。通過SPSS中的曲線估計，得到一次、二次、三次、衰減指數擬合曲線的可決系數R2，如表2所示。

表2 不同擬合曲線的擬合優度

以全國電氣火災所占百分比為縱坐標，為了使數據簡單，便于計算，取橫坐標數值=當時年份-2000年，通過SPSS中的曲線估計得到圖1。根據可決系數值以及圖1所示，除直線外，其余曲線擬合都具有較高的精確度，但還需結合Logistic曲線的擬合情況進行比較。

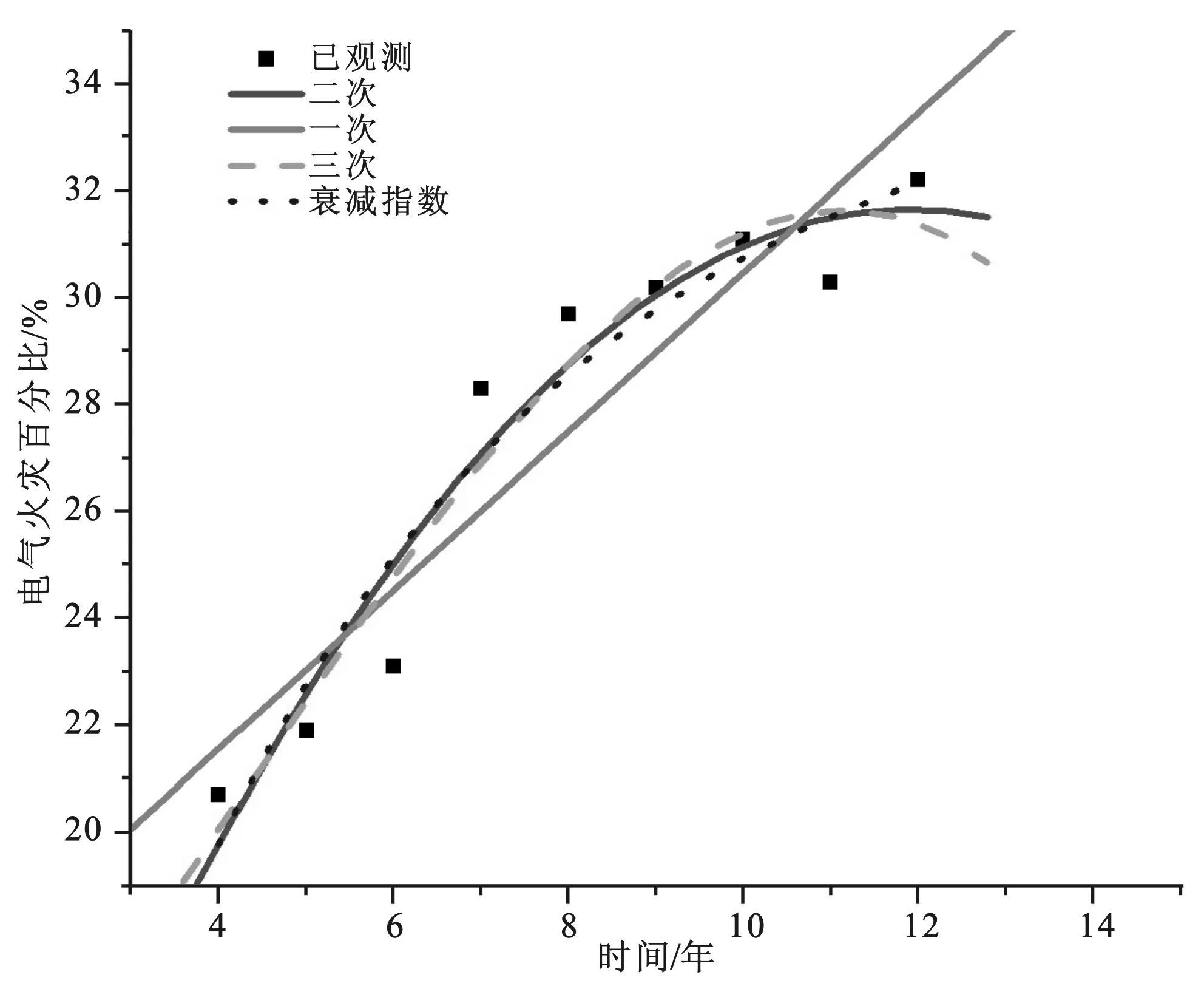
圖1 對全國電氣火災發生率擬合的曲線

2.3 Logistic曲線擬合

2.3.1 參數初始值估計

為了能夠使曲線的擬合效果更佳，決定探尋Logistic的擬合優度，主要采用SPSS軟件中的非線性擬合方法。首先應確定參數的初始值，以保證其后的迭代計算正常、迅速收斂，同時應避免參數初始值過小，計算時無法再收斂精確。由于Logistic曲線不可化為簡單的線性表達式，所以初始值的求解分為以下步驟進行：第一步求參數K，K值一般用三點法估計，公式[9]為：

式中，(t1，N1)、(t2，N2)、(t3，N3)分別表示實測數據序列的始點、中點、終點。其中K值采用三點法對其進行初始值的確定，這樣選取的點為2004、2008、2012年所對應的點，并將所對應的數據代入式(3)，解得K=32.80。

第二步估計參數a和b，由于式(1)具有非線性，利用其構造的模型為非線性模型，需轉化為線性模型后通過最小二乘法求解，式(1)經線性變化為：

z與t為線性回歸關系，利用Excel，由最小二乘法估計出參數a=e1.17，b=0.40[10]。

2.3.2 非線性擬合

非線性擬合的方法是不斷地將“參數估計值(參數的初始估計值)”代入“損失函數”求解，而“損失函數”采用的是“殘差平方和”最小，在迭代m次后，殘差平方和達到最小值，此時找到最優解，迭代終止。具體操作步驟：在SPSS中進入分析-回歸-非曲線擬合[11]，導入因變量電氣火災所占百分比，導入模型表達式K/(1+EXP(r-b*t))，其中r=lna，導入計算后的參數估計值K=32.80，b=0.40，r=1.17，保存預測值、殘差，選項中估計方法選擇序列二次編程，經過迭代計算后得出如表3所示的結果。由表中數據可知經過7次迭代計算后數據保持不變，最后的參數值K=33.049，r=1.099，b=0.374。同時通過SPSS得到Logistic的擬合曲線如圖2所示。

從圖2可以看出，Logistic模型對表1的電氣火災統計數據具有較好的擬合效果，根據SPSS得到的輸出結果，可決系數R2=0.939，具有非常高的擬合度，與圖1相比更能反映數據的邏輯增長特征；與表2中各個曲線的可決系數進行對比發現Logistic的數值更能接近1，因此Logistic曲線更能反映出數據特征，最后的曲線表達式為：

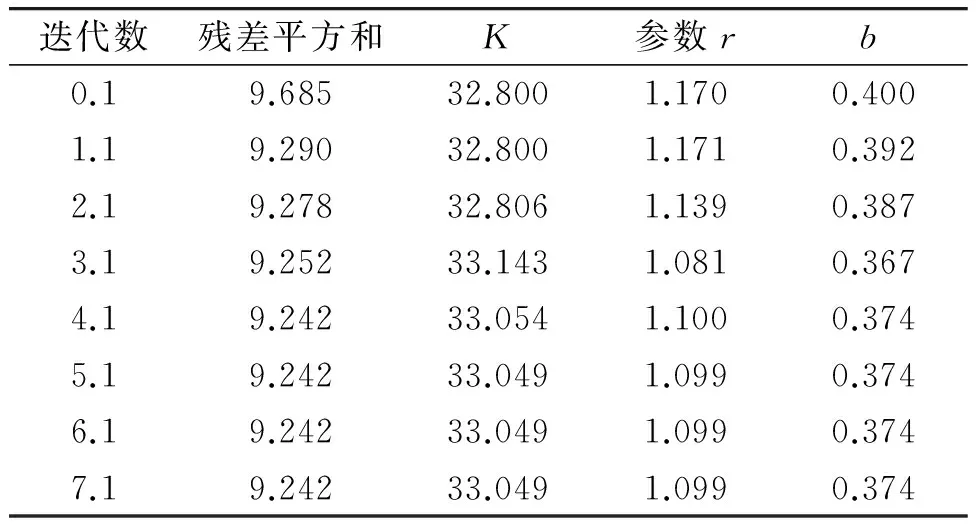
表3 迭代歷史記錄

圖2 用Logistic對全國電氣火災 發生率擬合的曲線

式(6)反映了全國電氣火災2004—2012年的邏輯增長情況，K值為33.049，代表電氣火災發生率所能達到的理論最高值，也是當前環境因素條件下的理論飽和值，當電氣火災發生率達到理論最高值時，之后的發展會因環境因素(社會經濟狀況、群眾防火安全意識等)的改變而出現明顯的改變。根據公式可以對未來的全國電氣火災發生率進行預測，經計算可以得出2013、2014、2015、2016年的電氣火災起數所占百分比預測值為32.29%、32.52%、32.68%、32.80%。

2.3.3 求取關鍵點

為研究實例的邏輯增長規律，分析曲線不同時段的增長特性，探求電氣火災發生率的現實情況，根據Logistic曲線的特點，求取式(6)的3個關鍵點，由式(2)可得Logistic曲線的3個關鍵點的橫坐標為t1=-0.59，t2=2.75，t3=6.53。因為文中數據是取自2004—2012年的，是基于某一時段的數據分析，時間作為因變量，且數據自變量包含的時間范圍較短，所以Logistic曲線會在x軸上有偏移，出現t值為負的情況，表示1999年之前的情況，這里不做分析。根據計算出的3個關鍵點可知，全國電氣火災發生率快增期為2004—2007年，緩增期為2007年—∞。

2.3.4x2檢驗

由于Logistic曲線回歸方程除含有回歸參數a和b，還含有常量K，為了更精準地驗證曲線的擬合優度，利用實際值和預測值，運用x2測驗，確定曲線的擬合優度，以驗證公式的合理性[8]。

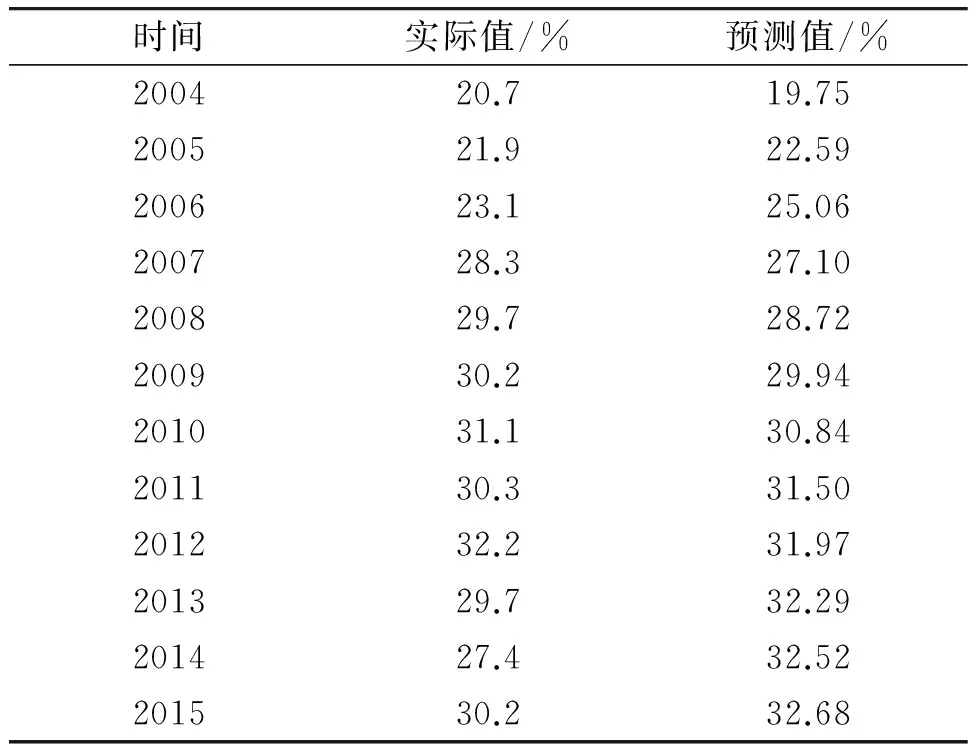
表4 全國電氣火災所占比例的實際值與預測值

3 結論

通過R2值的比較與x2檢驗發現Logistic曲線的擬合效果更好，因此針對實例確定最終的推導公式(6)，并對2013、2014、2015、2016年的火災進行預測，得出結果為2013、2014、2015作為檢驗年份預測值為32.29%、32.52%、32.68%，與實際值29.7%、27.4%、30.2%基本相符，2016的電氣火災發生比率預測值為32.80%。分析我國電氣火災發生率的增長規律發現我國電氣火災仍處于持續高發狀態，2004—2007年是我國電氣火災的高速增長期，特點為電氣火災發生基數不大，但發生比率在逐年高速增長。2007年開始是我國電氣火災的緩增期，特點為電氣火災發生比率仍逐年增加，但增加的速度明顯減小，電氣火災的發展逐漸進入穩定期。

[1] 蘭麗娜.我國電氣火災發展的特點分析及其綜合防治對策研究[J].科技風,2011(8):251-252.

[2] 楚志勇.基于回歸分析方法的城市火災預測:以天津市為例[J].安全與環境工程,2011,18(3):90-92.

[3] 鄭雙忠.基于灰色系統理論的城市火災預測分析[J].數學的實踐與認識,2005,35(1):72-76.

[4] 徐曉楠,張曉珺,施照成.基于北京市火災統計數據的時間序列分析[J].安全與環境學報，2014,14(1):73-77.

[5] 陳俊達,李曉宏,李佳樂,等.基于時間序列分析的火災分析與預測[J].科學之友,2011(11):42-43.

[6] 王衛國,潘竟虎,李俊峰.基于空間Logistic的山西省火災風險評價與火險區劃[J].草業科學,2016,33(4):635-644.

[7] 胡喜生,范海蘭,宋萍,等.改進Logistic模型在城市人口預測中的應用[J].北華大學學報(自然)，2008,9(4):370-373.

[8] 崔黨群.Logistic曲線方程的解析與擬合優度測驗[J].數理統計與管理,2005,24(1):112-115.

[9] 殷祚云.Logistic曲線擬合方法研究[J].數理統計與管理,2002,21(1):41-46.

[10] 張潤蓮,蘇國強,楊建華,等.基于Logistic模型的火災損失研究文獻分析[J].內江科技,2013,34(11):107-108.

[11] 董江水.應用SPSS軟件擬合Logistic曲線研究[J].金陵科技學院學報,2007,23(1):21-24.

(責任編輯馬龍)

AnalysisofNationalElectricFireDataBasedonLogisticCurveFitting

AI Peng, LIU Yixiang, JIN Jing, XU Jie, JIA Nan

(TheArmedPoliceAcademy,Langfang,HebeiProvince065000,China)

The number of China’s electrical fire is increasing rapidly, bringing great losses to people’s production and life, so to study the law of electrical fire occurrence is of great significance. In this paper, the SPSS software is used to compare the fitting of different curves based on the data of national electrical fires from 2004 to 2012. Finally, a Logistic logic growth model is determined. The goodness of curve fitting is obtained by Chi-square test, and a prediction formula of electrical fires is obtained, which can roughly forecast the proportion of electrical fires in 2016. This model provides a reference for the fire department to understand the law of electrical fire occurrence.

electrical fire; Logistic curve; Chi-square test; goodness of fitting

2017-04-10

河北省統計科學研究計劃項目“大數據背景下城市火災預測與可視化研究”(2016HY11)階段性成果； 河北省科技計劃項目“面向大數據的城市火災預測關鍵技術研究”(16215416)階段性成果

艾鵬(1993— )，男，遼寧錦州人，武警學院在讀碩士研究生； 劉義祥(1970— )，男，河北南皮人，教授； 金靜(1986— )，女，安徽蕭縣人，講師，博士； 許潔(1983— )，女，河北廊坊人，講師； 賈南(1987— )，男，河北廊坊人，講師。

D631.6

A

1008-2077(2017)10-0005-04