基于局部特征匹配的網格去噪算法

產海林，曹 璨

(1.中國科學技術大學 數學科學學院，安徽 合肥 230026； 2.中國科學技術大學 信息科學技術學院，安徽 合肥 230026)

基于局部特征匹配的網格去噪算法

產海林1，曹 璨2

(1.中國科學技術大學 數學科學學院，安徽 合肥230026；2.中國科學技術大學 信息科學技術學院，安徽 合肥230026)

由于三維掃描設備精度不足以及各類人為因素的影響，掃描獲取的三維模型不可避免地包含了噪聲信息。如何有效地去除掃描模型中的噪聲一直是一個經典熱門問題。文中提出了一個數據驅動的算法，通過分析已有的噪聲模型和對應原始模型數據，建立噪聲模型局部幾何特征與原始模型法向量之間的數據映射關系，再利用此信息局部特征匹配得到去噪后網格。實驗結果表明，該方法可以有效地對網格進行去噪，在去除噪聲的同時，可以很好地保持網格的特征結構。

網格去噪；局部特征匹配；數據驅動；引導法向濾波

0 引言

三維掃描儀和深度相機的流行大大簡化了三維幾何建模的過程，使得人們可以很容易地得到各種真實世界物體的三維形狀數據。但與藝術家手動生成的模型不同的是，掃描得到的模型往往包含各種噪聲。在數字幾何處理中，去除掃描模型中的噪聲一直是一個經典熱門的問題。本文主要探討了對三角網格的去噪問題，還有一些工作[1]直接考慮了掃描儀獲取的點云數據的去噪問題。

網格去噪的本質是，從測量數據M*=M+ε中去除噪聲ε，得到真實原始網格M。原始網格M和噪聲ε均未知，這本身就是個病態問題。由于噪聲和網格的尖銳邊角特征都是高頻的，這導致很難將它們分離開，因而網格去噪問題面臨的最大挑戰是如何在去除噪聲的同時可以保持網格的原始特征。

文獻[2-4]通過一個低通濾波器來去除高頻噪聲，由于各向同性，這些方法不能區分噪聲和網格特征，在去除噪聲的同時也會丟失網格模型的尖銳特征。Jones等人[5]、Fleishman等人[6]提出了各向異性算法，將圖像去噪中的雙邊濾波擴展到了網格中，根據三維網格的幾何特征來改變雙邊濾波的權重，達到保持特征的目的。文獻[7-12]提出了兩步走的方法，首先將濾波器作用到法向量域，調整法向量，再利用調整后的法向量信息來更新頂點坐標。雖然以上基于濾波的方法對各類噪聲模型一定程度上可以有效地去噪，但其需要用戶大量的手動調整參數工作來得到一個較合理的結果。

基于優化的方法，通過構建求解優化問題得到一個滿足一系列約束同時與輸入近似的模型。文獻[13]使用了L0優化，要求潛在原始模型是分片光滑的。文獻[14]使用了壓縮感知方法，將模型與噪聲分離開，其要求噪聲是獨立同分布的。這些方法對于滿足條件的特定幾何特征或噪聲類型可以生成好的結果，但對于其他不符合條件的特征和噪聲類型就很難處理。此外，優化過程往往都很慢。

文獻[15]采用了數據驅動的方法，利用大量的帶噪聲模型和原始模型來做學習回歸，建立了兩者間的回歸模型，達到去除噪聲的目的。數據驅動方法的好處在于無需人工調整參數，且不對模型幾何特征和噪聲類型做特殊限定。但文獻[15]采用了單隱層的神經網絡對所有數據進行全局擬合，得到回歸函數，限于神經網絡的表達能力，全局方法容易產生過擬合以及存在受無關信息干擾等問題，其去噪效果依然存在著一定缺陷。

為此，本文在數據驅動方法的基礎上，采用了局部特征匹配的方法。首先，利用已有模型信息，構建數據庫，存儲帶噪聲模型的局部幾何特征和原始模型面法向間的映射關系；然后在對新輸入模型做去噪時，利用數據庫中最相近的信息構造局部擬合函數，得到校準后的網格面法向量；最后，根據校準面法向量信息來更新頂點坐標，得到去噪后模型。

1 網格幾何特征的計算

1.1雙邊濾波與聯合濾波

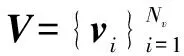
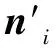
(1)

式中Λ(·)為向量單位化算子。Ws、Wr為非負單調遞減核函數，分別度量了網格在兩面片fi、fj上的空間相似度和法向域相似度。核函數通常使用高斯函數Wσ=exp(-x2/ (2σ2))，Ws、Wr中的標準差σ分別記做σs、σr。

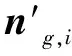
(2)

式中gi、gj分別為面fi、fj上的引導法向量，引導法向量的計算可以簡單采用鄰域加權平均的策略：

(3)

1.2幾何特征計算

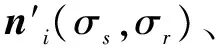
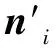
(4)

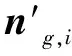
(5)

本文方法也采用了類似的思想，不同的是，本文在計算聯合濾波時采用了更加精細的策略，結合了文獻[16]中計算引導信號G的方法。一般網格模型都是分片光滑的，由尖銳的邊分成不同的光滑區域。式(3)中，在尖銳的邊附近直接簡單地采用一鄰域加權平均作為引導法向量是不合理的，因為跨越尖銳邊的兩個區域的面法向量之間是有較大差異的。在計算式(3)中鄰域N(fi)時就應當僅僅考慮面fi所在光滑區域的面片。

對于鄰域的選取，考慮鄰域N(fi)的可能候選Nk(fi)，計算其面法向量一致性評估函數H(Nk)，選擇評估函數H(Nk)最小的對應候選鄰域N*(fi)來計算引導濾波。評估函數H(Nk)定義如下：

H(Nk)=Φ(Nk)·R(Nk)

(6)

式中Φ(Nk)、R(Nk)分別為區域Nk上任兩個面法向量的最大差異和邊的最大差異，因而H(Nk)越小則反映了區域Nk上的面法向量越一致。

圖1為式(3)簡單選取鄰域以及與本文方法的對比，從左到右依次為噪聲模型、原始模型、簡單選取鄰域時法向差異、本文方法法向差異，顏色表示計算得到的引導法向量與原始法向量間的差異，顏色越接近藍色表示差異越小。可以看到，相比式(3)簡單選取方法，本文的方法得到的引導法向量更加接近真實數據，為后續的去噪過程提供了一個更加魯棒準確的面法向信息。

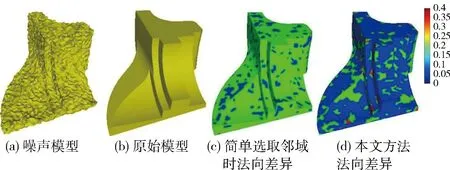
圖1 不同引導法向的對比

綜上，對于網格M上面fi的幾何特征描述子Sg,i的計算步驟如下：

(1)對于面fi的每個候選鄰域Nk(fi)，根據式(6)計算評估函數H(Nk)，選擇評估函數H(Nk)最小的鄰域作為最佳鄰域N*(fi)；

(2)計算面fi在鄰域N*(fi)上的高斯濾波作為引導法向gi；

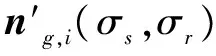
(4)將不同參數對(σs,σr)的聯合法向濾波聯立起來，即得到面fi的幾何特征描述子。

2 局部特征擬合的網格去噪算法

對于給定的一帶噪聲網格，本文目的是得到去噪之后的潛在原始模型。本文算法可以分為以下三個步驟：(1)對已有模型數據做處理，計算帶噪聲模型面片上的局部幾何特征和原始模型的面法向量，并建立數據庫存儲兩者間的對應關系；(2)對于輸入的帶噪聲網格，計算其面片上的局部幾何特征，在數據庫中查找最相近的信息來局部擬合，得到校準后的面法向量；(3)基于校準后的面法向量更新頂點坐標，得到去噪模型。

2.1數據預處理

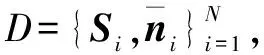
2.2局部特征匹配

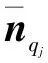
(7)

高維流形的每個局部都可以由線性空間去逼近[17]，此處本文使用了局部線性插值來得到校準法向量。 權重wj反映了面fqi與面fp的關聯程度(wj越大表示面fqi與面fp的關聯程度越大)，其通過求解以下優化問題得到：

(8)

此問題可以轉化為求解方程(ZT*Z)·W=1，式中W=(w1,…,wk)T,Z=(Sq1-Sp,…,Sqk-Sp)。

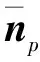
圖2展示了本文局部擬合方法和文獻[15]的全局方法的去噪效果對比，可以看到本文方法去除噪聲效果更好，而全局擬合方法依然殘留了一些高頻噪聲信息。

圖2 局部與全局擬合方法的對比結果

2.3頂點更新

通過2.2節可以得到帶噪聲模型校準后的面法向量，然后基于校準后的面法向量更新頂點得到去噪模型。類似于很多基于法向量濾波的網格去噪方法[10-11,16]，本文采用以下策略進行頂點更新：

(9)

式中，vi為網格頂點，nj為網格面法向量，cj為面的中心，Fi為頂點vi的一鄰域面。

與文獻[11]的兩步走方法相類似，本文同樣迭代地進行面法向量更新和頂點更新兩個步驟，直到得到一個最佳的結果。

3 實驗結果與分析

本節中，將展示本文方法的效果圖，并與其他去噪方法的效果做對比。本文在操作系統為Windows 10、處理主頻為2.8 GHz、系統內存16 GB的PC上，采用Microsoft Visual C+ + 2013軟件平臺實現了本文的算法。網格數據集本文采用了文獻[15]中的數據，主要分為兩類，一類為人工制造的各種幾何模型(CAD模型、光滑模型等)，對其加上不同類型的噪聲得到對應的噪聲模型；另一類為實際掃描采集的帶噪聲模型，并與人工生成的無噪聲模型做好了匹配對應。對于人工制造的模型，本文中主要測試了高斯噪聲，對每個原始模型都加上了三種不同程度的高斯噪聲。對于掃描模型，本文主要考慮了Kinect、Kinect Fusion采集的模型。

在本文實驗中，式(4)、式(5)中的參數選取σs為l、2l、4l，其中l為網格的平均邊長，σr為0.1、0.2、0.35、0.5、10，則參數對(σs,σr)一共有15種組合。式(7)中k為查找最近鄰的個數，實驗中取值為5。

網格去噪的目的是將帶噪聲模型最大程度地恢復至原始模型，衡量去噪性能的指標就是經去噪得到的三維模型與原始網格的接近程度，本文采用去噪模型與原始模型的面法向量的平均角度差異作為評判標準。

本文選擇了目前優秀的去噪算法：雙邊濾波[6]、雙邊法向濾波[11]、指導法向濾波[16]、L0優化[13]、級聯法向回歸[15]，將它們與本文方法進行對比。

在圖3中，展示了本文方法與其他方法的對比，對人為加高斯噪聲的模型進行去噪。一方面，本文方法可以很好地去除噪聲，而雙邊濾波、雙邊法向濾波、級聯法向回歸等方法都依然殘留有噪聲，去除效果不佳；另一方面，相比其他方法，本文方法可以保留更多的細節信息，而指導法向濾波、L0優化等方法往往將這些細節平滑或尖銳化。同時從客觀數值上看，本文方法得到的去噪模型與原始三維網格更為相近，去噪效果最優。圖3中，法相平均角度差異分別為：第一行：13.23、8.23、8.08、14.93、8.04、7.89；第二行：7.45、5.46、6.13、7.34、5.19、5.02。

圖3 不同去噪方法的對比結果

本文方法也可以很好地應用到掃描模型上，例如圖4，對于Kinect、Kinect Fusion掃描的模型，本文方法在去除噪聲和保持特征方面依然效果很好。圖4中，第一行為Kinect模型，第二行為Kinect Fusion模型。法相平均角度差異分別為：第一行：16.03、16.276、12.38、11.26、8.72、7.57；第二行：10.72,、9.39、7.92、7.82、7.74、7.38。

圖2、圖5也展示了本文方法和級聯法向回歸方法的對比。在這些圖片中，本文局部擬合方法均比文獻[15]的全局擬合方法去噪效果更好。

圖4 不同掃描模型下不同去噪方法的比較

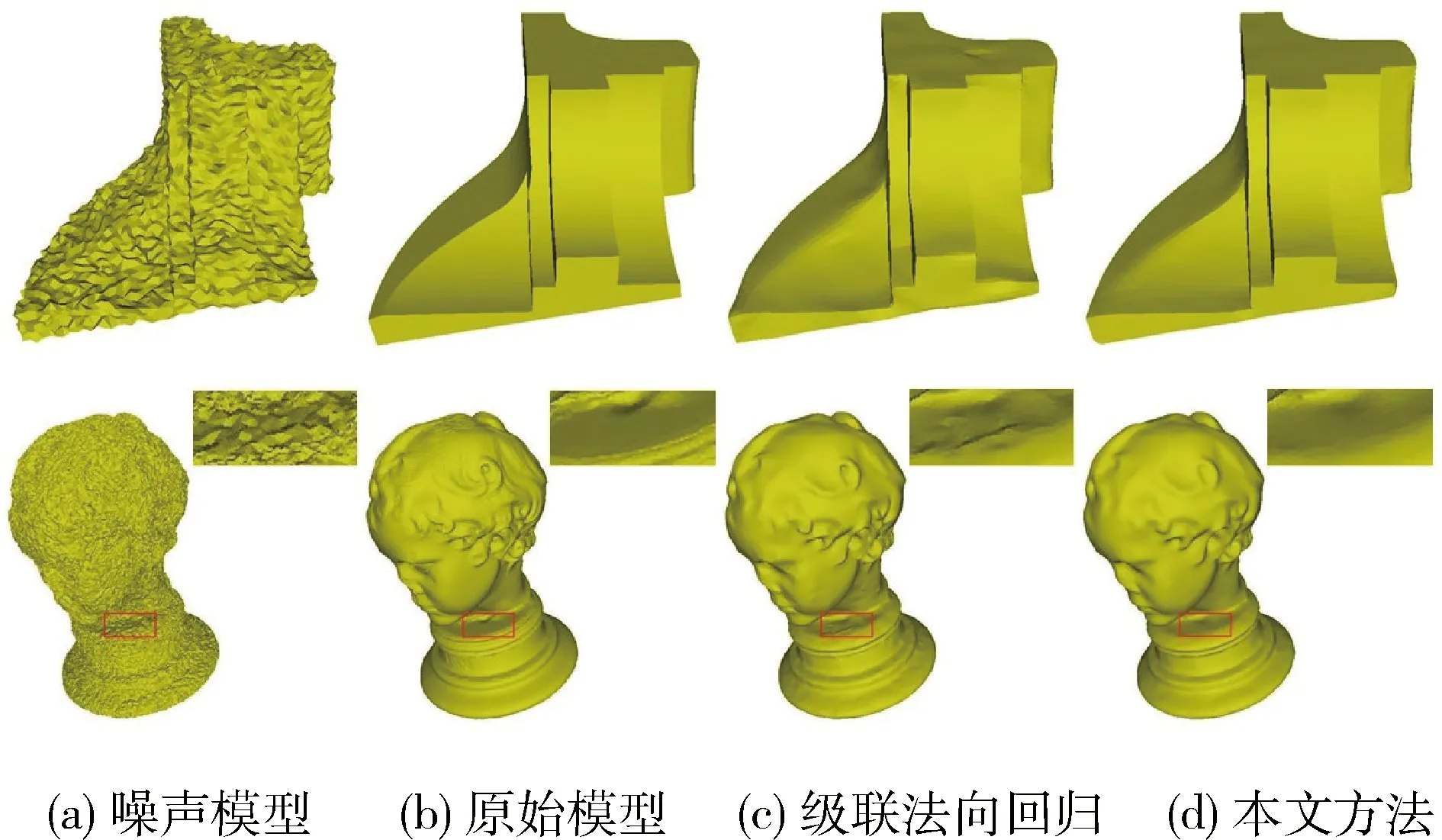
圖5 局部與全局擬合方法的對比結果

4 總結與展望

本文通過對帶噪聲模型與原始模型信息的充分分析，提出了一種新的局部特征擬合的網格去噪方法。實驗表明，對于人為加噪聲模型和掃描模型，本文方法在去除噪聲和保持網格特征結構方面都效果很好。

在后續的研究中，將嘗試采用端到端的深度學習方法(end-to-end deep learning)，將網格的幾何特征定義與網格去噪過程結合起來，利用深度神經網絡的強大表達能力來得到一個優異結果。

[1] 郝慧麗，劉先勇.含噪點云預處理技術研究[J].微型機與應用，2012，31(12): 68-70.

[2] TAUBIN G.A signal processing approach to fair surface design[C].Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques.ACM，1995: 351-358.

[3] DESBRUN M，MEYER M，SCHR?DER P，et al.Implicit fairing of irregular meshes using diffusion and curvature flow[C].Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques.ACM，1999: 317-324.

[4] OHTAKE Y，BELYAEV A，BOGAEVSKI I.Mesh regularization and adaptive smoothing[J].Computer-Aided Design，2001，33(11): 789-800.

[5] JONES T R，DURAND F，DESBRUN M.Non-iterative，feature-preserving mesh smoothing[J].ACM Transactions on Graphics，2003，22(3): 943-949.

[6] FLEISHMAN S，DRORI I，COHEN-OR D.Bilateral mesh denoising[J].ACM Transactions on Graphics, 2003，22(3): 950-953.

[7] YAGOU H，OHTAKE Y，BELYAEV A.Mesh smoothing via mean and median filtering applied to face normals[C].Proceedings of Geometric Modeling and Processing，2002.IEEE，2002: 124-131.

[8] YAGOU H，OHTAKE Y，BELYAEV A G.Mesh denoising via iterative alpha-trimming and nonlinear diffusion of normals with automatic thresholding[C].Computer Graphics International, 2003: 28-34.

[9] SHEN Y，BARNER K E.Fuzzy vector median-based surface smoothing[J].IEEE Transactions on Visualization and Computer Graphics，2004，10(3): 252-265.

[10] SUN X，ROSIN P，MARTIN R，et al.Fast and effective feature-preserving mesh denoising[J].IEEE Transactions on Visualization and Computer Graphics，2007，13(5): 925-938.

[11] ZHENG Y，FU H，AU O K C，et al.Bilateral normal filtering for mesh denoising[J].IEEE Transactions on Visualization and Computer Graphics，2011，17(10): 1521-1530.

[12] WEI M，YU J，PANG W M，et al.Bi-normal filtering for mesh denoising[J].IEEE Transactions on Visualization and Computer Graphics，2015，21(1): 43-55.

[13] HE L，SCHAEFER S.Mesh denoising via L 0 minimization[J].ACM Transactions on Graphics (TOG)，2013，32(4): 64.

[14] WANG R，YANG Z，LIU L，et al.Decoupling noise and features via weighted1-analysis compressed sensing[J].ACM Transactions on Graphics (TOG)，2014，33(2): 18.

[15] WANG P S，LIU Y，TONG X.Mesh denoising via cascaded normal regression[J].ACM Transactions on Graphics (TOG)，2016，35(6): 232.

[16] ZHANG W，DENG B，ZHANG J，et al.Guided mesh normal filtering[J].Computer Graphics Forum, 2015，34(7): 23-34.

[17] ROWEIS S T，SAUL L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290(5500): 2323-2326.

Mesh denoising based on local feature matching

Chan Hailin1, Cao Can2

(1.School of Mathematical Sciences，University of Science and Technology of China，Hefei 230026，China;2.School of Information Science and Technology，University of Science and Technology of China，Hefei 230026，China)

Limited by the inaccuracy of three-dimensional scanners and the various human factors，the three-dimensional models acquired by scanning contain noise inevitably.How to remove the noise on the acquisition models effectively is a hot classic topic.In this paper, we present a data-driven algorithm.Through analyzing the existing noisy mesh and their corresponding ground-truth mesh，we establish the correspondence between the local geometric features of the noisy mesh and the facet normals of the ground-truth mesh，which is used to guide the mesh denoising.The results of experiments verify that the method can effectively denoise the mesh，and is significantly better in reducing noisy and preserving the features of the models.

mesh denoising; local feature matching; data-driven; guided normal filter

TP391.41

A

10.19358/j.issn.1674-7720.2017.21.004

產海林，曹璨.基于局部特征匹配的網格去噪算法J.微型機與應用，2017,36(21)：11-14，18.

2017-05-11)

產海林(1992-)，男，碩士，主要研究方向：數字幾何處理、機器學習。

曹璨(1992-)，女，碩士，主要研究方向：數據挖掘。