電推力器中復雜電場求解的超松弛并行算法
,,*,,,,
1.大連理工大學 工業裝備結構分析國家重點實驗室,大連 116024 2.中國空間技術研究院 通信衛星事業部,北京 100094
電推力器中復雜電場求解的超松弛并行算法
韓亞杰1,夏廣慶1,*,吳秋云1,陳留偉1,周念東1,溫正2
1.大連理工大學 工業裝備結構分析國家重點實驗室,大連 116024 2.中國空間技術研究院 通信衛星事業部,北京 100094
目前,電推力器中復雜電場的三維泊松方程求解仍存在速度偏慢、并行性欠佳等缺陷。通過分解三維求解區域,針對復雜電場提出一種超松弛并行(P-SOR)迭代算法。將求解區域劃分為多個子塊,利用超松弛迭代格式構造出若干分組顯式格式,分別給出不同迭代步數下的求解方程以進行并行計算。通過數值模擬,計算時間至少縮短一半以上,該P-SOR方法較傳統迭代格式在快速性方面取得較大進展,對電推進領域的數值仿真研究起到促進作用。
電推力器;泊松方程;超松弛迭代;并行算法
泊松方程是等離子體物理、靜電學中常見的偏微分方程,其應用范圍較廣,特別是在電推力器中復雜電場的求解方面。現階段,大規模的科學工程計算對于速度快、容量大的并行機和有效的數值并行算法均有較大的需求,特別是在航天領域。基于粒子云網格(Particle In Cell,PIC)方法[1]的數值計算,通過泊松方程來求解復雜電場,在電帆仿真計算[2],霍爾推力器的相關研究[3]等領域均有廣泛應用。但由于三維模型求解速度很慢,諸多研究人員針對模型做出簡化,如采用二維模型、二維軸對稱模型[4-5]等,其精確度難免會下降。所以本文針對加快三維泊松方程的求解速度開展研究。
國內外已有一些專家學者在該領域進行了探索。現在通用的并行模塊大多采用Jacobi迭代[6],其具有顯性的并行性。但是對于求解速度,超松弛迭代等方法則要遠遠高于Jacobi格式,也有很多學者對其進行研究。例如,文獻[7]提出一種針對點的SOR并行方法,但是在擴展性方面存在較大的劣勢,不利于大規模應用。文獻[8]提出一種新型的、應用于統一計算架構(CUDA)的并行算法,利用GPU的硬件特性對泊松方程的求解進行加速。文獻[9]提出一種塊SOR理論,改進其求解速度,并對收斂性做出研究。文獻[10]提出一種基于Richardson外推法的三維泊松方程差分格式,具有使用網格基架點少、精度高、穩定性好等優點。但是對于三維泊松方程的多線程并行計算的研究仍較為欠缺。
本文提出一種基于三維泊松方程的并行計算理論,適用于OpenMP并行模塊[11],并采用電場結構較為復雜的柱形和球形慣性靜電約束電推力器[12](Inertial Electrostatic Confinement Thruster,IECT)為模型進行相應的數值模擬,通過對比不同迭代方法的求解時間,對其快速性進行驗證。
1 泊松問題及分組顯式格式
1.1泊松問題
考慮在長方體區域Ω上的三維泊松方程,
式中:Ω=[0≤x≤L]×[0≤y≤M]×[0≤z≤N]為求解區域,?Ω為Ω的邊界;u(x,y,z)為待求函數,f(x,y,z)和g(x,y,z)為已知光滑函數。
對于泊松方程內部點的逼近方法有很多,這里采用最為常見的七點差分格式[13]:
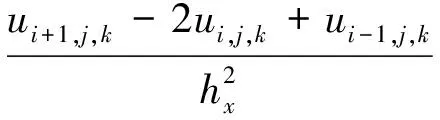
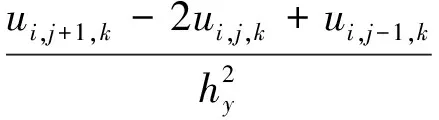
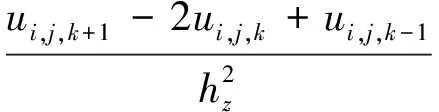
對區域Ω進行一致剖分,空間步長取為h,在x,y和z方向分別為(l+1)h=L,(m+1)h=M與(n+1)h=N,則定義xi=ih,i=0,1,…,l+1;yj=jh,j=0,1,…,m+1;zk=kh,k=0,1,…,n+1,記(xi,yj,zk)為(i,j,k),則有:
SOR方法很符合求解此類問題,但它沒有明顯的并行性,所以這里將給出一個新的并行SOR迭代算法,簡稱為P-SOR。根據對二維并行迭代格式的研究[14],推導出基于三維泊松方程的8個基本SOR迭代格式:
式中:ω為松弛因子。
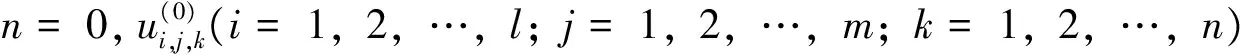
1.2 分組顯式格式
首先,考慮求解域中相鄰8個網格點的數值解,如圖1所示,聯立A1~A8可形成(8×8)階方程組,采用分組顯式的思想,即可得到求解域節點(i,j,k),(i,j+1,k),(i+1,j,k),(i+1,j+1,k),(i,j,k+1),(i,j+1,k+1),(i+1,j,k+1),(i+1,j+1,k+1)處的數值解公式。
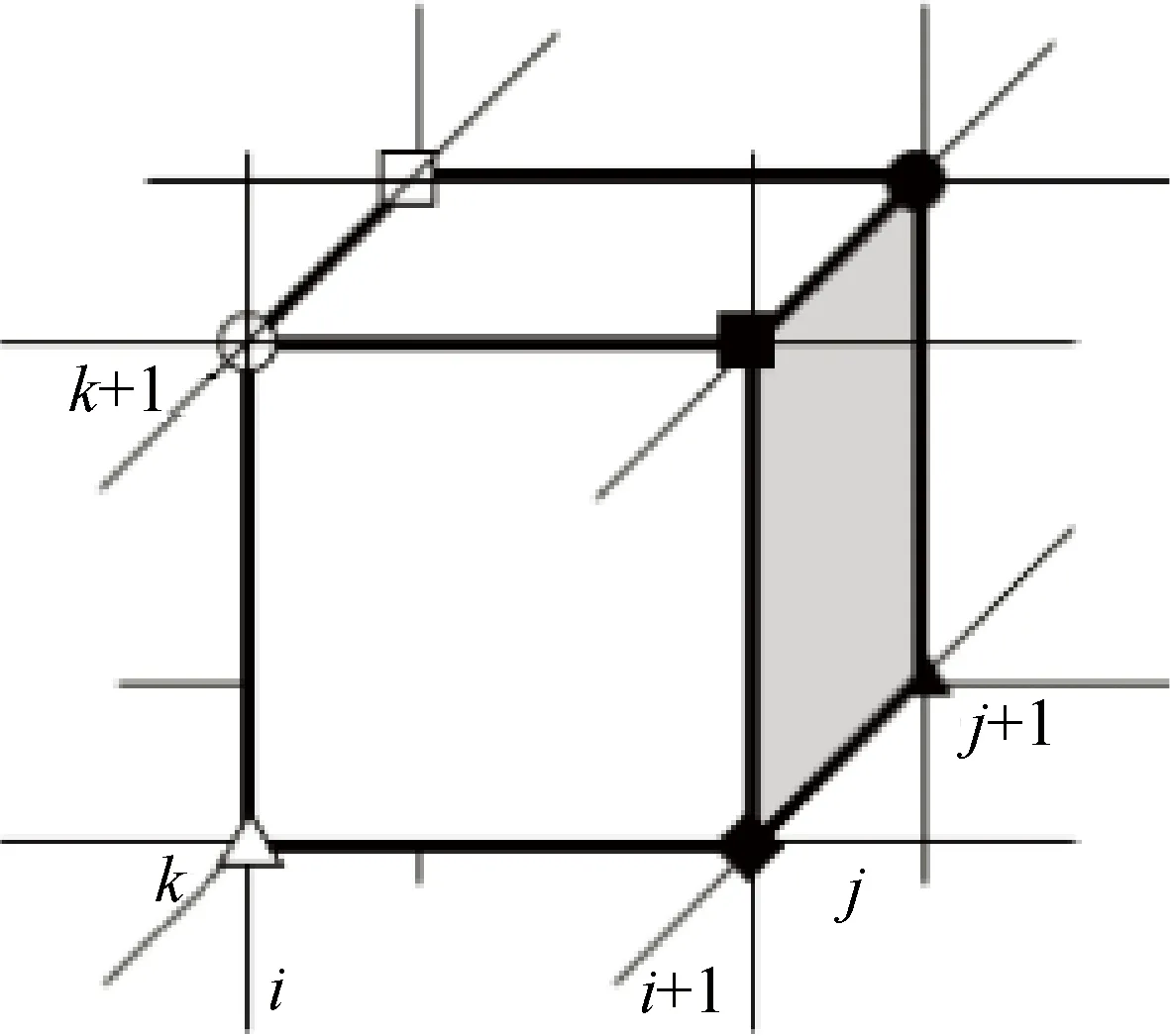
圖1 中間點迭代示意Fig.1 Schematic diagram of intermediate point iteration
令
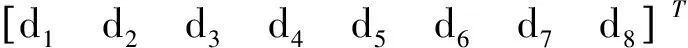
其中
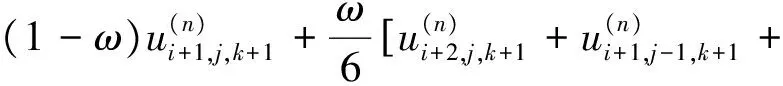
即可求出方程組:
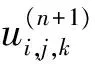
f2d5+4ω2d6+4ω2d7+2ω3d8)
4ω2d5+f2d6+2ω3d7+4ω2d8)
4ω2d5+2ω3d6+f2d7+4ω2d8)
2ω3d5+4ω2d6+4ω2d7+f2d8)
f1d5+f2d6+f2d7+4ω2d8)
f2d5+f1d6+4ω2d7+f2d8)
f2d5+4ω2d6+f1d7+f2d8)
4ω2d5+f2d6+f2d7+f1d8)
式中:
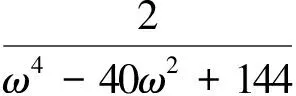
f1=-14ω2+72,f2=-ω3+12ω
類似地,利用分組顯式基于“四點一組”的思想可構造其他6個新的格式。
利用格式A1,A3,A5,A7求解內邊界點(i,j0,k),(i+1,j0,k),(i,j0,k+1)和(i+1,j0,k+1),j0=j+2,j+3,…,m可得格式A10:

用類似的方法即可求出另外5個迭代格式A11~A15,其基本表現形式相同,這里不再詳述。
特別地,當f(i,j,k)=0時,該泊松方程即退化為拉普拉斯方程。對于超松弛系數ω的選取,可以參考文獻[15]。
2 P-SOR算法流程
2.1區域分解
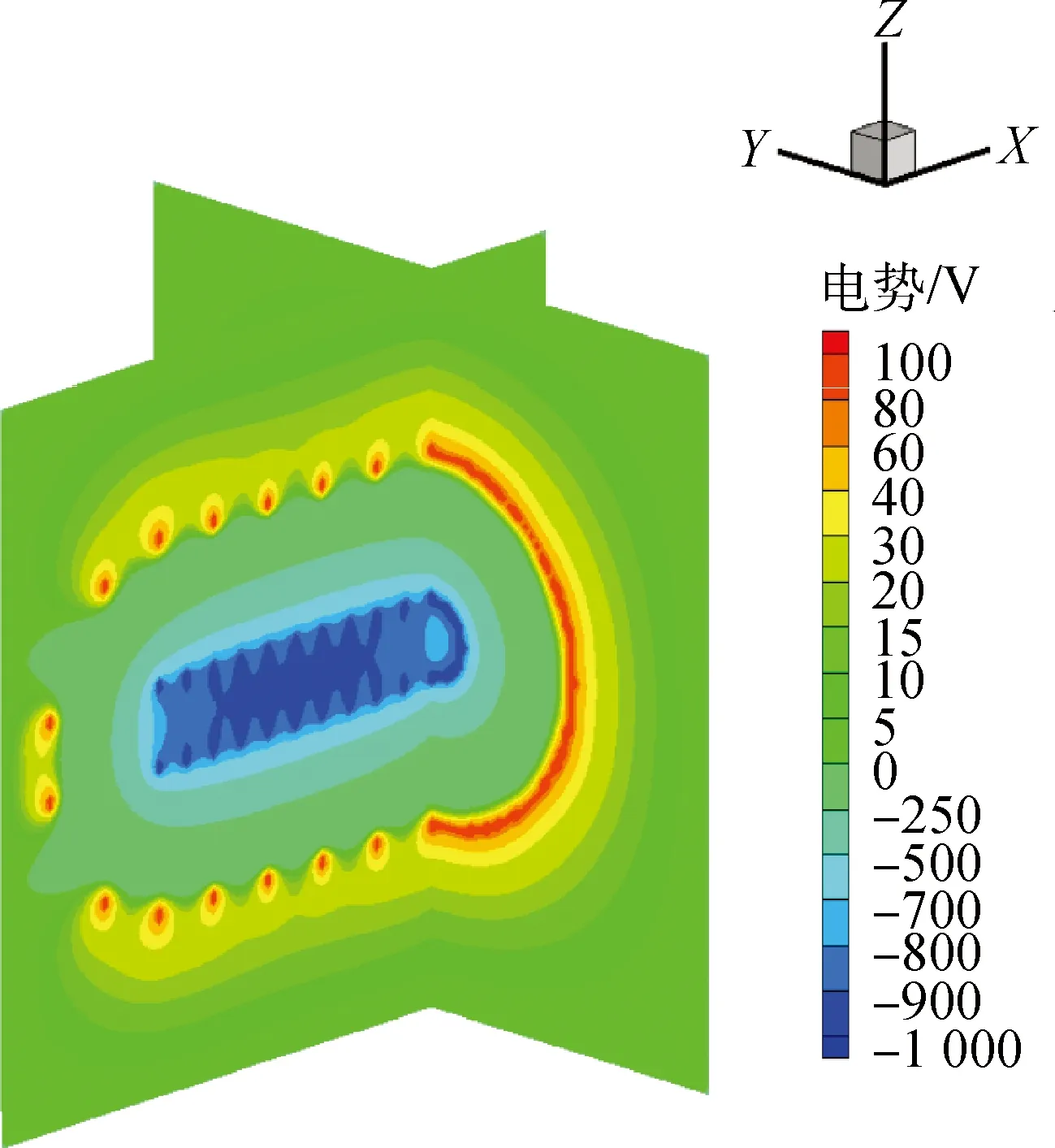
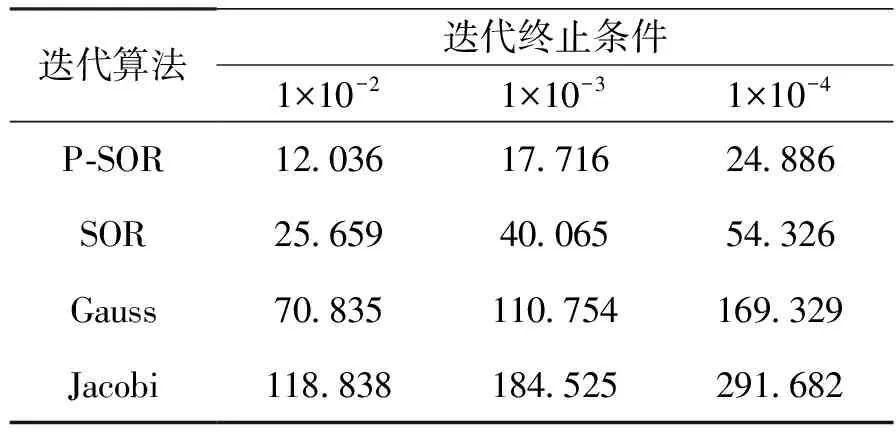
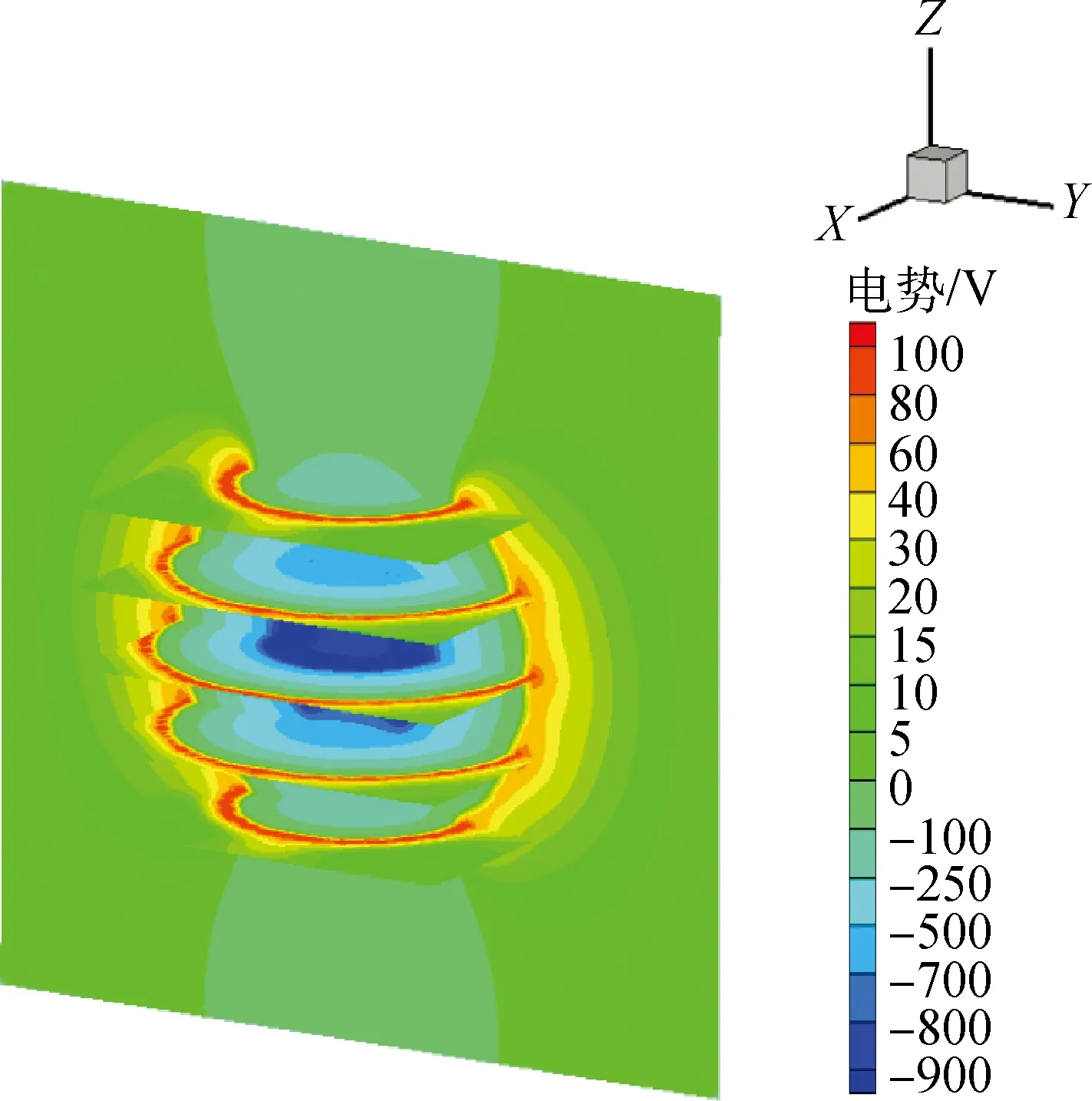
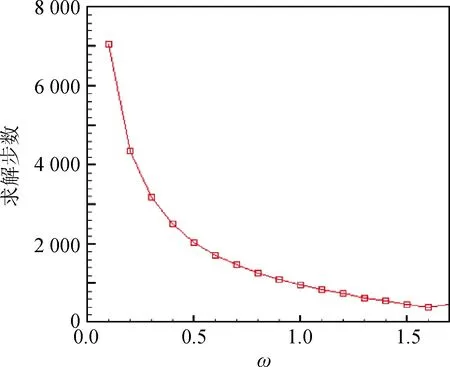
首先,將區域Ω分解為若干子域,這里以8個非重疊子域為例(其他以此類推),如圖2所示,用6個網格平面(i=p,p+1,j=q,q+1,k=r,r+1)將求解區域劃分的8個子域,其中p,q,r為任意正整數,0 圖2 求解域網格劃分Fig.2 Meshing partitions in the calculation domain 2.2 迭代算法 顯然,在求解過程中對于相同的區域不能使用同一種迭代格式,這樣會造成不同時間步的電勢值無法更新迭代。所以,對于奇數次迭代和偶數次迭代,采用不同的迭代算法進行實現,步驟如下: 1)迭代次數為奇數。 利用格式A1~A8依次對子域Ω1~Ω8中的網格點由外向內進行迭代。 2)迭代次數為偶數。 利用格式A9求解網格中心交叉點(p,q,r),(p+1,q,r),(p,q+1,r),(p+1,q+1,r),(p,q,r+1),(p+1,q,r+1),(p,q+1,r+1),(p+1,q+1,r+1)。 利用格式A10求解內邊界點(p,j,r),(p+1,j,r),(p,j,r+1)和(p+1,j,r+1),j=q+2,q+3,…,m;利用格式A11求解內邊界點(p,j,r),(p+1,j,r),(p,j,r+1)和(p+1,j,r+1),j=q-1,q-2,…,1;利用格式A12求解內邊界點(i,q,r),(i,q+1,r),(i,q,r+1)和(i,q+1,r+1),i=p-1,p-2,…,1;利用格式A13求解內邊界點(i,q,r),(i,q+1,r),(i,q,r+1)和(i,q+1,r+1),i=p+2,p+3,…,l;利用格式A14求解內邊界點(p,q,k),(p,q+1,k),(p+1,q,k)和(p+1,q+1,k),k=r+2,r+3,…,n;利用格式A15求解內邊界點(p,q,k),(p,q+1,k),(p+1,q,k)和(p+1,q+1,k),k=r-1,r-2,…,1。 利用格式A8~A1依次對子域Ω1~Ω8中的網格點由里向外進行迭代。 3)驗證收斂性,若收斂,轉到步驟4),否則回到步驟1)步繼續迭代計算。 4)算法停止。 3.1柱形IEC裝置計算 (1)問題描述 為了對該算法的準確性與快速性進行驗證,現考慮如下三維泊松問題,以圓柱形慣性靜電約束電推力器(IECT)模型為實例進行模擬,不考慮等離子體的影響。 圖3 柱形IEC裝置電勢分布Fig.3 Potential distribution of cylindrical IEC device (2)結果比較 對該方法的快速性進行研究,將其與現在常用的泊松方程迭代方法進行對比分析,結果如表1所示。 表1 多種迭代格式在不同終止條件下的求解時間Table 1 Solution time of various iterative schemes under different termination conditions ms 注:超松弛因子取為ω=1.6,為模擬求得的較快系數,可以嘗試其他值。 從表1可以看出,對于不同的迭代終止條件,P-SOR相較于其他算法的求解時間均大幅領先,可見其快速性是較為穩定的。 3.2 球形IEC裝置計算 (1)問題描述 對該算法適用的廣泛性開展進一步研究,參考斯圖加特大學對于球形IEC裝置的研究進展[16],該裝置如圖4所示,對該裝置進行簡化模擬,不考慮等離子體的影響。 圖4 球形IEC裝置Fig.4 Spherical IEC device (2)結果分析 使用該P-SOR算法對于柱狀或者球狀等結構都能較為精確地計算出與實際情況一致的結果,并與串行運算結果相符。 圖5 球形IEC裝置電勢分布Fig.5 Potential distribution of spherical IEC device 進一步地,對超松弛系數ω進行研究,統計多次計算中ω對收斂所需步數的影響,結果如圖6所示。可以看出,超松弛系數的選取對求解速度的影響十分顯著,和標準形式的超松弛收斂情況類似,極值出現在0<ω<2范圍內,本例在取ω值為1.6左右收斂速度最快。而在極值點之后可能會出現不收斂的情況,所以應慎重選取合適的超松弛系數。 圖6 迭代步數隨超松弛因子的變化關系Fig.6 Relationship between number of iterations and relaxation factor 本文給出的新型P-SOR迭代格式可以很好地對電推力器中復雜電場三維區域進行迭代求解,具有經典SOR格式所沒有的顯式與并行性。較傳統迭代算法快速性顯著,至少快出1/2以上,對于求解航天領域研究中的大型三維泊松問題具有非常重要的現實意義。 當然,該方法現階段尚存在不足,其求解時間距離理論值有一定差距,沒有達到只用一種格式求解時間的1/8。究其原因是該并行算法較經典算法復雜許多,其串行計算部分也占據不小的比重,這都導致對其計算時間造成影響。下一步工作需要對算法進行優化,減小串行求解部分占用的比例。而且隨著所調用的線程數不斷增多,計算機性能越來越好,可以對該方法進行延伸,分解出更多的區域并行求解,使求解速度進一步提高。 References) [1] TSKHAKAYA D.The particle-in-cell method[J].Contri-butions to Plasma Physics,2010,47(8-9):563-594. [2] 陳茂林,夏廣慶,魏延明,等.電動帆平行雙導線鞘層特性與受力分析[J].物理學報,2016,65(20):279-289. CHEN M L,XIA G Q,WEI Y M,et al.Charateristics and stress analysis of sheath of parallel conducting tethers for the electric sail[J].Acta Physica Sinica,2016,65(20):279-289(in Chinese). [3] 劉輝,羅曉明,溫正,等.GEO衛星霍爾推力器羽流防護結構混合PIC模擬[J].中國空間科學技術,2016,36(1):63-69. LIU H,LUO X M,WEN Z,et al.Hybrid-PIC simulation of Hall thruster plume shield on GEO satellites[J].Chinese Space Science and Technology,2016,36(1):63-69(in Chinese). [4] 孫安邦,毛根旺,陳茂林,等.霍爾效應推力器羽流的PIC/MCC模擬[J].固體火箭技術,2009,32(6):638-643. SUN A B,MAO G W,CHEN M L,et al.PIC/MCC simulation of Hall effect thruster plume[J].Journal of Solid Rocket Technology,2009,32(6):638-643. [5] MARTINS S F,FONSECA R A,LU W,et al.Exploring laser-wakefield-accelerator regimes for near-term lasers using particle-in-cell simulation in Lorentz-boosted frames[J].Nature Physics,2010,6(4): 311. [6] SAMEH A H.On Jacobi and Jacobi-like algorithms for a parallel computer[J].Mathematics of Computation,1971,25(115): 579-590. [7] 蔡放,方逵,李彬.具有完全并行度的SOR算法[J].高等學校計算數學學報,2002,24(1):11-14. CAI F,FANG K,LI B.Parallel computation with the perfect degree of parallelism for SOR [J].Numerical Mathematics A Journal of Chinese Universities,2002(1):11-14. [8] 岳小寧,肖炳甲,羅正平.基于CUDA的二維泊松方程快速直接求解[J].計算機科學,2013,40(10):21-23. YUE X N,XIAO B J,LUO Z P.Fast 2-dimension Poisson direct solver based on CUDA[J].Computer Science,2013,40(10):21-23(in Chinese). [9] YOUNG D M,KINCAID D R.A new class of parallel alternating-type iterative methods[J].Journal of Computational & Applied Mathematics,1970,74(1-2):331-344. [10] 馬月珍,葛永斌,王燕.三維泊松方程基于Richardson外推法的高階緊致差分方法[J].數學的實踐與認識,2011,41(8):146-152. MA Y Z,GE Y B,WANG Y.A high-order compact difference method based on Richardson extrapolation for the 3D Poisson equation[J].Mathematics in Practice & Theory,2011,8(8):146-152(in Chinese). [11] QUINN M J.Parallel programming in C with MPI and OpenMP[M].New York:McGraw-Hill,2003: 436-513. [12] MOTOYASU T,NAMBA S,TAKIYAMA K.Mea-surements of localized potential profiles by LIF polarization spectroscopy in an inertial-electrostatic confinement discharge[J].Journal of the Korean Physical Society,2014,65(8):1205-1208. [13] 豆桂芳,吳振遠,杜艷林.三維泊松方程的七點差分格式[J].工程地球物理學報,2009,6(6):802-805. DOU G F,WU Z Y,DU Y L.The seven-point difference scheme for the three-dimensional Poisson's equation[J].Chinese Journal of Engineering Geophysics,2009,6(6):802-805(in Chinese). [14] 許秋燕.二維泊松方程和擴散方程的一類顯式并行算法[D].濟南:山東大學,2010:2-14. XU Q Y.A class of explicit parallel algorithms for 2d Poisson and diffusion equations[D].Jinan: Shandong University,2010:2-14(in Chinese). [15] 李春光,徐成賢.確定SOR最佳松弛因子的一個實用算法[J].計算力學學報,2002,19(3):299-302. LI C G,XU C X.A practical algorithm determining the optimal relaxation factor of SOR iterative methods[J].Chinese Journal of Computational Mechanics,2002,19(3):299-302(in Chinese). [16] CHAN Y A,HERDRICH G,SYRING C,et al.An approach for thrust and losses in inertial electrostatic confinement devices for electric propulsion applications[C].International Electric Propulsion Conference.Kobe:IEPC,2015:083. (編輯:車曉玲) Successiveoverrelaxationparallelalgorithmforsolvingcomplexelectricfieldinelectricthrusters HAN Yajie1,XIA Guangqing1,*,WU Qiuyun1,CHEN Liuwei1,ZHOU Niandong1,WEN Zheng2 1.StateKeyLaboratoryofStructureAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,China2.InstituteofTelecommunicationSatellite,ChinaAcademyofSpaceTechnology,Beijing100094,China At present,solving the three-dimensional Poisson equation of complex electric field in the electric thruster still has the disadvantages of slowness and poor parallelism.A successive over relaxation parallel (P-SOR)iterative algorithm was proposed to solve the three-dimensional Poisson equation based on the idea of domain decomposition.The solution region was divided into several sub-domains.And a number of explicit schemes were constructed by using the SOR method.Then according to the different schemes,the solving equations for different iterative steps were given for parallel computation.The numerical simulation results show that the calculation time is reduced by at least half.And the P-SOR method has made great progress in the computation speed compared with the traditional iterative scheme. electric thruster;Poisson equation;successive over relaxation iteration;parallel algorithm http://zgkj.cast.cn 10.16708/j.cnki.1000-758X.2017.0074 V430 A 2017-03-21; 2017-08-09;錄用日期2017-09-12;< class="emphasis_bold">網絡出版時間 時間:2017-09-24 16:01:22 http://kns.cnki.net/kcms/detail/11.1859.V.20170924.1601.012.html 國家自然科學基金(11675040);遼寧省自然科學基金(201602175);軍委科技委H863項目(17-H863-03-ZT-005-072-01) 韓亞杰(1993-),男,碩士研究生,442300107@qq.com,研究方向為電推進數值模擬與計算 *通訊作者:夏廣慶(1979-),男,副教授,gq.xia@dlut.edu.cn,研究方向為電推進技術 韓亞杰,夏廣慶,吳秋云,等.電推力器中復雜電場求解的超松弛并行算法[J].中國空間科學技術,2017,37(5):68-74.HANYJ,XIAGQ,WUQY,etal.Successiveoverrelaxationparallelalgorithmforsolvingcomplexelectricfieldinelectricthrusters[J].ChineseSpaceScienceandTechnology,2017,37(5):68-74(inChinese).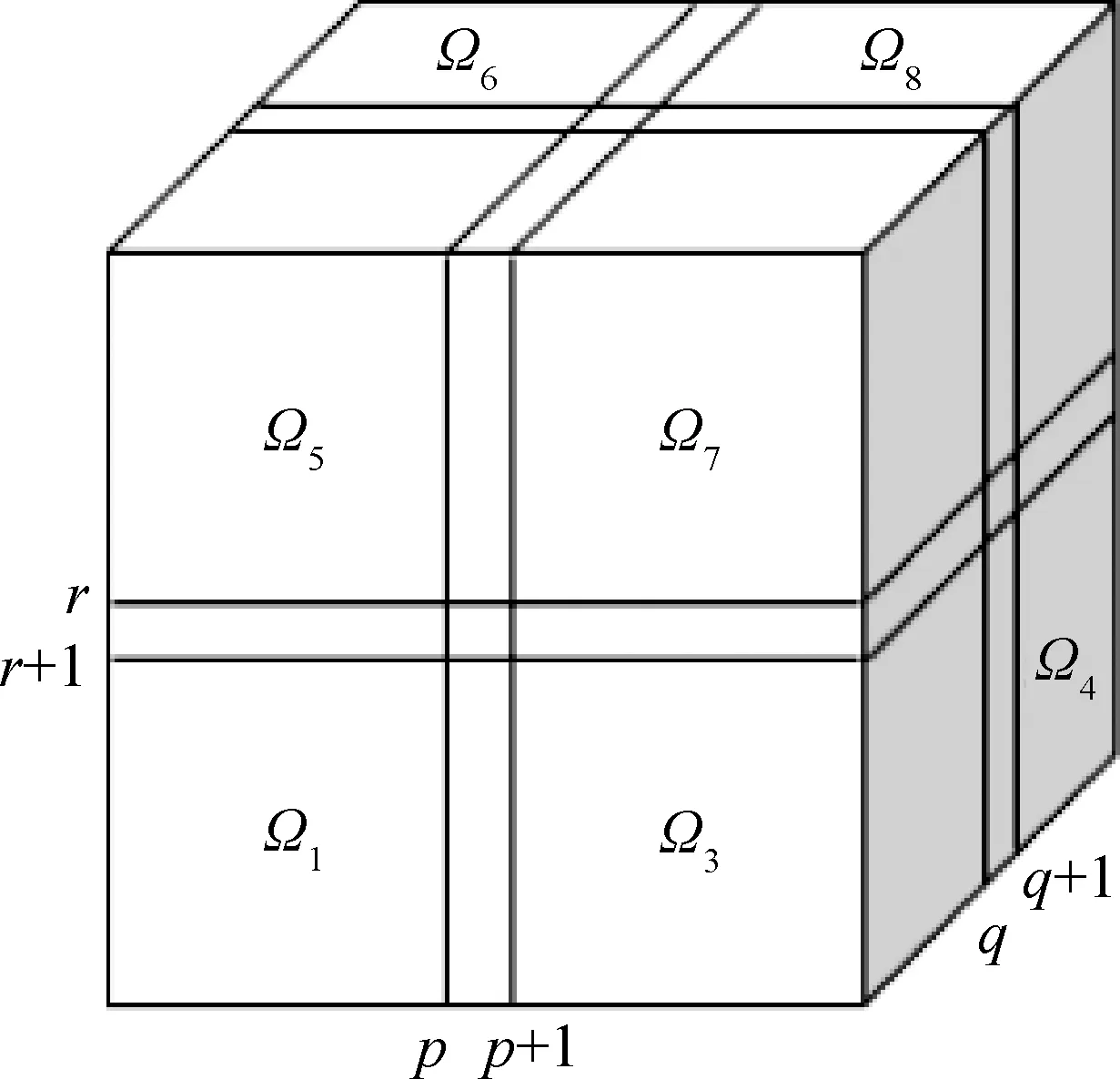
3 數值算例

4 結束語

