傾轉旋翼機動態傾轉過渡過程的操縱策略優化

嚴旭飛,陳仁良*

南京航空航天大學 直升機旋翼動力學國家級重點實驗室,南京 210016

傾轉旋翼機動態傾轉過渡過程的操縱策略優化

嚴旭飛,陳仁良*

南京航空航天大學 直升機旋翼動力學國家級重點實驗室,南京 210016

利用最優控制方法研究傾轉旋翼機的最優動態傾轉過渡過程,并得到最優操縱策略,使得由時間、姿態角變化以及駕駛員工作負荷等組成的性能指標達到最小。首先,在基本縱向剛體飛行動力學模型的基礎上引入混合操縱方程,并使用桿量位移的一階導數作為控制量,形成適用于計算傾轉旋翼機動態傾轉過渡過程的飛行動力學模型,從而能在動態傾轉操縱策略優化過程中考慮到操縱系統特性對操縱量變化速度的限制,以及避免操縱量在優化過程中出現跳躍不連續。然后,將傾轉旋翼機的最優動態傾轉過渡過程轉化為非線性動態最優控制問題,建立合理的性能指標,并采用直接轉換法和序列二次規劃算法進行求解。最后,以XV-15傾轉旋翼機為樣機,分別計算正向和逆向最優動態傾轉過渡過程,并與駕駛員飛行仿真數據進行對比。結果表明:飛行狀態量的時間歷程與文獻吻合地較好,且俯仰姿態角和桿量位移變化更加柔和。最優控制方法可以用于研究傾轉旋翼機的最優動態傾轉過渡過程。

最優控制;傾轉旋翼機;動態傾轉過渡;性能指標;序列二次規劃

傾轉旋翼機是一種將直升機和固定翼飛機特點融為一體的新型飛行器,具有廣泛的應用前景。傾轉旋翼機具有3種飛行模式:直升機模式、固定翼飛機模式以及傾轉過渡模式。為了滿足直升機模式和固定翼飛機模式的要求,傾轉旋翼機同時具有直升機和固定翼2套操縱方式,并隨著發動機短艙傾轉角的改變而逐漸轉換。因此傾轉旋翼機在傾轉過渡過程中會出現操縱冗余問題,駕駛員操縱會變得十分復雜。除此之外,整個傾轉過渡過程還必須保證在短艙傾轉角-速度包線內完成,這是因為過低的前飛速度會導致傾轉旋翼機機翼失速,過高的前飛速度則會受到旋翼前行槳葉壓縮性、后行槳葉失速以及旋翼可用功率的限制。可以看出,傾轉旋翼機的傾轉過渡過程是極為重要和復雜的飛行過程,如何解決操縱冗余問題,并讓傾轉旋翼機順利地完成直升機模式和固定翼飛機模式之間的相互轉換,是國內外研究的重要課題。

目前關于傾轉旋翼機傾轉過渡的控制方法主要集中在預先設定操縱方案以解決操縱冗余問題,并設計控制系統來跟蹤預定指令(傾轉規律、飛行軌跡等)上[1-4],無法得到不同飛行任務下整個傾轉過渡過程的最優操縱策略和飛行軌跡[5-9]。事實上,研究傾轉旋翼機的最優傾轉過渡過程,得到對應的操縱策略和飛行軌跡等,不僅可以解決操縱冗余問題,還能有效降低駕駛員工作負荷、提高傾轉過渡效率、穩定機體姿態,有利于傾轉過渡系統的設計,因此有必要對傾轉旋翼機的最優傾轉過渡過程進行研究。

傾轉旋翼機在傾轉過渡過程中的最優動態傾轉問題可以描述為:從一類允許的傾轉過渡操縱策略中找出1個最優的操縱策略,使傾轉旋翼機在該操縱策略作用下由初始狀態模式傾轉到指定的目標狀態模式的同時,其評價運動過程品質優劣的性能指標為最優。在整個傾轉過程中,飛行器的運動、操縱策略與性能指標均為時間和空間的函數,因此傾轉旋翼機的最優動態傾轉問題可以歸結為一種含有狀態和控制約束的非線性動態最優控制問題。該問題可以采用最優控制方法進行求解。最優控制方法廣泛應用于傾轉旋翼機發動機失效后軌跡優化的研究,該方法不僅可以解決傾轉旋翼機發動機失效后駕駛員的操縱冗余問題[10-13],還能得到最優操縱策略和飛行軌跡[14-17]。目前尚未有文獻將該方法應用于研究傾轉旋翼機的最優動態傾轉過渡過程。

因此,本文采用最優控制方法研究傾轉旋翼機的最優動態傾轉過渡過程。首先以傾轉旋翼機基本飛行動力學模型為基礎,引入混合操縱方程,并使用駕駛員操縱量的一階導數作為控制量,形成適用于計算傾轉旋翼機動態傾轉過渡過程的飛行動力學模型,從而能在動態傾轉操縱策略優化過程中考慮到操縱系統特性對操縱量變化速度的限制,以及避免操縱量在優化過程中出現跳躍不連續。然后,以傾轉旋翼機的飛行狀態量、駕駛員操縱量和控制量為優化變量,將傾轉旋翼機動態傾轉過渡過程轉化為非線性動態最優控制問題,建立合適的性能指標,并采用直接轉換法和序列二次規劃算法進行求解。最后,以XV-15傾轉旋翼機為樣機,分別計算正向以及逆向最優動態傾轉過渡過程,并與相關駕駛員飛行仿真數據進行對比,以驗證利用最優控制方法研究傾轉旋翼機最優動態傾轉過渡過程的可行性。

1 飛行動力學建模

傾轉旋翼機具有沿縱向對稱構型,在無側風條件下,傾轉過渡過程都在縱向平面。為了提高最優控制方法的計算效率,本文以基本縱向剛體飛行動力學模型為基礎,引入混合操縱方程,并使用桿量位移的一階導數作為控制量,形成適用于計算傾轉旋翼機動態傾轉過渡過程的飛行動力學模型。

1.1 基本飛行動力學模型

模型狀態變量為:體軸系中的縱向速度u和垂向速度w,俯仰角速度q,俯仰角θ,水平位移x,高度h;控制變量為:槳根總距θ0、縱向周期變距θs,升降舵偏轉角θe和短艙傾轉角in。運動方程可以表示為

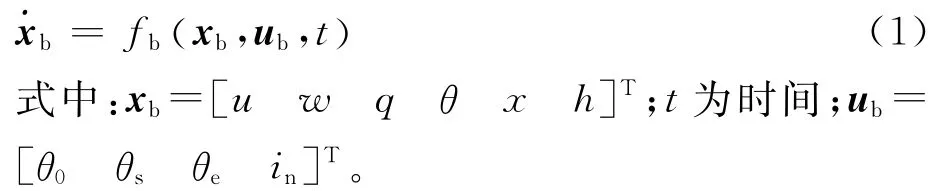
考慮到旋翼尾流對機翼的干擾,將機翼-短艙的氣動力分為兩部分:一部分為受到旋翼尾流影響的機翼氣動力,另一部分為不受旋翼尾流作用的機翼氣動力。機翼處于旋翼滑流部分的面積Swss和處于自由流部分的面積Swfs的計算公式分別為[15]

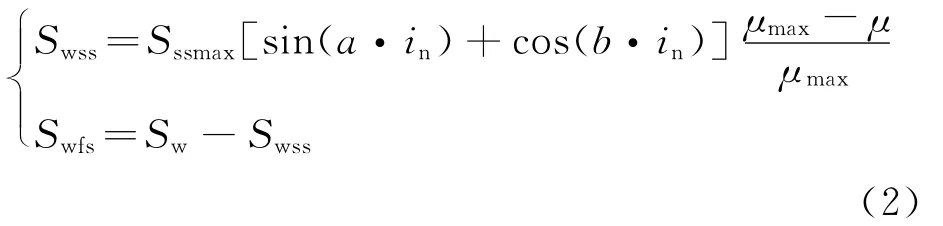
式中:Sssmax=2ηssRc,ηss為旋翼滑流修正因子,R為旋翼半徑,c為機翼平均氣動弦長;a=1.386;b=3.114;μ為旋翼前進比;μmax為旋翼尾跡偏出機翼的最大前進比;Sw為機翼面積。

各部件的氣動力和力矩系數均取自XV-15傾轉旋翼機的吹風數據[18],其中受旋翼尾流作用的機翼部分氣流速度需要加上旋翼誘導速度的影響。

1.2 混合操縱方程

根據傾轉旋翼飛行器的操縱特點,建立適用于全部飛行模式的混合操縱方程,以解決操縱冗余問題。

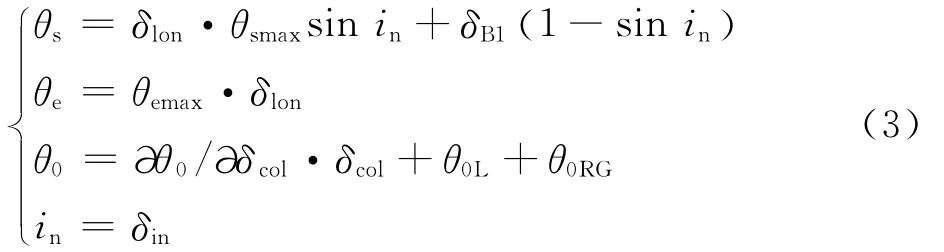
傾轉旋翼機駕駛員通過總距桿位移δcol改變旋翼槳根總距θ0,通過縱向桿位移δlon改變縱向周期變距θs和升降舵偏轉角θe,并通過拇指滾輪δin來改變發動機短艙傾轉角in。直升機模式下,縱向周期變距和總距的操縱與常規直升機的操縱相同,但是當短艙傾轉角in逐漸減小(由直升機模式變為固定翼飛機模式)時,縱向周期變距操縱和總距操縱效能逐漸減弱。這個過程可以表示為[18]式中:縱向周期變距桿量δlon和總距桿量δcol的無量綱操縱行程(采用各自對應的總操縱行程進行無量綱化)均為0～1;拇指滾輪δin的操縱行程為0°～95°;θsmax為最大縱向周期變距;補償量δB1為1.5°;θemax為升降舵最大偏轉角。總距系數?θ0/?δcol和總距補償角θ0L與短艙傾轉角in有關,總距管理器輸出角θ0RG與in、δcol和合速度VT有關[18-19],因此旋翼槳根總距θ0可以表示為in、δcol和VT的函數。

混合操縱方程式(3)將發動機短艙傾轉角in、槳根總距θ0、縱向周期變距θs以及升降舵θe這4個操縱量減少為駕駛員的拇指滾輪δin、總距桿δcol和縱向操縱桿δlon這3個操縱量,這樣既可以減少操縱變量,又可以得到駕駛員的操縱信息。

本文通過最優控制方法即可求出不同飛行任務下動態傾轉過渡過程中駕駛員3個操縱量的最優時間歷程,從而解決操縱冗余問題。

考慮到操縱系統特性對操縱量變化速度的限制,同時為了避免操縱量在數值優化過程中出現跳躍不連續或者“bang-bang”型控制的形式[11],使用{δcol,δlon,δin}的一階導數{uc,us,un}作為控制量,并把{δcol,δlon,δin}作為新的狀態變量,即

式(1)、式(3)、式(4)組成了適用于計算傾轉旋翼機動態傾轉過渡過程的飛行動力學模型,其狀態空間形式為

1.3 模型驗證

本文以XV-15傾轉旋翼機為樣機進行最優動態傾轉過渡過程的研究,飛行器的基本參數見表1(詳細參數見文獻[18])。

表1 XV-15傾轉旋翼機基本參數［18］Table 1 Basic parameters of XV-15 tilt-rotor aircraft［18］

圖1所示為本文模型配平狀態與飛行試驗數據的對比,其中Pr為需用功率。飛行試驗數據來自于XV-15的驗證報告[19],飛行器參數與本文所用樣機一致。圖中短艙傾角為90°時的襟翼/副翼配置為40°/25°,60°時襟翼/副翼配置為20°/12.5°,0°時襟翼/副翼配置為0°/0°。從圖中可以看出,計算結果和飛行試驗數據吻合較好,本文建立的飛行動力學模型較為準確,可以用來研究傾轉旋翼機的最優動態傾轉過程。本文假設傾轉旋翼機在開始進行傾轉過渡時,飛行器處于穩定飛行狀態,因此本節計算的平衡狀態可以為動態傾轉優化提供初始值。

2 動態最優控制問題

傾轉旋翼機的最優動態傾轉過渡問題可以等效為一種含有狀態和控制約束的非線性動態最優控制問題。最優控制問題一般由性能指標、微分方程、邊界條件和路徑約束組成[10]。

1)性能指標

傾轉旋翼機在傾轉過渡過程中,旋翼的拉力方向以及全機重心會發生變化,導致俯仰姿態變化較大,需要駕駛員通過適當的操縱來穩定姿態,因此性能指標需要考慮到對俯仰姿態的控制。此外,還應該考慮傾轉過渡過程所需時間和駕駛員的工作負荷,故性能指標可以定為

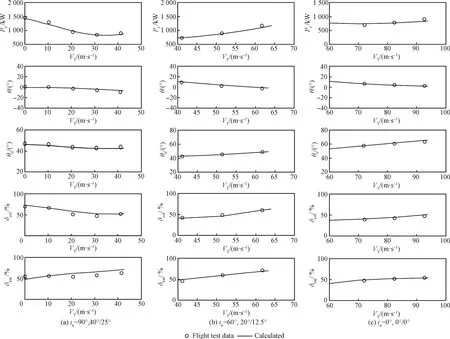
圖1 計算配平狀態與飛行試驗數據[19]對比Fig.1 Calculated trim vs flight test data[19]

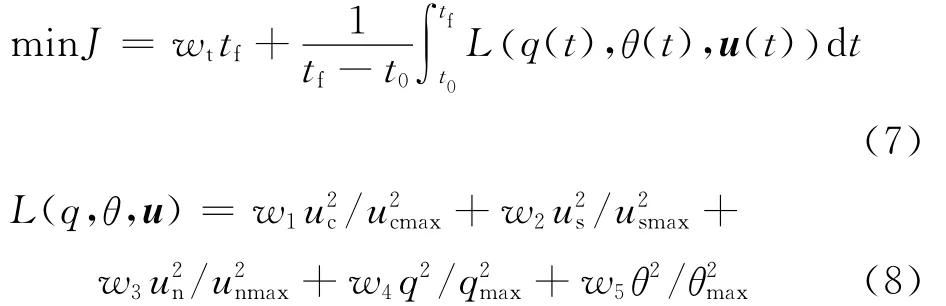
式中:t0為初始時刻;tf為末端時刻;ucmax、usmax、unmax分別為3個控制量的最大值;qmax、θmax分別為允許的最大俯仰角速度和俯仰角度;wt、w1、w2、w3、w4、w5為常數權重系數,權重系數越大,對應項越重要。在傾轉過渡過程中,駕駛員一般通過拇指滾輪讓發動機短艙以固定的角速率進行傾轉,并主要專注于對總距桿和縱向桿的控制[5,8-9],因此uc和us對應的權重系數w1和w2要大一些。在傾轉過渡過程中,由于俯仰角變化較大,因此俯仰角速率和俯仰角對應的權重系數w4和w5也要大一些。本文通過大量仿真調試得出如下權重系數:wt=1.0,w1=w2=2.0,w3=1.0,w4=w5=1.5。

本文在性能指標中暫不考慮對軌跡的控制(縱向平面內為高度控制),是為了讓駕駛員可以著重于穩定姿態的操縱,從而降低操縱難度。至于傾轉過渡過程中的高度變化,可以在路徑約束中根據不同飛行任務要求進行約束,使其保持在可接受的范圍內即可。

2)微分方程

采用適用于計算傾轉旋翼機動態傾轉過渡過程的飛行動力學模型式(5)。

3)邊界條件

操縱策略優化初始邊界條件為飛行器當前飛行狀態;為了方便研究,將末端邊界條件設定為目標傾轉角度以及前飛速度,即

式中:int為目標發動機短艙傾轉角度;˙xt為目標前飛速度,具體數值根據飛行任務要求確定。

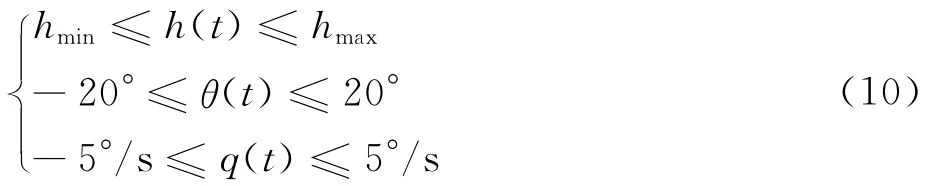
4)路徑約束

為了讓高度保持在可接受的范圍內,在路徑約束中根據不同的飛行任務要求對高度h變化進行了一定的限制。此外,在路徑約束中對俯仰姿態角θ和角速率q也進行限制:

式中:hmin和hmax分別為允許的最小和最大高度。

利用傾轉旋翼機短艙傾轉角-速度包線分析方法[20]確定路徑約束,可以使動態傾轉過渡過程保持在短艙傾轉角-速度包線內。

低速傾轉時,機翼提供的升力受機翼臨界失速迎角的限制,因此在處于低速段傾轉包線時,機翼迎角處于機翼臨界迎角,此時滿足的關系為[20]αw=αwc=iw+αf(11)式中:αw為機翼迎角;αwc為機翼臨界迎角;iw為機翼安裝角(0°);αf為機身迎角。由低速段發動機短艙傾轉角度-速度包線確定的不等式路徑約束為

式中:αwcmin和αwcmax分別為最小臨界迎角和最大臨界迎角,可由吹風數據得到,在本文中分別為-20°和12°。

傾轉過程中的最大前飛速度受旋翼前行槳葉壓縮性與后行槳葉失速效應以及旋翼可用功率與動力穩定性等限制,其中旋翼可用功率的限制是最基本和最重要的限制要素。因此處于高速段傾轉包線時,旋翼的總需用功率達到發動機輸出的額定功率[20]。

旋翼需用功率系數CP為[15]

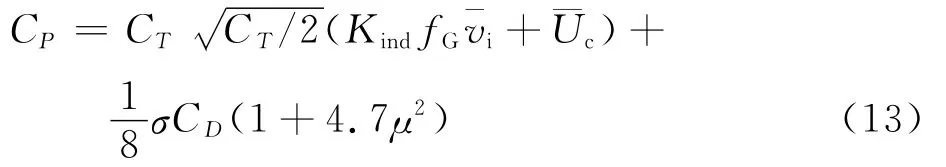
式中:CT為旋翼拉力系數;Kind為誘導速度修正因子;fG為地面效應因子;ˉvi為無量綱誘導速度;ˉUc為垂直于旋翼槳盤的無量綱氣流速度;σ為旋翼實度;CD為旋翼槳葉阻力系數。則傾轉旋翼機需用功率Pr可以表示為[15]

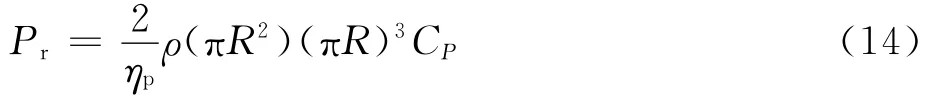
式中:ηp為傳動功率損失因子;ρ為空氣密度。

由高速段發動機短艙傾轉角度-速度包線確定的不等式路徑約束為

式中:Pcr為發動機輸出的額定功率(1 737.5 k W)。為了進一步確保傾轉過渡過程的飛行安全,把高速段傾轉包線上發動機短艙傾轉角45°對應的速度作為中止速度[20],傾轉過程飛行速度不能大于中止速度Vstop(在本文中為88 m/s),即整個動態傾轉過渡過程中,駕駛員的操縱速

率可以根據傾轉旋翼機的助力器速率限制[18]確定,即

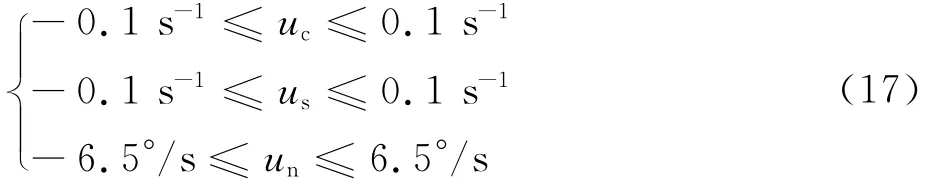
3 最優控制數值解法

傾轉旋翼機最優動態傾轉對應的最優控制問題的狀態和控制變量眾多,約束和目標函數非常復雜,故解析求解不可行,需要通過數值優化算法來進行求解。本文采用直接轉換法將該非線性動態最優控制問題轉化為非線性規劃問題,并用具有良好魯棒性和計算效率的序列二次規劃算法來求解。

3.1 無量綱縮放

在進行數值計算時,由于狀態變量和控制變量的量綱不同,某些變量之間的數量級相差較大,會引起數值求解困難。所以首先對飛行動力學模型中的參數進行無量綱縮放。

定義常數k1、k2、k3、k4對狀態量、控制量和時間進行無量綱縮放:

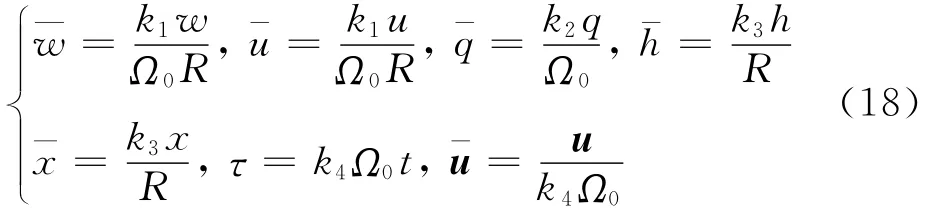
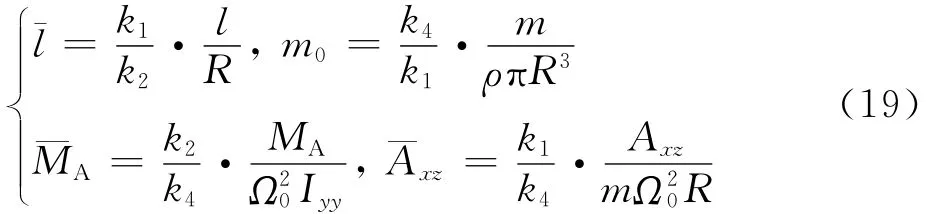
式中:Ω0為標準旋翼轉速。長度l、質量m、氣動力Axz和氣動力矩MA的無量綱縮放如下:

式中:Iyy為俯仰慣性矩。為了使無量綱縮放后的狀態變量和控制變量大小接近1,取k1=k2=100,k3=1,k4=0.01。

無量綱縮放后的飛行動力學狀態方程可以表示為

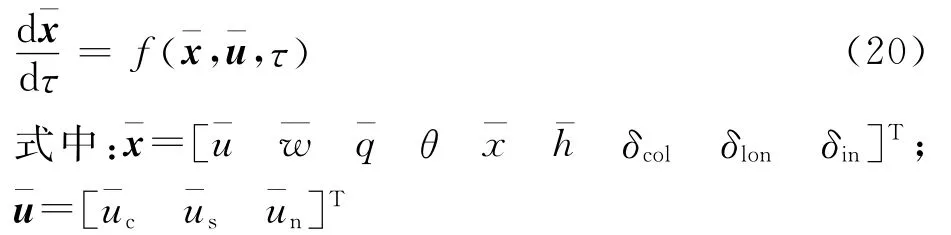
3.2 直接轉換法

將時間的無量綱τ等分為N-1個時間段:

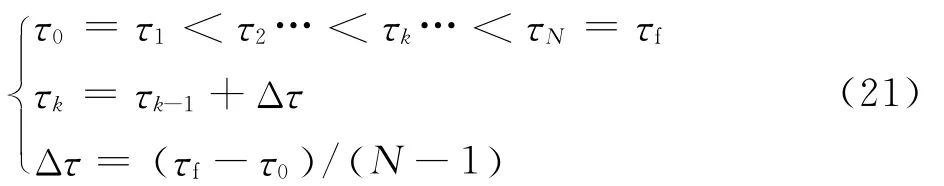
使用Hermite-Simpson節點配置方法把連續空間下的狀態變量和控制變量進行離散,得到非線性規劃問題的設計變量,其原理如圖2所示。則離散后的設計變量為

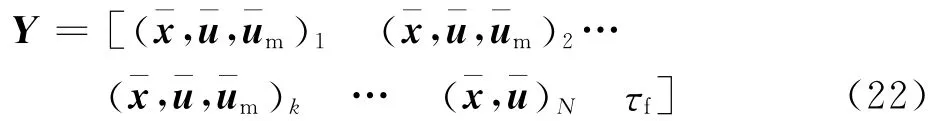
其中對動態最優控制問題中的微分方程進行離

散,得到缺陷等式約束方程為

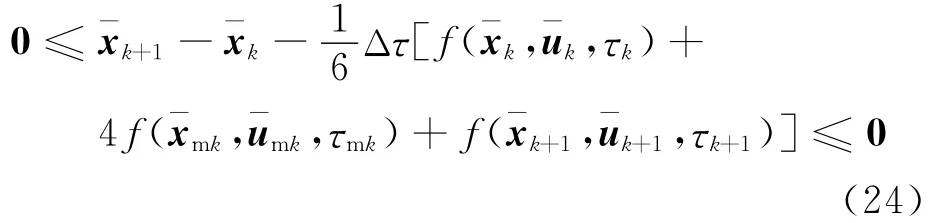
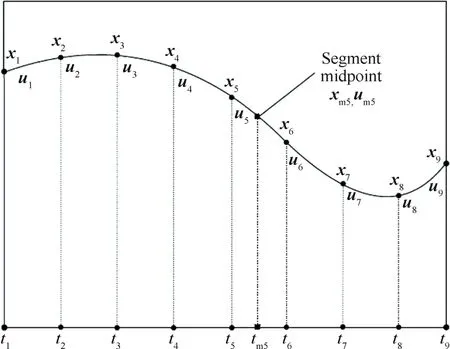
圖2 直接轉換法Fig.2 Direct transcription method

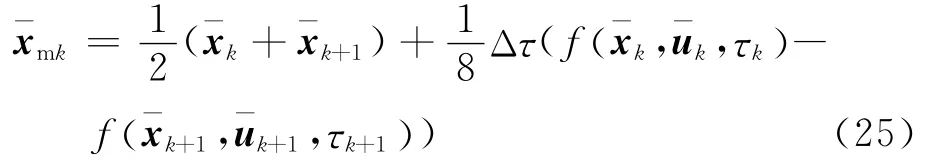
對性能指標進行離散得到

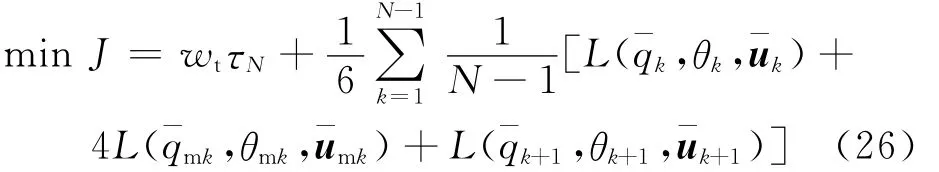
邊界條件作用于最后一個節點:

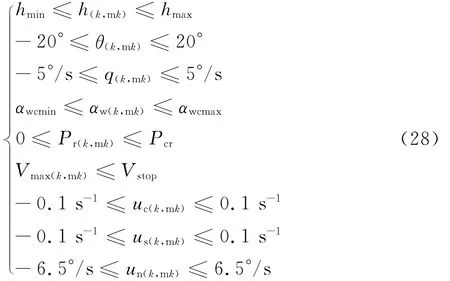
路徑約束作用于每一個時間段節點和中間節點:

將非線性動態最優控制問題轉化為非線性規劃問題后,應用稀疏序列二次規劃算法[21]求解該非線性規劃問題即可得到最優解。序列二次規劃算法可以很好地解決有大量設計變量和約束方程的非線性規劃問題。最后對最優解中所有節點處的狀態變量和控制變量進行分段3次Hermite插值,得到更光滑的桿量變化、傾轉規律和飛行軌跡等。

4 動態傾轉過渡操縱策略優化

利用本文建立的飛行動力學模型分別計算正向以及逆向最優動態傾轉過渡過程。并與文獻[9]中的相關駕駛員飛行仿真數據進行對比,以驗證利用最優控制方法研究傾轉旋翼機最優動態傾轉過渡過程的可行性。文獻[9]中的仿真數據是由駕駛員在XV-15飛行仿真設備中進行傾轉過渡飛行模擬試驗得到的,所用機型參數與本文一致。

本文之所以和文獻[9]中的駕駛員飛行仿真數據對比,是因為在該文獻中駕駛員可以根據當前飛行任務自行決定傾轉過渡過程中的操縱策略和對應的飛行軌跡,而不需要去跟蹤預定的飛行軌跡和操縱方案。本文建立的方法正好可以用于求解該類飛行任務下的最優操縱策略和飛行軌跡,所以可以用來對比。

4.1 正向動態傾轉過渡

本節以XV-15傾轉旋翼機由直升機模式向固定翼飛機模式連續正向傾轉為例,利用最優控制方法進行操縱策略優化,并與文獻[9]中的駕駛員飛行仿真結果進行對比。文獻[9]中駕駛員進行正向傾轉過渡時的初始狀態如下:速度為32 m/s,高度為88 m,航跡角為7°,此時飛行器處于穩定飛行狀態。飛行任務要求駕駛員自行決定操縱策略,允許高度變化,傾轉結束后速度保持為65 m/s。為了方便對比,本文計算正向最優動態傾轉過渡過程時的初始狀態和飛行任務設置與文獻[9]保持一致。

根據當前飛行任務,目標發動機短艙傾轉角度int為0°,目標前飛速度˙xt為65 m/s,路徑約束中將高度h的范圍定為

80 m≤h(t)≤150 m (29)

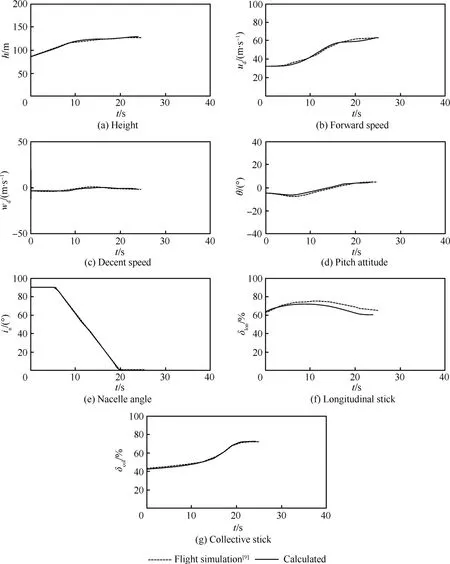
圖3 正向動態傾轉過渡最優解Fig.3 Optimal solution for accelerating dynamic conversion

圖3所示為本文計算的正向動態傾轉的最優操縱策略以及對應的飛行狀態量的時間歷程,其中,ud為地軸系前飛速度,wd為地軸系下降速度。可以看出,發動機短艙以6.5°/s的角速度直接傾轉至固定翼飛機模式,期間駕駛員緩慢增大總距桿位移并向前推桿,前飛速度增大,隨后向后拉桿穩定姿態。整個正向傾轉過渡過程的操縱策略較為容易實現,且飛行狀態量變化平穩。本文計算結果與文獻[9]中駕駛員模擬仿真結果較為接近,且俯仰角變化更加平穩。

4.2 逆向動態傾轉過渡

本節以XV-15傾轉旋翼機由固定翼飛機模式向直升機模式連續逆向傾轉為例,利用最優控制方法進行操縱策略優化,并與文獻[9]中的駕駛員飛行仿真結果進行對比。逆向傾轉過渡時的初始狀態如下:速度為62 m/s,高度為120 m,航跡角為-2°,處于穩定飛行狀態,飛行任務要求駕駛員自行決定操縱策略和飛行軌跡,最后需要著陸。為了方便對比,本文計算逆向最優動態傾轉過渡過程時的初始狀態和飛行任務設置與文獻[9]保持一致。

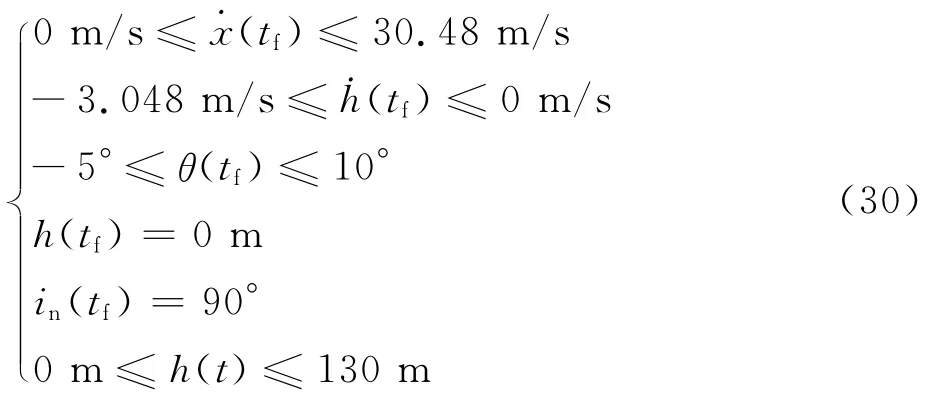
逆向動態傾轉過渡一般涉及到傾轉旋翼機的減速著陸過程,為了滿足適航條例關于安全著陸的要求,需要對動態最優控制問題的末端邊界條件和路徑約束做出以下修改:

式 中:˙x 為 前 飛 速 度;˙h 為 上 升 速 度 。

圖4所示為本文計算的逆向動態傾轉的最優操縱策略以及對應的飛行狀態量的時間歷程。可以看出,發動機短艙以-6.5°/s的角速度直接傾轉至直升機飛機模式,旋翼拉力逐漸增大,駕駛員增大總距桿并向后拉桿,俯仰角上升,前飛速度逐漸減小;傾轉至直升機模式后,駕駛員繼續操縱總距桿和縱向周期變距桿使飛行器安全著陸。與文獻[9]中駕駛員飛行模擬仿真結果相比,本文計算得出的飛行狀態量的時間歷程與文獻吻合地較好,且下降率和俯仰角變化更加平穩,總距桿變化更加柔和。

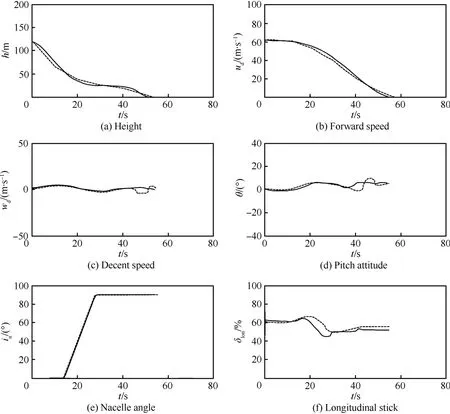
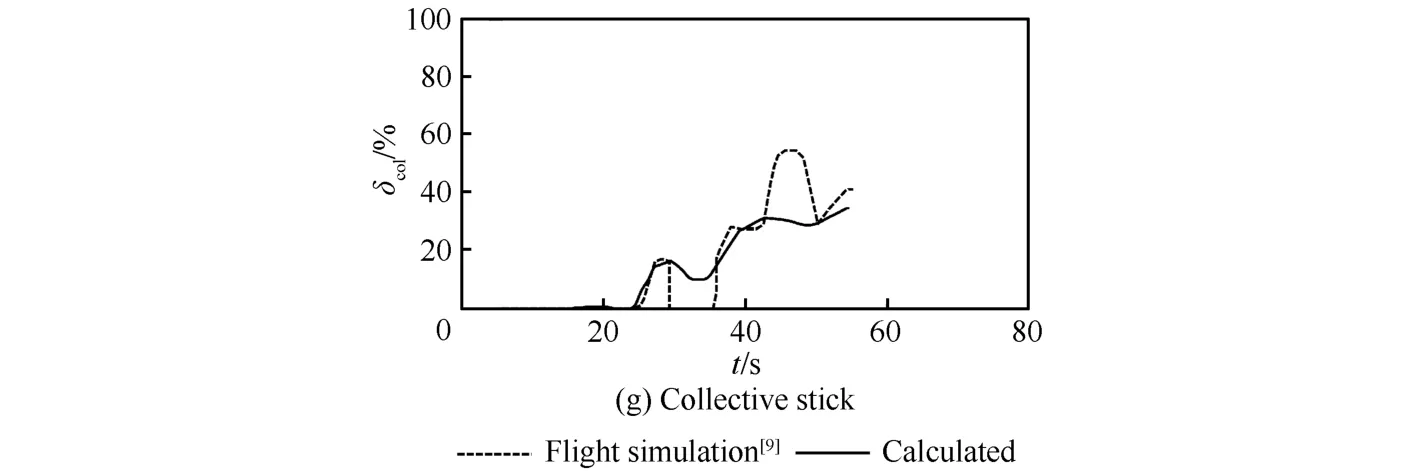
圖4 逆向動態傾轉、減速著陸最優解Fig.4 Optimal solution for decelerating dynamic conversion and landing

4.3 討論與分析

文獻[9]中的飛行仿真結果是由駕駛員在飛行仿真設備中得到的。在傾轉過程中,駕駛員根據當前飛行任務自行決定傾轉過渡過程中的操縱策略和對應的飛行軌跡,因此駕駛員采取的操縱策略并不一定是當前飛行任務下最優的(可以看出逆向動態傾轉時駕駛員總距桿操縱波動較大,使著陸前的俯仰角和下降率變化較大);而本文則是采用數值優化算法得到當前飛行任務下傾轉過渡過程中的最優操縱策略和最優軌跡。在性能指標中,本文主要對駕駛員的操縱速率、俯仰角和俯仰角速率進行控制。最優控制方法會不斷地進行迭代,直到找到使性能指標為最優的操縱策略,該最優操縱策略不僅可以降低駕駛員的工作負荷,還能使俯仰角變化更加平穩。因此本文得到的最優解與駕駛員飛行仿真結果較為接近,且俯仰角變化更加平穩,逆向傾轉過渡時總距桿變化更加柔和,駕駛員工作負荷更低。

5 結 論

1)目前關于傾轉旋翼機傾轉過渡的控制方法主要集中在預先設定操縱方案以解決操縱冗余問題,并設計控制系統來跟蹤預定指令(傾轉規律、飛行軌跡等)上,無法得到不同飛行任務下整個傾轉過渡過程的最優操縱策略和飛行軌跡。本文建立的傾轉旋翼機飛行動力學模型以及采用最優控制方法可以根據不同的飛行任務要求得到傾轉過渡的最優操縱策略和對應的最優飛行軌跡,在解決操縱冗余問題的同時,還可以降低駕駛員工作負荷、提高傾轉過渡效率、穩定機體姿態。

2)本文以XV-15傾轉旋翼機為樣機研究傾轉旋翼機的最優正向和逆向動態傾轉過渡過程,并與文獻[9]中的駕駛員飛行仿真結果進行對比。結果表明:本文得到的最優解與駕駛員根據當前飛行任務采取的操縱策略以及對應的飛行軌跡數據吻合較好;正向動態傾轉時,本文計算得到的俯仰角變化更加平穩;逆向動態傾轉時,本文計算得到的下降率和俯仰姿態角變化更平穩,且總距桿量位移變化也更加柔和。這是因為最優控制方法會通過不斷地迭代直至找到使本文建立的性能指標達到最優的操縱策略,該最優操縱策略不僅可以降低駕駛員的工作負荷,還能使俯仰角變化更加平穩。

3)本文建立的飛行動力學模型以及采用的最優控制方法可用于研究傾轉旋翼機的最優動態傾轉過渡過程,并得到相應的最優操縱策略和飛行軌跡,給駕駛員和設計人員提供一定的參考。下一步將圍繞高置信度傾轉旋翼機模型展開研究,從而可以更加準確地計算不同飛行條件下傾轉旋翼機傾轉過渡過程的最優操縱策略和飛行軌跡。

[1] 王奇,吳文海.一種非線性自適應切換控制混合方法及其在傾轉旋翼機上的應用[J].航空學報,2015,36(10):3359-3369.WANG Q,WU W H.A nonlinear adaptive switching control blending method and its application to tiltrotor[J].Acta Aeronautica et Astronautica Sinica,2015,36(10):3359-3369(in Chinese).

[2] 夏青元,徐錦法,金開保.傾轉旋翼飛行器的建模和操縱分配策略[J].航空動力學報,2013,28(9):2016-2028.XIA Q Y,XU J F,JIN K B.Tilt-rotor aircraft modeling and its manipulation assignment strategy[J].Journal of Aerospace Power,2013,28(9):2016-2028(in Chinese).

[3] 陳永,龔華軍,王彪.傾轉旋翼機過渡段縱向姿態控制技術研究[J].飛行力學,2011,29(1):30-33.CHEN Y,GONG H J,WANG B.Research on longitudna1 attitude contro1 technology of tilt rotor during transition[J].Flight Dynamics,2011,29(1):30-33(in Chinese).

[4] PU H Z,ZHEN Z Y,GAO C.Tiltrotor aircraft attitude control in conversion mode based on optimal preview control[C]//Guidance,Navigation and Control Conference.Piscataway,NJ:IEEE Press,2014:1544-1548.

[5] RYSDYK R T,CALISE A J.Adaptive model inversion flight control for tilt-rotor aircraft[J].Journal of Guidance,Control,and Dynamics,1999,22(3):402-407.

[6] BRICK S,FISCHER D.CV-22 osprey flight path cueing flight director system[C]//AHS Annual Forum Proceedings.Fairfax,VA:AHS,1998:251-255.

[7] KLEIN P D,NICKS C O.Flight director and approach profile development for civil tiltrotor terminal area operations[C]//AHS 54th International Annual Forum.Fairfax,VA:AHS,1998:1120-1133.

[8] CALISE A J,RYSDYK R.Research in nonlinear flight control for tiltrotor aircraft operating in the terminal area:NASA CR-203112[R].Washington,D.C.:NASA,1996.

[9] MARR R L,RODERICK W E B.Handling qualities evaluation of the XV-15 tilt rotor aircraft[J].Journal of the American Helicopter Society,1975,20(2):23-33.

[10] KIM C J,SUNG S,PARK S H,et al.Numerical timescale separation for rotorcraft nonlinear optimal control analyses[J].Journal of Guidance,Control,and Dynamics,2014,37(2):658-673.

[11] BOTTASSO C L,CROCE A,LEONELLO D,et al.Optimization of critical trajectories for rotorcraft vehicles[J].Journal of the American Helicopter Society,2005,50(2):165-177.

[12] JHEMI A A,CARLSON E B,ZHAO Y J,et al.Optimization of rotorcraft flight following engine failure[J].Journal of the American Helicopter Society,2004,49(2):117-126.

[13] CARLSON E B,ZHAO Y J.Optimal city-center takeoff operation of tiltrotor aircraft in one engine failure[J].Journal of Aerospace Engineering,2004,17(1):26-39.

[14] CARLSON E B,ZHAO Y J.Prediction of tilt-rotor height-velocity diagrams using optimal control theory[J].Journal of Aircraft,2003,40(5):896-905.

[15] CARLSON E B,ZHAO Y J.Optimal short takeoff of tiltrotor aircraft in one engine failure[J].Journal of Aircraft,2002,39(2):280-289.

[16] ZHAO Y,CARLSON E,JHEMI A,et al.Optimization of rotorcraft flight in engine failure[C]//AHS Annual Forum Proceedings.Fairfax,VA:AHS,2000:523-536.

[17] CARLSON E B,ZHAO Y J,CHEN R T N.Optimal trajectories for tiltrotor aircraft in total power failure[C]//AHS 54th International Annual Forum.Fairfax,VA:AHS,1998:1368-1380.

[18] FERGUSON S W.A mathematical model for real time flight simulation of a generic tilt rotor aircraft:NASA CR-166536[R].Washington,D.C.:NASA,1988.

[19] FERGUSON S W.Development and validation of a simulation for a generic tilt-rotor aircraft:NASA CR-166537[R].Washington,D.C.:NASA,1989.

[20] 曹蕓蕓,陳仁良.傾轉旋翼飛行器發動機短艙傾轉角度-速度包線分析[J].航空動力學報,2011,26(10):2174-2180.CAO Y Y,CHEN R L.Investigation on nacelle of conversion envelope analysis method of tiltrotor aircraft[J].Journal of Aerospace Power,2011,26(10):2174-2180(in Chinese).

[21] GILL P E,MURRAY W,SAUNDERS M A.User's guide for SNOPT version 7:Software for large-scale nonlinear programming[D].San Diego:University of California,2007:4-29.

Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft

YAN Xufei,CHEN Renliang*

National Key Laboratory of Science and Technology on Rotorcraft Aeromechanics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

The optimal control theory is applied to investigate the optimal dynamic conversion procedure of tilt-rotor aircraft to minimize the performance index described as the weighted sum of time consumed,variation of flight attitude and pilot workload.A flight dynamic model is built to extend the basic longitudinal rigid-body flight dynamic model with mixed control equations.The rates of pilot control sticks are set as the control variables to avoid jump discontinuities of controls in control strategy optimization.The dynamic conversion procedure is transformed into a dynamic optimal control problem with an appropriate performance index.The optimal control problem is formulated into a nonlinear programming problem and solved by a sparse sequential quadratic programming.XV-15 tilt-rotor aircraft is taken as the sample for the demonstration of conversion and reconversion.The results indicate that the variations of state variables are in good agreement with the data from flight simulation,and the variations of pitch attitude and pilot controls are relatively more gentle.The optimal control theory can be applied to investigate the optimal dynamic conversion procedure.

optimal control;tilt-rotor aircraft;dynamic conversion;performance index;sequential quadratic programming

2016-10-19;Revised:2016-11-25;Accepted:2017-03-02;Published online:2017-03-28 10:43

URL:www.cnki.net/kcms/detail/11.1929.V.20170328.1043.002.html

National Natural Science Foundation of China(11672128)

V212.4

A

1000-6893(2017)07-520865-11

10.7527/S1000-6893.2017.520865

2016-10-19;退修日期:2016-11-25;錄用日期:2017-03-02;網絡出版時間:2017-03-28 10:43

www.cnki.net/kcms/detail/11.1929.V.20170328.1043.002.html

國家自然科學基金(11672128)

*通訊作者.E-mail:crlae@nuaa.edu.cn

嚴旭飛,陳仁良.傾轉旋翼機動態傾轉過渡過程的操縱策略優化[J].航空學報,2017,38(7):520865.YAN X F,CHEN R L.Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft[J].Acta Aeronautica et Astronautica Sinica,2017,38(7):520865.

(責任編輯:鮑亞平,王嬌)

*Corresponding author.E-mail:crlae@nuaa.edu.cn