Clifford代數C(Λ)的E(n)-模代數結構

鄭 燁

(江蘇食品藥品職業技術學院 基礎部,江蘇 淮安 223003)

?

Clifford代數C(Λ)的E(n)-模代數結構

鄭 燁

(江蘇食品藥品職業技術學院 基礎部,江蘇 淮安 223003)

對于域k上任一個m×m矩陣Λ∈Symm(k)定義了一個Clifford代數C(Λ)，C(Λ)同構于自由代數Fm(Γ)模去某個理想I的商代數.證明了I是Fm(Γ)的E(n)-子模，由此推出C(Λ)也是一個E(n)-模代數，它的E(n)-模作用由E(n)在Fm(Γ)上的作用導出，記這樣的Clifford E(n) -模代數為C(Λ,Γ)，同時刻畫了C(Λ,Γ)的相關結構.

Clifford代數；E(n)；模代數

1 預備知識

Hopf代數是代數學的一個重要分支,起源于代數拓撲和代數群理論,它在現代代數學中有著廣泛的應用.模代數是Hopf代數中很重要的一個概念.設k是一個域，chark≠2，E(n)(n是一個正整數)是域k上的2n+1-維Hopf代數[1-2].

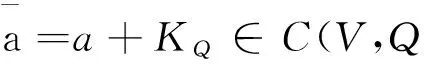
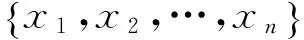
xixj+xjxi=αij，1≤i,j≤n

簡記C(V,Q)為C(M)，M=(αij)n×n稱為Clifford代數C(V)的對稱矩陣.

設Λ=(λij)m×m∈Symm(k)是數域k上的m×m對稱矩陣，則Λ確定一個Clifford代數C(Λ)，C(Λ)作為代數由x1,x2,…,xm生成，滿足關系式：

xixj+xjxi=λij，i,j=1,2,…,m.

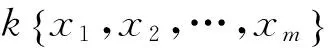
定理1[5]設Γ=(γij)n×m∈Mn×m(k)是域k上的n×m的矩陣，則Fm是一個左E(n)-模代數，其模作用由Γ確定如下：

g·xj=-xj，hi·xj=γij，1≤i≤n，1≤j≤m.

引理1[6]設A=(αij)∈Mm(k)，Fm(Γ)的代數自同態φA如上，則φA是E(n)-模同態當且僅當ΓA=Γ.

定理2[6]設A=(αij)∈Mn(k)，則φA是Fm(Γ)的E(n)-模代數自同構當且僅當A是可逆矩陣，且ΓA=Γ.

2 主要結論及其證明

定理3 設Λ=(λij)m×m∈Symm(k)是數域k上的m×m對稱矩陣，Γ=(γij)m×m∈Mm×m(k)是n×m矩陣，則C(Λ)是一個左E(n)-模代數，記作C(Λ,Γ)其模作用由下式確定：

g·xj=-xj，hi·xj=γij，1≤i≤n，1≤j≤m.

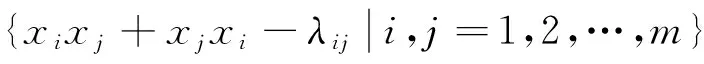
和

其中l=1,2,…,n，故ker(f)是Fm(Γ)的一個E(n)-子模，從而C(Λ)是一個左E(n)-模代數，模作用為：g·xj=-xj，hi·xj=γij，1≤i≤n，1≤j≤m.證畢.

以下我們固定一個m×m對稱矩陣Λ=(λij)和一個m×m矩陣Γ=(γij)，則自然同態f:Fm(Γ)→C(Λ)，xjаxj是一個E(n)-模代數同態.任取域k上的一個m×m矩陣A=(αij)，則A確定了Fm(Γ)唯一的一個代數自同態φA.此時C(Λ,Γ)的一個線性變換

ψA:C(Λ,Γ)→C(Λ,Γ)

稱為由φA誘導的，如以下交換:

↓f ↓f

注意，若這樣的ψA存在，必是由φA唯一確定的.

引理2 設A=(αij)∈Mm(k)，則φA可誘導出C(Λ,Γ)的一個代數自同態ψA的充分必要條件是ATΛA=Λ，此時

證明 眾所周知φA能誘導出C(Λ,Γ)的一個代數自同態的充分必要條件是φA(ker(f))?ker(f).下面在Fm(Γ)中計算，對任意的1≤i,j≤m，有

φA(xixj+xjxi-λij)=

φA(xixj)+φA(xjxi)-φA(λij)=

φA(xi)φA(xj)+φA(xj)φA(xi)-λij=

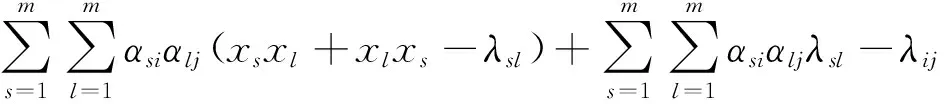
因此

φAker(f)?ker(f)?φA(xixj+xjxi-λij)∈

ker(f),?1≤i,j≤m

進一步地，若φA誘導的ψA存在，則對任意的1≤i≤m，有

ψA(xi)=ψA(f(xi))=(ψAf)(xi)=

設A=(αij)∈Mm(k)，且φA可誘導出C(Λ,Γ)的一個代數自同態ψA，由引理2和引理1可得出ψA是E(n)-模同態的充分必要條件是ΓA=Γ.進一步可以得到φA可誘導出C(Λ,Γ)的一個E(n)-模代數自同態ψA的充分必要條件是ATΛA=Λ且ΓA=Γ.

引理3 設A=(αij)∈Mm(k)，且φA可誘導出C(Λ,Γ)的一個代數自同態ψA，則ψA是代數自同構的的充分必要條件是A為可逆矩陣.

證明 由引理2和假設條件知ATΛA=Λ.

設A是可逆矩陣，則由定理2的證明知φA可逆且φA-1=φA-1.因為ATΛA=Λ，所以(A-1)TΛA-1=Λ，再由引理3知φA-1可誘導出C(Λ,Γ)的一個代數自同態ψA-1，進一步地還有ψAψA-1=ψA-1ψA=id，故ψA是C(Λ,Γ)的代數自同構.

反之，假設ψA是C(Λ,Γ)的代數自同構.令

V=span{x1,x2,…,xm}

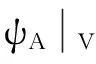
[1]BEATTIEM,DSCLESCUS,GRüNENFELDERL.ConstructingpointedHopfalgebrasbyOreextension[J].J.Algebra, 2000, 225:743-770.

[2]CARNOVALEG,CUADRAJ.CocycletwistingofE(n)-modulealgebrasandapplicationstotheBrauergroup[J].K-Theory, 2004, 33:251-276.

[3]ZHANGY,CHENHX,HONGHB.StructuretheoremsofE(n)-azumayaalgebras[J].Front.Math.China, 2010, 5:757-776 .

[4]PERTTIL.CliffordAlgebrasandSpinors[M].Cambridge:CambridgeUniversityPress, 2001.

[5]鄭燁.自由代數Fm的E(n)-模代數的證明[J].山東理工大學學報(自然科學版)，2014，28(6)：59-61.

[6]鄭燁.自由代數Fm的E(n)-模代數結構的研究[J].山東師范大學學報(自然科學版)，2015(3)：63-64.

(編輯：郝秀清)

Research ofE(n)- module algebra structure of the Clifford algebraC(Λ)

ZHENG Ye

(Department of Basic Course,Jiangsu Food and Pharmaceutica Science College,Huai′an 223003,China)

For a m×m and matrix Λ∈Symm(k) of field k， we defines a Clifford algebraC(Λ)，whichisisomorphictoafreealgebraicFm(Γ)modeltheidealIquotient.Firstly,weprovedthatIisFm(Γ)E (n) -submodule,thenconcludedthatC(Λ)isanE (n) -modelalgebra,whoseE (n) -modelactionisderivedfromtheFm(Γ)-model,here,wedenoteCliffordE (n) -modelalgebrabyC(Λ,Γ).AtthesametimewedescribedtherelatedstructureofC(Λ,Γ).

Cliffordalgebra；E (n)；modelalgebra

2016-03-17

鄭燁,女,zhengyee@126.com

1672-6197(2017)01-0076-03

O153.3

A