新一代運載火箭適應發動機停擺故障控制策略研究
馮 昊 李新明 潘 豪
北京航天自動控制研究所, 北京100854
新一代運載火箭適應發動機停擺故障控制策略研究
馮 昊 李新明 潘 豪
北京航天自動控制研究所, 北京100854
我國新一代運載火箭采用了助推發動機與芯級發動機聯合搖擺控制模式,但隨著參與控制發動機數量的增加也帶來了控制系統可靠性降低的風險。本文針對火箭飛行過程中發生的單臺發動機停擺故障,從控制力補償原理進行分析,提出了控制力補償策略,并進一步對發動機停擺可適應的能力范圍進行了研究,最后通過數學仿真得到驗證。應用該控制策略可以實現新一代運載火箭發動機的故障吸收,提高系統的可靠性。
控制力補償;故障吸收;發動機故障;可靠性
運載火箭是實施太空發展戰略的基礎,為了保證新一代運載火箭的運載能力和控制能力,新一代運載火箭的助推發動機不同于我國現有捆綁助推器的發動機噴管固定不擺動的形式,而是采用和芯級發動機相類似的單向甚至多向擺動以控制火箭的飛行方向,新型火箭的控制系統也隨之從單純的芯級擺動發動機穩定控制轉化成更為復雜的芯級與助推級多臺發動機同時擺動的協調控制。
隨著參與控制發動機數量的增加,火箭飛行控制的復雜程度增大。本文研究了發動機存在伺服機構故障時控制力重新分配的算法,即當火箭飛行過程中發生單臺發動機停擺故障時,設計控制力補償策略,即保證發動機故障前后的系統控制力和控制力矩保持恒定[1-2]。通過該策略可以實現火箭發動機的故障吸收,提高系統的可靠性。
1 控制力補償原理
發動機發生故障后,力矩平衡遭到破壞,運載火箭姿態發生變化,要使運載火箭能夠穩定飛行,必須保證滾轉角為0,即通過控制力補償策略來實現發動機故障吸收。主要通過正常發動機擺角的擺動抵消因為停擺產生的附加力矩來改變控制律,重新分布各發動機的力和力矩,使最終產生的控制力矩保持不變,即等于發動機均正常工作時產生的控制力矩。以某新型運載火箭為例,一級發動機尾視圖如圖1所示。
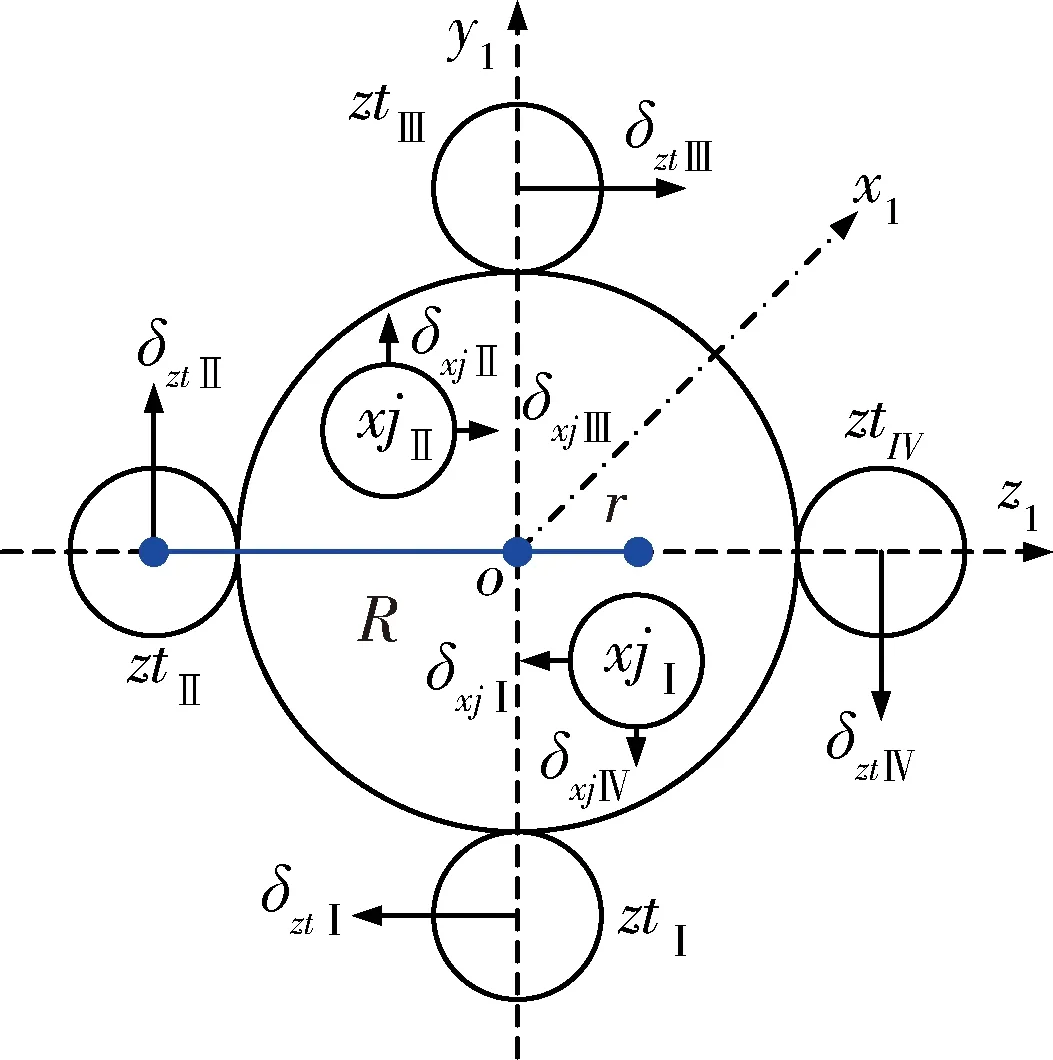
圖1 一級發動機尾視圖
假設助推發動機舵擺角分別為:δztⅠ,δztⅡ,δztⅢ,δztⅣ,各臺助推發動機推力為Nzt。芯級發動機舵擺角分別為:δxjⅠ,δxjⅡ,δxjⅢ,δxjⅣ,各臺芯級發動機推力為Nxj。火箭擺動軸到火箭質心的距離為L,火箭擺動軸到火箭縱軸距離分別為R和r。這里設Nzt=Nxj,R=mr,可以得到俯仰、偏航和滾轉三通道[2]的控制力矩。一般情況下,各擺角擺動的度數不大,近似認為sinδzt≈δzt, sinδxj≈δxj。
滾轉控制力矩:
Mxc=Nzt(δztⅠ+δztⅡ+δztⅢ+δztⅣ)R+Nxj(δxjⅠ+δxjⅡ+δxjⅢ+δxjⅣ)r
(1)
偏航控制力矩:
Myc=[Nzt(δztⅠ-δztⅢ)+Nxj(δxjⅠ-δxjⅢ)]L
(2)
俯仰控制力矩:
Mzc=[Nzt(δztⅣ-δztⅡ)+Nxj(δxjⅣ-δxjⅡ)]L
(3)
當發動機停擺之后,若使發動機產生控制力矩保持不變,需要對其它發動機舵擺角進行重新分配,來保證俯仰、偏航和滾轉3通道的控制力矩重新達到平衡。
2 控制力補償策略
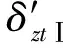
根據力矩平衡[3]原理,要使故障發生前后的控制力矩保持不變,必須滿足下式:
(4)
由于助推發動機Ⅱ停擺,此擺角只影響俯仰角和滾轉角,不影響偏航通道。因此控制偏航通道的發動機擺角不受影響。
(5)
設助推發動機相對火箭中心軸的距離R與芯級發動機相對火箭中心軸的距離r滿足一定的關系式,即R=mr。化簡上述方程得到:
(6)
并令:
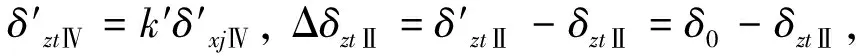
得到助推發動機II停擺時,其它正常工作相關發動機擺角為:
(7)
式(7)即適應發動機停擺故障所采用的控制力補償算法,其中,m為助推發動機相對火箭中心軸的距離R與芯級發動機相對火箭中心軸的距離r之比,為火箭的固有結構系數。k和k′為故障前后助推發動機和芯級發動機擺角關聯系數,屬于可調整系數。
發生故障后,助推級各發動機擺角與芯級各發動機擺角會發生變化。經過分析,此倍數關系取太小,則造成發生故障后的其它發動機擺角會過大,有可能超過所給限幅值;取太大,則停擺的角度范圍會過小,具體可根據實際情況調整。
3 故障可適應能力分析
同樣,考慮助推發動機Ⅱ(δztⅡ)發生停擺故障,討論發動機停擺范圍問題。
根據式(7)的重構策略,且δztⅠ(Ⅰ,Ⅱ,Ⅲ,Ⅳ)=kδxjⅠ(Ⅰ,Ⅱ,Ⅲ,Ⅳ),可得擺角差值關系式組:
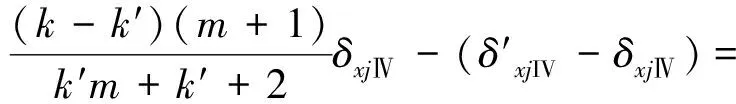
(8)
分析上述參數,由于k,k′為故障前后助推發動機和芯級發動機作用擺角之比,而當助推發動機停擺時,應該適當加大芯級發動機的作用力,應滿足0lt;k′≤k。另外,參數m為助推發動機和芯級發動機控制力臂長度之比,且mgt;1恒成立,有如下關系:
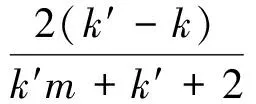
(9)
且:
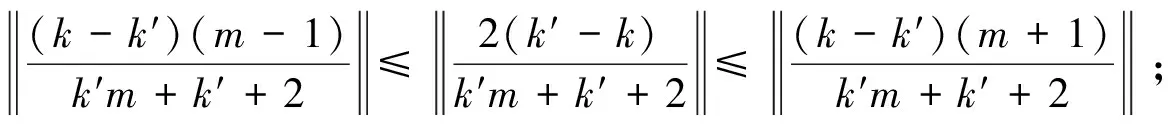
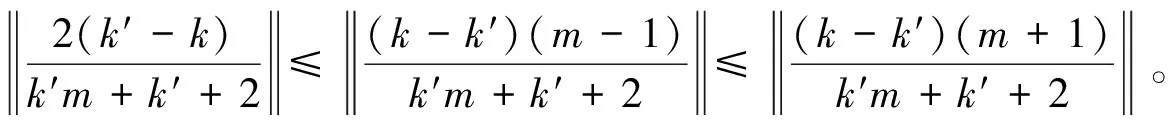
易得:
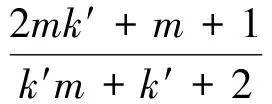
因此當助推發動機Ⅱ停擺,m不太大時,其對應的芯級發動機Ⅱ(δxjⅡ)受其影響較大,與本文第4節中的數學仿真結論相符(如圖2~3)。因此,可以根據芯級發動機Ⅱ的限制角度反推得到助推發動機Ⅱ的停擺范圍,即停擺故障可適應能力。
可以得出芯級發動機Ⅱ的擺角分配策略:
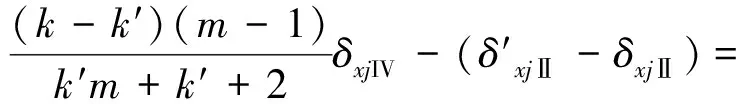
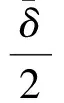
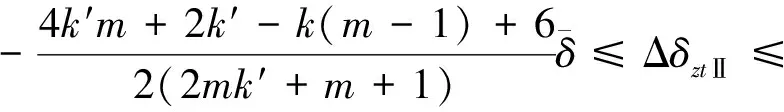
(10)
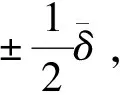
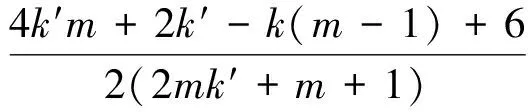
(11)

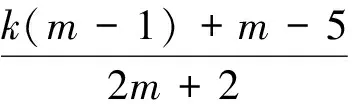
4 數學仿真及結果分析
為驗證本文給出的發動機故障情況下控制力補償策略的有效性,進行了數學仿真研究。仿真中以助推級發動機Ⅱ分機發生停擺故障為例,仿真條件取發生故障后,助推級各發動機擺角與芯級各發動機擺角的倍數關系為0.8,即k′=0.8,取m=5.5。
助推級發動機Ⅱ分機在20s時發生故障,俯仰通道、偏航通道和滾動通道的姿態角偏差仿真曲線分別如圖2~4。圖中,“……”曲線為發動機無故障仿真曲線,“——”曲線為發動機故障但是未采取控制力補償策略仿真曲線,“-·-·-”曲線為發動機故障且采用了本文的控制力補償策略仿真曲線。
采用控制力補償策略后的助推發動機擺角曲線和芯級發動機擺角曲線分別如圖5和6。
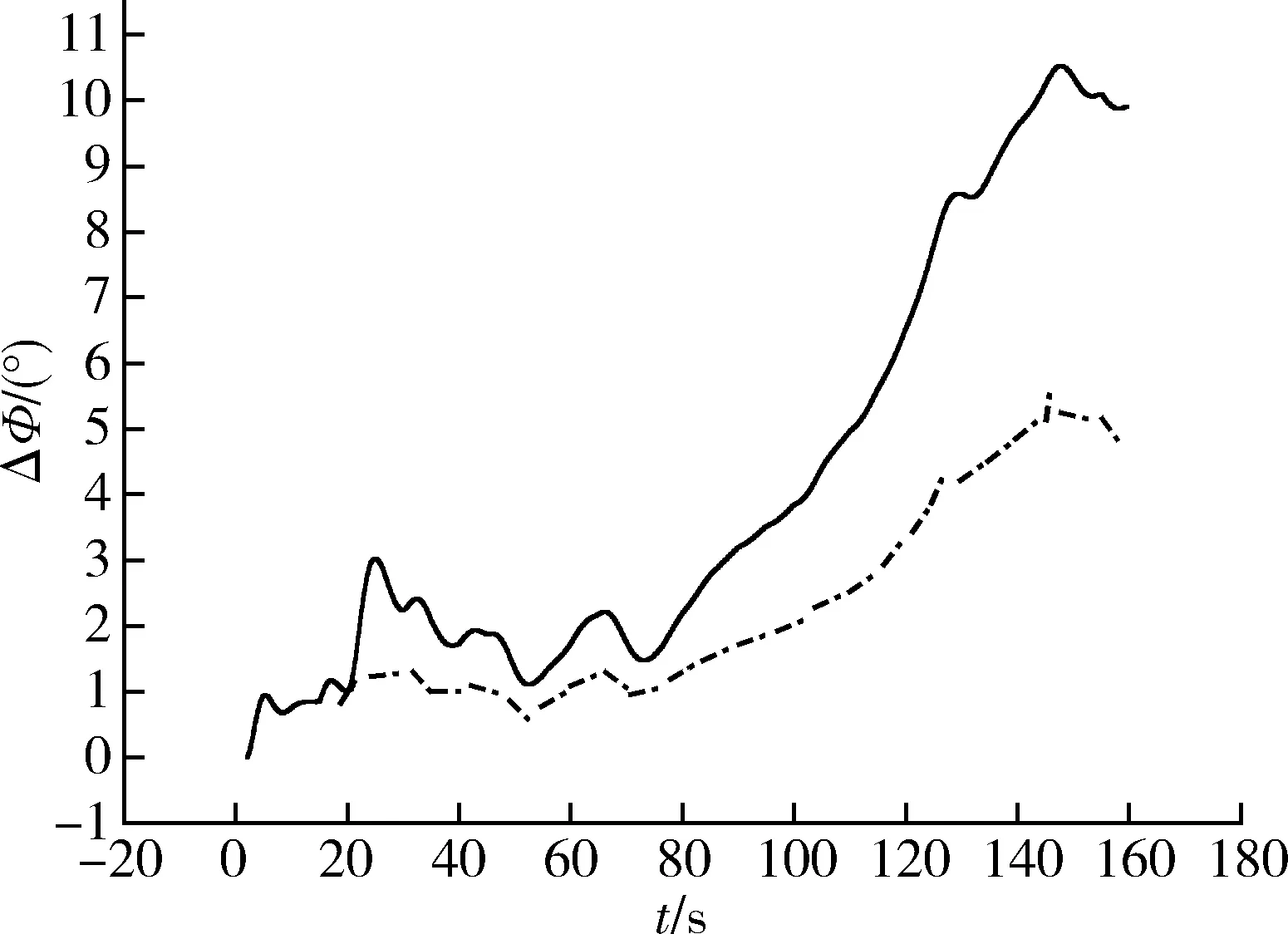
圖2 助推級發動機II分機故障時俯仰姿態角偏差ΔΦ仿真曲線
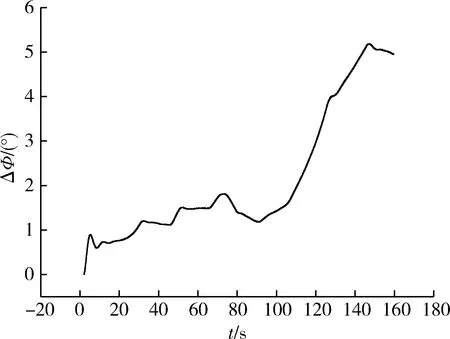
圖3 助推級發動機II分機故障時偏航姿態角偏差ΔΨ仿真曲線
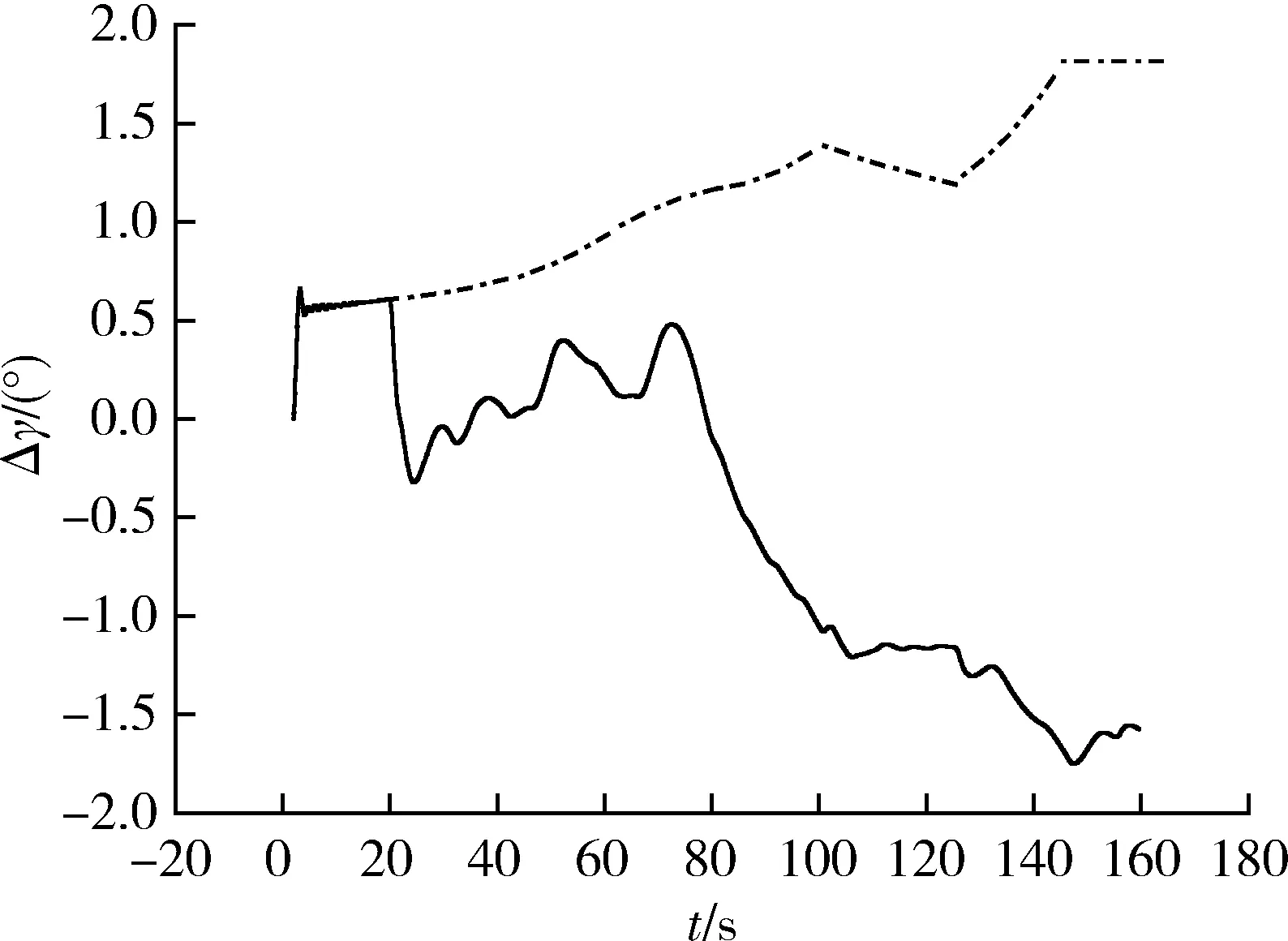
圖4 助推級發動機II分機故障時滾動姿態角偏差Δγ仿真曲線
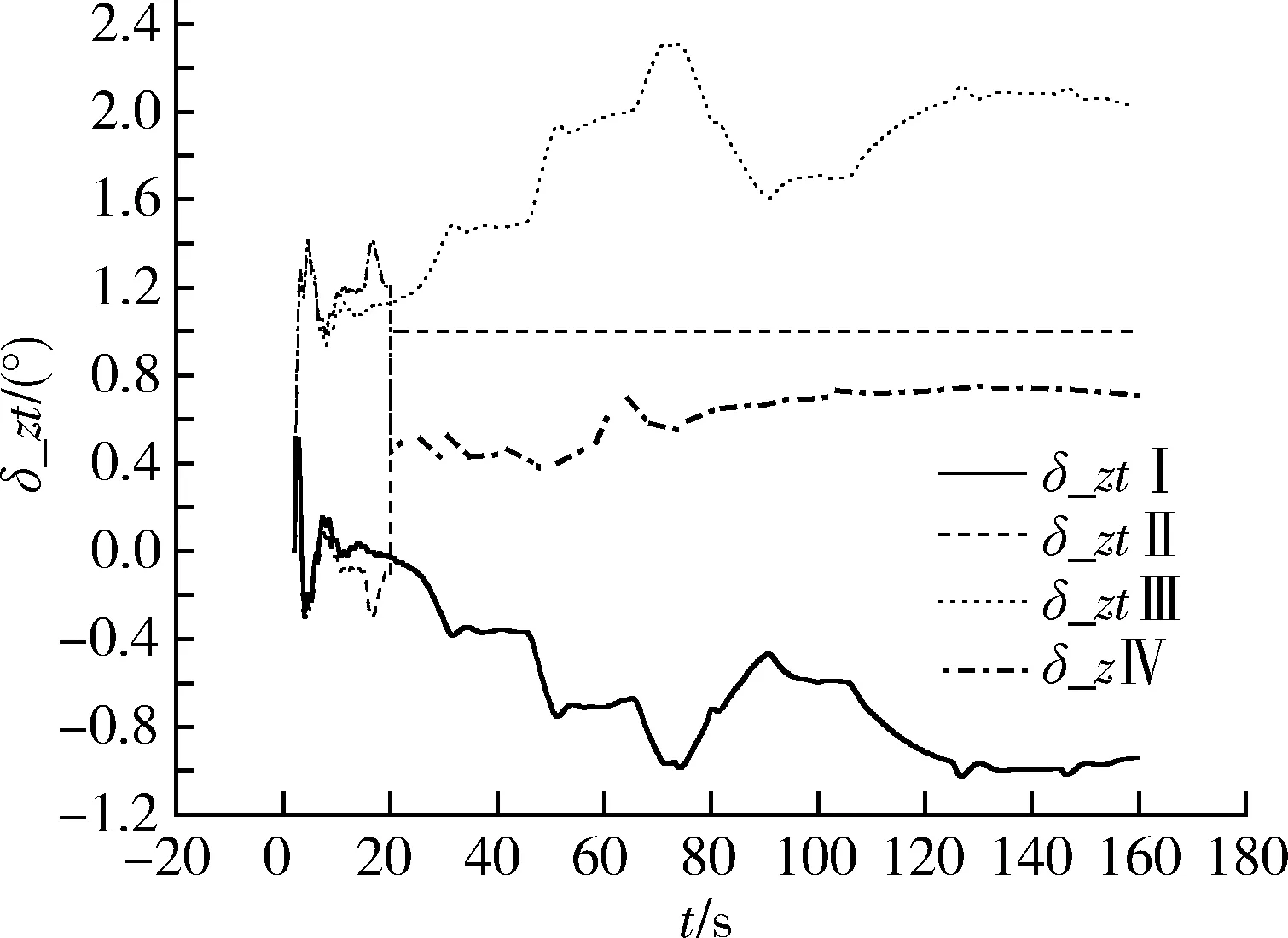
圖5 助推級發動機II分機故障時助推發動機擺角仿真曲線
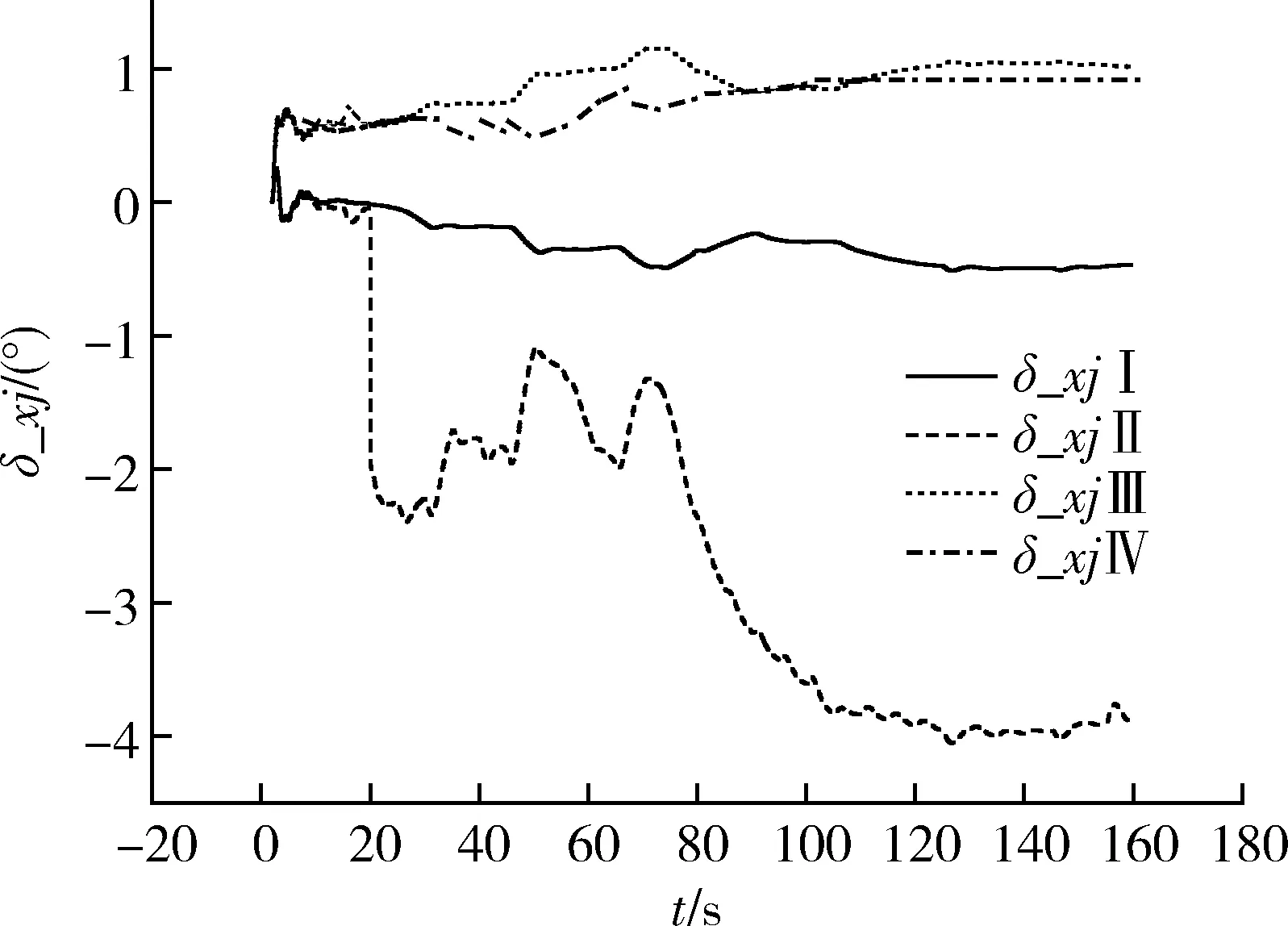
圖6 助推級發動機II分機故障時芯一級發動機擺角仿真曲線
以上仿真證明,當火箭飛行過程中出現一臺發動機停擺后,經過控制力補償,且當各個發動機的擺角小于給定的限幅值時,姿態角能夠實現很好的跟蹤效果,消除發動機停擺故障對控制系統的影響。
5 結論
控制力補償策略是控制系統提高可靠性的有效手段。本文針對運載火箭發動機停擺故障,通過理論推導提出了實現火箭控制力補償的策略方法,并進一步研究得到了發動機故障可適應的能力范圍,采用控制力補償有效的提高了發動機故障情況下的控制品質。分析和仿真結果表明,應用該策略在控制系統出現發動機停擺故障后,姿態角和姿態角速度變化平緩,控制精度較好。可以實現新一代運載火箭發動機的故障吸收,從而提高了系統的可靠性。
[1] 徐延萬,等.液體彈道導彈與運載火箭系列[M].控制系統(上).北京:宇航出版社,1989.(Xu Yanwan, et al. Liquid Ballistic Missile and Launch Vehicle Series[M].Control System(part I).Beijing:Aerospace Press, 1989.)
[2] 徐延萬,等.液體彈道導彈與運載火箭系列[M].控制系統(下).北京:宇航出版社,1989. (Xu Yanwan, et al. Liquid Ballistic Missile and Launch Vehicle Series[M]. Control System (part II). Beijing:Aerospace Press, 1989.)
[3] 胡壽松. 自動控制原理[M].北京:國防工業出版社,1994. (Hu Shousong.Automatic Control Principle[M]. Beijing:National Defense Industry Press, 1994.)
ResearchonControlStrategyofNewGenerationLaunchVehiclesAdaptiontoEngineFault
Feng Hao, Li Xinming, Pan Hao
Beijing Aerospace Automatic Control Institute, Beijing 100854,China
Thejointswingcontroltechnologyoftheboosterengineandthecoreengineisemployedinthenewgenerationlaunchvehicles.Butwiththeincreasingnumberofcontrolengine,theriskofreducingthereliabilityofthecontrolsystemisalsobrought.Accordingtotheprincipleofcontrolforcecompensation,inthispaper,asingleenginefailureoccurredduringflightisstudiedandthecontrolstrategyisproposed.Andfurthertheabilityrageofenginefaultcanbestudied.Finally,thecontrolstrategyisverifiedbymathematicalsimulation.Applicaitonofthiscontrolstrategycanrealizethefaultabsorptionoftheengineandimprovethereliabilityofthecontrolsystem.
Controlforcecompensation;Faultabsorption;Enginefault;Reliability

V448.22
A
1006-3242(2017)04-0057-05
2016-11-29
馮昊(1976-),女,遼寧人,碩士,高級工程師,主要研究方向為導航、制導與控制;李新明(1976-),男,河北人,碩士,高級工程師,主要研究方向為導航、制導與控制;潘豪(1981-),男,山東人,博士,高級工程師,主要研究方向為導航、制導與控制。

