函數知識中的誤區警示

■陜西洋縣中學 劉大鳴(特級教師)

函數知識中的誤區警示

■陜西洋縣中學 劉大鳴(特級教師)

本文匯集了函數的概念及性質 、二次函數、冪函數、指數函數、對數函數、函數與方程等知識中的易錯題,剖析了出錯的原因,給出了警示和易錯點,希望能引起同學們的高度重視。

一、函數概念和性質應用中的誤區警示

誤區1——判斷函數奇偶性時忽略定義域

從而可知函數f(x)為非奇非偶函數。

剖析:錯解中只注意了f(-x)=±f(x)的探究,忽略了函數定義域的研究,由題意知自變量x滿足即函數的定義域為(-1,0)∪(0,1),定義域關于原點對稱,在定義域下化簡f(x)=易證f(-x)=-f(x),即函數為奇函數。

警示:與函數有關的問題必須遵循“定義域優先”的原則,研究函數的奇偶性,先求函數的定義域,在定義域關于原點對稱的前提下,實施數學式子f(-x)=±f(x)的變形進行探究。

跟蹤訓練1 函數f(x)=l g(x+1)+l g(x-1)的奇偶性是( )。

A.奇函數 B.偶函數

C.非奇非偶函數 D .既奇又偶函數

易錯點:忽略函數的定義域。

誤區2——研究分式類函數的單調性時缺少分類意識例2 函數f(x)=x在(2,+∞)上x+a為減函數,則a的取值范圍是____。

易錯點:缺少分式類函數單調性的逆用。

誤區3——抽象函數單調性證明中以特殊代替一般推理

例3 若函數f(x)對于任意x,y∈R,總有f(x)+f(y)=f(x+y),且當x＞0時,f(x)＜0,f(1)=-,求證:f(x)在R上是減函數。

錯解:令x=y=0,則2f(0)=f(0),所以f(0)=0。再令x=-1,y=1,則有f(-1)+f(1)=f(0)=0。又f(1)=-2,3

剖析:減函數的定義:對于定義域的子區間中的任意兩個自變量x1,x2,當x1＜x2時,有f(x1)＞f(x2),不能取兩個特殊值代替。設x1＞x2,則f(x1)-f(x2)=f(x1-x2+x2)+f(x2)=f(x1-x2)+f(x2)-f(x2)=f(x1-x2)。因為x＞0,f(x)＜0,而x1-x2＞0,所以f(x1-x2)＜0,即f(x1)＜f(x2),因此f(x)在R上是減函數。

警示:證明或判斷函數的單調性要從定義出發,作差后要注意差式的分解變形,合理使用其他題設條件,x＞0時f(x)＜1,我們由x2＞x1,得到x2-x1＞0,則f(x1-x2)＜1,然后要尋找其與f(x2)-f(x1)＞0的關系,所以要進行配湊。

跟蹤訓練3 定義在R上的恒為正數的函數f(x),當x＞0時,f(x)＞1,對任意x,y∈R,都有f(x+y)=f(x)f(y),證明函數f(x)為增函數。

易錯點:忽略定義法證明推理中的合理變形。

正解:任取x1,x2∈R,x1＜x2,則x2-x1＞0。因為當x＞0時,f(x)＞1,所以f(x2-x1)＞ 1。 而f(x2-x1)＞1,又f(x1)＞0,所以f(x2)＞f(x1),所以函數f(x)為R上的增函數。

誤區4——分段函數不等式求解忽略分類或每段的前提條件

警示:分段函數不等式求解,利用分類討論思想,關鍵在于“對號入座”,即分段函數中自變量取值范圍的界定,代入相應的解析式求解不等式,注意取值范圍的大前提,然后把兩個不等式的解集并起來即可。

易錯點:分段函數不等式求解忽略分類或每段的前提條件。

正解:因為x2≥0,所以f (x2)=x2。

因為f(x2)＞f(4-3x),所以x2＞4-3x,即x＜-4或x＞1,所以x＜-4或1＜x

二、二次函數和冪函數中的誤區警示

誤區5——形如二次函數的函數忽略二次項的系數為0的討論

例5 如果函數f(x)=(a-2)x2+2(a-2)x-4的圖像恒在x軸下方,試求實數a的取值范圍。

錯解:要使函數f(x)的圖像恒在x軸下方,只要拋物線開口向下,與x軸無交點,所解得-2＜a＜2。因此實數a的取值范圍為(-2,2)。

剖析:錯解忽略二次項的系數為0的討論,誤認為f(x)=(a-2)x2+2(a-2)x-4為二次函數,此題在a=2時,f(x)=-4,圖像也恒在x軸下方,滿足題意,結合錯解知實數a的取值范圍是(-2,2]。

警示:在形如二次函數y=a x2+b x+c中,當a≠0時為二次函數,其圖像為拋物線;當a=0,b≠0時為一次函數,其圖像為直線。在處理此類問題時,應密切注意x2項的系數是否為0,若不能確定,應分類討論。

跟蹤訓練5 函數f(x)=(m-1)x2+2(m+1)x-1的圖像與x軸只有一個交點,求實數m的取值范圍。

易錯點:忽略二次項的系數為0的討論

正解:(1)當m-1=0,即m=1時,f(x)=4x-1與x軸只有一個交點,滿足題意。

(2)當m-1≠0,即m≠1時,Δ=4(m+1)2-4×(-1 0)×(m-1)=0,解得m=0或m=-3。

誤區6——二次函數最值問題未對對稱軸和區間的位置討論

例6 求函數f(x)=x2-4a x+1在區間[0,2]上的最大值和最小值。

錯解:當x=0時,f(x)取得最小值f(0)=1;當x=2時,f(x)取得最大值。

剖析:因為函數的對稱軸不確定,故需討論對稱軸與區間[0,2]的關系,并結合二次函數的單調性來解決問題。

(1)當2a＜0,即a＜0時,f(x)的圖像開口向上,故f(x)在 0,2[ ]上遞增,故有f(x)max=f2()=5-8a,f(x)min=f0()=1。(2)當0＜2a＜1,即0＜a＜時,f(x)的圖像開口向上,故f(x)在 [0 ,2a]上遞減,在 [2 a ,2]上遞增,故有f(x)max=f(2)=5-8a,f(x)min=f(2a)=1-4a2。

的圖像開口向上,故f(x)在區間[0,2a]上遞減,在[2a,2]上遞增,故有當x=2a時,f(x)取得最小值f(2a)=1-4a2;當x=0時,f(x)取得最大值f(0)=1。

(4)當2a＞2,即a＞1時,f(x)的圖像開口向上,故f(x)在區間[0,2]上遞減,故有x=0時,f(x)取得最大值f(0)=1;當x=2時,f(x)取得最小值f(2)=5-8a。

警示:二次函數在閉區間上的最值主要有三種類型:軸定區間定、軸動區間定、軸定區間動。不論哪種類型,解題的關鍵是對稱軸與區間的關系,當含有參數時,要依據對稱軸與區間的關系進行分類討論。最值一般在區間的端點或頂點處取得。

跟蹤訓練6 如果函數f(x)=(x-1)2+1定義在區間t,t+1[ ]上,求f(x)的最小值。

易錯點:求二次函數最值問題未對對稱軸和區間的位置討論。

正解:函數f(x)圖像的對稱軸為x=1。

(1)當t+1＜1,即t＜0時,f(x)min=f(t+1)=t2+1;

(2)當t＞1時,f(x)min=f(t)=t2-2t+2。

(3)當t≤1≤t+1,即0≤t≤1時,f(x)min=f(1)=1。

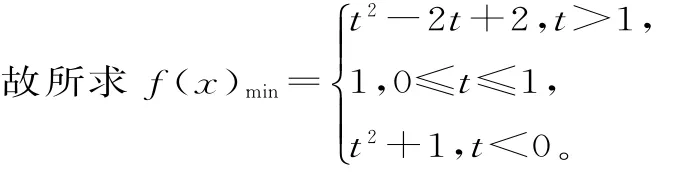
誤區7——隨意用判別式研究二次方程根的分布問題

例7 求方程f(x)=a x2+b x+c=0(a＞0)的兩個根都大于1的等價條件。

錯解:只要方程f(x)=a x2+b x+c=0(a＞0)對應的二次函數為f(x)=a x2+b x+c的圖像與x軸交點的橫坐標都大于1即可,故需滿足所以充要條件是

剖析:上述解法中,只考慮到二次函數與x軸交點坐標要大于1,卻忽視了最基本的前提條件,應讓二次函數的圖像與x軸有交點才行,即滿足Δ≥0,故等價條件是

警示:等價轉化是數學的重要思想方法之一,處理得當會收到意想不到的效果,但等價轉化的前提是轉化的等價性,反之會出現各種離奇的錯誤。

跟蹤訓練7 已知方程有且只有一個根在區間(0,1)內,那么實數m的取值范圍為____。

易錯點:隨意用判別式研究二次方程根的分布問題。

正解:因為方程m x2-3x+1=0有且只有一個根在區間(0,1)內,所以函數y=m x2-3x+1的圖像與x軸在(0,1)內有且只有一個交點,所以f(0)f(1)＜0或Δ=0,解得m＜2且m=

誤區8——冪函數單調性應用中缺少分類

例8 若(m+1)4＜(3-2m)4,試求實數m的取值范圍。

錯解:由(m+1)4＜(3-2m)4和冪函數性質知,m+1＜3-2m,所以m＜。

剖析:錯解中誤認為m+1,3-2m都在[0,+∞)內,y=x4在[0,+∞)上單調遞增導致漏解。此不等式可分類求解,若注意y=x4的圖像關于y軸對稱的特點,利用絕對值將問題轉化為y=x4在(0,+∞)上的單調性問題可尋求簡潔的思路。由冪函數y=x4的圖像知此函數在(-∞,0)和(0,+∞)上不具有單調性,若分類討論步驟較繁,把問題轉化到一個單調區間上是關鍵。考慮當冪函數的指數為4時,于是有(m+1)4＜(3-2m)4

又因為冪函數y=x4在(0,+∞)上單調遞增,所以解得m＜,或m＞4。

警示:研究冪函數時,先研究定義域,再利用對稱性和單調性簡化求解問題。本題巧妙運用轉化思想解題,從而避免了分類討論,使同學們的思維又一次得到深化與發展。解題過程中利用圖像關于y軸對稱的特點,將函數不等式轉化為含絕對值不等式的解法,蘊含的這種“轉化”的思想,一方面,拓寬了我們的解題思路,另一方面,體現了對知識的靈活應用能力。當然此題還可用分類討論的方法解決,同學們不妨一試。

跟蹤訓練8 若(m+1)-1＜(3-2m)-1,則實數m的取值范圍為____。

易錯點:冪函數單調性應用中缺少分類。

(3)兩個整體變量分別在(-∞,0)和(0,+∞)上,由圖像知解得m＜-1。

三、指數和對數函數中的誤區警示

誤區9——換元法中忽視指數函數在區間上的值域

例9 函數f(x)=4x+2x+1+2(x≤0)的值域是____。

錯解:f(x)=4x+2x+1+2=(2x)2+2·2x+2,令t=2x,則t＞0,且y=t2+2t+2=(t+1)2+1,當t∈(-1,+∞)時,f(t)是增函數,而t＞0,所以(0+1)2+1＜y,即2＜y。所以所求函數f(x)的值域為(2,+∞)。

剖析:利用4x=(2x)2的關系,不難想到本題中要將2x當作一個整體進行換元,轉化得到一個新的一元二次函數,新的參數的取值范圍縮小導致值域出錯。

f(x)=4x+2x+1+2=(2x)2+2·2x+2(x＜0),令t=2x,則0＜t≤1,且y=t2+2t+2=(t+1)2+1,當t∈(-1,+∞)時,f(t)是增函數,而0＜t≤1,所以(0+1)2+1＜y≤(1+1)2+1,即2＜y≤5。所以所求函數f(x)的值域為(2,5]。

警示:在利用換元法求函數值域、最值時,經過換元,函數的定義域可能會發生變化。在運用換元法時,一定要注意換元后函數定義域為新變量對原變量的值域。

易錯點:換元法中忽視指數函數在區間上的值域。

誤區1 0——求對數的復合函數的單調區間忽視定義域

例1 0 函數y=l o g0.5(4+3x-x2)的單調遞增區間是____。

錯解1:因為外層函數為減函數,內層函數u=4+3x-x2的減區間為以原函數的增區間為

錯解2:因為4+3x-x2＞0,函數定義域為 (- 1,4),又內層函數u=4+3x-x2在上為增函數,在函數,所以原函數的增區間為

剖析:錯解1,忽視定義域問題;錯解2,對復合函數單調性法則不熟練。

因為4+3x-x2＞0,函數定義域為(- 1,4),外層函數為減函數,內層函數u=4+3x-x2在上為增函數,在上為減函數,所以原函數的增區間為

警示:復合函數的單調區間,先求出它的定義域,再根據復合函數“同增異減”在定義域內確定其子區間。

跟蹤訓練1 0 函數f(x)=l n(4+3xx2)的單調遞減區間是____。

易錯點:求對數函數的單調性時忽略定義域。

正解:函數f(x)=l n(4+3x-x2)的定義域是(-1,4),令u(x)=-x2+3x+4=,其減區間為e＞1,所以函數f(x)的單調減區間為[2 3,4)。

(責任編輯 王福華)