追求適合有深度的數學教學

■龐彥福

追求適合有深度的數學教學

■龐彥福

《國家中長期教育改革和發展規劃綱要》（2010—2020年）指出：“尊重教育規律和學生身心發展規律，為每個學生提供適合的教育。”適合的教育才是最好的教育，同樣，適合的教學也才是最好的教學。學生是有差異的，面對不同層次的學生，設計并實施怎樣的教學才能適合學生的學習，利于學生的成長，促進學生的發展，是有責任心的教育工作者及一線教師需要不斷思考的課題。

一、適合的教學需尊重學生

“九層之臺，起于壘土。”教學應以學生為主體，立足學生的學，有助于學生的成長和發展。奧蘇貝爾曾在他的《教育心理學：認知的觀點》一書中寫道：“假如讓我把全部教育心理學僅僅歸結為一條原理的話，那么，我將一言以蔽之：影響學習的唯一重要的因素就是學習者已經知道了什么。要探明這一點，并據此進行教學。”學生學習數學是建立在已有知識及其經驗之上的。在“分式”教學時，筆者曾這樣設計新課的引入：

之所以這樣設計新課的引入，主要是基于以下幾點考慮。首先，易切入，好上手。凡事從簡單做起。我國古代著名哲學家、思想家老子有句名言：“天下難事，必做于易；天下大事，必做于細。”它精辟地指出想成就一番事業，必須從簡單的事情做起，從細微之處入手。以最簡單的小學知識“作為新課引入的切口，盡管起點低，但是立意高，這樣學生可以通過聯想類比學習新知識，易于將分數的相關知識遷移到新知識的學習上來。其次，回歸和體現數學的本質。從“1÷2”到“1÷2x”、從回顧了分數的產生和意義，也喚醒學生了解從“分數”到“分式”、從“整式”到“分式”的過渡過程，從而讓學生體悟知識間的互相聯系以及學習分式的基本方法。第三，學生感覺到親切自然。新課引入的問題情境并沒有刻意進行“創設”，四個小問題貼近生活實際，貼近學生的生活。無論是從分數到分式的過渡，還是老師上班的實例，既接地氣，又讓學生體會到數學就在自己身邊。第四，滲透整體架構的意識，有利于建立起邏輯連貫的知識體系和學習過程。數學體系是一脈相承的，有了整體化的設計思想，對于整個的教學設計就會有全局的考慮。第五，滲透研究數學概念的一般套路和方法。設計的5個小問題，是先給出例子，并讓學生根據例子寫出式子，然后通過觀察、探尋來發現它們的共同屬性。這樣得到的分式定義才是學生自己習得的，如此的設計與學習過程才符合概念形成的規律。有了前面的鋪墊和基礎，到了學生自己舉例子、概念辨析以及新知識的應用等環節，學生便會自主進入有深度的探究之中。這樣的設計，學生習得知識的過程才符合深度學習的特征。第六，將隱性知識與顯性知識有機結合。從特殊到一般、從具體到抽象以及類比的思想方法，融入到了新課的情境問題之中（如圖1）。有了分式概念的深度探究，接下來學習分式的性質、運算及應用就有了堅實的基礎以及可類比的基本方法。

圖1

二、適合的教學需因材施教

教學中，教師如果對學習薄弱的學生采取的方法不當，薄弱生就會變成學困生，甚至跟不上課，只會越來越差。一個學生或個別學生在班級里或學校里只是集體中的一員，而對于家庭來說，他則可能是全部。因此，教育應該對每一個學生負責。

小K同學由于基礎不好，學習起來相對困難，下面是小K作業中出現的錯誤：（1）25的平方根是

老師并沒有在小K作業錯誤的地方打上大大的“×”或留下其他傷害性的標記，而是利用課外時間找到小K了解情況：

小K：結果是一樣的，表示形式不同。

教師：結果是多少，怎樣表示呢？

教師：我們逆過來想，平方等于36的數是幾……

經過老師和同學的幫助，小K的學習有了明顯的進步。

蘇霍姆林基說過：“在人的心靈深處，都有一種根深蒂固的需要，這就是希望自己是一個發現者、研究者、探索者。而在兒童的精神世界中，這種需要則特別強烈。”我們常說網絡是雙刃劍，其實，教學中的評價也可能是雙刃劍，既能發揮積極作用，也會產生消極影響。老師對小K的錯誤沒有打上大大的“×”號，沒有批評她“這么簡單的題目都不會”，沒有直接教她“訂正”，而是從類似的題目入手，讓她理解知識、明白道理、尋找方法。一個“×”號看上去是客觀的，但也是一種傷害；一句不經意的“這么簡單的題目都不會”，從老師嘴里說出是那么的輕巧，可殺傷力是巨大的，在學生的內心深處可能會留下“我就是笨孩子”“我就是學不會”的烙印。在“的平方根是多少”的問題中，小K等同學為什么會得出的結論？其實是沒有真正理解非負數的平方根，這樣哪能掌握平方根的性質呢？所以當老師再追問時，又出現了類似錯誤。只有真正理解了才會求的平方根。平時的教學中，針對學困生或基礎薄弱的學生，我們不妨換位思考一下。課堂提問時，簡單問題留給基礎薄弱的學生，從先后順序上，先提問學困生；布置作業與完成情況方面，采取分層的方式，對基礎薄弱的學生不做統一要求，只完成基本的部分或選做；而對優秀生則適當增加特征類題目，真正做到因材施教。

三、深度學習應該拾級而上

教學的過程中，當學生掌握了基本知識之后，要引導學生在已有的基礎上進一步深化認識和理解，這樣的過程其實就是深度學習。好的課堂教學應該是有深度的，但不一定是難度大的；反過來，難度大的課堂不一定有深度。教學中，如何能讓深度學習在學生層面上落地生根，關鍵取決于教師對設計的問題是否適合于學生學習。在圓周角復習中，為了讓學生進一步理解圓周角與銳角三角函數的關系，我設計了這樣一個問題：

如圖2，⊙O的半徑為5，AB是直徑，BC的長是6，則cosA的值為________________。

當學生能夠順利解決時，可設法讓學生的思維拾級而上，于是我對問題進行了變形。

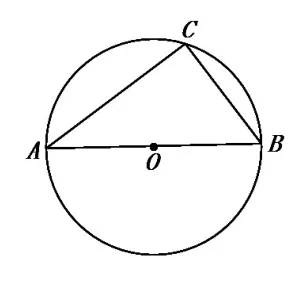
圖2

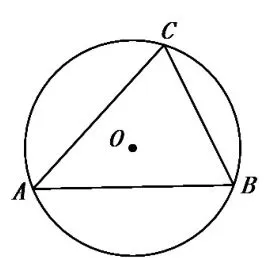
圖3

圖4

學生思考時，可能會想著連接OA或OB或OC；當發現無法解決時，則有學生想到添加如圖4所示的輔助線，利用同弧上的圓周角相等、直徑所對的圓周角是直角、銳角三角函數等方法將問題解決。學生學習數學就是思維的訓練。教學中，拾級而上的教學設計才是適合學生學習的，才可能促進學生的思維逐步提升，學生的學習也才會是有深度的。

四、有效教學促進學生發展

設計適合的有深度的數學教學就是追求有效教學。有效教學立足于學生的認知基礎和已有的學習經驗，站在學生的角度尋找解決問題的策略與途徑，改進學習方式與方法，設計教學時總是朝著“激發學生的學習潛能，鼓勵學生大膽創新與實踐”的方向進行謀劃。

對于基礎薄弱的學生采取小步走、多層次、勤練習、常反饋的由易到難、由淺入深的迂回措施，該分解的分解，該鋪墊的鋪墊。解題教學時可能會將一個題目分解成兩個或多個小題目，讓學生容易上手，不至于失去學習的信心。也可能是采取有針對性的輔導，使基礎薄弱的學生感覺到教師的關心、愛護和幫助。對于學習優秀的學生，更要因材施教，關注優秀學生的思維層次和解決綜合問題的能力。通過適宜的方法，一方面讓優秀學生更加優秀，另一方面讓先知先覺者帶動后知后覺者，促進學生的整體進步。

隨著課堂教學改革的不斷深入，教學的過程越來越重視學生的學，重視學生的學習過程及思考問題的方式方法。傳統的課堂教學注重的是教師的教，教師主宰著課堂，教師是課堂的表演者，學生在課堂上只是聽眾和觀眾，在看教師的表演。隨著教育教學改革的推進，大家逐漸意識到：在課堂教學中，學生才是真正的學習的主人，只有學生進入了學習的狀態，教學才是有效的。在數學學習的過程中，只有細心觀察、認真思考、不斷反思與提煉，才能發現數學的規律及本質，才能不斷提高自己的學習能力。隨著學生認知水平的提高，他們才會理解到數學知識中蘊涵的豐厚的思想方法，才會不斷生長出解決問題的能力，才可能變成有智慧的人。學習上、生活中，不能一條道走到黑，要注意觀察和思考，要注意解決問題的策略和藝術；要靈活多變，該搭橋鋪路時要搭橋鋪路，該峰回路轉時就峰回路轉。學以致用，無論是數學學習還是生活方式，都需要在學習和生活的過程中不斷反思，不斷提煉，這樣學習的方法會更好，對數學知識的理解會更全面。

（作者為江蘇省特級教師，江南大學附屬實驗中學教師）

本文系江蘇省教育科學“十三五”規劃重點自籌課題“初中數學‘深度學習’資源建設的理論與實踐研究”（課題編號：B-b/2016/02/155）的階段性研究成果。