糾“錯”有“措”
——一元一次方程的常見錯誤剖析及解決策略

陳 俊

糾“錯”有“措”
——一元一次方程的常見錯誤剖析及解決策略

陳 俊

一元一次方程是學習其他數學知識的重要基礎，我們要重視其概念的理解，運用恰當的方法解方程.現舉例剖析，望同學們引以為戒.

一、認識“錯”

1.概念不清.

我們要掌握識別一元一次方程的四個要領，即：只含有一個未知數、未知項的次數均為一次、是整式方程、化簡后一次項的系數不為0.

例1 下列各式中，是一元一次方程的有_______（.填序號）

（1）m=0；（2）-3+0.4y=8；

【錯解】（2）、（4）.

【剖析】（1）與（2）均滿足一元一次方程的定義；（3）有兩個未知數，不滿足“一元”；（4）不是整式方程；（5）未知項最高次數為二次，不滿足“一次”.

【正解】（1）（2）.

例2 若（a+1）x+3=5是關于x的一元一次方程，則a________.

【錯解】a=-1.

【剖析】此題考查了識別要領中的“化簡后一次項的系數不為0”，故要滿足a+1≠0.

【正解】a≠-1.

例3 若x|a|+3=5是關于x的一元一次方程，則a=_______.

【錯解】1.

【剖析】此題考查了識別要領中的“未知項的次數均為一次”，故要滿足 | a|=1.

【正解】±1.

變式1 若（a+1）x||a+3=5是關于x的一元一次方程，則a=_______.

【錯解】±1.

【剖析】此題考查了識別要領中的“未知項的次數均為一次”與“化簡后一次項的系數不為0”，故要同時滿足 ||a=1且a+1≠0.

【正解】1.

2.解法不當.

（1）一味“連等于”.

例4 解方程：5x-3=2x.

【錯解】5x-3=2x=5x-2x=3=x=1.

【剖析】對方程進行變形時方程的解雖然不變，但新的方程的兩邊與原方程兩邊的值都不同了，解方程不能用“連等于”.

【正解】5x-2x=3.

（2）移項不變號.

例5 解方程：3x+1=4x+1.

【錯解】移項，得3x+4x=1+1.

【剖析】解方程時，移項要改變符號.本題錯在將“3x”和“1”這兩項從方程一邊移到另一邊時沒有改變符號.

【正解】移項，得3x-4x=1-1.

（3）錯誤去括號.

①乘法分配不到位.

【錯解】去括號，得x+1=6.

【剖析】去括號時沒有把括號外的數分配到括號中的每一項.

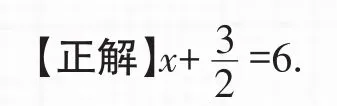
②改變符號不仔細.

例7 解方程：2（x-1）-（x+3）=-3（x+1）.

【錯解】去括號，得2x-2-x+3=-3x+3.

【剖析】去括號時，遇到括號前面是“-”號的，要改變括號里的每一項符號.

【正解】去括號，得2x-2-x-3=-3x-3.

（4）盲目去分母.

①漏乘個別項.

【錯解】去分母，得x+5-1=3x+2.

【剖析】去分母時，方程兩邊各項都應乘以最簡公分母，不能漏乘（常數項常被漏乘）.

【正解】去分母，得x+5-3=3x+2.

②分子少括號.

【錯解】去分母，得2x-1-x+2=12-x.

【剖析】分數線除了代替“÷”外，還具有括號的作用，如果分子是一個多項式，應該把它看作一個整體，用括號括起來.

【正解】去分母，得2（x-1）-（x+2）=3（4-x）.

（5）匆匆寫結果.

①錯位相除.

例10 解方程：2x=3.

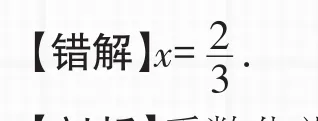
【剖析】系數化為1時方程兩邊都除以未知數的系數而不是常數，應把未知數的系數作分母.

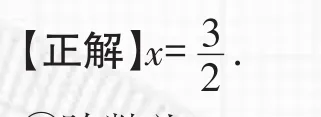
②除數為0.

例11 解關于x的方程：mx-2n=-2nx+m.【錯解】原方程化為（m+2n）x=m+2n.

x=1.

【剖析】方程的兩邊都除以同一個數時，必須確保這個數不為0，所以要對m+2n是否為0進行討論.

【正解】原方程化為（m+2n）x=m+2n.

當m+2n≠0時，x=1；

當m+2n=0時，原方程的解為任意實數.

（6）錯誤用性質.

【剖析】把分母中的小數化成整數是利用分數的基本性質，不是運用等式的性質，上述錯解混淆了這兩個基本性質.

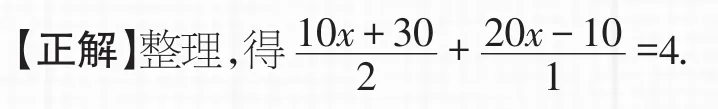
感悟：以上錯誤究其原因，主要是對一元一次方程的概念內涵和解方程時所用到的數學性質掌握不牢所致.因此，在學習一元一次方程時，一定要正確認識相關概念，正確理解相關性質，從而提高自己的解題能力.

二、感悟“錯”

1.樹立“正確解題”的意識.

有的同學總是認為自己會做，只不過粗心而已，或者認為錯這么一點沒多大關系，但實質卻反映出學習過程的不嚴謹，對數學概念和性質認識模糊，容易混淆，從而日漸退步.

2.養成“嚴謹思維”的習慣.

如從一元一次方程的概念中要能悟出四個識別要領，從表面看，方程要滿足“一元”和“一次”，但透過表面看本質，為了能讓方程滿足“一元”和“一次”，就必須滿足“整式方程”和“一次項的系數不為0”的條件.解方程時，每做一步都要思考運用到的性質依據，如等式的基本性質、分數的基本性質等，做到“步步有據”.

3.掌握“剖析錯誤”的方法.

同學們應堅持用好錯題集，將解題過程中出現的錯誤及時進行自我小結、自我點評，不斷反思，避免類似的錯誤再出現.還可以在數學探究小組內互相出一道自己做錯過的同類題型，開展小組“互查互糾”活動，從而讓自己對錯誤的類型、原因有更深刻的認識，并反思出糾正錯誤的方法.

（作者單位：南京師范大學第二附屬初級中學）