電動空氣舵執行機構建模與參數辨識

劉 博，祝學軍，南宮自軍，牛智玲

(中國運載火箭技術研究院，北京 100076)

電動空氣舵執行機構建模與參數辨識

劉 博，祝學軍，南宮自軍，牛智玲

(中國運載火箭技術研究院，北京 100076)

針對使用機電作動器(EMA)的飛行器空氣舵執行機構模型確認需求，考慮舵軸彈性及機構中的干摩擦，通過綜合兩自由度(DOF)開環動力學方程和EMA伺服系統PID控制器，建立了執行機構五階傳遞函數(TF)模型。根據TF特征，提出了模型參數約束條件下，采用頻率響應函數(FRF)測量數據辨識TF模型參數的改進正交多項式擬合法，完成了參數辨識。辨識結果表明：兩自由度動力學模型比一般廣泛采用的單自由度模型更準確地反映了空氣舵執行機構動力學特征；本文提出的改進正交多項式擬合法可以實現位置跟蹤系統TF參數辨識，辨識模型FRF曲線與實測數據吻合良好。

空氣舵;機電作動器(EMA)；系統建模；參數辨識

0 引 言

執行機構是飛行器控制系統的關鍵組成部分，用于產生控制力，改變飛行器飛行軌跡和姿態，其動力學傳遞函數(Transfer function，TF)在控制系統設計中必須予以充分考慮，否則可能導致姿態控制系統穩定裕度不足，甚至失穩[1-3]。當飛行器在大氣層內高速飛行時，采用空氣舵執行機構是比較常見的，一般包括伺服系統和空氣舵機構兩個單元。

伺服系統方面，在飛行器減重、減維護和實戰化需求牽引下，機電作動器(Electromechanical actuator，EMA)憑借其重量輕、高效率、高可靠、易維護、易安裝等優點近年來在航空航天飛行器中得到了廣泛使用[4]。然而，EMA的性能受負載、系統間隙和飽和非線性等因素影響比較明顯。為解決這些問題，國內外學者開展了大量的研究，在分析摩擦、間隙、飽和等因素對EMA穩態和動態特性影響的基礎上，通過內環控制策略[5]、先進控制方法等改善EMA性能[6-9]，也有學者從整個飛行控制系統角度通過優化的集成伺服控制方法彌補EMA飽和的問題[10-11]。同時，隨著EMA的日益廣泛使用，為適應其負載特點，電動伺服加載系統研究也受到了關注[12]。

在工程實際中，伺服系統和空氣舵機構一般由不同的單位按照控制系統提出的指標設計生產。由于二者之間存在動力學耦合，因此對最終裝配完畢的空氣舵執行機構的傳遞特性還需要進行聯合測試確認，獲取傳遞特性參數，進而為控制系統設計分析和仿真提供更準確的模型數據。因此，本文對采用EMA的飛行器空氣舵執行機構開展了建模研究，在此基礎上提出了基于頻率響應函數(Frequency response function，FRF)測試數據的TF參數辨識方法，實現了執行機構模型確認。

1 系統建模

1.1系統組成及分析

一般電動空氣舵執行機構如圖1所示，包括EMA伺服系統和空氣舵機構兩部分，其中EMA伺服系統由驅動控制器和作動器組成。空氣舵通過舵軸與搖臂連接，舵軸通過軸承安裝于支撐艙段上。執行機構收到飛行控制器發出的舵面偏轉位移指令后，驅動控制器驅使作動器推動搖臂使舵軸帶動舵面偏轉，從而產生氣動控制力，通過舵軸和軸承傳遞到飛行器，完成飛行器姿態和軌跡控制的目的。

采用空氣舵進行飛行控制時，執行機構的頻率響應特性是一個重要因素。執行機構頻帶越寬，就能獲得更快的控制力響應[5]。在較寬的頻帶內討論空氣舵執行機構頻響特性時，舵軸的彈性就不可忽略了，舵軸和舵面應被看作是在作動器輸出激勵下的彈簧質量系統。此時，整個執行結構不能按照常規考慮飛行器執行機構的單自由度系統來建模[6,8]，否則會導致較大的誤差。

伺服系統本身十分復雜，但是為了抓住主要因素簡化系統建模，作動器內部的減速機構和滾珠絲杠等零件的轉動慣量統一折合到伺服電機轉子上，用Jm表示，同時為了便于圖示，將角運動慣性元件、彈性元件和阻尼元件采用對應的線運動形式元件進行描述，可得到圖2中的兩自由度空氣舵執行機構數學模型示意圖。圖中，Cm為作動器等效阻尼系數，Te為電機輸出力矩，Jr為空氣舵繞舵軸的轉動慣量，K為舵軸扭轉剛度，C為粘性阻尼系數，Tf為舵軸轉動過程的干摩擦力矩，θm、θf和θr分別為電機輸出轉角、舵軸輸入轉角和實際舵面轉角，L為θm和θf間的傳動比關系，Tc為氣動控制力對舵軸的力矩。

1.2開環狀態動力學方程

為滿足伺服系統響應的快速性，在EMA電機選型時一般要求其電氣時間常數遠小于機械時間常數，同時電流環調節器時間常數也很小。因此，在總體集成建立傳遞特性模型時可以忽略伺服電機電流環控制的動態，將開環狀態作動器看作一個單自由度系統[5-8]，其動力學方程如下

(1)

(2)

θf=Lθm

(3)

式中：Tload為舵對作動器的反作用力矩，η為作動器機械傳動效率，其余參數均已在前文中說明。

空氣舵的運動方程為

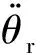
(4)

其中，摩擦力矩Tf表達式為

(5)

在地面測試時氣動力矩Tc=0。同時，地面測試一般采用簡諧或掃頻激勵，因此可以對非線性干摩擦阻尼力矩做等價線性化處理，得到等效粘性阻尼系數Cr[13]

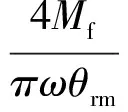
(6)

式中：ω和θrm分別為舵擺動圓頻率和幅值。此時，式(4)可改寫為

(7)

1.3系統綜合

在式(1)基礎上，伺服系統采用位移反饋和PID控制器實現對飛行控制器舵偏指令的閉環跟蹤

(8)

e=θc-θf

(9)

式中：Kp、Ki和Kd為PID控制器的系數，按照控制系統指標要求，采用Loop Shaping技術確定[14]；θc為飛行控制器發出的舵面偏轉指令。

對式(1)、式(7)和式(8)進行Laplace變換，得到整個執行機構系統框圖見圖3，其中，s為Laplace域的復變量。

實際飛行中，氣動控制力由舵面產生，從飛行控制需求角度，希望θr=θc。然而，由圖1和圖3可見，由于伺服系統位移反饋傳感器在作動器輸出端，并不在舵面上，那么即使伺服系統可以實現理想的位置跟蹤，也只能保證θf=θc，因此需要通過伺服系統和空氣舵機構聯試獲取從θc到θr的傳遞特性。

綜合式(1)～(9)，可得空氣舵執行機構的TF，令其為g(s)，則

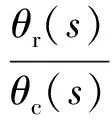
(10)

式中：

a3=CKdLη，a2=(CKp+KKd)Lηa1=(CKi+KKp)Lη，a0=KKiLηb5=JmJrη，b4=(JrKdL+JmC+JrCm+JmCr)η+CJrL2

b3= (CKd+CrKd+JrKp)Lη+(CCm+CrCm+

JmK)η+(JrK+CCr)L2

b2=(CKp+CrKp+JrKi+KKd)Lη+CmKη+CrKL2b1=(CKi+CrKi+KKp)Lη，b0=KKiLη

可見，b0=a0，這表示在靜態和低頻輸入指令時，舵面轉角與指令是1∶1傳遞，體現了位置跟蹤系統的特征。

2 參數辨識方法

2.1辨識問題描述

對于式(10)中TF的確定，并不需要辨識物理參數，只要通過測試數據得到ak,k=0,…,3和bk,k=0,…,5即可開展飛行控制系統設計與仿真。實際測試中，一般并不直接進行TF的測試，而是通過FRF測試完成TF參數的辨識。

通過FRF數據辨識TF參數的方法中效果比較理想的是有理分式正交多項式法[15]。然而，該方法不能處理b0=a0約束，因此，需要對其進行改進，完成零次項系數約束條件下的TF參數辨識，即在

b0=a0

(11)

約束下采用式(10)對應的FRF

(12)

在n個頻率點上的測試數據g(iωj),j=1,…,n擬合辨識ak,k=0,…,3和bk,k=0,…,5。

2.2改進的正交多項式法

作為方法，并不局限于式(12)中的參數辨識，而是面向一般線性系統提出，其FRF均可表示為類似式(12)的有理分式形式

(13)

式中：ak，k=0,…,m和bk，k=0,…,l為待辨識參數。

首先，將式(13)的FRF在測試頻點上表示為正交多項式形式

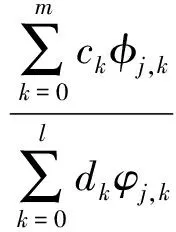
(14)

式中：函數φ和φ均為Forsythe多項式(半函數)的正交基[15]，滿足

(15)

(16)

上標*表示共軛。同時，

a=Gac

(17)

b=Gbd

(18)

此時，約束條件式(11)變為

Ga1c-Gb1d=0

(19)

式中：Ga1、Gb1分別為Ga和Gb的第一行元素構成的向量。

然后，定義誤差向量

E=Pc-Td-W

(20)

式中：

參數辨識是個曲線擬合優化問題。因此，構造最小二乘擬合目標函數，同時采用Lagrange乘子法消除約束條件(19)得如下優化問題

minV=EHE+λ(Ga1c-Gb1d)

(21)

式中：λ為Lagrange乘子，上標H表示共軛轉置。經推導，式(21)的解滿足如下方程

(22)

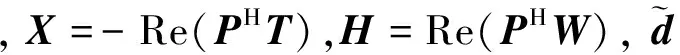
求解式(22)得到正交多項式系數向量c和d，代入式(17)和式(18)即可得到TF有理分式多項式的系數a和b。

3 參數辨識結果及討論

圖4為某空氣舵執行機構FRF實測數據及采用上述模型和參數辨識方法對其進行曲線擬合的結果。閉環EMA伺服系統和空氣舵機構兩個單元諧振頻率接近，因此幅頻傳遞曲線兩個諧振峰耦合形成諧振帶，五階系統辨識結果與實測數據吻合良好。

1) 由圖4可見，由于在曲線擬合方法中引入了式(11)約束，低頻部分幅頻傳遞趨向1∶1，相位差趨向于0 rad，符合位置跟蹤系統傳遞特性的特征。

對于中頻動態傳遞特性要求較高的隨動系統或者一般隔振系統[13]的傳遞函數，不僅b0=a0，而且b1=a1。此時需將式(19)中Ga1和Gb1分別更改為Ga和Gb的前兩行元素構成的矩陣即可采用本文方法完成參數辨識。

2) 如果按照通常處理飛行器執行機構的方法，忽略舵軸彈性，將舵慣量和舵面負載折合到作動器電機轉子上[8]，即兩自由度開環動力學模型退化為單自由度模型，則式(10)執行機構TF退化為一個三階系統，m=2，l=3。由圖4可見，采用此模型時，系統辨識誤差較大。

無論是三階還是五階TF模型，在低頻部分幅頻傳遞特性辨識結果均略小于實測結果，這主要是由于實際執行機構中含有的傳動間隙引起的，工程中可通過試驗測量間隙量，在設計控制系統時予以考慮。盡管如此，五階TF模型對實測數據的吻合程度整體上明顯優于三階TF模型，從而驗證了兩自由度動力學模型的合理性。

4 結 論

針對使用EMA的飛行器空氣舵執行機構模型確認需求，考慮舵軸彈性及舵機構中的干摩擦，得到了系統的兩自由度運動方程，并通過綜合伺服系統PID控制器，建立了空氣舵執行機構的五階TF模型。在此基礎上提出了模型參數約束條件下，改進的有理分式正交多項式參數辨識方法，完成了模型參數辨識，得到以下結論：

1)在較寬頻帶內討論空氣舵執行機構傳遞特性時，考慮舵軸彈性，采用兩自由度模型可以比單自由度模型更準確地反映系統動力學特征。

2)本文提出的改進的有理分式正交多項式擬合法可以實現位置跟蹤系統TF參數辨識，辨識模型FRF曲線與實測數據吻合良好。

[1] Noll R B，Zvara J. Structural interaction with control systems [R]. NASA-SP-8079，1971.

[2] Dhekane M V，Lalithambika V R，Dasgupta S, et al. Modeling of control/structure interaction in launch vehicle-a flight experience[R]. AIAA-1999-4132，1999.

[3] Kakade A, Kurode S, Sor R. Sliding mode control for the fin actuation mechanism[C]. IEEE International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), Pune, India, 2016: 273-277.

[4] Li J M, Yu Z Y, Huang Y P, et al. A Review of electromechanical actuation system for more electric aircraft[C]. IEEE/CSAA International Conference on Aircraft Utility Systems (AUS), Beijing, China, October 10-12, 2016.

[5] Habibi S, Roach J, Luecke G. Inner-loop control for electromechanical (EMA) flight surface actuation systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(5): 1-13.

[6] Lyshevski S E, Skormin V A, Colgren R D. High-torque density integrated electro-mechanical flight actuators[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 174-182.

[7] Han S I, Lee J M. Adaptive dynamic surface control with sliding mode control and RWNN for robust positioning of a linear motion stage [J]. Mechatronics, 2012, 22(2): 222-238.

[8] Lu H, Li Y, Zhu C. Robust synthesized control of electromechanical actuator for thrust vector system in spacecraft [J]. Computers amp; Mathematics with Applications, 2012, 64(5): 699-708.

[9] Wang N, Lin W, Yu J. Sliding-mode-based robust controller design for one channel in thrust vector system with electromechanical actuators[J]. Journal of the Franklin Institute, 2017(In Press).

[10] Kim S H, Lee Y I, Tahk M J. New structure for an aerodynamic fin control system for tail fin-controlled stt missiles[J]. Journal of Aerospace Engineering, 2010, 24(4): 505-510.

[11] Kim S H, Tank M J, Lee H J. Experimental study on integrated servo control for canard-controlled missiles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1467-1474.

[12] 陳康, 黃勇, 孫力. 電動直線舵機方波加載系統研究[J]. 宇航學報, 2008, 29(5): 1515-1519. [Chen Kang , Huang Yong , Sun Li. The research of linear rudder square-direction electric loading system [J]. Journal of Astronautics, 2008, 29(5): 1515-1519.]

[13] 胡海巖, 孫久厚, 陳懷海. 機械振動與沖擊版社[M]. 北京: 航空工業出版社, 2002.

[14] Schinstock D E, Scott D A, Haskew T A. Transient force reduction in electromechanical actuators for thrust-vector control [J]. Journal of Propulsion and Power, 2001, 17(1): 65-72.

[15] Richardson M H, Formenti D L. Parameter estimation from frequency response measurements using rational fraction polynomials[C]. Proceedings of the International Modal Analysis Conference. 1982: 167-182.

ModelingandParameterIdentificationofanAircraftRudderSystemwithanElectromechanicalActuator

LIU Bo, ZHU Xue-jun, NANGONG Zi-jun, NIU Zhi-ling

(China Academy of Launch Vehicle Technology, Beijing 100076, China)

In this paper, modeling and parameter identification of an aircraft rudder system with an electromechanical actuator (EMA) is discussed to validate its mathematical model through frequency response function (FRF) test. Firstly, a five order transfer function (TF) model of the rudder system is established by synthesizing its two-degree-of-freedom (DOF) dynamic equations and a servo PID controller, in which the rudder axis is modeled as a damped spring and the Coulomb friction is also included. Then, in view of the characteristics of the TF model, an improved parameter identification method based on the rational fraction orthogonal polynomials with a parameter constraint is presented. Finally, the TF parameters are identified by applying the presented method to the FRF test data. It is indicated by the identification results that, 1) the two-DOF model figures the rudder system better than the generally used one-DOF one, and 2) excellent agreement is achieved between the identified mathematical model and the FRF measurement data, which demonstrates the efficacy of the proposed TF parameter identification method for the position tracking systems.

Air rudder; Electromechanical actuator (EMA); System modeling; Parameter identification

V442；O32

A

1000-1328(2017)11- 1147- 06

10.3873/j.issn.1000- 1328.2017.11.002

2017- 07- 03;

2017- 09- 18

劉博(1982-)，男，博士，高級工程師，主要從事航天運載飛行器結構動力學、載荷與環境研究與設計。

通信地址：北京市9200信箱1分箱-1#(100076)

電話：(010)88524819

E-mail:liubo_1014@163.com