固體導彈助推段自抗擾制導控制一體化設計方法

聶文明，李惠峰

(北京航空航天大學宇航學院, 北京 100191)

固體導彈助推段自抗擾制導控制一體化設計方法

聶文明，李惠峰

(北京航空航天大學宇航學院, 北京 100191)

針對存在建模誤差及外部干擾情況下的固體導彈助推段制導控制一體化(IGC)設計問題，給出一類自抗擾制導控制一體化設計方法。首先考慮質心運動與繞質心運動間的耦合，結合軌跡線性化方法建立了面向控制的固體導彈助推段制導控制一體化設計模型。采用擴張狀態觀測器(ESO)實時估計系統建模誤差與外部干擾，進而基于反步法結合反饋線性化方法,提出一類考慮質心運動與繞質心運動間的耦合作用的自抗擾制導控制一體化設計方法，并通過Lyapunov穩定性理論證明了該制導控制一體化設計方法可保證閉環系統的穩定性，解決了傳統制導控制系統分離設計方法無法保證閉環系統穩定性的問題。最后，數值仿真校驗了本文所提的助推段自抗擾制導控制一體化(ADRIGC)設計方法的控制性能及抗干擾性能。

助推段制導控制一體化模型；制導控制一體化；擴張狀態觀測器；反步控制；固體導彈

0 引 言

制導控制一體化(Integrated guidance and control, IGC)設計是一種從整體上設計導彈制導控制系統的思想。不同于傳統的設計方法，IGC充分考慮制導系統與控制系統的耦合關系，把二者作為一個整體考慮，根據導彈質心運動信息直接產生執行機構控制指令[1]，既能減少設計周期和成本，還能弱化對導彈機動性的約束，避免導彈的失穩現象，改善導彈控制中的過程控制特性及終端精度[2-3]。

傳統的導彈制導與姿態控制系統分離設計思想可概括為：基于時域分離假設，將制導控制系統分為制導回路與姿控回路，忽略質心運動與繞質心運動間的耦合，分別設計制導律與姿態控制律，最后將設計好的子系統整合后，若整體性能未達到期望的要求，則需重新設計每個子系統，反復迭代，直到滿意為止[4]。為了改善跟蹤性能，各類非線性現代控制理論被用于制導律與姿態控制律的設計，如魯棒控制[5]、滑模控制[6]、增益調度控制[7]、反步控制[8]及有限時間控制[9]等，但由于分離設計思想本身的局限性，得出的控制系統只能改善各子系統自身控制性能，而無法保證整合后的制導控制系統總體的穩定性與控制性能。

IGC設計則把制導系統和控制系統視為整體，設計過程中不依賴于時域分離假設，即使在存在不確定性或導彈機動的情況下，也不會出現失穩現象，從而保證制導精度[10]。自Williams等[1]于20世紀80年代提出制導與控制一體化設計以來，許多學者依據這種整體設計的思想開展了研究工作，尤其是近30年來，制導與控制一體化設計取得了較豐富的研究成果。最早的制導控制一體化設計采用了線性最優控制方法[1，11]，但是由于導彈的制導控制系統自身的強非線性與強耦合，線性控制方法不能滿足設計要求。因此，基于非線性最優控制理論的IGC設計方法被提出，為解決Hamilton-Jacobi-Bellman (HJB)方程難以求解的問題，各國學者在求解制導控制一體化最優控制問題時，分別采用了兩種數值解法：狀態依賴Riccati方程法[12]和θ-D方法[13]。上述設計方法均基于復雜的導彈六自由度非線性動力學方程，存在難以在線實時求解的問題，并且設計中未考慮未建模動態或外部擾動對控制系統性能的影響。此后，上述問題被很大程度地簡化，出現了近似一體化的思路[9，14-15]，該思路將姿態角動態近似為某類參考模型，并在設計制導律時將該近似模型動態考慮在內，但其實際上仍是一種分離設計的思路，與傳統設計思路沒有本質區別。為解決上述問題，各國學者分別從制導控制一體化模型設計與一體化控制方法設計兩個角度對制導控制一體化設計問題展開了廣泛研究[16]。目前主要有兩類一體化模型：相對位置模型和視線角模型[16]，基于這兩類模型，各國學者分別采用反步控制[17-18]、自抗擾控制[19]、滑模控制[20]、自適應控制[21]和魯棒控制[22]等方法給出了制導控制一體化控制設計方法。

現有IGC設計方法的研究均針對導彈打擊段展開，為解決導彈助推段的制導控制一體化設計問題，則需要結合導彈上升段飛行力學特性及控制需求，同時考慮模型復雜度、方法復雜度、系統穩定性、抗干擾特性等問題，給出可行的一體化設計方法。本文以單噴管兩級固體導彈為研究對象，針對其助推段IGC設計問題展開研究，主要創新點如下：1)結合助推段飛行力學特性和控制需求，引入側滑角以主動控制固體導彈助推段速度，并考慮質心運動與繞質心運動間的耦合作用，建立了助推段制導控制一體化設計模型，進而采用軌跡線性化方法，將原非仿射模型轉化為仿射模型，最終給出了面向控制的固體導彈助推段IGC設計模型；2)采用反步法設計一體化設計框架，結合反饋線性化方法設計得到了助推段IGC控制器，解決了傳統設計方法無法保證制導控制綜合系統穩定性的問題，并從理論分析的角度證明了本文提出的自抗擾IGC(Active disturbance rejection IGC, ADRIGC)設計框架可實現閉環系統的穩定；3)基于擴張狀態觀測器(Extended state observer, ESO)設計了具有自抗擾特性的助推段制導控制一體化控制系統[19]，提高了閉環控制系統的抗干擾性能，改善了存在建模誤差及外界干擾情況下的過程跟蹤性能及終端精度。

1 面向控制的助推段IGC設計模型

本節首先給出固體導彈助推段質心運動模型與繞質心運動模型，然后針對模型存在的非仿射問題，采用軌跡線性化方法將模型轉化為仿射系統，得到面向控制的助推段IGC設計模型。

1.1助推段IGC運動模型

單噴管固體導彈的中心噴管僅能提供俯仰力矩與偏航力矩，而在實際設計中，通常采取滾轉穩定控制策略，通過安裝滾轉反作用控制系統(Reaction control system,RCS)等方式保證滾轉通道姿態穩定。因此本文針對其俯仰通道與偏航通道的IGC設計問題展開研究。基于上述分析，建立如下標稱模型：

(1)

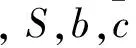
需要指出的是，對于固體導彈而言，無法通過改變推力大小的方式實現對速度的控制,因此區別于文獻[21]等文獻中的助推段質心運動模型，本文給出的助推段IGC運動模型將側滑角引入質心運動方程，以實現對速度的主動控制。另一方面，攻角、側滑角在運動方程中以非仿射的形式出現，增加控制自由度的同時也增加了控制系統設計的難度。

1.2面向控制的助推段IGC設計模型

為利用并補償質心運動與繞質心運動之間的耦合作用，本節首先建立考慮上述耦合的助推段IGC設計模型；進而為解決IGC設計模型存在的非仿射問題，結合導彈助推段存在標稱軌跡的特點，采用軌跡線性化方法將原非仿射IGC設計模型轉化為仿射IGC設計模型，得到了面向控制的IGC設計模型。

記vθ=vsinθ，為方便表述并考慮飛行環境干擾，將式(1)重寫為如下緊湊形式：

(2)

(3)

(4)

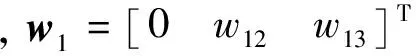
(5)

聯立式(2)、式(4)，可得如下面向控制的助推段IGC設計模型：

(6)

2 控制器設計

本節將基于式(6)所示的面向控制的IGC設計模型，首先假設建模誤差及外界干擾已知，給出助推段IGC設計方法，然后通過設計ESO，實時估計未知的建模誤差與外界干擾并反饋至控制器，得到助推段ADRIGC設計方法，最后通過Lyapunov穩定性理論，證明上述ADRIGC控制器可保證閉環系統的穩定性。

2.1助推段IGC設計方法

引入輔助控制量x1d,x2d,x3d，其中x1d=x1nom為助推段標稱軌跡，x2d,x3d為IGC設計中待設計的量，稍后將給出定義。

定義如下誤差向量：

(7)

聯立式(6)、式(7)可得如下誤差動態方程：

(8)

基于反步法，分別利用PD控制與反饋線性化控制可得如下IGC控制器：

(9)

x2d,x3d分別滿足如下方程：

(10)

式中：K1∈R2×3,K2∈R2×2,K3∈R2×2,為待設計控制器參數矩陣。

注1. 式(10)所示x2d表示IGC設計中實際的期望姿態角指令，而在傳統的分離設計中，期望姿態角指令為x2nom，兩者之間的不同在于Δx2d，而Δx2d是對質心運動與繞質心運動之間的耦合起補償作用的項，由此設計得到的姿態角指令x2d可實現對質心運動跟蹤誤差的主動控制，而傳統分離設計思路下的姿態控制器未考慮上述耦合，姿態控制器的改進也僅能實現對x2nom的跟蹤，而無法影響質心運動的跟蹤誤差。

2.2自抗擾IGC設計方法

式(9)所示的IGC控制器中含有未知建模誤差w1和外干擾項di,i=1,2,3。為使控制系統具有實時補償上述不確定項的能力，需要實現對上述未知項的實時估計。本節采用ESO實現對各不確定項的實時觀測[23]，以保證式(9)所示IGC控制器在工程應用中的可實現性。

(11)

(12)

則可設計如下ESO：

(13)

基于ESO觀測結果，式(9)中總擾動w1+d1,d2及d3可由其觀測值代替，從而可得如下ADRIGC控制器:

(14)

基于ESO觀測值，x2d,x3d可寫為如下形式：

(15)

2.3穩定性證明

引理1[24]. 在式(12)所示ESO中，設計如下形式的觀測器參數：

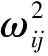
(16)

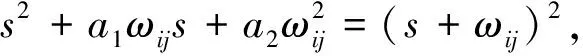
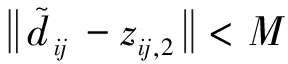
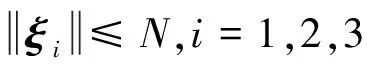
定理1. 對于控制器參數矩陣K1∈R2×3，K2∈R2×2,K3∈R2×2。取c1為K1,K2,K3中各元素最小值，若滿足K1gt;0,K2gt;0,K3gt;0且c1gt;3M/N，則式(14)所示的ADRIGC控制器可實現系統的閉環穩定。

證. 定義Lyapunov函數：

(17)

對式(17)求導可得：

(18)

將式(8)、式(14)、式(15)代入式(18),可得：

(19)

基于假設1與假設2可得：

(20)

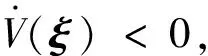
3 仿真校驗

本節將給出仿真結果及分析，首先在無外部干擾的情況下，對比分析了基于傳統設計思路[25]與IGC設計思路的兩類軌跡跟蹤控制器性能，校驗本文提出的IGC設計方法的有效性；然后針對不同氣動干擾情況進行IGC控制系統仿真，校驗了基于ESO的ADRIGC控制器的抗干擾特性。

本節仿真以二級固體導彈為研究對象，導彈起飛后68 s進行一、二級分離，拋棄第一級干重，終端高度76 km，終端速度3758 m/s，第一級控制力矩約束為：|Mcb1|lt;866590 N·m，第二級控制力矩約束|Mcb2|lt;3341210 N·m。以下仿真算例中，仿真步長為0.01s，控制器設計參數與觀測器設計參數均一致，具體如下：

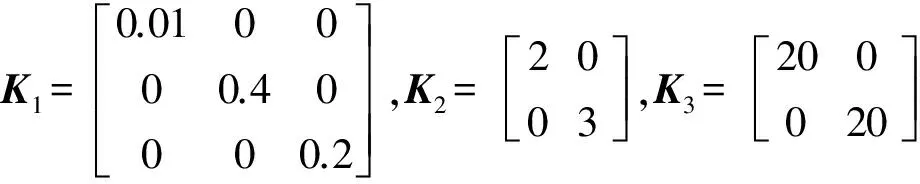
3.1IGC設計有效性仿真校驗

為考察IGC設計思路相對傳統設計思路的優點，分別基于兩種思路設計軌跡跟蹤控制器，并在不考慮大氣擾動的情況下進行數值仿真，兩類控制器均采用標稱控制器，即未引入ESO觀測值(以式(14)、(15)所示的IGC控制器為例，標稱IGC控制器即設置zij=0)。其數值仿真結果如圖1～4所示(注.圖1～4中，u0,uIGC分別代表基于傳統設計和基于IGC設計的控制器)。

從圖1和圖2可以看出，基于IGC設計的控制系統實現了對標稱軌跡的跟蹤，同時保證了導彈姿態的穩定。而基于傳統設計思路的控制系統雖然對攻角和側滑角指令的跟蹤效果優于IGC設計，但是由于傳統設計思路中未考慮制導與姿控系統的耦合，設計的控制器無法在維持姿態穩定的同時保證軌跡跟蹤的精度，因此導致助推段跟蹤誤差越來越大。從圖4可以看出，IGC設計可保證助推段跟蹤誤差絕對值維持在較小范圍內(最大高度跟蹤誤差：160 m，最大速度跟蹤誤差：8 m/s)，而傳統設計高度跟蹤誤差則明顯較大，其中高度跟蹤誤差已超出可接受范圍(最大高度跟蹤誤差：2914 m，最大速度跟蹤誤差：40 m/s)。而圖3所示的控制力矩響應曲線說明整個控制過程中控制量未超出約束值。

圖2給出的姿態響應曲線中，IGC控制下的側滑角在68 s附近出現短暫波動，這是由于此時拋棄一級干重，造成的質量突變引起的。而質量突變直接影響了質心運動，導致軌跡跟蹤出現誤差，由式(14)、(15)可知，上述誤差會產生額外的控制力矩，而基于傳統設計的控制器中未考慮軌跡跟蹤誤差項，因此無法消除質量突變對軌跡跟蹤造成的影響，如圖4所示，傳統設計控制下的高度跟蹤誤差在質量突變后以更快的速度增大，而速度跟蹤誤差也在此處出現波動。

此外，圖4中u0的高度跟蹤誤差曲線從20 s處開始出現快速增長，這是因為在傳統設計思路中，姿態控制器無法消除制導環因建模誤差或外界干擾等導致的跟蹤誤差。而在本仿真算例中，盡管未考慮外界干擾，但軌跡線性化導致式(6)所示的面向控制的模型與式(1)所示的真實模型相比，存在建模誤差，因此會導致制導環的跟蹤誤差。0～20 s內已經出現跟蹤誤差，若不做出補償，將必然導致誤差增加越來越迅速。傳統分離設計的思路的固有缺陷使得u0無法抑制誤差的增長，而基于IGC設計思路,考慮制導環與姿控環的耦合，uIGC可消除該類誤差。

3.2ADRIGC設計抗干擾特性仿真校驗

在試驗2中，為校驗基于本文所提的ADRIGC設計方法的控制系統抗干擾特性，引入大氣干擾，假設氣動力存在如下形式的正弦干擾(以升力為例，阻力與側力干擾同時引入相同形式干擾)：

(21)

表1給出了不同氣動干擾下高度與速度的終端值，ADRIGC即為式(14)所示的控制器，而標稱IGC則未引入對建模誤差及氣動干擾的補償項，由表1不難看出，自抗擾IGC控制的終端精度明顯優于標稱IGC，某些情況下標稱IGC已經發散的情況下，自抗擾IGC的終端控制精度仍保持較好魯棒性，說明自抗擾IGC對較大范圍(較大幅值及頻率范圍)內的氣動干擾均具有很好的抗干擾特性。

表1 不同外部干擾下的終端跟蹤誤差Table 1 Terminal tracking errors with different external disturbances

另外，圖8中的跟蹤誤差明顯小于圖4，這是因為IGC設計方法考慮了制導環與姿控環的耦合，氣動干擾與建模誤差造成的軌跡跟蹤誤差被引入姿態環，最終進入控制器，保證跟蹤誤差始終處于較小范圍。而ESO的引入使外部干擾與建模誤差得以被實時估計并反饋至控制器，因此uADRIGC跟蹤誤差小于uIGC。除跟蹤誤差較小外，uADRIGC的姿態角響應及控制量響應均優于uIGC。進一步證明了本文所提ADRIGC設計方法的有效性。

分別利用常值與矩形波干擾模擬常值風與陣風干擾，其中常值干擾在50 s出現，幅值為氣動力的0.5倍，即0.5F，F表示氣動力，矩形波干擾周期為T=30 s，形式如式(22)所示。從圖 9可以看出，高度與速度跟蹤誤差始終控制在較小范圍內，進一步說明了ADRIGC的有效性與魯棒性。

(22)

4 結 論

本文針對固體導彈助推段IGC設計問題，首先給出了考慮質心運動與繞質心運動間耦合的IGC設計模型，并采用軌跡線性化方法解決了原IGC設計模型存在的非仿射問題，最終得出了面向控制的固體導彈助推段IGC設計模型。基于上述模型提出了一類ADRIGC設計方法，與傳統的分離設計方法相比，ADRIGC設計一方面保證了總體控制系統的理論穩定性，取消了迭代設計過程，簡化了設計工作，弱化了設計中對導彈機動性的約束；另一方面，通過引入ESO實現了對未知項的實時估計與補償，提高了控制精度，改善了響應品質。最終，通過理論分析與數值仿真對上述結論進行了分析與校驗。

[1] Williams D, Richman J, Friedland B. Design of an integrated strapdown guidance and control system for a tactical missile[C].Guidance and Control Conference, Gatlinburg, USA， August 15-17, 1983.

[2] 董飛垚, 雷虎民, 周池軍,等. 導彈魯棒高階滑模制導控制一體化研究[J]. 航空學報, 2013, 34(9):2212-2218.[Dong Fei-yao, Lei Hu-min, Zhou Chi-jun,et al. Research of integrated robust high order sliding mode guidance and control for missiles[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9):2212-2218.]

[3] Shima T, Idan M, Golan O M. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance Control amp; Dynamics, 2012, 29(2):250-260.

[4] 程繼紅. 飛行器控制導引一體化設計方法研究[J]. 海軍航空工程學院學報, 2006, 21(2):227-230.[Cheng Ji-hong. Research on integrated design method for air vehicle’s guidance and control[J]. Journal of Naval Aeronautical Engineering Institute, 2006, 21(2):227-230.]

[5] Yang C D, Chen H Y. NonlinearH∞Robust guidance law for homing missiles[J]. Journal of Guidance Control amp; Dynamics, 1998, 21(6):882-890.

[6] Zhou D, Mu C, Xu W. Adaptive sliding-mode guidance of a homing missile[J]. Journal of Guidance Control amp; Dynamics, 1999, 22(4):589-594.

[7] Buschek H. Full envelope missile autopilot design using gain scheduled robust control[J]. Journal of Guidance Control amp; Dynamics, 1999, 22(1):115-122.

[8] Xu B, Zhang Y. Neural discrete back-stepping control of hypersonic flight vehicle with equivalent prediction model[J]. Neurocomputing, 2015, 154: 337-346.

[9] Chwa D, Jin Y C. Adaptive nonlinear guidance law considering control loop dynamics[J]. IEEE Transactions on Aerospace amp; Electronic Systems, 2003, 39(4):1134-1143.

[10] 梁曉玲. 控制受限的導引與控制一體化設計[D]. 哈爾濱:哈爾濱工業大學, 2015.[Liang Xiao-ling. The integrated design method of guidance and control with control constraints[D]. Harbin:Harbin Institute of Technology, 2015.]

[11] Hughes T, Mcfarland M. Integrated missile guidance law and autopilot design using linear optimal control[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Dever, USA, August 14-17, 2000.

[12] Menon P K, Ohlmeyer E J. Integrated design of agile missile guidance and autopilot systems[J]. Control Engineering Practice, 2001, 9(10):1095-1106.

[13] Xin M, Balakrishnan S N, Ohlmeyer E J. Integrated guidance and control of missiles withθ-Dmethod[J]. IEEE Transactions on Control Systems Technology, 2006, 14(6):981-992.

[14] Chwa D, Jin Y C, Anavatti S G. Observer-based adaptive guidance law considering target uncertainties and control loop dynamics[J]. IEEE Transactions on Control Systems Technology, 2006, 14(1):112-123.

[15] Ju H S, Tsai C C. Longitudinal axis flight control law design by adaptive backstepping[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 43(1):311-329.

[16] 賴超, 王衛紅, 熊少鋒. 攔截大機動目標的三維制導控制一體化設計[J]. 宇航學報, 2017, 38(7):714-722.[Lai Chao, Wang Wei-hong,Xiong Shao-feng. Integrated guidance and control design against highly maneuvering target[J]. Journal of Astronautics, 2017, 38(7):714-722.]

[17] 孫向宇, 晁濤, 王松艷, 等. 考慮通道耦合因素的制導控制一體化設計方法[J]. 宇航學報, 2016, 37(8):936-945.[Sun Xiang-yu, Chao Tao, Wang Song-yan, et al. Integrated guidance and control design method considering channel coupling[J]. Journal of Astronautics, 2016, 37(8):936-945.]

[18] 舒燕軍, 唐碩. 軌控式復合控制導彈制導與控制一體化反步設計[J]. 宇航學報, 2013, 34(1):79-85.[Shu Yan-jun, Tang Shuo. Integrated guidance and control backstepping design for blended control missile based on NDO[J]. Journal of Astronautics, 2013, 34(1):79-85.]

[19] Xue W, Huang C, Huang Y. Design methods for the integrated guidance and control system[J]. Control Theory Appl., 2013, 30(12): 1511-1520.

[20] 王建華, 劉魯華, 王鵬, 等. 高超聲速飛行器俯沖段制導控制一體化設計方法[J]. 航空學報, 2017 (3): 207-219.[Wang Jian-hua, Liu Lu-hua, Wang Peng,et al. Integrated guidance and control for hypersonic vehicles in dive phase[J]. Acta Aeronautica et Astronautica Sinica, 2017 (3): 207-219.]

[21] Erdos D, Shima T, Kharisov E, et al. L1 adaptive control integrated missile autopilot and guidance[C]. AIAA Guidance, Navigation, and Control Conference Minneapolis, Minnesota,USA, August 13-16, 2012.

[22] Yan H, Ji H. Integrated guidance and control for dual-control missiles based on small-gain theorem[J]. Automatica, 2012, 48(10):2686-2692.

[23] 韓京清. 自抗擾控制技術-估計補償不確定因素的控制技術[M]. 北京:電子工業出版社, 2005:184-230.

[24] Zheng Q, Gao L Q, Gao Z. On validation of extended state observer through analysis and experimentation[J]. Journal of Dynamic Systems, Measurement, and Control, 2012, 134(2).

[25] Lu P. Nonlinear trajectory tracking guidance with application to a launch vehicle[J]. Journal of Guidance, Control, and Dynamics, 1996, 19(1): 99-106.

AnActiveDisturbanceRejectionDesignMethodforAscentIntegratedGuidanceandControlofSolidMissiles

NIE Wen-ming, LI Hui-feng

(School of Astronautics, Beihang University, Beijing 100191, China)

This paper presents a novel design method of the integrated guidance and control (IGC) for the solid missiles in the ascent phase subject to modeling uncertainties and external disturbances. Firstly, an ascent model considering the coupling between the guidance and control loops is established. Then it is converted to a control oriented ascent IGC design model based on the trajectory linearization method. The extended state observer (ESO) is adopted to timely estimate the modeling uncertainties and external disturbances to make them available for feedback. Based on the backstepping and feedback control methods, an active disturbance rejection based IGC design method is proposed. The stability analysis of the closed-loop system is provided in the framework of the Lyapunov stability theory. Finally, the numerical simulation demonstrates the efficiency and robustness of the proposed active disturbance rejection integrated guidance and control (ADRIGC).

Ascent integrated guidance and control model; Integrated guidance and control design; Extended state observer; Backstepping control; Solid missile

V412.1

A

1000-1328(2017)11- 1177- 09

10.3873/j.issn.1000- 1328.2017.11.006

2017- 06- 05;

2017- 08- 27

國家重點研發計劃(2016YFB1200100)

聶文明(1990-)，男，博士生，主要從事再入飛行器姿態控制方法，制導控制一體化設計方法研究。

通信地址：北京市海淀區學院路37號(100191)

電話:(010)83229527

E-mail:wenming0912@buaa.edu.cn