執(zhí)行機(jī)構(gòu)故障的航天器姿態(tài)容錯(cuò)控制

耿云海，金榮玉，陳雪芹，李冬柏

(哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所，哈爾濱 150001)

執(zhí)行機(jī)構(gòu)故障的航天器姿態(tài)容錯(cuò)控制

耿云海，金榮玉，陳雪芹，李冬柏

(哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所，哈爾濱 150001)

針對(duì)航天器執(zhí)行機(jī)構(gòu)(飛輪)故障的姿態(tài)控制問(wèn)題，基于線性變參數(shù)(LPV)系統(tǒng)設(shè)計(jì)魯棒變?cè)鲆鍼ID容錯(cuò)控制。考慮轉(zhuǎn)動(dòng)慣量隨時(shí)間變化和執(zhí)行機(jī)構(gòu)乘性故障，將航天器姿態(tài)動(dòng)力學(xué)轉(zhuǎn)化為不確定LPV系統(tǒng)。設(shè)計(jì)控制器時(shí)，利用仿射二次穩(wěn)定的方法降低控制算法的保守性，引入保性能控制保證系統(tǒng)的魯棒性。仿真結(jié)果表明，控制方法是有效的。

航天器姿態(tài)控制；容錯(cuò)控制；執(zhí)行機(jī)構(gòu)故障；線性變參數(shù)(LPV); 魯棒變?cè)鲆婵刂?/p>

0 引 言

在軌航天器由于長(zhǎng)時(shí)間工作在失重、高低溫和強(qiáng)輻射等惡劣環(huán)境中，各種各樣的故障伴隨而生，其中執(zhí)行機(jī)構(gòu)和敏感器發(fā)生故障最為常見(jiàn)[1]。所以，針對(duì)航天器執(zhí)行機(jī)構(gòu)故障，研究姿態(tài)容錯(cuò)控制是至關(guān)重要的。到目前為止，航天器姿態(tài)容錯(cuò)控制方面，已經(jīng)有一定的研究成果。文獻(xiàn)[2]研究了基于PD學(xué)習(xí)型觀測(cè)器的系統(tǒng)故障重構(gòu)方法，能夠快速精確地重構(gòu)航天器執(zhí)行機(jī)構(gòu)故障。文獻(xiàn)[3]在執(zhí)行機(jī)構(gòu)輸出受限的情況下，根據(jù)從狀態(tài)觀測(cè)器得到的故障信息來(lái)重構(gòu)控制器。文獻(xiàn)[4]針對(duì)航天器外部干擾和執(zhí)行機(jī)構(gòu)發(fā)生乘性故障，利用故障觀測(cè)器獲得的故障信息設(shè)計(jì)容錯(cuò)控制器。文獻(xiàn)[5]針對(duì)未知的執(zhí)行機(jī)構(gòu)故障，利用滑模觀測(cè)器和自適應(yīng)故障估計(jì)法獲得故障信息，并據(jù)此設(shè)計(jì)容錯(cuò)控制器，利用Lyapunov方法進(jìn)行穩(wěn)定穩(wěn)定性分析。文獻(xiàn)[6]在允許少量飛輪完全失效的情況下，設(shè)計(jì)了自適應(yīng)反步容錯(cuò)控制器。文獻(xiàn)[7]研究了不依賴于角速度和故障信息的姿態(tài)容錯(cuò)控制。文獻(xiàn)[8]針對(duì)執(zhí)行器和敏感器故障，分別研究了基于H∞的容錯(cuò)控制。

線性變參數(shù)(Linear parameter varying，LPV)系統(tǒng)是一類特殊的線性系統(tǒng)，其狀態(tài)空間矩陣是時(shí)變參數(shù)向量的函數(shù)，時(shí)變參數(shù)體現(xiàn)了系統(tǒng)的非線性和時(shí)變性。LPV控制理論是一種保證系統(tǒng)穩(wěn)定性和動(dòng)態(tài)性能的變?cè)鲆婕夹g(shù)，是時(shí)不變系統(tǒng)控制理論在LPV系統(tǒng)上的推廣[9]。利用LPV系統(tǒng)設(shè)計(jì)控制器有以下幾個(gè)優(yōu)點(diǎn)：設(shè)計(jì)控制器時(shí)無(wú)需再考慮如何插值；利用時(shí)變參數(shù)的測(cè)量值來(lái)提高控制性能；由于設(shè)計(jì)過(guò)程可以通過(guò)直接的方式處理參數(shù)集，故能從理論上保障系統(tǒng)的魯棒穩(wěn)定性以及其他性能要求。

目前，LPV系統(tǒng)的魯棒變?cè)鲆婵刂频难芯亢蛻?yīng)用范圍十分廣泛，如導(dǎo)彈[10-11]、無(wú)人機(jī)[12]等，但是，將LPV系統(tǒng)引入航天器姿態(tài)控制領(lǐng)域處理容錯(cuò)問(wèn)題的成果不是很多。文獻(xiàn)[13]針對(duì)衛(wèi)星執(zhí)行機(jī)構(gòu)發(fā)生乘性故障，將失效因子作為時(shí)變參數(shù)并進(jìn)行具有重疊特性的區(qū)間劃分，最終建立姿態(tài)動(dòng)力學(xué)切換LPV系統(tǒng)。對(duì)每一個(gè)子系統(tǒng)設(shè)計(jì)相應(yīng)的變?cè)鲆孀涌刂破鳎刂破髟鲆嬉约白酉到y(tǒng)間的切換律均與時(shí)變參數(shù)有關(guān)。而本文考慮轉(zhuǎn)動(dòng)慣量隨時(shí)間變化并將轉(zhuǎn)動(dòng)慣量作為時(shí)變參數(shù)，將失效因子作為已知上下界且未知的不確定時(shí)變參數(shù)，最終建立航天器姿態(tài)動(dòng)力學(xué)的仿射參數(shù)依賴不確定LPV模型。基于LPV模型設(shè)計(jì)控制器時(shí)，為保證不確定系統(tǒng)的魯棒性引入了保性能控制，為降低控制算法的保守性利用了仿射二次穩(wěn)定的方法。在航天器姿態(tài)控制系統(tǒng)中進(jìn)行仿真，結(jié)果表明控制算法的有效性。

1 航天器執(zhí)行機(jī)構(gòu)故障的姿態(tài)動(dòng)力學(xué)LPV模型

1.1航天器姿態(tài)動(dòng)力學(xué)系統(tǒng)模型

因衛(wèi)星所處環(huán)境復(fù)雜，燃料消耗，結(jié)構(gòu)改變，溫度變化，輻射等均會(huì)使衛(wèi)星的轉(zhuǎn)動(dòng)慣量發(fā)生改變，可靠有效的姿態(tài)控制需要考慮航天器轉(zhuǎn)動(dòng)慣量變化。因此，本文在建立航天器姿態(tài)動(dòng)力學(xué)模型時(shí)，假設(shè)轉(zhuǎn)動(dòng)慣量隨時(shí)間變化。

工程上常用的姿態(tài)描述法是歐拉角。在歐拉角姿態(tài)表示法中，最常用的是按zxy順序，相應(yīng)的轉(zhuǎn)角依次記為ψ、φ、ξ分別稱為滾動(dòng)角、俯仰角和偏航角。忽略轉(zhuǎn)動(dòng)慣量矩陣Ib中的慣量積，姿態(tài)動(dòng)力學(xué)方程可以寫(xiě)成

(1)

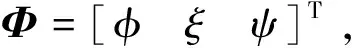
(2)

式中：

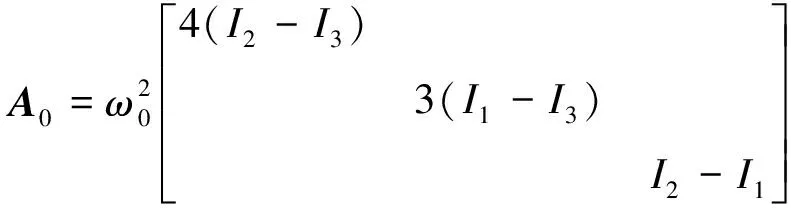
A2=Ib，Gu=E3，En為n維單位矩陣。

(3)

1.2航天器姿態(tài)動(dòng)力學(xué)LPV模型

對(duì)于LPV系統(tǒng)

(4)

當(dāng)A(θ)和B(θ)具有如下仿射參數(shù)依賴形式時(shí)，系統(tǒng)(4)便是仿射參數(shù)依賴LPV模型。

(5)

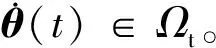
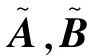
(6)

(7)

式中:θik∈[0,1]，Aik,Bik的表達(dá)式如下

(8)

(9)

令θik在整個(gè)控制過(guò)程中的變化范圍是

(10)

則

(11)

故

(12)

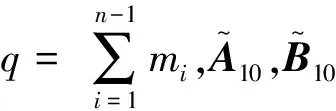
注1. 由式(12)得到的LPV系統(tǒng)，時(shí)變參數(shù)的變化范圍是θik∈[0,1]，將式(12)經(jīng)過(guò)簡(jiǎn)單的變換便可以得到時(shí)變參數(shù)在任何范圍內(nèi)變化的LPV系統(tǒng)。

1.3航天器執(zhí)行機(jī)構(gòu)故障的姿態(tài)動(dòng)力學(xué)LPV模型

執(zhí)行機(jī)構(gòu)的乘性故障是指輸出與輸入有一定倍數(shù)關(guān)系，可以表示為

uf=Gu

(13)

式中:u∈Rm為控制矢量，G表示故障對(duì)執(zhí)行機(jī)構(gòu)的影響，為

G=diag(g1,g2,…,gm),gi∈[0,1]

(14)

式中:gi為乘性故障失效因子，當(dāng)gi=1時(shí)執(zhí)行機(jī)構(gòu)正常運(yùn)行，gi=0時(shí)執(zhí)行機(jī)構(gòu)完全失效。

考慮航天器姿態(tài)控制中，執(zhí)行機(jī)構(gòu)采用三個(gè)正交安裝的反作用飛輪，則

G=diag(g1,g2,g3)=g1e11+g2e22+g3e33

(15)

將式(13)、式(15)、式(12)代入式(3)，得到執(zhí)行機(jī)構(gòu)發(fā)生乘性故障時(shí)的LPV模型，即

(16)

(17)

(18)

2 魯棒變?cè)鲆鍼ID容錯(cuò)控制

2.1問(wèn)題的描述

引入魯棒變?cè)鲆鍼ID控制器:

(19)

KP,KI,KD可表示為仿射參數(shù)依賴的形式，即

(20)

(21)

(22)

(23)

引入仿射參數(shù)依賴Lyapunov函數(shù)

(24)

(25)

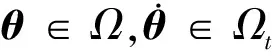
(26)

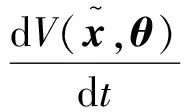
(27)

成立，則閉環(huán)系統(tǒng)(21)是仿射二次穩(wěn)定的。

對(duì)系統(tǒng)(3)為了保證保性能性，定義二次性能指標(biāo)

(28)

式中:Q=QT≥0,Rgt;0,S=ST≥0。

定義2. 對(duì)系統(tǒng)(16)和性能指標(biāo)(28)，如果存在一個(gè)控制律u*(t) 和一個(gè)正數(shù)J*，使得對(duì)所有允許的情況，閉環(huán)系統(tǒng)是漸近穩(wěn)定的，且閉環(huán)性能指標(biāo)滿足J≤J*，則J*稱為系統(tǒng)(16)的一個(gè)性能上界，u*(t)稱為系統(tǒng)(16)的一個(gè)保性能控制器。

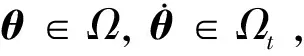
2.2魯棒變?cè)鲆鍼ID容錯(cuò)控制的設(shè)計(jì)

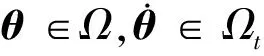
(29)

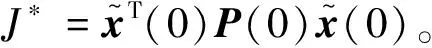
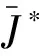
(30)

(31)

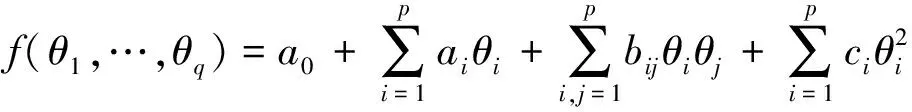
在研究魯棒變?cè)鲆鍼ID容錯(cuò)控制的過(guò)程中，受到了文獻(xiàn)[14-15]的啟發(fā)，完成了相應(yīng)容錯(cuò)控制器的設(shè)計(jì)。

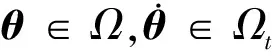
(32)

證. 引入輔助矩陣N1,N2，由式(21)和式(22)得

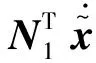
(33)

式(27)可以寫(xiě)為

(34)

同時(shí)

(35)

(36)

注2. 魯棒變?cè)鲆鍼ID容錯(cuò)控制的設(shè)計(jì)，最終轉(zhuǎn)化為雙線性矩陣不等式組可行解的問(wèn)題，故本文利用了Tomlab優(yōu)化工具箱中的PenBMI求解器。

注3. 令Fi=0,Fdi=0，根據(jù)定理1所求得的控制u(t)就是保證閉環(huán)系統(tǒng)仿射二次穩(wěn)定的保性能PID容錯(cuò)控制器。即傳統(tǒng)的PID容錯(cuò)控制是一種特殊的魯棒變?cè)鲆鍼ID容錯(cuò)控制。

3 仿真校驗(yàn)

仿真中，假定航天器初始時(shí)的轉(zhuǎn)動(dòng)慣量為I0=diag(200,100,300) kg·m2，在10≤t≤110 s勻速改變到If=diag(120,150,90) kg·m2，如圖1所示。

求解控制器時(shí)，令n=2，m1=1，根據(jù)式(8)、式(9)、式(12)，引入一個(gè)時(shí)變參數(shù)θ1∈[-1,1]，如圖2所示。對(duì)于在軌運(yùn)行的航天器而言，主要控制的目標(biāo)為盡量減少燃料消耗[14,16]，因而選取的Q、S、和R為Q=0.1E6,R=E3,S=0.001E6。令gi∈[0.3,1],i=1,2,3，根據(jù)式(16)和定理1，本文分別求解了使閉環(huán)系統(tǒng)仿射二次穩(wěn)定的保性能PID容錯(cuò)控制器和魯棒變?cè)鲆鍼ID容錯(cuò)控制器。本文所采用的航天器仿真參數(shù)見(jiàn)表1。

(1) PID容錯(cuò)控制

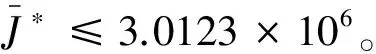
表1 航天器姿態(tài)仿真參數(shù)Table 1 Simulation parameters of spacecraft attitude control

圖3是飛輪無(wú)故障、在初始時(shí)刻發(fā)生故障1、故障2、故障3時(shí)，PID容錯(cuò)控制的仿真圖像。可知，4種情況系統(tǒng)均在200 s附近達(dá)到穩(wěn)定，飛輪在無(wú)故障以及發(fā)生乘性故障的情況下，閉環(huán)系統(tǒng)的穩(wěn)定性能相近，即PID容錯(cuò)控制是有效的。

(2)魯棒變?cè)鲆鍼ID容錯(cuò)控制

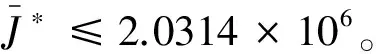
圖4是飛輪無(wú)故障、在初始時(shí)刻發(fā)生故障1、故障2、故障3時(shí)，魯棒變?cè)鲆鍼ID容錯(cuò)控制的仿真圖像。可知，在4種情況下，閉環(huán)系統(tǒng)均在150 s附近達(dá)到穩(wěn)定，閉環(huán)系統(tǒng)的穩(wěn)定性能相近，即魯棒變?cè)鲆鍼ID容錯(cuò)控制是有效的。

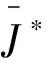
圖5是以偏航軸為例，系統(tǒng)達(dá)到穩(wěn)定后無(wú)故障、故障1、故障3時(shí)仿真對(duì)比圖像。由圖5可知，幾種情況下均能達(dá)到較高的控制精度，但是隨著故障程度的增加，控制精度略有降低。

PID容錯(cuò)控制是一種特殊的魯棒變?cè)鲆鍼ID容錯(cuò)控制，相當(dāng)于KPi=KIi=KDi=0，即PID容錯(cuò)控制的參數(shù)是固定不變的，不隨時(shí)變系統(tǒng)的變化而改變，因此，對(duì)于時(shí)變系統(tǒng)而言，PID容錯(cuò)控制的設(shè)計(jì)，增大了保守性，一定程度上犧牲了系統(tǒng)的性能。而魯棒變?cè)鲆鍼ID容錯(cuò)控制通過(guò)引入時(shí)變參數(shù)，降低了控制過(guò)程中的保守性，改善了系統(tǒng)的性能。另一方面，魯棒變?cè)鲆嫒蒎e(cuò)控制最終轉(zhuǎn)化為雙線性矩陣不等式可行解的問(wèn)題，故一定程度上增大了計(jì)算量。

4 結(jié) 論

對(duì)于航天器執(zhí)行機(jī)構(gòu)乘性故障的姿態(tài)容錯(cuò)控制，本文考慮轉(zhuǎn)動(dòng)慣量隨時(shí)間改變，將轉(zhuǎn)動(dòng)慣量信息作為實(shí)時(shí)可測(cè)的時(shí)變參數(shù)，失效因子作為不確定的時(shí)變參數(shù)，建立姿態(tài)動(dòng)力學(xué)的仿射參數(shù)依賴不確定LPV系統(tǒng)。魯棒變?cè)鲆嫒蒎e(cuò)控制的設(shè)計(jì)，利用仿射二次穩(wěn)定的方法降低算法的保守性和引入保性能控制保證不確定系統(tǒng)具有一定的魯棒性。仿真結(jié)果表明控制器是有效的。與PID容錯(cuò)控制相比，魯棒變?cè)鲆鍼ID容錯(cuò)控制器與時(shí)變參數(shù)有關(guān)，一定程度上改善了系統(tǒng)的性能。然而，變?cè)鲆鍼ID容錯(cuò)控制最終轉(zhuǎn)化為雙線性矩陣不等式可行解的問(wèn)題，增加了控制器求解的復(fù)雜度。

[1] Tafazoli M. A study of on-orbit spacecraft failures[J]. Acta Astronautica, 2009, 64(2): 195-205.

[2] 賈慶賢, 張迎春, 陳雪芹, 等. 衛(wèi)星姿態(tài)控制系統(tǒng)故障重構(gòu)觀測(cè)器設(shè)計(jì)[J]. 宇航學(xué)報(bào), 2016, 37(4): 442-450.[Jia Qing-xian, Zhang Ying-chun, Chen Xue-qin, et al. Observer design for fault reconstruction in satellite attitude control system[J]. Journal of Astronautics, 2016, 37(4): 442-450.]

[3] Zhang A, Hu Q, Zhang Y. Observer-based attitude control for satellite under actuator fault[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(4): 806-811.

[4] Li D, Lei J. Fault-tolerant attitude control of spacecraft by using robust adaptive method[C]. IEEE International Conference on Electronic Measurement amp; Instruments, Qingdao, China, July 16-18, 2015.

[5] Zhou Z, Gao Z, Xu Y, et al. Fault tolerant attitude control design for rigid satellite using sliding mode observer technique[C]. IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, August 12-14, 2016.

[6] Jiang Y, Hu Q, Ma G. Adaptive back stepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures[J]. ISA Transactions, 2010, 49(1): 57-69.

[7] Xiao B, Hu Q, Zhang Y, et al. Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 838-849.

[8] 管宇. 衛(wèi)星姿態(tài)控制系統(tǒng)的故障診斷與容錯(cuò)方法研究[D]. 哈爾濱: 哈爾濱工業(yè)大學(xué), 2012.[Guan Yu. Research on fault diagnosis and fault-tolerant control of satellite attitude control system[D]. Harbin: Harbin Institute of Technology, 2012.]

[9] 袁士春. 船舶運(yùn)動(dòng)與主推進(jìn)線性變參數(shù)聯(lián)合控制的研究[D]. 大連: 大連海事大學(xué), 2007.[Yuan Shi-chun. Integrated control of ship motion and main engine propulsion based on linear parameter-varying[D]. Dalian: Dalian Maritime University, 2007.]

[10] Mehrabian A R, Roshanian J. Design of gain-scheduled autopilot for a highly-agile missile[C]. International Symposium on Systems and Control in Aerospace and Astronautics, Harbin, China, January 19-21, 2006.

[11] Yu J, Li L, Zhao H, et al.Robust gain-scheduled controller design for air defense missile[C]. Chinese Control Conference, Harbin, China, August 7-11, 2006.

[12] Natesan K, Gu D W, Postlethwaite I, et al. Design of flight controllers based on simplified LPV model of a UAV[C]. IEEE Conference on Decision and Control, San Diego, CA, USA, December 13-15, 2006.

[13] He X, Zhang W,Leng Y, et al. Fault tolerant control with switched LPV method based on hysteresis strategy and an application to a microsatellite model[C]. The 34th Chinese. IEEE Control Conference, Hangzhou, China, July 28-30, 2015.

[14] Vesely V, Ilka A. Gain-scheduled PID controller design[J]. Journal of Process Control, 2013, 23(8): 1141-1148.

[15] Vesely V, Ilka A. Robust gain-scheduled PID controller design for uncertain LPV systems[J]. Journal of Electrical Engineering, 2015, 66(1): 19-25.

[16] 馬清亮, 楊海燕, 岳瑞華, 等. 空間飛行器大角度姿態(tài)機(jī)動(dòng)最優(yōu)保性能控制[J]. 空間控制技術(shù)與應(yīng)用, 2013, 39(3): 8-13.[Ma Qing-liang, Yang Hai-yan, Yue Rui-hua, et al. Optimization control of spacecraft large angle attitude maneuvers[J]. Aerospace Control and Application, 2013, 39(3): 8-13.]

SpacecraftAttitudeFaultTolerantControlwithActuatorFault

GENG Yun-hai, JIN Rong-yu, CHEN Xue-qin, LI Dong-bai

(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150001，China)

For spacecraft attitude control with actuator (flywheel) fault, robust gain-scheduled PID fault tolerant control is designed based on linear parameter varying (LPV) system. Considering the inertia changing and actuator multiplicative fault, the spacecraft attitude dynamics can be rewritten as an uncertain LPV system. The conservation of the controller algorithm is reduced by affine quadratic stability and the robust performance is ensured by guaranteed cost control. The simulation results show the effectiveness of the controller.

Spacecraft attitude control; Fault tolerant control; Actuator fault; Linear parameter varying (LPV); Robust gain-scheduled control

V448.2

A

1000-1328(2017)11- 1186- 09

10.3873/j.issn.1000- 1328.2017.11.007

2017- 07- 03;

2017- 09- 14

微小型航天器技術(shù)國(guó)防重點(diǎn)學(xué)科實(shí)驗(yàn)室開(kāi)放基金(HIT.KLOP.MST.201603); 國(guó)家重點(diǎn)研發(fā)計(jì)劃(2016YFB0500901)

耿云海(1970-)，男，博士，教授，主要從事航天器姿態(tài)動(dòng)力學(xué)與控制研究。

通信地址：哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所(150001)

電話：18645115250

E-mail：gengyh@hit.edu.cn

陳雪芹(1982-)，女，副研究員，主要從事航天器姿態(tài)控制研究。本文通信作者。

通信地址：哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所(150001)

電話：18500218686

E-mail：cxqhit@163.com