一種用于重復數據刪除的非對稱最大值分塊算法研究

郭玉劍，曾志浩

(湖南工業大學 計算機學院，湖南 株洲 412000)

一種用于重復數據刪除的非對稱最大值分塊算法研究

郭玉劍，曾志浩

(湖南工業大學 計算機學院，湖南 株洲412000)

分塊是一種將文件劃分成更小文件的過程，該方法被廣泛應用在重復數據刪除系統中。針對傳統的基于內容分塊(CDC)中面臨的高額計算開銷問題，提出了一種稱為非對稱最大值的分塊算法(CAAM)。采用字節值代替哈希值來聲明切點，利用固定大小窗口和可變大小窗口來查找作為切點的最大值，并且允許在保留內容定義分塊(CDC)屬性的同時進行較少的計算開銷。最后將CAAM與現有的基于散列和無哈希的分塊算法進行了比較，實驗結果表明，CAAM算法比其他算法具有更低的計算開銷和更高的分塊吞吐量。

重復數據刪除；非對稱窗口；內容定義分塊；無哈希分塊；切點

0 引言

根據國際數據公司(IDC)的調查研究，2013年全球數字信息產生量約為4.4 ZB，到2020年將達到44 ZB[1]，如何有效地存儲和傳輸如此海量的數據對技術人員提出了巨大的挑戰。然而，最近的研究表明數據倉庫中存在大量的重復數據[2]。因此，一種高效的降低存儲冗余的無損壓縮技術——重復數據刪除，成為解決這一難題的重要方法之一。由于顯著的數據縮減率，塊級去重被應用于各種領域，例如存儲系統[3-4]、文件傳輸系統[5]和遠程文件系統[6]。

基于塊級的重復數據刪除方案是將數據流分解成多個數據塊，并且散列每個塊，其中使用散列函數生成各個數據塊的指紋，在新的數據流進入存儲系統之前，先通過分塊算法將其分解成多個數據塊，然后通過對比新數據塊的數據指紋來確定是否存儲。從這個過程中可以看出，重復數據刪除必經過四個階段，即分塊、指紋、索引和寫入。而分塊作為重復數據刪除的第一個關鍵階段，如何選擇有效的分塊算法成為重復數據刪除中一個重要難題。

基于Rabin指紋的內容定義分塊(CDC)算法[7]是最著名的分塊算法之一。這種方法使用Rabin滾動哈希來尋找切割點，它解決了固定長度分塊中關于字節移位的問題。但是由于滾動哈希是在滑動窗口移動過程中計算哈希值，因此這種算法在散列過程中需要消耗大量時間計算哈希值。不同于Rabin分塊算法，BJ?RNER N等人提出的局部最大算法(LMC)[8]是利用文件和滑動窗口的字節值來確定切割點，雖然這種方法不需要哈希計算，但是它需要比較每個字節來進行分塊。文獻[9]中提出的基于非對稱極值(AE)的內容分塊算法，使用固定窗口和可變大小的窗口來確定切割點，其中極值位于兩個窗口之間。不同于局部最大算法，AE算法不需要使用滑動窗口來確定切割點，因此該算法只需要很少的字節比較。盡管相對于LMC算法來說AE算法的比較次數較少，但是仍然需要高額的計算量。

針對分塊中需要大量計算開銷的問題，本文提出了一個基于非對稱最大的分塊算法(CAAM)。該算法與AE算法類似，使用兩個窗口：固定長度窗口和可變長度窗口。與AE算法不同，CAAM算法對窗口使用了不同的位置。窗口位置從固定長度窗口開始，然后是可變大小的窗口和最大的字節。切割點位于塊的末尾。這種配置一定程度上減少了比較次數，而且在重復數據刪除吞吐量方面也優于AE算法。

1 背景與挑戰

1.1背景

大部分數據壓縮技術都是采用分塊，例如，重復數據刪除、遠程差分壓縮。重復數據刪除的工作原理就是利用這種方法來消除文件與文件之間的重復數據。在重復數據刪除中，分塊算法是實現高去重率的一種重要方法。通過選擇正確的分塊算法，可以節省消重時間和硬件空間。

分塊可以被分成兩類：(1)基于文件的分塊；(2)基于數據塊的分塊。基于文件的分塊意味著將整個文件視為一個數據塊，而基于數據塊的分塊是將文件劃分成多個塊。當文件被分割成塊時，塊大小可以是固定長度大小，也可以是可變長度大小。固定長度分塊具有分塊速度優勢，但是當數據流有n個字節插入時，之后的所有數據都會偏移n個字節。在進行數據分塊時，這n字節之后的數據塊就會變成新的數據塊，這樣必然大大降低重復數據刪除率。基于內容的分塊(CDC)是通過將文件分成可變大小的數據塊來解決字節移位問題的，該算法通過利用文件內部的特征來找到切點，因此當文件移位時，只有幾個塊受影響。CDC與固定長度分塊相比，具有更高的消重率。

CDC允許使用任何根據文件內部特征條件來發現切割點。例如在基于散列的分塊算法中，它是根據滑動窗口和散列函數來發現切割點。而文獻[8-9]提出的算法都是根據字節值來尋找切割點。除了利用散列和字節來確認切割點，神經網絡和機器學習也被用來尋找切割點，但是它們的計算開銷遠高于利用散列和字節的方法來找到切割點。

分塊算法在重復數據刪除系統中具有決定性的作用，但是塊管理也是重復數據刪除中的一個重要環節，當數據塊逐步增多時，塊的索引也將成為一大難題。近年有許多關于塊索引的研究，其中主要集中在利用緩存[10-11]、布隆過濾器[12]或者布谷鳥過濾器[13]等來減少數據塊搜索時間。

1.2挑戰

相較于固定大小分塊，CDC分塊擁有更多的優點。然而，CDC分塊算法在處理數據流程中稍微消耗時間，特別是對于處理能力相對較小的設備，例如移動設備和物聯網服務等。在之前的工作中，一般采用的是基于Rabin的分塊算法來消除重復數據。但這種方法在移動應用時需要大量的處理時間。

在討論和評價各個分塊算法性能時，需要聲明三個用于評價算法的標準：

(1)內容依賴：分塊算法應該根據文件內容的內在特征來定義切點。這樣可以抵抗字節移位，而且可以在海量數據消除更多重復數據。

(2)較低的塊大小差異：依據算法產生的塊需要有較低的塊大小差異，因為塊大小差異很大程度上影響著重刪率。為了限制塊大小差異，需要限制塊的最大或者最小值。然而，這樣做卻影響了算法基于內容依賴的屬性，并且也不能有效抵抗字節移位。

(3)高吞吐量和重復檢測：分塊算法應該在重復數據刪除效率和計算開銷兩者中保持良好的平衡。

2 基于非對稱最大分塊算法設計

為了實現低計算開銷和字節移位抗性算法的目標，在AE算法的基礎上提出了基于非對稱最大算法(CAAM)。與AE算法類似，CAAM也使用兩個窗口：固定大小窗口和可變大小窗口。但是窗口的放置位置和AE算法不同。在CAAM算法中固定窗口位于塊的開始處，然后是可變窗口和最大字節值。

CAAM算法首先在固定窗口中尋找最大字節值，如果緊接固定窗口的字節比固定窗口所有值都要大，則該值便作為最大值字節，同時切點也被確定。否則，算法繼續移動到下個字節，直到找到最大值為止。因此算法的最小塊的大小是w+1，其中w是固定窗口大小。查找切點的偽代碼具體如下：

輸入：input string,Str;length of the string,L;

輸出：cut-point I;

Predefinedvalued:window size,w;

FunctionCAAMChunkning (Str,L)

i=1;

while(ilt;L)

if Str[i].valuegt;=max.value then

if igt;w then

return i

end if

max.value=Str[i].value

max.position=i

end if

i=i+1

end while

end function

在上述算法中詳細說明了CAAM算法中的分塊細節。從該算法可以看出，CAAM通過在固定窗口中尋找到最大值來減少計算時間。而AE算法是需要先通過尋找最小值，然后再計算切點的位置，在此過程中就需要更多的計算開銷。

為了更好地展示每個算法是如何工作的，通過圖1中的示例來詳細說明。其中規定使用相同的字節流，定義總字節數為14，窗口大小設定為5位。基于Rabin的分塊算法中滑動窗口從塊的開始處向后開始滑動，如圖1(a)所示。在該示例的開頭，滑動窗口的內容為0×89504EA10D。如果窗口的哈希值與預定值不匹配，則左移窗口，滑動到下個字節，直到窗口的哈希值與預定值匹配為止。在圖1(a)的示例中，0×0D0A1AEA48的哈希值與預定值相匹配，從而最終確定切點位置為0×48右側。

LMC算法和基于Rabin的分塊算法類似，同樣使用滑動窗口，如圖1(b)所示。其中滑動窗口是由兩個固定大小窗口組成的，當發現位于兩個窗口中間的字節大于窗口中所有字節時，切點位置便是窗口中間最大值的位置。

表1 測試中使用的數據集

與LMC算法不同，AE算法需要掃描每個字節來找到切點，如圖1(c)所示。在AE算法中，固定窗口始終位于待掃描字節的右側。AE算法從字節流的左側依次往右開始掃描，并將掃描的字節值與固定窗口中的所有字節進行比較。當字節大小大于固定窗口中的所有字節時，則確定切點。由此可見，當第一個字節滿足條件時，可變窗口的值是0字節。在圖1(c)的示例中，算法從0×89掃描到0×EA時發現切點，因為0×EA大于固定窗口中的任何字節。其中確認切點位于固定窗口的右側。

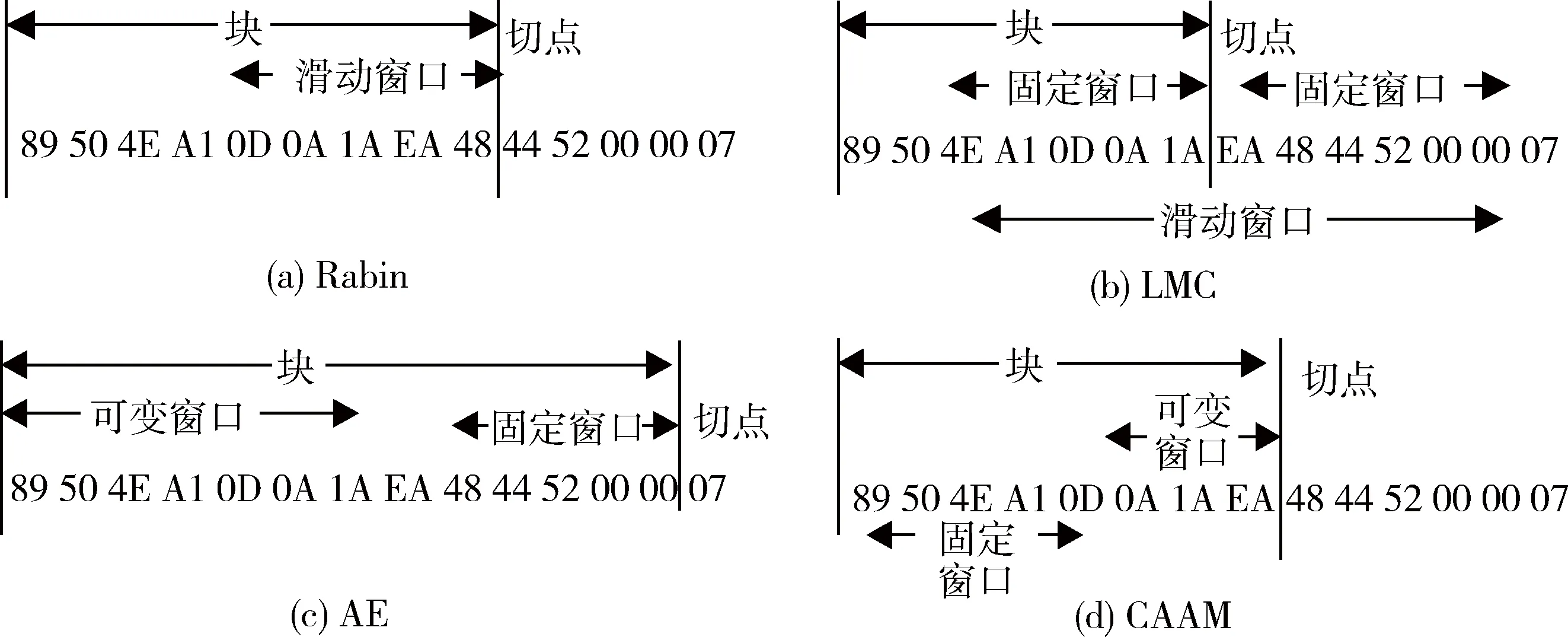
圖1 Rabin、LMC、AE和CAAM算法的工作示意圖

CAAM算法也需要逐字掃描每個字節與窗口中的最大值相比較。CAAM通過查找到固定窗口中的最大值來啟動。在圖1(d)中可以看出，固定窗口中的最大值是0×A1。等到算法掃描完固定窗口后，將窗口后的每個字節與窗口中的最大值相比較。當掃描到的某個字節大于固定窗口中的最大字節時，則說明找到切點。從圖中可以看出，0×EA是切割點。

表2 被發現的重復數據量

3 實驗分析

3.1實驗環境

實驗將基于Rabin的分塊算法、LMC算法、AE算法和CAAM算法做比較，評估CAAM算法的分塊吞吐量和重刪率。硬件環境：主機為CPU Intel i7 6700 3.6 GHz，4核8線程，12 GB DDR4,2 133 MHz和三星850 Evo 256GB SSD。SSD通過SATA3接口連接。實驗采用三種不同形式的數據集，第一個數據集是由多個Linux發行版的編譯，它們在每個文件中的不同位置都有大量的重復數據。第二個數據集是由10個23 min的H.264編碼視頻組成的。第三個數據集是來自網絡的轉儲文件。詳細信息如表1所示。

3.2分塊吞吐量對比

本節通過分塊吞吐量和每秒保存的字節(BSPS)來評估三個算法之間的分塊性能。分塊吞吐量是根據原始數據集的大小與分塊時間的比值得到的，而每秒保存的字節是根據被找到的重復數據除以原始數據集，最后乘以分塊吞吐量得到的。具體公式如下：

通過實驗結果表明，與其他算法相比，CAAM算法具有更高的吞吐量。雖然在三種數據集中發現重復數據的數量上，CAAM算法要略低于AE算法，如表2所示。但是CAAM算法在分塊吞吐量上要比AE算法高出42%～49%，如圖2、3所示。而且從數據集的處理時間上來看，CAAM算法也要優于其他算法，如表3所示。總體而言，CAAM在吞吐量方面要優于其他算法。

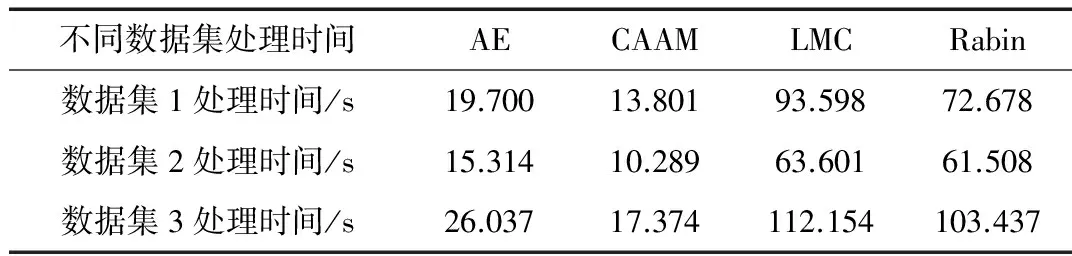
表3 不同數據集處理時間

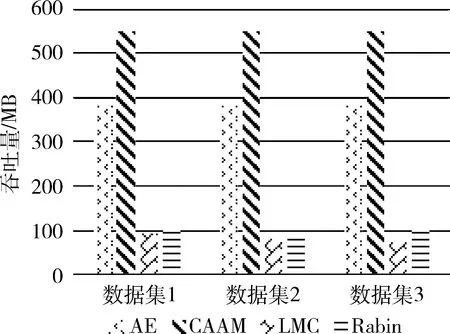
圖2 四種算法的分塊吞吐量

圖3 四種算法在不同數據集下每秒保存的字節數

4 結論

本文分別討論了Rabin算法、LMC算法和AE算法三種算法的分塊過程，并分析了它們的分塊性能。針對它們在分塊吞吐量上的低效率問題，提出了一種新的分塊算法——基于非對稱的最大值分塊算法(CAAM)。本文利用三種不同類型的數據集進行了實驗。實驗證明，與其他分塊算法相比，CAAM具有更低的計算開銷和高分塊吞吐量。本方法還有一些未解決的問題，例如：在分塊之前如何確定固定窗口的大小，研究固定窗口大小對分塊的影響將是接下來的工作之一。

[1] VERNON T. The digital universe of opportunities: rich data and the increasing value of the internet of things[EB/OL].(2014-04-10)[2017-02-14] https://www.emc.com/leadership/digital-universe/2014iview/executive-summary.htm.

[2] QUINLAN S,DORWARD S. Awarded best paper!-venti: a new approach to archival data storage[C].Proceedings of the 1st USENIX Conference on File and Storage Technologies. USENIX Association, 2002:89-101.

[3] Zhang Xuecheng, Deng Mingzhu. An Overview on Data Deduplication Techniques[M].Berlin: Springer International Publishing, 2017.

[4] 孫虎威, 靳嘉偉, 張晶,等. 重復數據刪除算法在VTL系統中的應用研究[J]. 微型機與應用, 2013, 32(6):82-85.

[5] 顧瑜, 劉川意, 孫林春,等. 帶重復數據刪除的大規模存儲系統可靠性保證[J]. 清華大學學報(自然科學版), 2010(5):739-744.

[6] SANADHYA S, SIVAKUMAR R, KIM K H, et al. Asymmetric caching: improved network deduplication for mobile devices[C].International Conference on Mobile Computing and Networking. ACM, 2012:161-172.

[7] RABIN M O. Fingerprinting by random polynomials[J]. Center for Research in Computing Technology, 1981,15(81): 15-18.

[8] BJ?RNER N, BLASS A, GUREVICH Y. Content-dependent chunking for differential compression, the local maximum approach[J]. Journal of Computer amp; System Sciences, 2010, 76(3):154-203.

[9] Zhang Yucheng, Feng Dan, Jiang Hong, et al. A fast asymmetric extre-mum content defined chunking algorithm for data deduplication in backup storage systems[J]. IEEE Tran-sactions on Computers,2017,66(2):199-211.

[10] DUTTA P,PATTNAIK P, SAHU R K. Brushing—an Algorithm for data deduplication[M]. Information Systems Design and Intelligent Applications. Springer India, 2016.

[11] Zhou Bing, Wen Jiangtao. Metadata feedback and utilization for data deduplication across WAN[J]. Journal of Computer Science and Technology, 2016, 31(3): 604-623.

[12] 張宗華,屈英, 葉志佳,等. 基于多特征匹配和Bloom filter的重復數據刪除算法[J]. 深圳大學學報(理工版), 2016, 33(5):531-535.

[13] BEHLING M, LAVERGNE J. Lubuntu[CP/OL]. (2016-10-15)[2016-10-20]http://lubuntu.net/.

[14] VINET J, GRIFFIN A, Arch Linux[CP/OL]. (2016-10-15)[2016-10-20]https://www.archlinux.org/download/.

[15] Google. Chromium OS[CP/OL].(2016-10-15)[2016-10-20]https://www.chromium.org/chromiumos.

[16] SHUTTLEWORTH M. Ubuntu[CP/OL].(2016-10-15)[2016-10-20]https://www.ubuntu.com/download/desktop。

2017-04-30)

郭玉劍(1991-)，通信作者，男，碩士，主要研究方向：大數據處理技術及應用。E-mail:1436066470@qq.com。

曾志浩(1975-)，男，博士，講師，主要研究方向：面向Web服務的軟件開發方法、大數據處理技術。

Research on an asymmetric maximum chunking algorithm for deduplication

Guo Yujian, Zeng Zhihao

(College of Computer Science, Hunan University of Technology, Zhuzhou 41200, China)

Chunking is a process of spilting files into smaller files, which is widely used in deduplication systems. Aiming at the problem of high computational overhead in traditional content-based chunking (CDC), a new chunking algorithm called asymmetric maximum (CAAM) is proposed. Instead of using hashes,CAAM uses the byte value to declare the cut points. The algorithm utilizes the fixed size window and the variable size window to find the maximum value which is cut points. The algorithm allows less computation overhead while keeping the CDC property. Finally, the CAAM algorithm is compared with the existing hash-based and hash-less. The experimental results show that the CAAM algorithm has lower computational cost and higher chunking throughput than other algorithms.

deduplication; asymmetric window; content-defined chunking; hash-less chunking; cut points

TP391

A

10.19358/j.issn.1674- 7720.2017.22.009

郭玉劍，曾志浩.一種用于重復數據刪除的非對稱最大值分塊算法研究J.微型機與應用，2017,36(22)：30-33.