Jacobi迭代法與Gauss-Seidel迭代法

郝艷花

（山西大同大學數學與計算機科學學院,山西大同037009）

Jacobi迭代法與Gauss-Seidel迭代法

郝艷花

（山西大同大學數學與計算機科學學院,山西大同037009）

迭代法是解線性方程組的一個很重要的方法，特別是在系數矩陣為稀疏矩陣的大型線性方程組中尤為重要。主要討論解線性方程組的雅可比迭代法與高斯-塞德爾迭代法這兩種方法,針對這兩種迭代法的定義，收斂性，以及收斂速度展開討論。

線性方程組；雅可比迭代法；高斯-塞德爾迭代法；收斂性

目前在工程技術、物理學、生物學以及自然科學中很多問題的解決經常歸結為解線性代數方程組，例如用有限元或者差分法解常微分方程，偏微分方程邊值問題，用最小二乘法求實驗數據的曲線擬合，經濟學中的投入-產出分析以及增長模型等問題都導致求解線性代數方程組，而這些方程組中的未知量往往多達幾百個，用傳統方法求解顯然很復雜，只能借助計算機。

目前關于線性方程組的數值解法一般有兩類：迭代法和直接法。直接法是經過有限布算術運算，可求得線性方程組精確解的方法，但是在實際問題中存在舍入誤差以及它的影響，這種方法只能求得線性方程組的近似解。而相對于直接法，迭代法是用某種極限過程逐步逼近線性方程組精確解的方法，它具有需要程序設計簡單，計算機的存儲單元較少，原始系數矩陣在計算過程中一直不變等優點，但存在收斂性和收斂速度等問題。[1-2]本文主要討論解線性方程組的雅可比迭代法與高斯-塞德爾迭代法的收斂性。[3-4]

1 迭代法的基本概念

1.1 迭代法的定義

定義1對于給定的線性方程組x=Ax+f,設有唯一解x*，則x*=Ax+f，又設x(0)為認取的初始向量，按以下公式構造向量序列x(k+1)=Ax(k)+f,k=0,1,2,…,其中k表示迭代次數。

定義2對于給定的線性方程組x=Ax+f，用逐步代入求近似解的方法稱為迭代法。

2 迭代法的收斂性

設有線性方程組,Ax=b，其中A=aij∈Rn×n為非奇異矩陣，下面研究建立解Ax=b的迭代法。

將A分裂為A=E-F，其中E為可選擇的非奇異矩陣，且Ex=b容易求解，稱E為分裂矩陣。于是，求解Ax=b轉化為求解Ex=Fx+b，即求解

即解線性方程組

從而可構造一階定常迭代法：

其中B=E-1F=E-1(E-A)=I-E-1A,f=E-1b,稱B為迭代法的迭代矩陣，選取E矩陣，就得到解Ax=b的各種迭代法。

定理1（迭代法收斂的充分條件）設有線性方程組x=Bx+f及一階定常x(k+1)=Bx(k)+f,如果有B的某種算子范數‖B‖=q＜1，則

（1）迭代法收斂，即對任意的x(0)有且x*=Bx(k)+f；

定理2（迭代法收斂的充要條件）給定線性方程組（1）以及一階定常迭代法，對任意選取的初始向量x(0)，迭代法（2）式收斂的充要條件是矩陣B的譜半徑ρ(B)＜1。

證明必要性:設對任意選取的x(0)，有其中x(k+1)=Bx(k)+f。

顯然，極限x*是線性方程組（1）的解，且誤差向量ε(k)=x(k)-x*=Bε(k-1)=…=Bkε(0)→0(k→∞)，

充分性：設ρ(B)＜1,易知Ax=f(A=I-B)唯一解，記為x*，則x*=Bx*+f，誤差向量ε(k)=x(k)-x*=Bkε(0),ε(0)=x(0)-x*。設ρ(B)＜1 ，所以有0，于是對任意x(0)，有即

3 迭代法的收斂速度

定義4一階定常迭代法

解:先求迭代矩陣B0的特征值，由特征方程

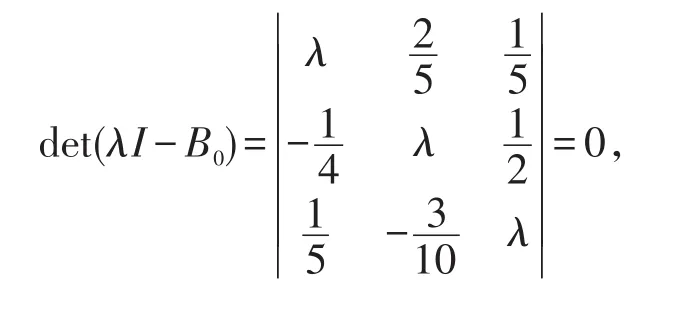
解得λ1,λ2,λ3，所以ρ(B0)＜1,所以用該迭代法解此線性方程組是收斂的。

例2考察用迭代法解線性方程組x(k+1)=Bx(k)+f的收斂性，其中

解：特征方程為 det(λI-B)=λ2-5λ+4=0，所以λ1=1,λ2=4，即ρ(B)≥ 1,所以由迭代法收斂的充要條件，得用此迭代法解該線性方程組不收斂。

4 雅可比迭代法與高斯-塞德爾迭代法及其收斂性

4.1 高斯-塞德爾迭代法

將線性方程組Ax=b中的系數矩陣A=aij∈Rn×n分成三部分,

選取分裂矩陣E=D-L（下三角矩陣），A=E-F，于是由一階定常迭代法可以得到解Ax=b的高斯-塞德爾迭代法，

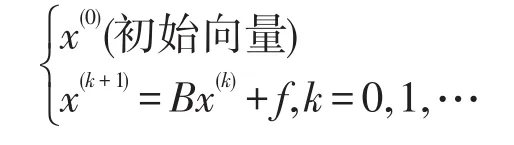
其中，稱G為Ax=b的高斯-塞德爾迭代法的迭代矩陣。

下面給出高斯-塞德爾迭代法的分量計算公式。

于是解Ax=b的高斯-塞德爾迭代法的計算公式為

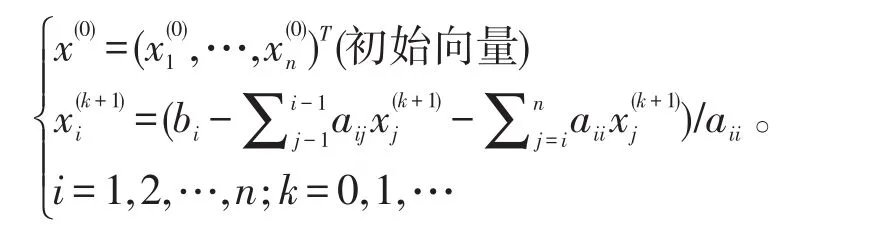
4.2 雅可比迭代法

選取分裂矩陣E=D（對角矩陣）A=D-F,同樣由一階定常迭代法得到解Ax=b的雅可比迭代法

其中B=1-D-1A=D-1(L+U)=J,f=D-1b稱J為解Ax=b的雅可比迭代法的迭代矩陣。

由雅可比迭代公式有

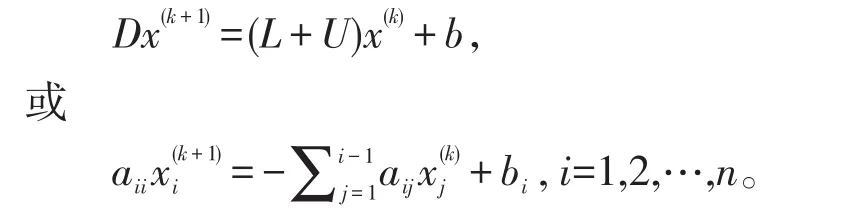
于是得到解Ax=b的雅可比迭代法的計算公式為

例3設線性方程組

分別寫出雅可比迭代法與高斯-塞德爾迭代法。

解：雅可比迭代為

高斯-塞德爾迭代法

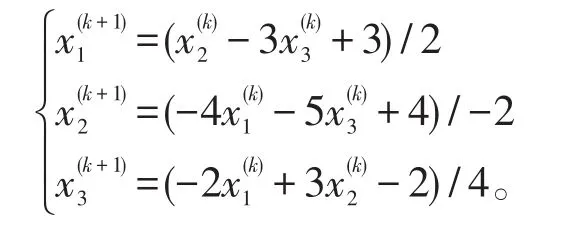
4.3 雅可比迭代法與高斯-塞德爾迭代法收斂性

由定理1得，高斯-塞德爾迭代法與雅可比迭代法收斂的充要條件分別是ρ(BG)＜1，其中G=(D-L)-1U，和ρ(BJ)＜1，其中J=D-1(L+U)。

由定理2得，高斯-塞德爾迭代法與雅可比迭代法收斂的充分條件是‖G‖＜1，其中G=(DL)-1U，和‖J‖＜1，其中J=D-1(L+U)。

另外，在實際問題的求解過程中，線性方程組Ax=b，其矩陣A經常具有某些特征。例如A為對稱正定矩陣，或為不可約矩陣，或者A具有對角占優性質等。下面討論當A具有這些性質時解線性方程組Ax=b的收斂性。

[1]李慶揚，王能超，易大義.數值分析[M].5版.北京：清華大學出版社.

[2]張傳林.數值方法[M].北京：中國科學文化出版社，2001：80-150.

[3]馬云.數值分析中的迭代法解線性方程組[J].考試周刊，2010（50）：71-72.

[4]趙丹.雅可比迭代法與高斯-塞德爾迭代法研究[J].興義民族師范學院學報,2012（2）：108-112.

〔責任編輯 高海〕

Jacobi Iteration Method and Gauss-Seidel Iteration Method

HAO Yan-Hua
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

Iteration method is a very important method for solving linear equations,especially in large linear equations with coeffi?cient matrices as sparse matrices.In this paper,we mainly discuss on the Jacobi iteration method and the Gauss-Seidel iteration meth?od for solving the linear equations.We mainly study the definition,convergence and convergence speed of these two iteration methods.

linear equations;Jacobi iteration;Gauss-Seidel iteration;astringency

TP273

A

1674-0874(2017)05-0003-03

2017-06-26

郝艷花（1974-），女，山西廣靈人，碩士，副教授，研究方向：計算數學。