基于微分平滑的欠驅動無人地面車輛的軌跡跟蹤控制
廣東工業大學 余 章
基于微分平滑的欠驅動無人地面車輛的軌跡跟蹤控制
廣東工業大學 余 章
本文針對具有非完整約束的欠驅動無人地面車輛(Unmanned Ground Vehicle,UGV)的軌跡跟蹤控制問題進行了探討。通過分析系統的運動模型證明了欠驅動UGV是微分平滑的。采用微分平滑理論設計了欠驅動UGV的一個參考軌跡。然后推導了使該參考軌跡的跟蹤誤差漸近收斂的控制律。最后通過仿真試驗驗證了文中方法的有效性。
欠驅動UGV;微分平滑;軌跡跟蹤
引言
無人地面車輛(Unmanned Ground Vehicle,UGV)是一種可以自動行駛并且攜帶工作載荷的地面移動平臺,能夠按照預先選擇的參考軌跡行駛到復雜或危險的地方,從而可以執行特定的任務。其特點是集環境感知、動態決策和規劃、行為控制與執行等多種功能于一體。目前,無人地面車輛(UGV)已經廣泛應用于生產生活的諸多領域,以幫助人們處理一些繁重的或危險的工作,如核電站災難發生后的搜索無人地面車輛[1]。
由于UGV只有2個控制輸入,但是它的平面運動具有3個自由度,因此UGV的軌跡跟蹤控制具有欠驅動特性。欠驅動系統的控制特點是可用較少的輸入來控制其在相對維數較高的廣義坐標空間內的運動。欠驅動系統在減輕重量、降低造價、節約能量以及增強系統靈活性等方面有其獨特的地方。
不同于全驅動控制,在欠驅動控制下不是所有運動軌跡都是可行的。Fliess和Levine等在文獻[2]中提出了微分平滑的概念。微分平滑系統對于規劃可行的參考軌跡很有作用,因為如果它的平滑輸出已知,則可以先在輸出空間中進行軌跡規劃,然后將可行軌跡通過代數運算映射到適當的輸入空間,再設計合理的軌跡跟蹤控制律來達到這個軌跡的跟蹤。后面將探討欠驅動UGV系統的平滑性及其平滑輸出,并利用微分平滑理論來得到欠驅動UGV的一個位姿參考軌跡。
滑模控制具有當系統進入滑動模態后對系統參數變化和外界干擾不敏感的優良特性,且控制器的設計過程簡潔,算法的運算量小,因此將被應用于后文的軌跡跟蹤控制系統的設計中。
1 無人地面車輛(UGV)的運動學模型

圖1 UGV的運動學模型
本文將以圖所示中的具有非完整約束的UGV為研究對象,該UGV有左右兩個驅動輪,以及一個起支撐作用的萬向隨動輪。兩個驅動輪各由一個電機來驅動,如果兩個電機的轉速不同,則兩個輪子會產生“差動”,從而可實現轉彎。由于萬向隨動輪只起支撐作用,既不掌舵也不產生推進力,因此在計算UGV運動學方程時萬向隨動輪可以被忽略,不會影響運動學方程。
該UGV的控制輸入為線速度υ和角速度ω,其狀態由左右兩個驅動輪的軸中點M(假設此點是UGV的中心)在慣性坐標系中的坐標位置(x, y)及姿態角θ來表示,其中姿態角為UGV的前進方向與X軸的夾角。
下面給出欠驅動UGV的運動學方程如下[3]:

由該運動學方程可見,具有非完整約束的UGV的運動學模型共有2個控制輸入(υ和ω),3個狀態輸出(x、y和θ),故該模型為欠驅動系統,可實現2個狀態的主動跟蹤,剩下的1個狀態則隨動或鎮定。后文將基于微分平滑理論來研究UGV的軌跡跟蹤問題,即通過設計軌跡跟蹤控制律(υ, ω)來實現UGV的參考位置(xr, yr)的跟蹤,并實現參考姿態角θr的鎮定。
2 無人地面車輛(UGV)的軌跡跟蹤控制的微分平滑特性及利用
前已述及,UGV是一個欠驅動系統,即系統控制輸入向量空間的維數小于系統廣義坐標向量空間的維數。為了后文的方便,先給出微分平滑的定義如下。
定義 針對非線性系統:

其中,x為狀態變量,u為控制變量。如果能夠找到一個輸出集合:
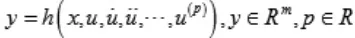
而且由輸出y及其導數可以得到:
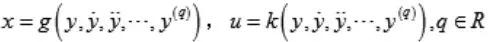
則該系統稱為微分平滑系統,并稱y為系統的平滑輸出。
有了上面的定義鋪墊,現在我們來探討UGV的微分平滑特性,其主要結論以下面的定理形式給出。
定理 UGV運動學模型式是微分平滑的,且平滑輸出可以表示為。
證明 由前述可知UGV系統的狀態變量為(x, y, θ),控制變量為(υ, ω)。由式,有:

從以上各式可以得知,系統所有狀態(x, y, θ)及控制輸入(υ, ω)均可由平滑輸出x、y及其導數的函數來表示,因此根據微分平滑系統的定義,定理成立。
上述定理表明UGV的運動控制系統在實施軌跡跟蹤控制時具有微分平滑特性,這可使其運動參考軌跡的選擇及相應軌跡的跟蹤控制律設計得以簡化,下面給出一種參考做法如下:選擇兩個充分光滑的函數和,其中考慮到UGV受到非完整性約束以及為了避免奇異值的出現,要求;再令這兩函數
3 軌跡跟蹤控制系統設計
為了方便后文的公式推導,將UGV運動學模型式進行轉換,有:

本文的軌跡跟蹤控制方案由內外嵌套的兩個控制子系統構成,位置跟蹤子系統為外環, 姿態鎮定子系統為內環;外環根據參考位置信號(xr, yr)生成一個中間指令信號作為參考角度信號θr,并傳遞給內環系統,內環則通過準滑模控制律實現對這個參考角度信號θr的跟蹤。控制系統的結構圖如圖2所示。

圖2 UGV的嵌套雙閉環的軌跡跟蹤控制器結構
3.1 位置控制律設計
下面設計外環的位置控制律υ,以實現輸出位置(x, y)跟蹤參考位置(xr, yr)。
令跟蹤誤差為:
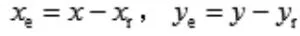
則有:

取滑模函數為:
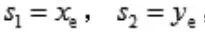
則有:
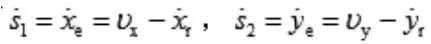

設計位置控制律為:其中,k1>0,k2>0,η1>0,η2>0,sat(●)是飽和函數。
采用文獻[4]的結論,上述不等式方程的解分別為:

從而Vx、Vy分別指數收斂于零,從而s1、s2分別指數收斂于零,從而xe、ye分別指數收斂于零,這樣我們通過設計的位置控制律υx和υy實現了x跟蹤xr,以及y跟蹤yr。
最后,把位置控制律υx和υy代入式,我們得到實際的位置控制律為:

3.2 姿態控制律設計
下面來設計內環的姿態控制律ω,以實現控制角度θ跟蹤位置子系統控制器生成的參考角度θr。
令θe=θ — θr,取滑模函數為s3=θe,則:
設計姿態控制律為:


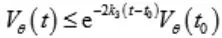
4 仿真實例

圖3 參考軌跡的跟蹤

圖4 參考位置及位置子系統控制器生成的參考角度的跟蹤
由上面的系列仿真圖可見,在設計的控制律作用下,UGV的實際軌跡漸進收斂于參考軌跡,UGV的實際位姿狀態亦快速收斂于參考位姿狀態。
結論
本文分析了欠驅動無人地面車輛的運動模型,證明了它是微分平滑系統并得到平滑輸出。基于微分平滑理論選取了欠驅動UGV的一個可行參考軌跡,然后推導了使該參考軌跡的跟蹤誤差漸近收斂的控制律。最后通過計算機仿真驗證了文中方法的有效性。
[1]施皖,毛麗民,俞雷,魯波.基于熱釋紅外的螞蟻搜索機器人群智系統設計[J].電子世界,2014(05):154-156.
[2]M.Fliess,J.Levine et al.Flatness and defect of non-linear systems:introductory theory and examples[J].International Journal of Control,2003,61(6):13-27.
[3]Kanayama Y et al.A stable tracking control method for an autonomous mobile robot[C].IEEE International Conference on Robotics and Automation,1990:384-389
[4]P.A.Ioannou,Jing Sun.Robust Adaptive Control[M].Prentice Hall PTR,1996.

