對稱照明在傅里葉疊層成像中的應用?

張雷雷 唐立金 張慕陽 梁艷梅

1)(南開大學現代光學研究所,光學信息技術科學教育部重點實驗室,天津 300350)2)(中國洛陽電子裝備試驗中心,光電測試與評估技術重點實驗室,洛陽 471003)

對稱照明在傅里葉疊層成像中的應用?

張雷雷1)2)唐立金1)張慕陽1)梁艷梅1)?

1)(南開大學現代光學研究所,光學信息技術科學教育部重點實驗室,天津 300350)2)(中國洛陽電子裝備試驗中心,光電測試與評估技術重點實驗室,洛陽 471003)

(2017年3月10日收到;2017年8月19日收到修改稿)

傅里葉疊層成像技術是一種全新的能夠恢復出大視場下高分辨率圖像的技術,而較長的采樣時間限制了傅里葉疊層成像的實際應用.本文闡述了一種利用對稱照明提高傅里葉疊層成像速度的方法,研究了傅里葉疊層成像在空域和頻域上的對稱性,指出在不考慮相位的情況下,利用對稱照明可提高照明強度,減少傅里葉疊層成像所需要的圖像數,同時可以提高傅里葉疊層成像圖像重建的速度.實驗表明使用對稱照明可以在不改變算法復雜性的前提下,得到與傳統傅里葉疊層成像同樣的高分辨率,且所需的圖像數減少約50%,采樣時間減少約70%,圖像重建時間減少約50%.基于對稱照明的方法將促進傅里葉疊層成像技術在實時成像中的應用.

對稱照明,傅里葉疊層成像,圖像重建

1 引 言

傅里葉疊層成像技術(Fourier ptychography,FP)是近幾年發展起來的一項全新的用于恢復樣品高分辨率強度和相位的技術[1?11].FP使用簡單的設備和簡練的算法,實現了樣品大視場條件下的高分辨成像,同時可進行三維重聚焦[12,13].FP系統將傳統顯微鏡中的照明系統替換為一個可編程控制的發光二極管(LED)陣列,依次點亮各LED產生不同方向的照明光,對樣品頻譜產生不同程度的遷移,并記錄在一系列低分辨圖像中.對這些低分辨圖,通過頻域和空域的迭代更新,重建出更豐富的樣品頻譜信息.最后,經逆傅里葉變換得到樣品的高分辨率強度圖和相位圖.FP解決了物鏡數值孔徑對分辨率的限制,使得低數值孔徑的物鏡也能得到高分辨率.

限制FP速度的主要因素是較多的低分辨圖像數量和較低的LED強度導致的電荷耦合器(CCD)較長的曝光時間[1].為了提高FP的速度,國內外學者進行了大量的研究.傳統FP需要對同一LED采集多個不同曝光時間的低分辨率圖像,然后進行高動態范圍合成,Dong等[14]將稀疏采樣引入FP,通過一個模板剔除低分辨率圖像中過曝光和過暗的像素,將傳統FP圖像數從多于445幅減少到225幅.Bian等[15]提出了基于內容的自適應照明方式,篩選出傅里葉頻譜中信息最豐富的區域對應的低分辨率圖像,利用FP重建高分辨率圖像,可以減少30%—60%的采樣時間.Zhang等[16]基于內容的自適應照明原理,提出了自學習FP技術,使用低分辨率圖像預測頻譜信息最豐富的區域,且僅點亮這些區域所對應的LED,可以減少約70%的低分辨率圖像.Guo等[17]研究了LED燈板布局對成像效果的影響,并設計了一種非均勻圓形LED照明器,與傳統LED陣列相比,可以減少50%的圖像數,且能獲得更好的恢復效果.這些方法都采用單個燈順序點亮的方式,仍然受限于LED的亮度.Dong等[18]提出光譜復用和相干態解析方法,通過同時點亮兩個相鄰的LED,然后對其頻譜進行解算,可以減少50%的圖像數.使用該原理同時點亮紅綠藍三色LED,可實現黑白相機采集并恢復出高分辨率彩色圖像.Tian等提出多路復用照明[19]和計算照明[20]同時隨機點亮4—8個LED,然后在迭代過程中將低分辨率圖像的強度和頻譜進行分解,恢復出高分辨率圖像,將FP所需圖像數減少到21幅,達到同樣的分辨率傳統FP需要173幅.上述多燈照明的方法減少了FP所需圖像的數目,但恢復過程中需要更多的時間.

經過幾年的發展,FP的成像速度得到了很大提高,但仍不能滿足實時采樣的需求.本文利用FP在空域和頻域的對稱性,提出了一種對稱照明FP(symmetry illumination Fourier ptychography,SFP),在不關注樣品相位的情況下,利用對稱照明,不僅能夠減少FP所需的圖像數量,而且能提高照明的亮度.該方法可以直接與其他提高FP速度的方法結合,不增加系統和算法的復雜性.

2 FP中的對稱性

2.1 空域對稱性

傅里葉疊層成像系統通常包含LED陣列、樣品、物鏡、筒鏡(tube lens)和相機五個部分.本文采用了195 mm共軛的物鏡構成的單筒顯微鏡,因此沒有筒鏡,系統原理圖如圖1所示.物鏡齊焦距離為45 mm,機械筒長為150 mm.LED陣列與樣品的距離遠大于系統的成像范圍,因此單個LED可以看作相干點光源.LED發出的近似平行光,照射樣品,經過物鏡的放大,利用相機采集不同角度照明下的樣品強度分布.

圖1 FP系統原理圖Fig.1.Schematic diagram of FPM.

假定LED陣列包含n個LED點源,中心燈的坐標為(n+1)/2.第i個LED對應的波矢為(kxi,kyi),其對樣品進行照明時,輸出的復振幅分布為

式中Ai(x,y)為第i個LED照明時系統的輸出復振幅分布,h(x,y)為系統相干點擴散函數,?表示卷積算子,Aobj(x,y)為樣品的復振幅分布,ej(kxix+kyiy)表示第i個LED的單位入射平面波.同理,第n?i+1個LED照明時,其輸出復振幅分布為

考慮到第i個LED與第n?i+1個LED存在中心對稱關系,則

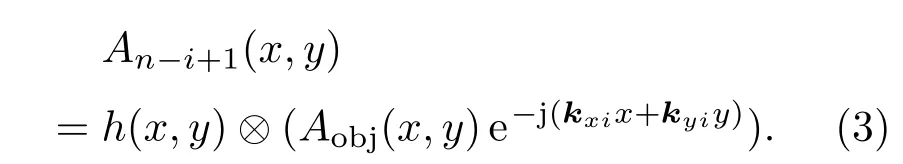
若忽略樣品的相位,則樣品Aobj(x,y)為一實函數,可以得到

式中,|Ai(x,y)|2=Ii(x,y),|An?i+1(x,y)|2=In?i+1(x,y)分別表示第i個LED和第n?i+1個LED照明時,系統輸出的光強.由于CCD只能記錄樣品的光強,而不能記錄相位,因此對稱位置的LED照明時,系統采集到的低分辨率圖像具有相同的強度分布.圖2給出了兩組對稱照明時的輸出強度的對比圖.其中圖2(a1)和(a2)為輸入圖像的強度和頻譜.圖2(b1)和(b2)以及圖2(c1)和(c2)為兩組對稱照明下的輸出圖像,分別對應于圖2(a2)中紅色和藍色的頻譜區域.

由于對稱位置的兩個燈不相干,因此同時點亮時,系統出射強度符合非相干疊加的原理,像的強度是單個LED照明時的兩倍.

式中,Ii(n?i+1)(x,y)表示第i個和第n?i+1個LED同時照明時系統輸出的強度分布.對于相位特征不明顯的薄生物樣品,用對稱照明能得到相近的強度分布.而且在FP實驗中,很容易實現光的對稱照明,因此在忽略樣品相位、僅考慮其強度分布時,可以通過同時點亮對稱的兩個燈來減少所需低分辨率圖像的數量,并提高照明的強度.

圖2 (網刊彩色)對稱照明下的強度對比圖 (a1)輸入圖像強度;(a2)輸入圖像頻譜;(b1),(b2)為圖(a2)中紅色虛線和實線區域對應的低分辨率圖;(c1),(c2)為圖(a2)中藍色虛線和實線區域對應的低分辨率圖Fig.2.(color online)Comparison of intensity images at symmetry illumination angle:(a1)Input intensity image:(a2)Fourier spectrum of input intensity image;(b1)and(b2)low-resolution images corresponding to the red regions in(a2);(c1)and(c2)low-resolution images corresponding to the blue regions in(a2).

2.2 頻域對稱性

空域對稱性可以用于減少所需圖像數,提高照明強度,對稱位置的照明在頻域也具有對稱性.將(1)式和(3)式變換到頻域,可以得到

式中Gi(kx,ky)和Gn?i+1(kx,ky)分別表示第i個和第n?i+1個LED照明時系統輸出的頻譜,H(kx,ky)為相干傳遞函數,Gobj為樣品的傅里葉頻譜.可以看出不同位置的LED照明對樣品的頻譜產生了一定頻移.

由于成像系統相當于一個低通濾波器,對于圓形光瞳,相干傳遞函數可以表示為

式中NA為物鏡的數值孔徑,k0=2π/λ為空間波矢.在不考慮樣品相位的情況下,Aobj(x,y)為一實函數,則其傅里葉變換Gobj具有中心共軛對稱性,H(kx,ky)為一實數濾波器,則Gi(kx,ky)和Gn?i+1(kx,ky)關于中心共軛對稱,那么兩者逆傅里葉變換的強度相等.利用頻譜的中心共軛對稱性,在FP恢復的過程中,可以僅恢復樣品一半的頻譜,另一半采用其共軛,這樣可以提高FP算法的重建速度.

3 實驗與討論

3.1 模擬實驗

利用對稱照明的原理,進行了模擬實驗,實驗參數如下:物鏡為4×0.1NA,像元尺寸為4.8μm,采用15×15的LED陣列,LED的中心波長為630 nm,相鄰LED的間距為5 mm,樣品與LED的距離為78 mm.采用圖像“Cameraman”作為輸入的樣品強度分布,圖像初始大小為(256×256)像素,通過插值擴大為(800×800)像素.

首先,考慮空域的對稱性.實驗中,模擬對稱的LED燈進行照明,將兩個LED照明時得到的低分辨率圖像的強度相加,然后利用FP算法進行重建.實驗結果如圖3所示.圖3(a)為輸入的樣品強度分布,作為真值;圖3(b)為采集到的低分辨率圖像;圖3(c)和圖3(d)分別給出了采用對稱照明和逐個LED照明條件下的FP恢復的樣品強度圖.

圖3 SFP和傳統FP的模擬實驗結果(a)輸入樣品強度圖;(b)低分辨率圖像;(c)SFP恢復的強度圖像;(d)傳統FP恢復的強度圖像Fig.3.Simulation experiment results of SFP and traditional FP:(a)Ground truth;(b)low resolution image;(c)recovered intensity image using SFP;(d)recovered intensity image using traditional FP.

圖4 SFP頻域對稱性模擬實驗結果(a)輸入圖像的頻譜;(b)SFP利用頻域中心共軛對稱性恢復的強度圖像;(c)SFP恢復出的一半頻譜;(d)SFP恢復出的全部頻譜Fig.4.Simulation experiment results of SFP using symmetry in Fourier domain:(a)Fourier spectrum of input intensity images;(b)recovered intensity image of SFP using conjugate symmetry in spectrum;(c)half of the recovered spectrum using SFP;(d)the recovered entire spectrum using SFP.

采用兩種方法恢復的圖像與輸入圖像的均方根誤差(RMSE)分別為0.0087和0.0088.模擬實驗結果表明,在不考慮相位的情況下,采用對稱照明可以達到與傳統FP相同的高分辨率恢復效果.

其次,考慮到頻域的中心共軛對稱性,在重建過程可以僅恢復樣品一半的頻譜,另一半頻譜采用其共軛,實驗結果如圖4所示.圖4(a)為輸入圖像的頻譜,圖4(b)給出了利用頻域中心共軛對稱性恢復的樣品圖像.圖4(c)為恢復出的一半頻譜.圖4(d)為圖4(c)中心共軛對稱得到的樣品的全部頻譜,其中虛線框所包含的區域為中心共軛對稱得到的樣品頻譜.從實驗結果可以看出,利用頻譜中心共軛對稱性,僅需要恢復一半的頻譜,就能得到樣品的強度分布,可以減少50%的計算時間.

3.2 SFP系統實驗

利用與模擬實驗相同的實驗參數,分別對USAF分辨率板和水螅切片進行了實驗.相機采用PointGray FL3-U3-13Y3 M-C黑白CMOS相機(1280像素×960像素),像元尺寸為4.8μm.物鏡為4×0.1NA195 mm共軛的平場物鏡(江南顯微鏡).采用一個可編程控制的32×32 LED陣列作為光源,實驗中僅點亮中心區域的15×15個LED.采用Arduino Mega 2560作為LED陣列的控制器.樣品與LED陣列距離為78 mm,最大照明NA為0.53.

利用上述系統,采用對稱照明時,采集到113幅低分辨率圖,傳統FP為225幅.利用FP重建算法,得到了樣品的高分辨率圖像,實驗結果如圖5所示.圖5(a1)為采用USAF分辨率板作為樣品時采集到的低分辨率圖像.圖5(a2)和(a3)分別為采用對稱照明和逐個LED照明時恢復的高分辨圖像.從圖中可以看出兩種方法恢復的結果均能分辨出分辨率板的線對9-3(645 lp/mm).

圖5(b1)給出了采用水螅切片作為樣品時的低分辨率圖,圖像像素數為200×200.圖5(b2)和(b3)分別為采用對稱照明和逐個LED照明時恢復的高分辨圖像,像素數為800×800.實驗結果表明,采用兩種方法均能恢復出樣品的高分辨率圖像,樣品的細節更加清晰,能夠分辨出低分辨率圖像中無法區分的單個細胞.

系統合成NA為0.63,理論分辨率為0.61μm,實際分辨率為0.775μm.實際分辨率小于理論分辨率是由于遠離中心的LED照明角度較大,對應的低分辨率圖中樣品的信號較弱,且在設置較長的曝光時間和較大的相機增益時,圖像的噪聲較大,圖像信噪比較低.

從兩種樣品的實驗結果可以看出,SFP得到了與FP同樣分辨率的結果,SFP恢復的圖像對比度略優于FP恢復的圖像.這是由于SFP具有更高的照明強度,因此可以設置更低的相機增益,圖像的噪聲比FP小.同時由于SFP忽略了樣品的相位,提高了頻域的對稱性,因此得到了比FP更高的對比度.

實驗結果表明,對于無相位的分辨率板以及相位信息不明顯的薄生物樣品,采用對稱照明時,在圖像數減少約50%時,得到了與傳統FP同樣的高分辨率強度圖.同時,由于對稱照明具有2倍的照明強度,實驗的總采樣時間縮短了約70%.

圖5 SFP和傳統FP的實驗結果(a1),(b1)低分辨率圖像;(a2),(b2)采用SFP恢復的高分辨率圖像;(a3),(b3)采用傳統FP恢復的高分辨率圖像Fig.5.Experiment results of SFP and traditional FP:(a1)and(b1)Low resolution images;(a2)and(b2)recovered intensity images using SFP;(a3)and(b3)recovered intensity images using traditional FP.

3.3 自適應的對稱照明

圖6 SFP和AFP的實驗結果(a),(b)采用AFP恢復的強度圖像和頻譜;(c),(d)SFP結合APF恢復出的強度圖像和頻譜Fig.6.Experiment results of SFP and AFP:(a)Recovered intensity image using AFP;(b)recovered spectrum using AFP;(c)recovered intensity image using SFP and AFP;(d)recovered spectrum using SFP and AFP.

對稱照明不改變系統的結構,也不增加算法的復雜度,可以直接與其他提高FP成像速度的方法結合使用,本文僅給出了SFP結合文獻[15]中基于內容的自適應照明方法(adaptive Fourier ptychography,AFP)提高FP速度的結果.AFP通過篩選低分辨率圖中信息最豐富的圖像,進行樣品高分辨率圖的恢復,從而減少FP所需的圖像數.圖6給出了SFP結合AFP恢復的高分辨率強度圖像和頻譜結果.逐個LED照明時,利用AFP方法篩選出了111幅圖像,恢復出樣品的強度圖和頻譜如圖6(a)和圖6(b)所示.使用SFP結合AFP時,僅需要56幅圖像恢復出了同樣分辨率的圖像,如圖6(c)和圖6(d)所示.

使用SFP結合AFP,使FP所需要的低分辨率圖像從225幅減少到56幅,且保證了恢復圖像的分辨率.實驗結果表明,SFP可以結合其他加快FP速度的方法,進一步提高FP成像速度.

4 結 論

本文利用FP在空域和頻域的對稱性,在不考慮相位信息的情況下,對稱位置照明具有相同的輸出強度分布,且對稱位置的頻譜具有中心共軛對稱性.采用對稱照明的方式,可以減少FP實驗約50%的低分辨圖像,且照明強度提高兩倍,系統總采樣時間減少約70%.利用頻域的中心共軛對稱性原理,可以縮短約50%的計算時間.同時,本文的方法可以與其他提高FP采樣速度的方法直接結合使用,有利于FP實現高速采樣.

[1]Zheng G A,Horstmeyer R,Yang C H 2013Nat.Photon.7 739

[2]Ou X Z,Horstmeyer R,Yang C H,Zheng G A 2013Opt.Lett.38 4845

[3]Bian Z C,Dong S Y,Zheng G A 2013Opt.Express21 32400

[4]Zheng G A 2014IEEE Photon.J.6 0701207

[5]Dong S Y,Nanda P,Guo K K,Liao J,Zheng G A 2015Photon.Res.3 19

[6]Ou X Z,Horstmeyer R,Zheng G A,Yang C H 2015Opt.Express23 3472

[7]Xie Z L,Ma H T,Qi B,Ren G,Tan Y F,He B,Zeng H L,Jiang C 2015Chin.Phys.Lett.32 124203

[8]Xie Z L,Qi B,Ma H T,Ren G,Tan Y F,He B,Zeng H L,Jiang C 2016Chin.Phys.Lett.33 44206

[9]Sun J S,Chen Q,Zhang Y Z,Zuo C 2016Biomed.Opt.Express7 1336

[10]Pacheco S,Zheng G A,Liang R G 2016J.Biomed.Opt.21 026010

[11]Zheng G A 2016Fourier Ptychographic Imaging:a MATLAB Tutorial(San Rafael:Morganamp;Claypool Publishers)pp(1-1)–(5-4)

[12]Dong S Y,Horstmeyer R,Shiradkar R,Guo K K,Ou X Z,Bian Z C,Xin H L,Zheng G A 2014Opt.Express22 13586

[13]Tian L,Waller L 2015Optica2 104

[14]Dong S Y,Bian Z C,Shiradkar R,Zheng G A 2014Opt.Express22 5455

[15]Bian L H,Suo J L,Situ G H,Zheng G A,Chen H,Dai Q H 2014Opt.Lett.39 6648

[16]Zhang Y B,Jiang W X,Tian L,Waller L,Dai Q H 2015Opt.Express23 18471

[17]Guo K K,Dong S Y,Nanda P,Zheng G A 2015Opt.Express23 6171

[18]Dong S Y,Shiradkar R,Nanda P,Zheng G A 2014Biomed.Opt.Express5 1757

[19]Tian L,Li X,Ramchandran K,Waller L 2014Opt.Express5 2376

[20]Tian L,Liu Z J,Yeh L H,Chen M,Zhong J S,Waller L 2015Optica2 904

PACS:42.30.–d,87.64.M–,42.30.WbDOI:10.7498/aps.66.224201

*Project supported by the National Natural Science Foundation of China(Grant No.11374167)and the State’s Key Project of Research and Development Plan,China(Grant No.2016YFC0101002).

?Corresponding author.E-mail:ymliang@nankai.edu.cn

Symmetric illumination in Fourier ptychography?

Zhang Lei-Lei1)2)Tang Li-Jin1)Zhang Mu-Yang1)Liang Yan-Mei1)?

1)(Institute of Modern Optics,Nankai University,Key Laboratory of Optical Information Science and Technology,Ministry of Education,Tianjin 300350,China)2)(Key Laboratory of Electro-Optical Countermeasures Test and Evaluation Technology,Luoyang Electronic Equipment Test Center of China,Luoyang 471003,China)

10 March 2017;revised manuscript

19 August 2017)

Fourier ptychography(FP)is a newly developed imaging technology,which can reconstruct high-resolution(HR)wide- field image from a series of low-resolution(LR)images.The limitation of FP is its long acquisition and reconstruction time due to the numerous LR images that are needed and the low illumination intensity of light-emitting diodes(LEDs)which lead to long exposure time of imaging sensors.Many researches have been done to speed up FP.The available speeding-up methods with single LED illumination are still constrained by low illumination intensity of LED.Although multi-illumination methods can improve illumination intensity,they are time-consuming during spectrum decomposition.In this paper,we demonstrate a new efficient method,termed symmetric Fourier ptychography(SFP).For thin samples irrespective of phases,two center-symmetric illuminations generate the same intensity distribution,so that two center-symmetric LEDs used in FP can be lit up simultaneously and the illumination intensity is doubled.Spectra have central conjugate symmetry in Fourier domain so that only half of spectra need recovering,then,the processing time can be reduced by about 50%.Simulations are conducted with the ‘Cameraman’image as input amplitude.The LR images are generated based on the FP simulation process and then the LR images generated by LEDs from two center-symmetrical positions are summed.Furthermore,HR images are recovered by using FP reconstruction algorithms.It is found that root-mean-square-error of SFP is almost the same as that of traditional FP,which indicates that the SFP can achieve the same performance as that of traditional FP.Then,central conjugate symmetry is adopted in Fourier domain,where only half of spectra are recovered and the other half of spectra are obtained from conjugate symmetry.It proves that HR images can be recovered based on central conjugate symmetry in Fourier domain and 50%of processing time is saved.For imaging experiments of USAF target and biological samples,two LEDs of central symmetry are lit up simultaneously,and 113 LR images are gathered in contrast with 225 ones of traditional FP.It is also found that SFP can achieve the same resolution as that of the traditional FP.In the meantime,SFP can reduce about 50%LR images and save about 70%acquisition time without increasing the complexity of FP system and algorithms.In addition,SFP can be combined with other methods to further speed up the speed of FP,and its feasibility is proven by the experimental results of combination with adaptive Fourier ptychography.All results in this paper indicate that the proposed method has the potential to improve the application of FP in real-time imaging.

symmetric illumination,Fourier ptychography,image reconstruction

10.7498/aps.66.224201

?國家自然科學基金 (批準號:11374167)和國家重點研發計劃“數字診療裝備研發”重點專項(批準號:2016YFC0101002)資助的課題.

?通信作者.E-mail:ymliang@nankai.edu.cn