基于磁化電流法的雙穩壓電懸臂梁磁力精確分析?

張雨陽 冷永剛 譚丹 劉進軍 范勝波

(天津大學機械工程學院,天津 300350)

基于磁化電流法的雙穩壓電懸臂梁磁力精確分析?

張雨陽 冷永剛?譚丹 劉進軍 范勝波

(天津大學機械工程學院,天津 300350)

(2017年3月22日收到;2017年8月21日收到修改稿)

雙穩壓電懸臂梁結構常常用于振動能量采集系統,其中的非線性磁力與系統勢函數和動力學方程的建立緊密相關,非線性磁力的正確分析和精確計算對系統振動響應和能量采集效果的準確預測至關重要.本文采用形狀函數分析方法,通過懸臂梁彎曲斜率的整體積分計算,得到了懸臂梁末端的運動軌跡及其末端磁鐵精確的位置與姿態,并由此根據磁化電流理論建立了雙穩壓電懸臂梁能量采集系統的磁力計算模型,給出了末端磁鐵受到的水平軸向磁力和豎直縱向磁力及其合磁力的變化規律.數值模擬發現,隨著末端磁鐵豎直縱向位移逐漸增大,磁鐵受到的水平軸向磁力和豎直縱向磁力都會依次由排斥力轉變為吸引力,從而導致磁力合力的方向會隨磁鐵位移發生跨越兩個象限的大幅度變化.實驗驗證表明,磁力計算結果與實驗測量結果符合良好,其精確度優于現有文獻方法的精度,因此本文的方法可以準確預測雙穩壓電懸臂梁振動過程的磁力變化規律.

振動能量采集,雙穩懸臂梁系統,磁力計算,磁化電流

1 引 言

目前,隨著低功耗微機電系統(micro-electromechanical system,MEMS)技術與現代無線通訊技術的迅猛發展,電子設備俞漸小型化、微型化,微型電子設備要求持續不間斷的供電問題成為微機電技術發展的一大瓶頸[1,2].為了克服傳統電池尺寸大、壽命短、需要定期更換等問題,人們希望得到一種能夠吸收周圍環境中能量的自供電裝置.由于環境中振動現象普遍存在,因此振動能量的采集成為一種可替代傳統電池和可自我維持的新型能源開發方式,受到國內外學者越來越廣泛的關注[3].

在振動能量采集方式中,壓電式振動能量采集較為普遍,其能量密度大,結構簡單,便于微型化,使其在與微機電系統技術結合中發揮了很大的優勢[4].對于線性壓電懸臂梁振動能量采集結構,系統存在共振頻帶過窄、能量輸出效率低等問題,因此將磁鐵力引入系統中構成非線性壓電懸臂梁振動能量采集系統,可有效提高振動能量采集系統的能量輸出效率和寬頻帶激勵的適應性[5?8].

雙穩態結構是非線性壓電梁振動能量采集系統中的常用結構,其系統中磁鐵間作用力的建模分析與精確計算是非線性雙穩振動能量采集研究中的一個難點,它關系到系統勢函數的建立與穩態的確定,以及磁鐵尺寸、間距和磁化強度等參數的選取,并對系統的輸出響應和能量采集效果有著較大的影響.目前雙穩壓電梁的磁力分析與計算主要是依據磁偶極子[9?11]或磁化電流[12]理論.磁偶極子法關于雙穩壓電梁的磁力分析與計算已在文獻[9]中進行了闡述,本文只討論磁化電流法在雙穩壓電梁中的磁力分析與計算.在已有的文獻中,雙穩壓電梁的磁化電流法磁力計算模型主要考慮懸臂梁豎直縱向磁力對系統的影響,即只考慮垂直于懸臂梁水平軸方向的磁力分力的影響,認為磁力的水平軸向分力對懸臂梁振動響應的影響不大,可忽略不計[3,13,14].磁力模型的這種簡化應用實際上忽略了梁振動過程中真實磁鐵力(合力)的大小和方向變化對系統的影響,且對于懸臂梁末端磁鐵位置變化規律的近似計算較為粗略,這種簡化方法對于實際磁力的分析計算和梁的振動響應以及能量的采集效果帶來怎樣的誤差目前還沒有一個統一的分析結果,特別是針對梁的大位移振動響應,常規的小幅度、小角度、小偏轉等近似分析方法是否適用有待進一步研究考證.

為了精確完整地分析雙穩壓電梁的非線性磁鐵力,本文以雙穩壓電梁振動能量采集系統為研究對象,首先針對壓電梁的不同振動位移尺度,研究磁鐵在磁場中的位置姿態,然后建立磁化電流法的磁力分析計算模型,分析磁鐵間的作用力,并給出磁力計算的精確方法,闡明誤差產生的原因,為準確得到雙穩壓電懸臂梁系統的振動響應和能量輸出提供可靠的非線性磁力計算方法.

2 雙穩態壓電懸臂梁振動能量采集系統

雙穩態壓電懸臂梁振動能量采集系統(以下簡稱雙穩壓電梁系統)的結構如圖1所示,系統由基座E、帶有末端磁鐵A的懸臂梁C和固定在基座上的外部磁鐵B組成,外部磁鐵B位于懸臂梁的水平軸線延長線上,懸臂梁根部上下兩面分別對稱黏貼有壓電片D.兩磁鐵材料及形狀尺寸相同且相互排斥,由于這種磁鐵排斥力的存在,可使懸臂梁在水平軸線的上下兩側位置保持穩定的平衡態,而在水平軸線位置保持非穩定的平衡態.當系統受到外界激勵時,基座帶動懸臂梁振動使懸臂梁上的壓電片發生形變,根據正壓電效應,壓電片將產生電能輸出,即實現機械振動能向電能的轉化[15,16].

圖1(a)結構一般可簡化為質量彈簧阻尼模型,如圖1(b)所示.根據牛頓第二定律與基爾霍夫第一定律可得到系統的動力學方程與采集電路方程[15,17]:

其中P(t)為外界激勵;Fx為兩磁鐵的磁力在豎直方向上的分力;x(t)為末端磁鐵的豎直位移;V(t)為壓電片輸出電壓;m,k,η及θ分別為壓電懸臂梁的等效質量、等效剛度、等效阻尼及壓電陶瓷(PZT)的機電耦合系數;Cp是電路電容;RL為電路電阻.

圖1 (網刊彩色)雙穩壓電懸臂梁振動能量采集系統(a)結構示意圖;(b)等效模型Fig.1.(color online)Bi-stable piezoelectric cantilever beam energy harvesting system:(a)Schematic diagram of structure;(b)equivalent model of energy harvesting systems.

從(1)和(2)式可以看出,磁鐵間的作用力對壓電懸臂梁能量采集系統的機電能量轉換起著關鍵性的作用,決定了系統的穩態形式.系統振動過程中,懸臂梁末端磁鐵位置的變化導致磁力的大小和方向也在不斷變化,準確分析計算這種動態變化的磁力,可為雙穩壓電梁的振動響應和能量采集提供可靠的理論指導和評估依據.

3 雙穩壓電梁磁化電流法的磁力分析

3.1 懸臂梁末端軌跡計算

為精確計算出雙穩壓電梁系統中的磁力,需先求得懸臂梁末端磁鐵的位置和姿態,即確定懸臂梁末端磁鐵的轉角和水平軸向位移.為此,以懸臂梁根部為原點建立如圖2所示坐標系,懸臂梁上任意點和末端位置分別表示為P(up,vp)和Q(u,v).

圖2 懸臂梁形狀函數與末端位置Fig.2.Diagram of the cantilever beam‘s shape function and end positions.

懸臂梁上任意一點的縱向位移與懸臂梁自由末端縱向位移的關系形如下[18]:

其中,s表示懸臂梁上的任意點P沿中性軸到固定端的距離,v(u)表示懸臂梁末端豎直縱向位移關于水平軸向位置的函數,ψ(s)稱作懸臂梁的形狀函數.因必須使懸臂梁上任意點P的位移滿足邊界條件s=0,vp=0,故取形狀函數為[19]

其中λ為常數,lb為懸臂梁長度.對于懸臂梁自由末端,需使形狀函數滿足v(u)=v(u)ψ(u),即ψ(s)=ψ(u)=1,故得

令懸臂梁上任意點P的斜度,即點P的切線與水平u軸的夾角,為?p,則不難理解sinφp=v′p或cosφp=1?(lp?up)′[20,21],其中變量右上角的角分符號“′”表示變量對s的導數,由此可得:

由(7)式進一步計算懸臂梁末端位移,可得

化簡得到多項式:

將(9)式中的正、余弦項泰勒近似展開,取前兩項并舍去高階無窮小項,求得懸臂梁末端水平軸向位移與豎直縱向位移的關系為

取懸臂梁長為lb=44 mm,可得懸臂梁末端位置變化軌跡如圖3所示.當任意點P位于懸臂梁末端時,令其切線與水平軸的夾角為φp=φ,如圖2所示.該夾角φ可由下式計算:

圖3 懸臂梁末端位置變化軌跡Fig.3.The trace of the cantilever beam’s end position.

3.2 磁化電流法基本原理

經典電磁理論認為,鐵磁性材料在磁場中被磁化后,材料內部存在體內分子磁化電流,材料表面存在表面分子磁化電流.由于磁鐵A和B都是被均勻磁化的永磁體,其內部是線性各向同性介質,因此其磁化強度M為常數,內部磁化電流密度為Jm=?×M=0[22],表面磁化電流面密度為[23]

其中n為表面法向矢量,符號表示單位矢量.

對于雙穩壓電梁系統,其磁力計算模型可以視為懸臂梁末端磁鐵A的磁化電流在由外部固定磁鐵B的磁化電流產生的磁場中所受的安培力.記雙穩壓電梁系統中的兩磁鐵A,B的水平間距為d,兩磁鐵的長lA和lB、寬wA和wB、高hA和hB的尺寸及磁極擺放如圖4所示.

圖4 磁鐵幾何尺寸及其間距示意圖Fig.4.Schematic diagram of geometric dimensions and interval between two magnets.

3.3 磁感應強度計算

由畢奧-薩伐爾定律知,電流在空間任意點產生的磁感應強度B可以表示為:

其中I=SKmB為等效電流,S表示磁化電流所在表面的面積,可由(12)式得L為積分路徑,即電流路徑,dl為磁化電流的微小線元,r為電流微元指向待求場點的向量,μ0為真空磁導率.

為了便于計算分析磁鐵B在空間各點產生的磁感應強度,以磁鐵B為原點建立坐標系,如圖5所示.其磁化強度方向指向y軸正方向,大小為MB.

在圖5建立的坐標系中,磁鐵B各個表面的法向單位矢量為[13]:

圖5 磁鐵B磁化電流示意圖Fig.5.Schematic diagram of external magnet B’s magnetizing currents.

因此可得圖5坐標系中任意一點P(x,y,z)在x,y,z三個方向的磁感應強度分別為:

其推導過程詳見附錄A.

3.4 磁斥力計算

根據3.1節求得的懸臂梁末端位置,可進一步求解末端磁鐵A各表面磁化電流在外部磁場坐標系中的位置坐標.取懸臂梁任意彎曲狀態如圖6所示,O點為懸臂梁固定端位置,A點與B點分別表示懸臂梁末端磁鐵與外部磁鐵的中心,A0點為懸臂梁水平不發生形變時其末端磁鐵的中心位置,C點表示懸臂梁末端磁鐵A任意位置在水平y軸上的投影.取坐標原點在磁鐵B的中心.

圖6 懸臂梁末端磁鐵A與外部磁鐵B相對位置Fig.6.The relative position of external magnet B and magnet A at the end of cantilever beam.

假設磁鐵A所在區域受到的磁場分布均勻一致,那么可將其表面磁化電流位置等效視為分布在各表面中心[13],如圖7所示,可得磁鐵A各表面磁化電流在坐標系中的位置

其中φ是懸臂梁末端切線與水平軸的夾角,也是磁鐵轉角,由(11)式確定,e為末端磁鐵A中心在y軸上的投影到坐標原點距離,其值為

由圖6和圖7不難看出,(20)式中的q即為懸臂梁自由末端水平軸向位移,結合3.1節懸臂梁末端位置計算(8)式可表示為

圖7 磁鐵A表面磁化電流在坐標系中的位置Fig.7.The positions of magnetizing currents on the surface of magnet A in the coordinate system.

由于系統中兩磁鐵相斥擺放,因此當懸臂梁處于水平中心軸位置時,磁鐵A的磁化強度方向與磁鐵B相反,同理,由于均勻磁化,磁鐵A內部磁化電流體密度為零,其各表面磁化電流面密度為磁鐵A表面磁化電流在外部磁鐵B產生的磁場中所受的安培力為[24]

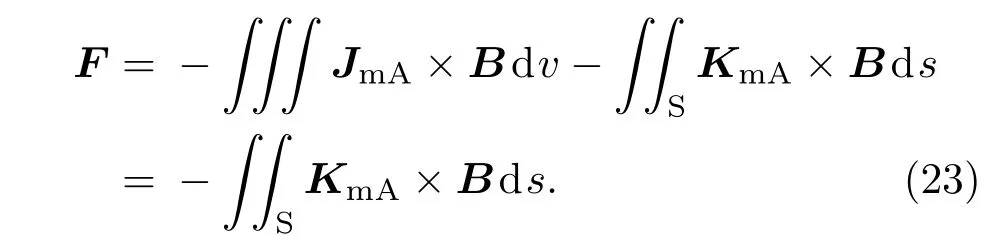
因此將(17),(18),(19)式和(22)式代入(23)式中可得:

其中S1=lAwA為磁鐵A上、下表面面積,S2=lAhA為磁鐵A前、后表面面積.

4 數值模擬

取磁鐵間距d=3 mm,其余參數見表1,對(24)式進行數值模擬,分別得到(豎直)縱向磁力Fi和(水平)軸向磁力Fj與懸臂梁末端磁鐵豎直縱向位移(即不同位置)的關系,如圖8所示.當懸臂梁末端磁鐵A離開水平y軸在x-y平面內沿圖3軌跡移動時,其所受到的軸向磁斥力會從最大值急劇減小而出現負值,表明懸臂梁末端磁鐵受到的軸向磁力由磁斥力變為磁引力,之后隨著縱向位移的增大逐漸趨近于零;對于磁鐵A受到的縱向磁力,隨著磁鐵縱向位移的增大,縱向磁力表現為磁斥力先增大然后減小,并且隨著縱向位移的繼續增大也變為負值,表明縱向磁力由磁斥力最終也變為磁引力.

受排斥力的末端磁鐵A隨豎直縱向位移的增大出現磁力變為吸引的現象,可用圖9磁感線走向變化加以解釋.兩磁鐵處于水平位置時,如圖9(a),其磁感線相互背離排斥.當末端磁鐵A偏離水平y軸較大位置時,由于懸臂梁的彎曲和磁鐵偏轉角度的存在,使得末端磁鐵A與外部磁鐵B的磁極指向及其磁感線走向變化成為如圖9(b)的形式,形成了表面磁感線相互接受吸引狀態,因此末端磁鐵A所受磁力會發生由磁斥力到磁吸引力的轉變.之前的研究中,對懸臂梁系統磁力的分析大都只局限在末端磁鐵的小范圍位移,很少考慮其磁力方向的改變.而實際應用中,當雙穩壓電懸臂梁振動達到較大位移時,磁引力的存在會減小系統勢函數的勢阱間寬度(即系統兩個平衡點的距離),進而使系統輸出位移響應變小并降低能量采集效果.

表1 雙穩能量采集系統參數Table 1.Parameters of bi-stable energy harvesting system.

圖8 懸臂梁末端磁鐵受到的縱向磁力和軸向磁力隨磁鐵位置的變化關系(d=3 mm)Fig.8.The lateral and axial magnetic force acted on the magnet at the end of cantilever beam varying with positions(d=3 mm).

圖9 系統磁感線走向 (a)磁鐵A處于水平位置;(b)磁鐵A處于大位移位置Fig.9.Schematic diagram of magnetic induction lines:(a)Magnet A at horizontal;(b)magnet A at a large displacement.

由(24)式可得末端磁鐵A受到的磁力合力大小為

其隨懸臂梁末端磁鐵縱向位移的變化如圖10所示,參數取值同上,其中Fx,Fy分別表示縱向磁力與軸向磁力的大小.磁力合力的方向與水平軸夾角為

圖10 (網刊彩色)懸臂梁末端磁鐵受到的縱向、軸向分力與合力大小隨位置的變化(d=3 mm)Fig.10.(color online)The lateral,axial and resultant magnetic force acted on the magnet at the end of cantilever beam varying with positions(d=3 mm).

為了進一步理解磁力合力的變化規律,以末端磁鐵A為中心建立極坐標系,其合力矢量F隨磁鐵位置變化如圖11所示,其中紅色曲線表示合力大小隨末端磁鐵縱向位移的變化,指向紅色曲線的黑色箭頭是任取若干位置合力的方向.可以看出,當懸臂梁末端磁鐵的位置由水平中心軸y逐漸向x軸正向遠離時,由于磁鐵間距變大,磁鐵力的大小隨之變小.而磁力的方向也經歷從第一象限到第二象限再到第三象限的變化(此處“象限”按角度劃分,與傳統直角坐標系定義不同,0?—90?為第一象限,依次類推).當水平軸向磁力與豎直縱向磁力都為磁斥力時,合力位于第一象限;當軸向磁力為吸引力,而縱向磁力為斥力時,合力在第二象限;隨著懸臂梁撓度和磁鐵偏轉角度增大,當縱向磁力和軸向磁力都為吸引力時,合力位于第三象限;隨后,隨著磁鐵位移繼續增大,合力于第三象限趨于零點.懸臂梁末端磁鐵向x軸負向遠離情況容易理解,這里不再贅述.

圖11 (網刊彩色)末端磁鐵的磁力合力隨豎直位移變化規律示意圖Fig.11.(color online)Schematic diagram of the resultant magnetic force acted on the magnet at the end of cantilever beam varying with vertical displacement in a polar coordinate system.

5 實驗分析

本文根據表1的參數制作了雙穩壓電懸臂梁能量采集系統,利用激光位移傳感器、測力計等測量設備搭建了磁力測量實驗系統,如圖12所示.懸臂梁采用錫鋼基體,在靠近根部位置貼有壓電片(PZT-5 A),懸臂梁自由端磁鐵A型號為N38 M,與之相同的另一塊磁鐵固定在推拉式測力計(HF-5)上,兩磁鐵同極相對擺放.改變外部磁鐵在測力計上的固定方式和裝配位置,可實現不同方向(軸向、縱向)力的大小的測量.調節末端磁鐵豎直方向的不同位置,其相應的位移和磁力大小可分別由激光位移傳感器(LK-G5001 V)和測力計測量讀出.

圖12 (網刊彩色)雙穩壓電懸臂梁磁力測量系統 (a)縱向磁力測量;(b)軸向磁力測量Fig.12.(color online)Bi-stable piezoelectric cantilever beam magnetic force measurement system:(a)Lateral magnetic force measurement system;(b)axial magnetic force measurement system.

5.1 實驗與模擬對比

依次由小到大任意選取幾個不等的磁鐵間距d:3,7,13,16,20 mm,實驗測量懸臂梁末端磁鐵不同豎直位移的磁鐵受力,并與模擬結果對比分析,如圖13所示,左圖為縱向磁力,右圖為軸向磁力,圖中圓圈點為實驗結果,實線為本文方法模擬結果,虛線為現有方法模擬結果.由于實驗中選用測力計零點漂移誤差為0.05 N,無法測量讀數小于0.05 N的磁力,因此圖中小于0.05 N的磁力只能用零值點表示.當磁鐵間距超過20 mm后,由于磁力均小于0.05 N,因此d=20 mm為“本實驗中”末端磁鐵能否受到磁力影響的臨界間距值,也是本實驗系統能夠測量到磁力的最大磁鐵間距.

從圖13磁力的實驗測量與模擬結果比較可以看出,除了小于0.05 N的磁力模擬曲線無法與實驗數據點匹配外,其余不同磁鐵間距和大于等于0.05 N的磁力模擬曲線幾乎都與實驗數據點匹配重合.

圖13(網刊彩色)不同磁鐵間距時磁力實驗值與本文方法、現有方法模擬值的對比 (a)d=3 mm;(b)d=7 mm;(c)d=13 mm;(d)d=16 mm;(e)d=20 mmFig.13.(color online)Comparison between experimental and simulation results from new and former calculation methods as di ff erent distances between two magnets:(a)d=3 mm;(b)d=7 mm;(c)d=13 mm;(d)d=16 mm;(e)d=20 mm.

5.2 與現有方法的比較

在現有文獻[13]的磁化電流法磁力分析研究中,3.1節中的懸臂梁末端偏角被近似為sin?≈x/lb,懸臂梁水平位移被簡化為lb?x≈lb(1?cosφ)[13],與本文(10)和(11)式的計算結果比較可知,其近似計算的偏角與實際中真實的偏角誤差較大,進而影響到水平位移計算的準確度,其模擬結果如圖13中虛線所示.而本文從懸臂梁形狀函數整體曲率考慮,通過積分累積可以更為精確地計算懸臂梁末端磁鐵的位置與姿態.為了定量分析本文方法的精度以及與現有方法比較,取實驗能夠測量到的且模擬值與實驗值誤差最大的點,如圖13(c)右圖軸向磁力最大偏離點,分別計算得到本文方法和現有方法的磁力的最大相對誤差為

顯然在最大誤差點處,本文方法與現有方法相比,最大相對誤差從38.66%減小到11.2%,表明本文磁力分析與計算方法的精確性和準確性有很大的提升.

從圖13還可以看出,現有方法對于懸臂梁在水平位置附近小幅度振動時,其磁力計算可以保持較高的精度,但是當振動激勵強度增大引起懸臂梁末端磁鐵產生較大位移以及較大磁鐵偏轉角度時,現有文獻中的磁力計算存在一定的誤差.因此磁鐵偏轉角度及其水平軸向位移的精確計算,對于懸臂梁振動過程磁力的準確預測估計有著重要的意義.

6 結 論

本文以雙穩壓電懸臂梁能量采集系統為研究對象,采用形狀函數分析方法,精確地給出了懸臂梁振動過程中其自由末端位置的軌跡及其末端磁鐵精確的位置與姿態,由此根據磁化電流理論揭示了豎直縱向磁力和水平軸向磁力以及磁力合力隨懸臂梁末端位置的變化規律.數值模擬發現,當懸臂梁自由末端磁鐵達到一定位移時,由于磁鐵存在較大的偏轉角度和水平軸向位移,導致磁力的正負性(排斥、吸引)會發生逆轉,從而末端磁鐵的磁力合力的方向會發生跨越兩個象限的大幅度變化,因此雙穩壓電懸臂梁能量采集系統的勢函數及其動力學特性會發生變化.磁力測量的實驗結果表明,磁力模擬曲線與實驗數據點高度匹配重合,證明本文給出的磁力分析與計算方法比已有的改進磁力計算方法具有更高的精度,可以有效預測估計雙穩壓電懸臂梁振動過程的磁力變化.

附錄A

正文中已提到畢奧-薩伐爾定律,簡稱“畢-薩定律”,其描述電流元在空間任意點P處所激發的磁場.用方程表示為

建立如圖A1中坐標系,如圖所示為一條沿z軸負向電流在任意點P處所產生的磁場,其中r為電流元dL到P點的向量,L為坐標原點到電流元dL的向量,I為電流大小,μ0為真空磁導率,B為P點的磁感應強度.圖中R表示坐標原點到P點的向量.

圖A1 電流產生磁場坐標系Fig.A1.Coordinate system of magnetic field produced by a current.

由圖A1可知:

且正文中已知表面電流面密度|KmB|=MB,因此得

將(A5)—(A7)式代入(A1)式中得:

正文圖5中,對于磁鐵B上、下、前、后表面電流激發的磁場,其分別表示為磁感應強度Bu,Bd,Bf和Bb,上下移動坐標系,通過坐標變換可得上、下表面電流產生的磁感應強度:

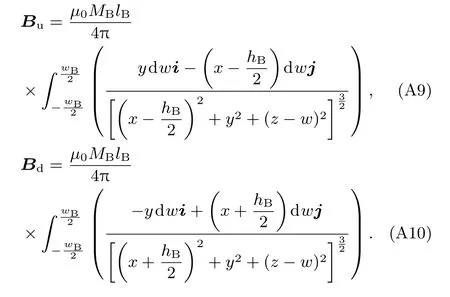
同理,可得前、后表面磁化電流產生的磁感應強度,其電流方向沿x軸,令L=hi,通過坐標變換得:

根據(A9)—(A12)式得Bi(x,y,z),Bj(x,y,z),Bk(x,y,z).

[1]Roundy S J 2003Ph.D.Dissertation(Berkeley:University of California,Berkeley)

[2]Sun J,Li Y G,Liu J Q,Yang C S,He D N 2009Micronanoelectr.Technol.46 673(in Chinese)[孫健,李以貴,劉景全,楊春生,何丹農2009微納電子技術46 673]

[3]Gao Y J,Leng Y G,Fan S B,Lai Z H 2014Smart Mater.Struct.23 095003

[4]Wang Q,Luo Y,Gu J Z 2008Electr.Compon.Mater.27 47(in Chinese)[王強,駱英,顧建祖 2008電子元件與材料27 47]

[5]Cottone F,Vocca H,Gammaitoni L 2009Phys.Rev.Lett.102 080601

[6]Andò B,Baglio S,Trigona C,Dumas N,Latorre L,Nouet P 2010J.Micromech.Microeng.20 125020

[7]Stanton S C,McGehee C C,Mann B P 2010Physica D239 640

[8]Fan K Q,Xu C H,Wang W D,Fang Y 2014Chin.Phys.B23 084501

[9]Yung K W,Landecker P B,Villani D D 1998Magn.Electric.Separat.9 39

[10]Neubauer M,Twiefel J,Westermann H,Wallaschek J 2012Small-Scale Energy Harvesting(Rijeka:InTech)p303

[11]Tang L H,Yang Y W 2012Appl.Phys.Lett.101 094102

[12]Akoun G,Yonnet J P 1984IEEE Trans.Magn.20 1962

[13]Tan D,Leng Y G,Fan S B,Gao Y J 2015Acta Phys.Sin.64 060502(in Chinese)[譚丹,冷永剛,范勝波,高毓璣2015物理學報64 060502]

[14]Lin J T,Lee B,Alphenaar B 2010Smart Mater.Struct.19 126

[15]Chen Z S,Yang Y M 2011Acta Phys.Sin.60 074301(in Chinese)[陳仲生,楊擁民 2011物理學報 60 074301]

[16]Ferrari M,Baù M,Guizzetti M,Ferrari V 2011Sens.Actuators A172 287

[17]Zhou S,Cao J,Erturk A,J Lin 2013Appl.Phys.Lett.102 101301

[18]Friswell M I,Ali S F,Adhikari S,Lees A W,Bilgen O,Adhikari S,Litak G 2012J.Intell.Mater.Syst.Struct.23 1505

[19]Esmailzadeh E,Nakhaie-Jazar G 1998Int.J.Non-Linear Mech.33 567

[20]Ali S F,Padhi R 2009P.I.Mech.Eng.I-J.Sys.Contr.Eng.223 657

[21]Nayfeh A H,Pai P F 2007Linear and Nonlinear Structural Mechanics(Hoboken:Wiley)pp65–110

[22]Agashe J S,Arnold D P 2008J.Phys.D:Appl.Phys.41 1586

[23]Bobbio S,Del fino F,Girdinio P,Mol fino P 2000IEEE Trans.Magn.36 663

[24]Furlani E P,Reznik S,Kroll A 1995IEEE Trans.Magn.31 844

PACS:05.45.–a,05.40.–a,02.60.CbDOI:10.7498/aps.66.220502

*Project supported by the National Natural Science Foundation of China(Grant No.51675370)and Tianjin Research Program of Application Foundation and Advanced Technology,China(Grant No.15JCZDJC32200).

?Corresponding author.E-mail:leng_yg@tju.edu.cn

Accurate analysis of magnetic force of bi-stable cantilever vibration energy harvesting system with the theory of magnetizing current?

Zhang Yu-Yang Leng Yong-Gang?Tan Dan Liu Jin-Jun Fan Sheng-Bo

(School of Mechanical Engineering,Tianjin University,Tianjin 300350,China)

22 March 2017;revised manuscript

21 August 2017)

In the study of piezoelectric cantilever energy harvesting system,a bi-stable nonlinear cantilever with magnets added to the structure has a wider frequency band response and a higher energy output efficiency.Hence,the calculation accuracy of the magnetic force on which the potential function and dynamics of the system depend is essential to predicting the output response and energy harvesting e ff ect.In this work,we use a shape function to describe the relation between the de flections of an arbitrary point and the free-end point on the beam,and then calculate the trace and de flection angle of the beam’s free-end by integrating the entire slope of the cantilever beam.The magnetic force is consequently derived from the magnets’real-time relative positions and postures by using the magnetizing current method.With comprehensively considering the axial magnetic force and the lateral magnetic force,the simulation results demonstrate that when the displacement of the magnet at the end of the beam is large enough,the directions of axial and lateral magnetic force change from repulsive to attractive,which leads to a large veer of the resultant magnetic force across two quadrants.So,it means that a smaller interval between magnets may not cause a larger de flection of the beam,and the magnetic force existing as attractive force could diminish the well space of potential function(that is,the distance between two equilibrium positions of the system).The experimental data in this work are nicely consistent with the simulation results.And in this work,we also make a comparison of the simulation results with those from our method and existing method,showing that the accuracy of the proposed method is much higher than that from the existing calculation method,especially in the scenario where the magnet at the end of the beam is far from the horizontal axis.

vibration energy harvesting,bi-stable cantilever system,calculation of magnetic force,magnetizing current

10.7498/aps.66.220502

?國家自然科學基金(批準號:51675370)和天津市應用基礎與前沿技術研究計劃(批準號:15JCZDJC32200)資助的課題.

?通信作者.E-mail:leng_yg@tju.edu.cn