拓撲聲子與聲子霍爾效應?

邢玉恒 徐錫方 張力發

(南京師范大學物理科學與技術學院,南京 210023)

拓撲聲子與聲子霍爾效應?

邢玉恒 徐錫方 張力發?

(南京師范大學物理科學與技術學院,南京 210023)

(2017年9月28日收到;2017年11月6日收到修改稿)

拓撲學與物理的結合是近幾十年物理學蓬勃發展的一個新領域,它不僅活躍在量子場理論以及高能物理中,更廣泛地存在于凝聚態物理體系中,包括量子(反常、自旋)霍爾效應和拓撲絕緣體(超導體)等.聲子是凝聚態體系中熱輸運的主要載體;最近由于各種聲子器件的發現,聲子學得到了廣泛的關注.本文介紹了聲子的拓撲性質以及聲子的霍爾效應現象,分別評述了在破壞時間反演對稱、破壞空間反演對稱、以及同時破壞時間和空間反演對稱三種情況下所產生的聲子霍爾效應、聲子谷霍爾效應等相關物理研究進展.最后對拓撲學在其他聲學體系中的應用做了簡單介紹,并進一步討論了其未來的發展方向.

拓撲學,Berry相位,Berry曲率,聲子霍爾效應

1 引 言

拓撲學是近代發展起來的一個數學分支,主要研究幾何圖形或空間在連續改變形狀后還能保持不變的一些性質的學科.早在十七世紀科學家就提出了“位置幾何學”和“相位分析”學說.1984年,英國布里斯托大學的科學家Michael Berry就提出了關于量子力學中的“幾何相”概念[1],主要描述了當一個量子體系在參數空間沿著閉合路徑緩慢變化時,系統本征態所發生的變化,即系統的哈密頓量在參數空間發生絕熱演化時體系的本征態的變化.Berry相在拓撲物理學領域是一個重要的概念[2],Berry曲率由于揭示了量子力學中絕熱過程的奧秘且最近因其在量子計算機的實現中的重要用途而引起了科學家們的廣泛興趣[3].Berry曲率最早出現在帶有布洛赫電子的單帶的動力學中,在應用于量子霍爾體系時,其半經典理論可以解釋霍爾電流和量子霍爾電導率[4].近幾年來,Berry相效應在解決鐵磁材料中的反常霍爾效應時起到了重要的作用[5,6],這也使Berry曲率在拓撲材料應用中的研究得到科學家們的廣泛關注.由于在拓撲物理方面原創性的貢獻,Thouless,Haldane和Kosterlitz被授予2016年諾貝爾物理學獎.拓撲和物理的巧妙結合,帶動了凝聚態物理的快速發展,比較有代表性的就是其近十年來逐漸興起的一個分支——拓撲絕緣體[7,8],即在絕緣體中帶隙中存在拓撲保護的邊界態.

由于熱二極管、熱晶體管、熱邏輯門等[9?11]的相繼提出,最近幾十年我們見證了聲子學的飛速發展,從而使得利用聲子進行熱流控制和信息處理成為可能.由于聲子作為一種中性的準粒子不能像電子一樣可以通過洛倫茲力直接和磁場耦合,因此當Rikken等[12]科學家在順磁介質樣品中發現聲子霍爾效應現象時,物理學家們普遍感到很驚奇,即在有熱流通過的樣品薄膜的垂直方向上施加磁場時可以觀察到橫向熱流,由于電子對熱流貢獻可以忽略,所以把這種現象稱之為聲子霍爾效應.此實驗被Inyushkin和Taldenkov[13]所重復.從那以后,科學家們提出了幾種理論來解釋這一現象[14].對于各種量子、自旋或反常霍爾效應的電子輸運性質,拓撲理論已經成功地解釋了一些潛在的機理,那么對于聲子的輸運性質是否也可以運用拓撲理論來進行研究呢？

2010年,Zhang等[15]將聲子的霍爾熱導率和聲子譜的Berry曲率聯系起來,揭示了聲子的拓撲性質，并發現了其中的拓撲相變,從而開創了拓撲聲子學的研究.其后,在2012年,Qin等[16]從能量磁化的角度對聲子霍爾熱導提出了修正.當磁場作用在具有自旋聲子相互作用的體系上時,時間反演對稱性會發生破缺,從而產生聲子霍爾效應.在非磁性體系中,空間反演對稱破缺而時間反演對稱性得到保護,可以觀察到谷聲子霍爾效應[17].在2016年,Zhang研究組又繼續通過半經典波包動力學方法統一研究了電子、聲子、磁子等熱霍爾效應,并得出了霍爾熱導率在拓撲理論框架下的通用公式[18].最近Liu等[19]研究了時間反演對稱性和空間反演對稱性同時破缺的體系中的拓撲聲子輸運現象.

本文以Berry曲率為切入點,著重討論Berry相以及Berry曲率的基本理論與性質.通過研究在單獨破壞時間反演對稱、破壞空間反演對稱以及同時破壞時間反演對稱和空間反演對稱的聲子體系中Berry曲率的變化對聲子輸運的影響.在本文的第二部分介紹了Berry相的基本理論知識,了解Berry曲率與拓撲結構之間的關系;第三部分介紹了破壞時間反演對稱時所產生的聲子霍爾效應,研究其中的Berry曲率對拓撲結構性質的一些影響;第四部分介紹了破壞空間反演對稱后形成的聲子谷霍爾效應;第五部分主要介紹同時破壞時間和空間反演對稱時對拓撲結構的影響;第六部分簡單介紹了Berry相效應在其他聲學體系中的應用;第七部分對拓撲聲子學的應用做了簡單展望.

2 Berry相及拓撲結構

Berry相位由三個至關重要的部分構成,這三個關鍵的特性決定了其在拓撲學中的重要地位.第一,Berry相位是規范不變的,其本征波函數由線性齊次方程定義,這個性質使得Berry相位更加的物理化,早期的實驗研究也是通過這個性質進行的.第二,Berry相位具有獨特的幾何性質,Berry相可以表示為在閉合參數空間的線性積分,且與實際路徑的變化率無關,Berry曲率的這種獨特的性質使得其得到了廣泛的應用.第三,Berry相位與規范場論和微分幾何有著密切的聯系,這使得Berry相成為一種直觀且意義十分重大的物理概念,尤其在今天的霍爾效應以及拓撲物理學的研究中具有重要的意義[7].

2.1 絕熱循環演化

波函數的整體相位不會對物理觀測造成影響,然而量子態之間的相對相位與很多的物理現象有關系.1984年,英國布里斯托大學的科學家Michael Berry提出了關于量子力學中的“幾何相”概念,為了更好地詮釋這個相位的物理意義,以下對這個相位進行簡單的推導.

當物理系統沿著參數空間中任意閉合回路做絕熱演化,其非簡并本征態的變化除了一個額定的相位之外,必然回到其本身,該相位就稱為Berry相位.設體系的哈密頓量算符是一組參量的R(R1,R2,···,RD)函數:

而R隨著時間做周期性變化

R(t)的周期變化在參量空間定義了一條閉合曲線C,假設此時周期T足夠大,以致哈密頓算符隨時間的變化非常緩慢,從而使得這一過程被稱為絕熱演化過程,致使系統在每一瞬間都是靜止的.于是,對于某一瞬時t,瞬時定態薛定諤方程成立.在絕熱條件下,瞬時本征波函數的含時薛定諤方程為

乘以〈m(R(t))|化簡后得

考慮一般含時薛定諤方程

在絕熱近似條件下,將本征函數歸一化條件求導可得

所以絕熱近似下式含時薛定諤方程的解為

在引入R(t)的空間“矢勢”后,Berry相位可以寫成

其中Bm(R)=?R×Am(R)稱為參數空間的“磁場強度”.

從上式可以看到:第一,Berry相位γm是實量;第二,Berry相位是一個規范不變的量,即在物理上是一個可以觀測的量;第三,Berry相位不依賴于系統參數演化的快慢,只與演化的路徑有關;第四,對于一維的參數空間,Berry相位為零,但是對于高維的參數空間,Berry相位不為零;第五,Berry相位是不可積的,也就是說它不能寫成一個關于參數R的連續函數[20].故Berry相位僅與閉合回路或者閉合曲面的幾何性質有關,與參數隨時間的變化率無關,因此,Berry相位又稱為幾何相位.

2.2 Berry曲率

通過(8)式以及下面恒等式:

所以Berry曲率可以寫成本征態的求和[21]:

在這里,通常將A稱為Berry聯絡(Berry connection),將B稱為Berry曲率(Berry curvature).

在上述的公式推導過程中,最重要的就是絕熱假設,即參數變化的足夠緩慢從而使體系一直約束在某個能級上.也就是說此時的取值空間已經從整個完備的希爾伯特空間投影到某一個特定的能級上,這就是產生Berry相位的本質.

2.3 Berry曲率與對稱性的關系

上述已經寫出的Berry曲率的表達式

滿足時間反演對稱時

滿足空間反演對稱時

若同時滿足空間和時間反演對稱

2.4 布洛赫能帶中的Berry相位

以上介紹了用哈密頓算子描述通用體系Berry相位的基本概念,現在考慮它在晶體中的實現.我們知道,晶體的能帶結構為研究Berry相效應提供了一個天然的平臺.在孤立電子近似下,首先可以寫出單電子情況下的哈密頓量:

其中V(r+a)=V(r),a是布拉伐晶格的格矢,通過布洛赫定理,周期性的哈密頓量的本征態滿足以下條件:

這里n是能帶的數目,?q是晶體的動量,通過進一步變換可得

在這里,unq(r)=e?iq·rψnq(r) 是布洛赫函數的周期性部分,滿足嚴格的周期性邊界條件unq(r+a)=unq(r).Berry相位以及Berry曲率可以寫成:

3 聲子霍爾效應

3.1 霍爾效應的發現

霍爾效應是電磁效應的一種,這一現象是美國物理學家霍爾于1879年在研究金屬的導電機理時發現的:即當電流垂直于外磁場通過導體時,載流子發生偏轉,在垂直于電流和磁場的方向會產生一附加電場,從而在導體的兩端產生電勢差,這個電勢差也被稱為霍爾電勢差.

圖1 (a)聲子霍爾效應示意圖,熱流方向在磁場作用下發生偏轉[24];(b)在Tb3Ga5O12薄膜樣品測得的橫向溫差隨磁場大小和方向的變化關系[12]Fig.1.(a)Phonon Hall e ff ect:the direction of the heat flow is de flected by the magnetic field[24];(b)magnetotransverse temperature di ff erence in a nonoriented sample of Tb3Ga5O15for heat currents perpendicular(circles)and parallel to the field(squares)[12].

近些年來,半導體材料和低維物理學的發展推動了許多霍爾效應的發展.在電絕緣的晶體中,聲子是熱流的載體,由于聲子不能直接和磁場相互作用,所以通常認為不存在聲子霍爾效應.最近,Strohm等[12]在順磁介質Tb3Ga5O12薄膜樣品中發現了聲子霍爾效應現象,如圖1所示,即在有縱向溫度梯度的順磁絕緣體薄膜上,加上垂直于薄膜平面的磁場后,測得橫向溫度差.當磁場方向平行于縱向熱流時,橫向溫度差可以忽略,然而當磁場方向垂直于縱向熱流(縱向溫差為1 K)時,可以觀察到200μK的溫度差.由于電子不參與熱輸運,所以Strohm等將之命名為聲子霍爾效應.此后該實驗并被Inyushkin和Taldenkov[13]所重復.科學家們試圖提出幾種理論來解釋這一現象[14,22],但是相對復雜并且有相互矛盾之處.另外,文獻[23]利用非平衡態格林函數方法研究了具有自旋聲子相互作用的四終端的二維薄膜的聲子霍爾溫差,從另一角度解釋了聲子霍爾效應.Zhang等[15]的工作從拓撲特性的角度首次對對聲子霍爾效應進行了揭示,下面首先從聲子霍爾體系的哈密頓量講起.

3.2 哈密頓量以及二次量子化

在有磁場存在的情況下[14],離子晶體中晶格格點的動能可以寫成

所以,上式可以寫成

如果此時沿z方向施加強度為B的磁場,前提是只考慮二維情況下的運動(即只沿x和y方向),此時離子α的動能可以寫成:

之前的理論中,科學家們考慮到拉曼相互作用的影響,基于量子理論和基本對稱性的自旋-聲子相互作用[26?28],得到了HI=h.(u×p),這里h=gcM,M與磁場B成正比.如果磁場沿z方向的作用,此時自旋-聲子相互作用可以寫成所以整個晶格的哈密頓量可以寫成[29]

這和(25)式類似.然而此哈密頓量并不總是正定的,我們應該選用(25)式,其始終是正定的.

哈密頓量是關于u和p二次型方程,可以寫出線性運動方程:

上式并不是標準的本征值問題,重新定義一個新的向量x=(μ,ε)T.然后,通過布洛赫定理,(28)式可以寫成[15]:

I是單位矩陣.因此,上式的本征值問題可以寫成

在這里,由于該有效哈密頓量是非厄米的,需要計(算右本征矢量為xk和左本征矢量對于本征矢εk的歸一化條件即為

對于上式中的本征值問題,可知完備基包括負的分支等.從聲子霍爾效應的拓撲性質可知[15],聲子霍爾熱導率的公式可以寫成包括正負頻的所有分支的貢獻形式,為了簡化符號,對于所有的分支,定義含時算子變換為變換關系為故由以上可以得到[15]:

這里的f(ωk)為玻色-愛因斯坦分布方程.

在上述變化后,位移和動量運算符可以用二次量子化算符寫成[30]:

這里|ωk|=ωksign(σ).通過上述,系統的哈密頓量可以寫成

通過一系列變換后,哈密頓量最終可以化為[30]

系統的熱流可以寫為[30]

這里V是N個基本原胞的總體積.通過對上述式的求導并引入Berry聯絡得出最終的熱流公式:

通過格林-庫珀公式,可以計算得到霍爾熱導線性響應貢獻κKubo:

其中:

是σ帶到σ′帶的對Berry曲率的貢獻.另外我們還必須考慮能量磁化貢獻ME[16],總的霍爾熱導率可以寫為

最終可以得到聲子熱導率公式[16]

這里[16]

從上述公式中可以看出聲子的霍爾熱導率由其色散關系和Berry曲率所決定,這與量子霍爾電導有一定的類比性[4].

此外,通過半經典的波包動力學方法,可以研究熱霍爾效應,包括電子熱霍爾效應、磁振子霍爾效應以及聲子霍爾效應.在熱霍爾效應中,可以定義粒子磁矩為

故體系的能量和熱磁矩分別為

這里εn是布洛赫能帶的能量,μ是化學勢.類比于電子軌道磁化,熱軌道磁化MQ有兩個部分,一個來自于波包的自轉有關,記為;另一個是波包中心的運動的貢獻,將其表示為[18].

可以得到總的熱流為

此公式是電子霍爾熱導、磁振子霍爾熱導以及聲子霍爾熱導的通用公式.其中對于聲子可以進一步寫成:

其中n,d分別是原胞內的原子數和每一個原子的自由度.

3.3 聲子霍爾效應的拓撲性質

由于本證矢量的波矢依賴性,可以計算其Berry相效應.通過 Berry近似,首先設x(t)=, 并代入上式中. 由于 Berry相,所以Berry曲率可寫成

然后通過將第一布里淵區域上的Berry曲率整合得到相關的拓撲陳數:

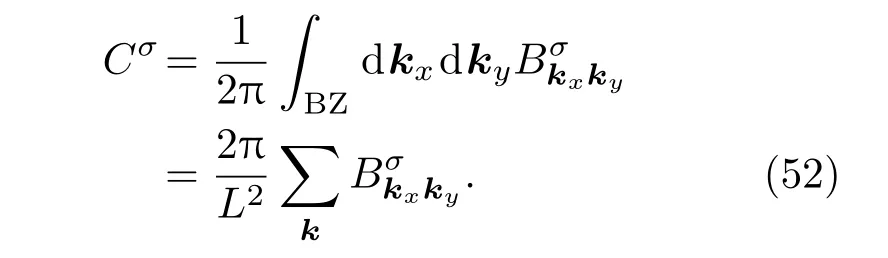
如果沒有拉曼自旋聲子的影響,也就是說當h=0時,此時 Berry曲率處處為零,聲子的霍爾熱導率消失.當外加磁場作用時,Berry曲率不為零,因此,聲子霍爾效應也隨之出現.另外研究發現,如果體系出現對稱性滿足SDS?1=D,SAS?1=?A,此時聲子的霍爾熱導為零[31],此時如果磁場改變了,Berry曲率也會改變,但是陳數在很大的范圍內并不改變.盡管陳數被量化了,但是由于(40)式中f(ωσ)(ωσ+ωσ′)2項的存在,聲子的霍爾熱導率并沒有被量化.

圖2 (a)—(d)當臨界磁場hc? =hc?10?2rad/ps時能帶1到4的Berry曲率輪廓圖;(e)—(h)當臨界磁場hc+=hc+10?2rad/ps時能帶1到4的Berry曲率輪廓圖;從(a)—(h)水平軸和垂直軸分別對應于波矢kx和ky;(i)在不同磁場中的Berry曲率,實線和虛線分別對應于在臨界磁場為hc?時?2和?3,相應的實點和虛點分別對應于臨界磁場為hc+時?2和?3;(j)四種能帶的陳數C1(實線),C2(虛線),C3(點線),C4(虛點線);(k)在臨界磁場為hc附近的不同磁場下能帶2和能帶3的色散關系圖,其中虛線、實線以及點線分別對應于在臨界磁場為hc?,hc,hc+時的帶[15]Fig.2.(a)–(d)The contour map of Berry curvatures for bands 1–4 at hc? =hc? 10?2rad/ps;(e)–(h)the contour map of Berry curvatures for bands 1–4 at hc+=hc+10?2rad/ps;for(a)–(h),the horizontal and vertical axes correspond to wave vector kxand ky;(i) ? at di ff erent magnetic fields,the solid and dashed lines correspond to ?2and ?3at hc?,respectively,while dotted and dash-dotted lines correspond to those at hc+;(j)Chern numbers of four bands,C1(solid line),C2(dashed line),C3(dotted line),and C4(dashdotted line);(k)the dispersion relation of bands 2 and 3 at di ff erent magnetic fields in the vicinity of hc,the dashed,solid and dotted lines correspond to the bands at hc?,hcand hc+,respectively[15].

隨著磁場的增加,在臨界磁場hc的附近,發現存在拓撲相變.不同頻帶在靠近臨界磁場的Berry曲率由圖2(a)—(f)給出,當hc附近磁場變化非常小時,在Γ點附近的能帶2和能帶3的Berry曲率幾乎是完全不同的,而能帶1和能帶4卻保持不變.如圖2(i)所示,在臨界磁場上方和下方Berry曲率發生了急劇的變化,從而導致能帶2和3的陳數發生跳躍,如圖2(j)所示,這個跳躍表明兩條帶的拓撲結構在臨界磁場下突然改變,這與能帶結構的相變有著重要的聯系[15].

為了進一步研究聲子拓撲帶結構變化的機理,同樣給出了在臨界磁場附近的聲子的色散關系圖,如圖2(k)所示,可以看到當磁場增加到hc時,在Γ點附近能帶2和能帶3彼此的相互靠近.同樣,在臨界磁場區域,兩條能帶發生了簡并且兩條帶的形狀出現了錐形.而在臨界點hc上方,兩條能帶發生了分裂.也就是說在臨界磁場附近的聲子的色散關系直接影響了Berry曲率,從而導致拓撲相變.

這里提出的聲子霍爾熱導率的拓撲學方法是一般的,可以應用于低溫下的真實材料.最近的研究發現它也可以用于磁霍爾效應[32].從拓撲性質和色散關系來解釋的聲子霍爾效應相變也可以推廣到研究其他霍爾效應或非平衡運輸中的相變.

4 聲子谷霍爾效應

4.1 谷電子霍爾效應

由于空間反演對稱性的破壞,動量空間里分開的不等價的能谷K,K′,通過Berry曲率或軌道磁矩可以來描述這種不等價性.因此這兩處不等價的能谷便構成了除電荷和自旋以外電子的另一個自由度,這也導致了能谷電子學的出現.

自然界大量存在類似于石墨烯的六角蜂窩狀晶格層狀材料,例如氮化硼、硒化鎵、過渡金屬二硫化物等.不同于石墨烯,這些材料中的A和B子格是由不同的原子構成,從而體系破壞了空間反演對稱性.這些材料也為研究能谷電子學提供了條件.

在A/B堆積的雙層石墨烯材料中,通過施加垂直與二維平面的電場來打破石墨烯的空間反演對稱性,從而在K和K′能谷處產生大小相等但反向的并且與能谷相關的Berry曲率及軌道磁矩[33].因此也帶來了一系列新奇的效應,如能谷霍爾效應[34].如圖3,在非零的Berry曲率和外加面內電場的作用下,谷電子獲得反常的大小與Berry曲率成正比[35,36]的橫向速度,不同的谷電子偏轉方向相反.因此在樣品兩端可探測到谷極化電流,圖中Berry曲率的反差使得K和K′能谷電子在垂直外加電場方向的運動發生橫向相反方向的偏轉,這就是谷電子霍爾效應.最近,實驗上已經在單層二硫化鉬三極管[37]和石墨烯超晶格[38]中觀測到了谷電子霍爾效應.

通過對稱性分析可知,破壞時間反演對稱性或破壞空間反演對稱性的系統中聲子攜帶非零的角動量.在這一部分,我們引入非磁性的六角AB晶格體系,即破壞空間反演對稱性,但保留時間反演對稱性.在兩個不等價的能谷處手性的聲子大量集中,即谷上的聲子是左旋或者右旋圓極化的,且非簡并的聲子模可以用量子的贗角動量標記[17].所以,類比谷電子霍爾效應,對于谷聲子,自然要提出兩個問題:谷聲子的Berry曲率是否為零？如果Berry曲率是非零的,是否存在谷聲子霍爾效應？

圖3 谷電子霍爾效應示意圖[34]Fig.3.Valley electronic Hall e ff ect diagram[34].

4.2 聲子Berry曲率

之前計算聲子的Berry曲率,采用傳統的晶格動力學周期解

這里的u和ε是維度為2(二維運動)或3(三維運動)的列向量.接著可以得到運動方程

而實際上,為了準確地得到聲子的Berry曲率,必須考慮到原胞內格點的相位差,因此這里采取布洛赫波形式的聲子波函數

其中dα是第α原子相較于第l個原胞的平衡位置,因此可以得出

所以動力學矩陣變為

此時的運動方程為

這與之前的運動方程是等價的,它們具有相同的色散關系,僅僅是波函數相差了一個相位.

在第二節已經計算過聲子的Berry曲率,這里由于具有時間反演對稱性,只需考慮所有正的聲子模.

由于ε(k,σ)=ε?(?k,?σ), 在時間反演對稱性的保護下, 有ε(k,σ)=ε?(?k,σ), 所以因此

類比于電子的Berry曲率計算Hψn=Enψn,聲子的Berry曲率為

這一形式也與第二節所給的聲子Berry曲率相符合.

4.3 谷聲子霍爾效應

非磁性的六角A/B晶格體系破壞了空間反演對稱性,如圖4(a),在能谷處觀察到了非零的聲子Berry曲率.能帶1和能帶4在能谷處擁有較大的Berry曲率,而能帶2和能帶3在能谷處的Berry曲率較小.正因為能谷處存在非零的Berry曲率,施加縱向的應變梯度Estrain,類比于谷電子霍爾效應,會出現與應變梯度和Berry曲率的叉矢成正比的反常速度,νanom∝?Estrain×B.因此,被左旋或者右旋極化光子激發的位于不同能谷處的聲子會沿橫向移動.如圖4(b)和圖4(c),如果光子的極性反轉,那么橫向聲子流的方向也會翻轉.隨著聲子在某條邊的積累,可以測得橫向的溫度差.很顯然,如果圓極化的受激光子極性反轉,則橫向溫差也會相反.

圖4 六角A/B晶格的聲子貝里曲率和谷聲子霍爾效應 (a)能帶1(底部二維圖)和能帶2(頂部三維圖)的Berry曲率;(b),(c)谷聲子被右旋或左旋極化光激發(霍爾熱流由紅色箭頭標出),在應力梯度下產生相應的聲子[17]Fig.4.Phonon Berry curvature and valleyphonon Hall e ff ect in a honeycomb of A/B lattice:(a)Berry curvatureof band 1(bottom contour plot)and band 2(top 3D plot);(b),(c)schematic of the valley phonon hall e ff ect(the Hall current denoted by the olive curve arrows)undera strain gradient(the orange arrows),where valley phononsare excited by a ray of right-handed or left-handed polarizedlight(the red wave lines)[17].

聲子霍爾效應已在實驗上證實[39],在順磁絕緣體中,磁場可以改變聲子的輸運,因此可以測得橫向的溫度差,但是其效應受限于及其微弱的自旋聲子相互作用.在破壞空間反演對稱性而保持時間反演對稱性的體系中,非零的Berry曲率誘發的谷聲子霍爾效應確實廣泛存在于六角晶格中,將會有更大范圍的應用.

5 同時破壞時間和空間反演對稱的聲子模型

由于時間反演對稱破缺會產生具有非零拓撲陳數的聲子態,即聲子霍爾效應,其具有單向導通的不受散射的聲子邊界模式;空間反演對稱破缺會產生具有非零的Berry相的谷,可用作調控聲子輸運的新型量子自由度,即谷聲子霍爾效應;如果兩種對稱性破缺同時存在,則能產生新的拓撲相變并演生出豐富的聲子拓撲量子態.

圖5 (a)由A/B晶格組成的蜂窩狀晶格示意圖,以及在K和K′聲子谷附近的狄拉克錐;(b)當同時破壞掉時間反演和空間反演對稱兩個谷的頻率不變,其中A/B晶格聲子態A由紅色標出,B由藍色標出[19]Fig.5.(a)A honeycomb lattice composed of A/B sublattices,and the Dirac cones of phonons near the K and K′valleys;(b)the two valleys that arenondegenerate in frequency caused by breaking P and T simultaneously[19].

Liu等[19]的最新研究中,利用類似于Haldane蜂窩晶格模型,研究并探索Berry相與聲子的拓撲效應.在這種晶格中,縱向光學和聲學模式在K處形成線性交叉條帶和 Dirac點,如圖5所示.當破壞空間反演對稱性以及時間反演對稱時,哈密頓量可以寫成:

在上述的介紹中,我們已經了解了單獨破壞時間反演對稱或者空間反演對稱對Berry曲率的影響,此時Berry通量在每個谷中的值為±π,且陳數CK(K′)=±1/2. 由于C=CK+CK′,故在單獨破壞時間反演時,Berry曲率B(k)=B(?k),陳數為C=±1,此系統中可以觀測到聲子霍爾效應;在單獨破壞空間反演對稱時,B(k)=?B(?k),陳數C=0,可以觀測到谷聲子霍爾效應.如圖5所示,當同時破壞時間反演和空間對稱性時,兩聲子谷之間的頻率簡并消失,K和K′之間的能帶帶隙打開且相互獨立,即在極端情況下,只能在一個谷中實現零帶隙能帶,這種發現可以應用在聲子谷濾波器中.

6 Berry相效應在其他聲學體系中的應用

近幾年,關于Berry曲率在聲學體系中的應用的研究很多,例如在低溫的情況下,磁絕緣體中的自旋激發的熱導率可超過聲子的自發激發的熱導率,但由于其電荷為中性的,故自旋波不會產生相應的熱霍爾效應.然而,在戈薇晶格,Berry曲率與熱導率之間有著緊密的聯系,在實驗中觀察到κ隨著溫度或磁場的變化而發生符號反轉,其與金屬帶之間的陳數通量的符號交替相關[40].其次,在電子和聲子相互作用的系統中,量子霍爾效應與無耗散電流情況下霍爾電導率之間也有著緊密的聯系,最近已經觀察到,當電流增加到一個臨界值時,對應于聲速的載波漂移速度出現了一個戲劇性的耗散[41].在反轉對稱性破壞的非磁性系統中,Berry曲率誘導橫向谷聲子霍爾效應將產生一些新的應用.

對于谷贗自旋,由于其作為新型信息載體的潛力巨大且在動量空間中能標注能量極值的量子狀態而引起了人們的關注[37,38,42,43].在最近的一項研究中,武漢大學劉正猷研究組從實驗上在聲波晶體中觀察到了聲音的拓撲谷輸運現象[44],他們除了通過聲場的空間掃描直接觀察谷選擇性邊緣模式之外,還在急劇彎曲的界面中觀察到抗反射現象.與傳統聲波導相比,拓撲保護的聲音傳輸與其明顯不同,這一發現可以作為設計具有非常規功能設備的基礎.

另外,近期劉正猷教授研究組在聲子晶體中首次引入谷自由度的概念,預測了聲學谷態所具有的渦旋聲場分布并提出了產生特定手性聲渦旋場的方法,在此基礎上,他們進一步實現了谷束分離和基于谷態的粒子操控.可以預期其潛在的應用與聲學渦旋及物質的異乎尋常的相互作用,例如觸發俘獲的微粒的旋轉而不接觸.這一發現具有重要的科學意義[45].

此外,通過剛性鍵或者彈簧連接起來的質點組成的框架或格子模型構造在結構工程、建筑和材料科學等不同領域有著重要的應用.在這類晶格中,剛性鍵的數量與格子自由度之間的差異決定了它們的“零頻率”軟盤模式的數量.當這些平衡時,系統處于機械不穩定的邊緣,被稱為等靜壓.由于某些擴展的等靜壓晶格在其邊界的軟盤模式呈現局部化,這些邊界模式對局部擾動不敏感,似乎具有拓撲起源,可聯想到在量子霍爾效應和拓撲絕緣子中發生的受保護的電子邊界模式.由此科學家們建立了拓撲機械模式和電子系統的拓撲帶理論之間的聯系,并預測了具有不同邊界模式的新的拓撲大體積機械相的存在[46].

最近,科學家在機械拓撲絕緣子中觀察到聲子的螺旋邊緣態,這一發現使得利用表面聲子的穩定性設計可靠的波導的拓撲聲學材料成為可能[47].在具有單向彈性邊緣波的拓撲聲子晶體中,科學家們通過使用陀螺慣性效應來打破時間反演對稱,實現電子量子(反常)霍爾效應的聲子模擬,研究結果激發了新型表面波器件的設計熱潮,將廣泛應用于電子、電信和聲學成像[48].

7 展 望

拓撲物理學是一個方興未艾的領域,有著很廣泛的前景等待著科學家們去開發.自從量子霍爾效應發現以來,凝聚態物理中的拓撲現象層出不窮,如拓撲絕緣體、拓撲超導體等.拓撲與聲子學的結合才剛剛開始,已有的相關研究工作中已可看到很大的發展空間和廣闊的應用前景.

在磁性體系中,聲子霍爾效應的發現給聲子輸運與控制提供了新的方法,但至今沒有更多的實驗研究聲子霍爾效應.由于絕大部分順磁材料自旋聲子相互作用很小,所以測得霍爾效應很弱,如何尋找更大效應的順磁材料是一個挑戰.另外鐵磁絕緣體,由于更大的磁化率和更大的自旋聲子相互作用,可以存在更強的的聲子霍爾效應,但是由于其中的磁振子霍爾效應也很強,所以區分鐵磁絕緣材料中熱霍爾效應中磁振子和聲子的貢獻也是一個很有意義的課題,由于磁振子和聲子的拓撲性質不一樣,拓撲聲子學在鐵磁材料中聲子霍爾效應可以發揮更大的作用.

塊體能譜的拓撲特性實際上也對應著非平凡的邊界態,那么對于這里的聲子霍爾效應,理論上應該存在相應的拓撲保護的邊界態或者邊界模式,和磁振子一樣聲子等玻色子體系中都沒有費米面的概念,所以真正意義上的玻色子拓撲絕緣體不存在,但是可以通過波導選擇帶隙中的模式,這樣磁振子和聲子拓撲絕緣體也可以存在.拓撲磁振子絕緣體已經發現,但是拓撲聲子絕緣體還沒有真正發現,尋找拓撲保護的邊界聲子模對于無耗散的聲子輸運控制及相關能量科學將具有潛在的應用價值.

谷聲子霍爾效應為聲子的控制提供了一個新的自由度.由于電子的谷間散射與谷聲子緊密聯系,如最近發現的谷聲子具有確定的手性并且決定電子谷間散射的選擇定則[16],因而谷聲子對谷電子學的發展意義重大.對于谷聲子相關理論,以及不同模型和材料中的手性聲子計算還需廣泛深入的研究.另外實驗直接觀測谷聲子以及谷聲子霍爾效應也是一項具有重大意義的研究.

對于同時破壞時空對稱性的體系,谷聲子的能量簡并打開,為實現單谷聲子的選擇與應用提供了思路.而如何找到這樣的材料還有待進一步的探索研究.

拓撲聲子學才剛剛開始.而拓撲與自旋電子學的結合已經引領了凝聚態物理幾十年.我們相信,由于聲子在凝聚態物理中廣泛存在,如超導、電聲相互作用、布里淵區及拉曼散射、熱電效應、熱效應等,拓撲聲子在這些領域中不可回避并起到關鍵作用,也將引領凝聚態物理學的蓬勃發展.

[1]Berry M V 1984Math.Phys.Sci.392 45

[2]Wilczek F,Shapere A 1989Geometric Phases Phys.5 05857

[3]Prabhakar S,Melnik R,Bonilla L L 2014Phys.Rev.B89 245310

[4]Thouless D J,Kohmoto M,Nightingale M P,den Nijs M 1982Phys.Rev.Lett.49 405

[5]Karplus R,Luttinger J M 1954Phys.Rev.95 1154

[6]Zeng C,Yao Y,Niu Q,Weitering H H 2006Phys.Rev.Lett.96 037204

[7]Hasan M Z,Kane C L 2010Rev.Mod.Phys.82 3045

[8]Qi X L,Zhang S C 2011Rev.Mod.Phys.83 1057

[9]Li B,Wang L,Casati G 2004Phys.Rev.Lett.93 184301

[10]Chang C W,Okawa D,Majumdar A,Zettl A 2006Science314 1121

[11]Li B,Wang L,Casati G 2006Appl.Phys.Lett.88 143501

[12]Rikken G L J A,Strohm C,Wyder P 2002Phys.Rev.Lett.89 133005

[13]Inyushkin A V,Taldenkov A N 2007JETP Lett.86 379

[14]Sheng L,Sheng D N,Ting C S 2006Phys.Rev.Lett.96 155901

[15]Zhang L,Ren J,Wang J S,Li B W 2010Phys.Rev.Lett.105 225901

[16]Qin T,Zhou J,Shi J 2012Phys.Rev.B86 104305

[17]Zhang L,Niu Q 2015Phys.Rev.Lett.115 115502

[18]Zhang L 2016New J.Phys.18 103039

[19]Liu Y,Xu Y,Duan W 2017 arXiv preprint arXiv:1707.07142

[20]Zhou J H 2012Ph.D.Dissertation(Beijing:Institute of Theoretical Physics,Chinese Academy of Sciences)(in Chinese)[周建輝 2012博士學位論文 (北京:中國科學院理論物理研究所)]

[21]Nagaosa N,Sinova J,Onoda S,MacDonald A H,Ong N P 2010Rev.Modern Phys.82 1539

[22]Kagan Y,Maksimov L A 2008Phys.Rev.Lett.100 145902

[23]Wang J S,Zhang L 2009Phys.Rev.B80 012301

[24]Zhang L 2011Ph.D.Dissertation(Singapore:National University of Singapore)

[25]Holz A 1972Nuovo Cimento B9 83

[26]Strohm C,Rikken G,Wyder P 2005Phys.Rev.Lett.95 155901

[27]Kronig R L 1939Physica6 33

[28]van Vleck J H 1940Phys.Rev.57 426

[29]Wang L and Li B 2007Phys.Rev.Lett.99 177208

[30]Zhang L,Ren J,Wang J S,Li B W 2011J.Phys.Condens.Matter23 305402

[31]Zhang L,Wang J S,Li B 2009New J.Phys.11 113038

[32]Onose Y,Ideue T,Katsura H,Shiomi Y,Nagaosa N,Tokura Y 2010Science329 297

[33]Xiao D,Yao W,Niu Q 2007Phys.Rev.Lett.99 236809

[34]Zeng H L,Cui X D 2016Acta Phys.Sin.45 505

[35]Chang M C,Niu Q 1996Phys.Rev.B53 7010

[36]Xiao D,Chang M C,Niu Q 2010Rev.Mod.Phys.82 1959

[37]Mak K F,McGill K L,Park J,McEuen P L 2014Science344 1489

[38]Gorbachev R V,Song S J C,Yu G L,Kretinin A V,Withers F,Cao Y,Mishchenko A,Grigorieva I V,Novoselov K S,Levitov L S,Geim A K 2014Science346 448

[39]Cao T,Wang G,Han W P,Ye H Q,Zhu C R,Shi J R,Niu Q,Tan P H,Wang E,Liu B L,Feng J 2012Nat.Commun.3 887

[40]Hirschberger M,Chisnell R,Young S,Lee N P 2015Phys.Rev.Lett.115 106603

[41]Heinonen O,Taylor P L,Girvin S M 1984Phys.Rev.B30 3016

[42]Xu X D,Yao W,Xiao D,Heinz T F 2014Nature Phys.10 343

[43]Rycerz A,Tworzydlo J,Beenakker C W J 2007Europhys.Lett.79 57003

[44]Lu J Y,Qiu C Y,Ye L P,Fan X Y,Ke M Z,Zhang F,Liu Z Y 2016Nature Phys.13 369

[45]Lu J Y,Qiu C Y,Ke M Z,Liu Z Y 2016Phys.Rev.Lett.116 093901

[46]KaneC L,LubenskyT C 2013arXivpreprint arXiv:1308.0554

[47]Süsstrunk R,Huber S D 2015Science349 47

[48]Wang P,Lu L,Bertoldi K 2015Phys.Rev.Lett.115 104302

PACS:66.70.–f,03.65.Vf,72.10.Bg,72.15.GdDOI:10.7498/aps.66.226601

*Project supported by the National Natural Science Foundation of China(Grant No.11574154).

?Corresponding author.E-mail:phyzlf@njnu.edu.cn

Topological phonons and phonon Hall e ff ects?

Xing Yu-Heng Xu Xi-Fang Zhang Li-Fa?

(School of Physics and Technology,Nanjing Normal University,Nanjing 210023,China)

28 September 2017;revised manuscript

6 November 2017)

The combination of topology and physics is a new field of physics development in recent decades.It is not only active in quantum field theory and high energy physics,but also widely exists in condensed matter physics,including quantum(anomalous,spin)Hall e ff ect and topological insulators(superconductors)etc.Phonon,as the main carrier of heat transport in the crystal,recently,due to the discovery of various phonon devices,phonons has been widely concerned by scientist.In this paper,we introduce the topological properties of phonons and the phonon hall e ff ect.We have reviewed the related physical research progress of phonon hall e ff ect,phonon valley hall e ff ect and so on,which are generated by breaking the time reversal symmetry,spatial inversion symmetry,both breaking the time and spatial inversion symmetry.Finally,the application of topology in other acoustic systems is brie fly introduced,and the future development direction is discussed too.

topology,Berry phase,Berry curvature,phonon Hall e ff ect

10.7498/aps.66.226601

?國家自然科學基金(批準號:11574154)資助的課題.

?通信作者.E-mail:phyzlf@njnu.edu.cn