Dirac光子晶體?

王海嘯 徐林 蔣建華2)

1)(蘇州大學物理與光電.能源學部,蘇州 215006)2)(蘇州大學,2011蘇州納米科技協同創新中心,蘇州 215006)

Dirac光子晶體?

王海嘯1)?徐林1)蔣建華1)2)?

1)(蘇州大學物理與光電.能源學部,蘇州 215006)2)(蘇州大學,2011蘇州納米科技協同創新中心,蘇州 215006)

(2017年8月15日收到;2017年10月31日收到修改稿)

Dirac費米子作為粒子物理中的基本粒子之一,其理論在近年來蓬勃發展的拓撲電子理論領域中被廣泛提及并用來刻畫具有Dirac費米子性質的電子態.這種特殊的能態通常被稱為Dirac點,在能譜上表現為兩條不同能帶之間的線性交叉點.由于Dirac點往往是發生拓撲相變的轉變點,因而也被視為實現各種拓撲態的重要母態.作為可與拓撲電子體系類比的拓撲光子晶體因其獨特的潛在應用價值也受到人們的廣泛關注,實現包含Dirac點的光子能帶已成為研究拓撲光子晶體的核心課題.本文基于電子的拓撲理論,簡要地回顧了Dirac點在光子系統中的研究進展,特別介紹了如何在光子晶體中利用不同晶格對稱性實現在高對稱點/線上的Dirac點,以及由Dirac點衍生的Weyl點.

光子晶體,Dirac點,拓撲能帶,量子自旋霍爾效應

1 引 言

1928年,Dirac[1]給出了自旋為1/2的粒子在相對論量子力學下的波動方程,方程的解代表著一類基本粒子,稱為Dirac費米子(包含電子和正電子).特別地,當粒子的質量為零時,粒子的能量與動量呈現出線性關系.通常人們將具有這種線性色散關系的粒子稱為無質量Dirac費米子.在凝聚態物理中,無質量Dirac費米子的色散關系也用于描述某些特殊的電子態,這些電子態被稱為Dirac點.其中最為人們所熟悉的就是石墨烯,它的能帶結構在布里淵區邊界K(K′)處具有線性色散關系[2].這種電子態具有一些非常奇特的傳輸性質,例如室溫量子霍爾效應[3]和Klein隧穿[4]等.

近年來拓撲電子理論在凝聚態領域的迅速發展使得Dirac方程又重新煥發出活力,系統的研究表明Dirac方程對理解拓撲絕緣體和拓撲超導體的性質和相變具有重要意義[5].人們發現,在連續變化下只要能帶之間的帶隙不閉合,那么系統的拓撲性質就不會發生改變.換言之,能帶拓撲性質的改變總是需要經歷能帶閉合-打開的過程.Dirac點作為能帶的線性交叉點,是能帶閉合-打開的轉變點,無疑在拓撲能帶理論中占據著舉足輕重的地位.歷史上,Dirac點是獲得非平庸拓撲能帶的一個重要途徑.早在1988年,普林斯頓大學的霍爾丹(F.D.M.Haldane)首次在六角蜂窩晶格中給出了量子反常霍爾效應(quantum anomalous Hall e ff ect)的玩具模型[6].這個模型可以無需借助外磁場而實現具有非平庸陳數的拓撲能帶,其性質類似于外磁場為零的量子霍爾效應,對應系統的邊界上有一個單向傳輸的邊界態出現.在Haldane模型中,從平庸能帶到非平庸能帶的轉變就是通過打開蜂窩晶格中Dirac點的能隙實現的.需要說明的是,在Haldane模型中只有兩種打開Dirac點能隙的方式:第一種方式是破缺空間反映對稱性,它導致一個平庸的能帶;第二種方式是破缺時間反演對稱性,它導致一個拓撲非平庸的能帶.

然而,Haldane模型并未考慮電子的自旋.直到2005年,賓夕法尼亞大學的凱恩(C.L.Kane)和米爾(E.J.Mele)在石墨烯系統中發現把Haldane模型擴展到包含電子自旋自由度后,系統可以出現新的拓撲相,稱之為Z2拓撲相[7,8].這種特殊的拓撲相并不破缺時間反演對稱性,卻在系統邊界上也存在著一對傳播方向相反,自旋極化相反的邊界態.由于時間反演對稱性的保護,它們能相互穩定共存,即使在無序系統中它們仍然能夠保持單向傳輸且不發生背向散射.這是另一個打開Dirac點的能隙之后導致非平庸的拓撲能帶的例子.此后,人們又發現三維的拓撲絕緣體也可以通過打開三維Dirac點的能隙來實現[9].

由以上這些例子可見,在Dirac方程中引入非零質量項而打開Dirac點能隙,可以使系統發生拓撲相變.那么,如果不打開Dirac點的能隙能否實現系統的拓撲相變呢？答案是肯定的.早在Dirac方程被提出的第二年,Weyl就指出Dirac方程無質量的解描述的是一對新粒子,這一對新粒子具有相反的手性,也就是今天人們常說的Weyl費米子[10].所以,具有四重簡并(包含自旋和軌道兩個自由度)的Dirac點也可以看成是一對具有相反手性的Weyl點組合而成;而當系統不再具有某種對稱性時,手性相反的Weyl費米子的能譜將不再重疊,Dirac點也就會退化成為一對手性相反的Weyl點.

由此可見,無論是拓撲絕緣體,還是近來廣受關注的Weyl拓撲節點,都可以通過Dirac點來實現,因此,Dirac點作為拓撲態的一個母態,對于研究拓撲物質態和拓撲相變具有極其重要的意義.

Dirac點在電子系統中的廣泛研究也吸引了光學領域研究人員的注意[11?20].因為從能帶圖像和布洛赫定理來看,光子晶體和原子晶體具有很多的相似性.然而需要指出的是,電子作為費米子具有自旋1/2的獨特內稟屬性.由于此獨特的性質,Kramers定理導致電子在時間反演對稱的波矢下具有天然的二重簡并,而光子作為玻色子則不具有這樣的二重簡并.事實上,實現光子拓撲態的核心挑戰之一就是要實現光子能帶的二重簡并.

為此,人們首先根據光特有的偏振特性,利用TE+TM/TE-TM(TE和TM分別表示橫向電場和橫向磁場模式)[14]混合模式、TM/TE模式[15],左旋光/右旋光[16]等在光學系統中實現了特殊材料/超材料中的二重簡并,并借助光子晶體實現了光學系統中的Dirac點和拓撲物質態.我們把利用光學系統的偏振自由度實現二重簡的拓撲光子系統以及實現具有陳數的光子系統的研究[12,13]稱為拓撲光子學研究的第一階段.由于這些研究往往需要具有特殊性質的材料,如磁光材料、具有磁電耦合的材料,具有電磁對偶對稱性的材料等,而難以有廣闊的應用前景.從2015年開始,人們開始提出各種具有特別晶格對稱性的光子晶體[18?22],這些光子晶體并不需要特殊的材料,只用普通的介質材料即可實現光子的拓撲態.與以往利用光偏振特性的研究不同,利用晶格對稱性可以有效地實現光子能譜在特殊波矢上的二重簡并,并進而實現光子的Dirac點.通過打開Dirac點可以實現特殊的拓撲光子態.本文著重介紹基于點群和非點群的對稱性來實現光子晶體中的Dirac點和拓撲光子態的方法,首先討論二維的光子晶體,再擴展到三維的光子晶體.

在開始之前,需要先澄清用詞方面的一些混淆.本文中的Dirac點是具有四重簡并的線性能譜交叉點.因為Dirac的原始論文考慮的正是一個具有四重自由度的系統:正電子有兩重自由度(自旋1/2),電子也有兩重自由度,一共有四重自由度.與此相對的,Weyl點指的是具有兩重簡并的線性交叉點(也可以是拋物線交叉點,這里暫不考慮).在二維系統中,由于無法定義Weyl點,稱所有的線性色散交叉點為Dirac點.若二維系統具有四重簡并的Dirac點,那么就稱之為雙Dirac點.

2 二維Dirac光子態

2.1 雙Dirac點及相圖

理論上最早給出二維介質光子晶體拓撲絕緣體的是日本國家材料科學研究所(NIMS)的Hu研究組[18],他們在蜂窩點陣結構中,通過能帶折疊的方式將K和K′點的Dirac點折疊到布里淵區中心,獲得了雙Dirac點.通過變形點陣結構可以打開雙Dirac點的帶隙,并實現能帶反轉,由此實現光子的量子自旋霍爾效應.這里雙Dirac點出現的條件是晶格具有C6旋轉對稱性.因為在二維點群中,只有具有C6對稱性的三角晶格系統才會在布里淵區中心出現雙Dirac點[23,24].

圖1 自然界中廣泛存在的核殼結構 (a)海鼠;(b)海鼠體表刺的透射電子顯像;(c)海鼠體表的刺;(d)蛋白石頭;(e)蛋白石膠體晶體的掃描電子顯像Fig.1.Hexagonal photonic crystals in nature:(a)The sea mouse(Aphroditidae);(b)the transmission electron micrograph of the sea mouse spine;(c)images of a sea mouse spine illuminated with light;(d)opal;(e)the SEM images of the colloidal crystal in opal.

2016年,Xu等[20]利用核-殼結構的二維光子晶體給出了另一種實現光子的量子自旋霍爾效應的例子.核-殼結構構成的三角晶格廣泛存在于自然界中,包括膠體晶體及海鼠皮膚表面凸起的晶格結構[25,26],都是這種結構(圖1).

為方便表述二維核-殼結構光子晶體的拓撲相變機理,在這里核-殼的內徑和外徑分別設為R1和R2,晶格常數為a=1,核殼結構及背景材料的介電常數分別為ε1=1和ε2=12(見圖2(a)插圖).利用基于有限元計算方法的COMSOL軟件可以計算二維光子晶體的能帶結構及其場圖,不同宇稱能帶之間的偶然簡并則可以通過調節核殼結構的內外徑來實現.特別地,當結構參數R2/R1=0.26/0.45時,在Γ點出現了p帶和d帶的四重簡并態,就是系統發生拓撲轉變的雙Dirac點(圖2(b)).具體而言,奇宇稱的兩個簡并態是兩個p波,如px和py態;而偶宇稱的兩個簡并態是兩個d波,如dx2?y2和dxy態.一個更好的表象是把它們重新組合成如下的形式:奇宇稱的兩個態p+=px+ipy和p?=px?ipy,二者可以通過時間反演對稱操作相互聯系,類比電子系統中的自旋上和自旋下的兩個簡并態,將其稱為p帶的贗自旋.類似地,偶宇稱的兩個態可以表示d+=dx2?y2+idxy及d?=dx2?y2? idxy,分別對應d帶的贗自旋上態和贗自旋下態[18].

由于Z2拓撲相是打開雙Dirac點得到的,所以我們有必要采用電子能帶論發展起來的k·p理論來討論這些能帶之間(p帶和d帶)的相互作用(k·p理論在Maxwell方程中的正確應用及其對量子自旋霍爾效應的解釋請參考文獻[20]).首先,TM模式下的Maxwell方程可以寫成:

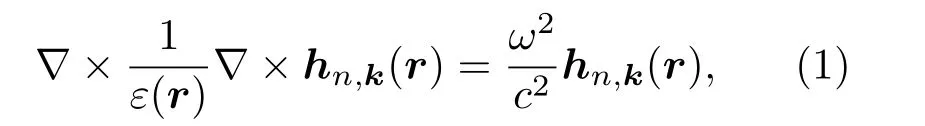
這里的n是光子的能帶指標,hn,k(r)是光子磁場的布洛赫函數,它的歸一化表達式是

積分區域u.c.代表的是一個原胞單元.(1)式中的厄密算符可以作為光子系統的哈密頓量(目前有一些論文在k·p方法中使用的光子“哈密頓量”不是厄密算符,正確的k·p方法見文獻[20]),將布洛赫函數hn,k(r)在Γ點展開,可以得到系統的k·p哈密頓量:

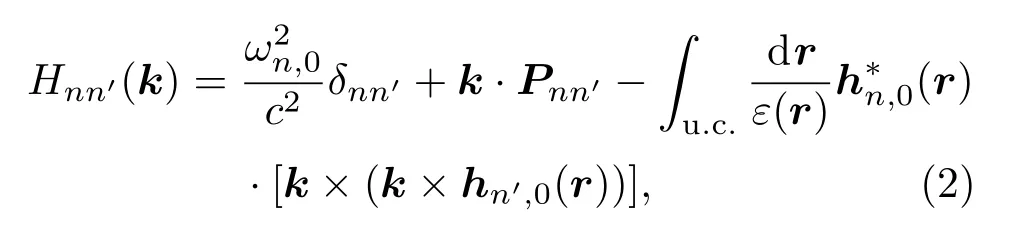
這里的ωn,0表示第n條能帶在Γ點的本征頻率,動量P矩陣元的表達式為

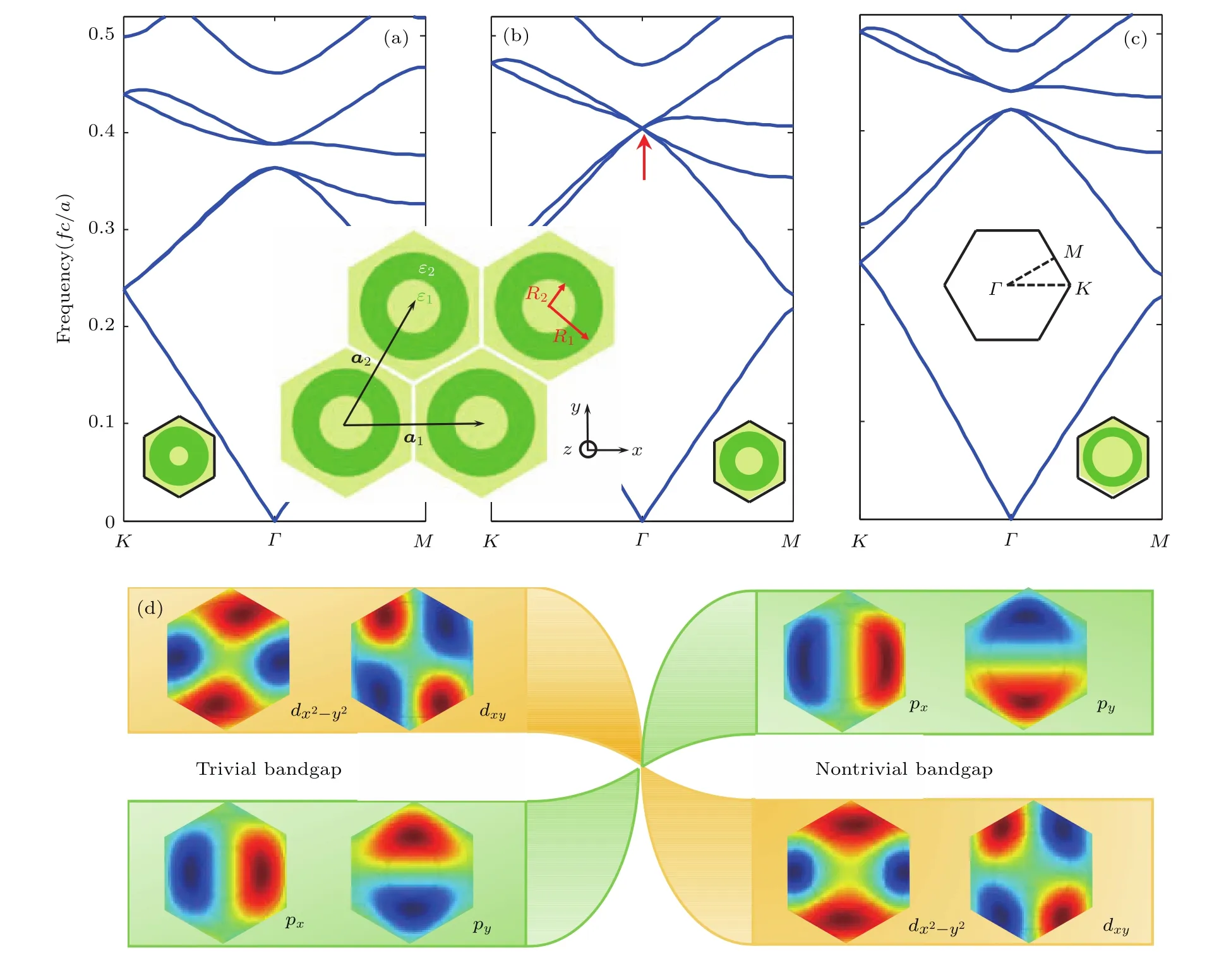
圖2 核-殼結構的能帶圖及拓撲相變示意圖 (a)R2/R1=0.2/0.45,正常的光子絕緣態;(b)R2/R1=0.26/0.45,Dirac光子態;(b)R2/R1=0.3/0.45,量子自旋光子霍爾態;(d)相變示意圖,左側為能帶圖(a)的第2,3與4,5條能帶在Γ點的電場場圖,右側為能帶圖(c)的第2,3與4,5條能帶在Γ點的電場場圖Fig.2.The band structure of core-shell photonic crystal and the schematic of topological phase diagram:(a)R2/R1=0.2/0.45,normal photonic insulator state;(b)R2/R1=0.26/0.45,Dirac photonic state;(c)R2/R1=0.3/0.45,quantum spin hall state;(d)schematic of topological phase transfer diagram,left panel is electric field pattern of the 2nd,3rdand 4th,5thband at Γ point in(a);right panel is electric field pattern of the 2nd,3rdand 4th,5thband at Γ point in(c).

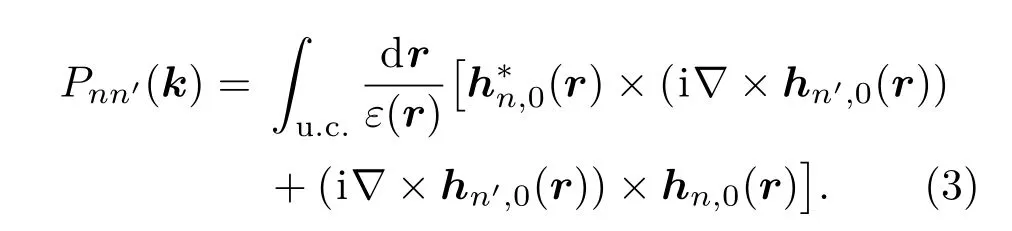
注意到只有當第n和第n′條能帶的宇稱不同時,動量P的矩陣元才不等于零.根據k·p理論,有效哈密頓量在(p+,d+,p?,d?)T表象下的形式是:

式中的k±=kx±iky,A是不同態之間的耦合系數;顯然,只有相同的自旋極化方向的p態(d態)之間(即p+與p?,d+與d?)才會有耦合.需要指出的是,(4)式給出的哈密頓量與電子系統中Bernevig-Hughes-Zhang(BHZ)模型[27]給出的哈密頓量相似,其中的兩個方塊子矩陣分別對應贗自旋上和贗自旋下的有質量的Dirac方程.這一對贗自旋光子對是由時間反演對稱操作來聯系的,這保證了整個系統仍然滿足時間反演對稱性.所以,若把p帶作為價帶,d帶作為導帶,那么類比電子系統中的BHZ模型,對應的(4)式就可以描述光子的量子自旋霍爾效應:當ωp＜ωd時系統對應的就是拓撲平庸態;當ωp＞ωd時,系統在Γ點處發生了pd宇稱反轉,這就直接導致了光子的Z2拓撲態;當ωp=ωd=ω0時,在Γ點就會出現一個四重簡并點,對應于雙Dirac點,即拓撲相變點.

雖然增加或者減小R2/R1的比值時均會打開p帶和d帶之間的能隙,但根據以上的理論模型分析,有一種類型的能隙是平庸的,另一種類型的能隙則是拓撲的,其關鍵的點就是看系統是否發生宇稱反轉(p-d反轉).如圖2(d)所示,當R2/R1＜0.25/0.46,p帶的頻率較低(ωp＜ωd),系統對應于普通光子絕緣體;當R2/R1＞0.25/0.46時,d帶的頻率較低(ωp＞ωd),對應光子拓撲絕緣體.

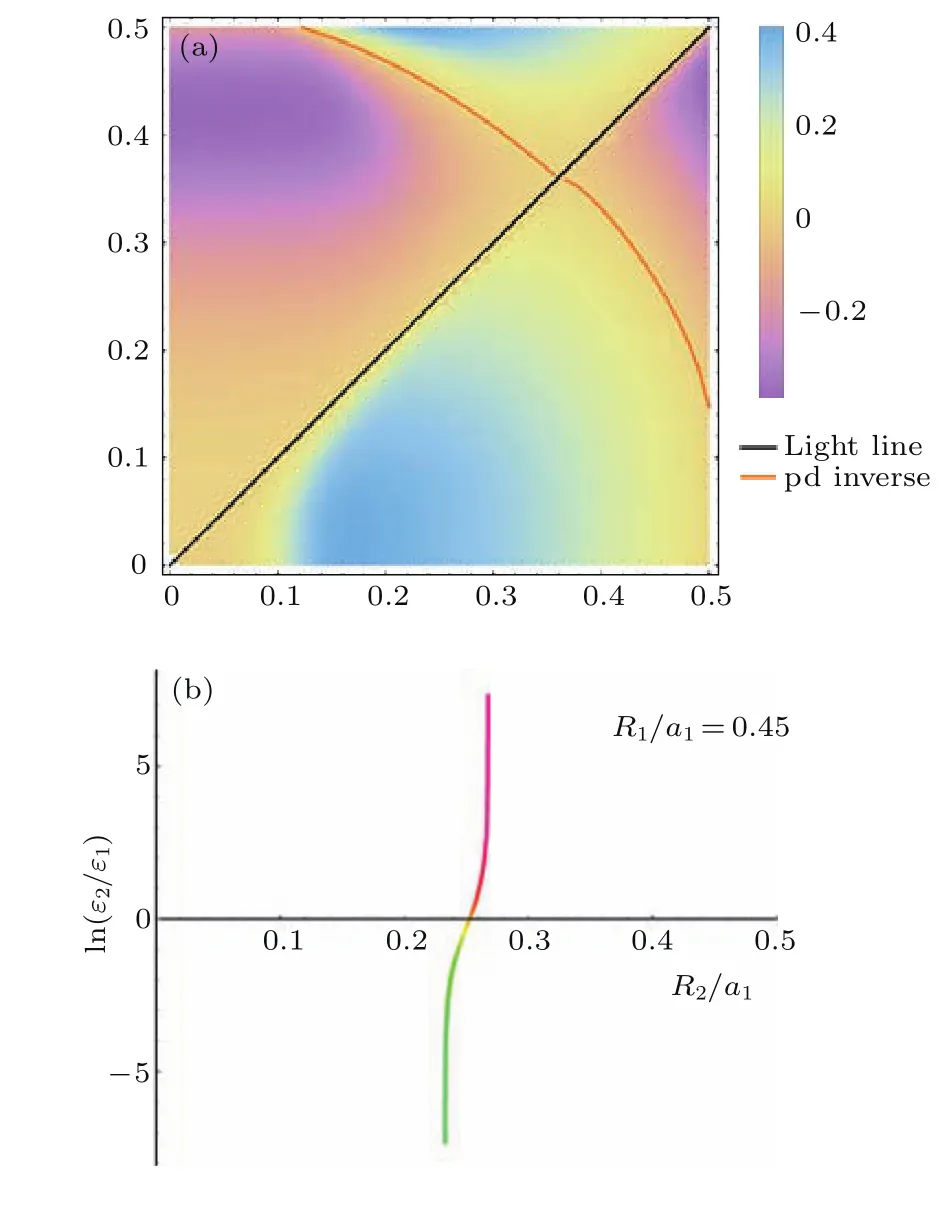
圖3 核-殼結構的相圖 (a)p-d反轉導致的光子Z2拓撲絕緣體在R1-R2參數空間的相圖,對角線以上及以下分別表示正結構及反結構;橙色區域表示p-d正常,對應于正常光子絕緣態,藍色區域表示p-d反轉,對應量子自旋霍爾態,橙色實線表示p-d四重簡并態,即雙Dirac點;(b)固定外徑R1=0.45a,出現雙Dirac點對應的介電常數的比率ln(ε1/ε2)與內徑R2的關系Fig.3.Phase diagram of core-shell structure:(a)Phase diagram of the p-d inversion-induced photonic Z2topological insulator in the R1-R2parameter space,the diagonal line represents the homogenous limit which separates the normal and reversed structures in the upper and lower triangular regions,the orange region represents that the p bands are lower than the d band at Γ point,whereas the blue region stands for the photonic analog of the Z2topological insulators with the p bands above the d bands at Γ point,the p-d band degeneracy at the Γ point is labeled by black line;(b)relationship between ln(ε1/ε2)and the critical inner radius R2 where the double Dirac cone emerges,the outer radius of the hollow cylinder is fixed at R1=0.45a.

考慮到可以通過結構參數實現光子能帶的反轉,為使結果更具有普遍性,我們也討論了R1和R2獨立改變對能帶反轉的影響,得到了能帶反轉的相圖(圖3(a)),圖中藍色區域表示p-d反轉,橙色區域表示p-d正常.由此可見,二維三角晶格的拓撲相變在很大的參數范圍內具有可調性,甚至在反結構(這里定義ε1和ε2交換的結構為反結構,即ε1=12＞ε2=1)中也能實現能帶宇稱的反轉.同時,我們還討論了ε1和ε2的比值對雙Dirac點出現時的幾何參數R1和R2的影響(圖3(b)).通常情況下,光子晶體的能隙會隨著不同介質的介電常數比值的增加而增加;但有意思的是,當固定外徑R1(=0.45a)調節內徑R2及ε1/ε2以獲得雙Dirac點時,我們發現內徑的臨界值在ε1/ε2很大的一段范圍變化很小,這說明對介電常數對雙Dirac點的影響遠小于幾何參數.

需要注意的是,這里的物理和文獻[18]中考慮的蜂窩晶格很不一樣,蜂窩晶格一定會出現雙Dirac點,可以把這種對稱性導致的雙Dirac點稱之為必然簡并點.然而,核-殼結構中雙Dirac點的出現具有一定的偶然性,不受簡單因素的決定.對于二維核殼光子晶體,可以認為每個核殼都是一個共振腔,其中的局域態可以認為是Mie散射造成準局域態[28].該光子晶體中的光子能帶可以看成是相鄰格點中的準局域態之間的相互耦合／雜化導致的.通過調節球殼結構的內徑和外徑,可以有效地調節p態和d態的能量和場分布,由此有效地調節p帶和d帶的能量,從而實現宇稱反轉的拓撲光子態.

2.2 邊界態及贗自旋選擇的單向傳輸

現在我們來討論光子拓撲絕緣體的邊界態性質.在上述核-殼系統中,我們可以選取兩種能隙匹配且具有不同拓撲性質的光子晶體實現具有拓撲保護的邊界態,它的Z2拓撲相受到了贗時間反演對稱性的保護,該贗時間反演對稱算符可以表示成Tp=iσyK(K表示復共軛算符),其中的σy項可以寫成C6對稱操作的線性組合使得T2p=?1.這里需要說明的是,只要系統具有二重簡并態,我們總是可以構造出這種反幺正算符.因此,若要在光子晶體中模擬Z2的拓撲,關鍵就是要找到兩種不同宇稱的雙重簡并態.在這里,我們選取兩種尺寸相近、拓撲性質不同的光子晶體(Z2=0與Z2=1)來產生邊界態(圖4(a)與圖4(b)).

從圖4可以看到,A點對應邊界態的場圖的坡印廷矢量方向是順時針,代表自旋上;B點對應邊界態場圖的坡印廷矢量方向是逆時針,代表自旋下;他們是由時間反演對稱性聯系的.值得注意的是在圖4(c)中,由于Γ點處的p態及d態的二重簡并是由點群對稱性保護的,而在由不同結構組成的邊界明顯地破壞了C6的對稱性,這使得原本是線性交叉的邊界態打開了一個微小的能隙,計算模擬表明這個打開的能隙與邊界破壞C6對稱性的程度有密切的關系.雖然表面態打開了一個小的能隙,然而這些光子晶體體能帶的拓撲性質是沒有歧義的(雖然目前的理論還沒有嚴格證明這一點,我們最新的基于Berry phase的計算已經證明了非平庸的拓撲數).

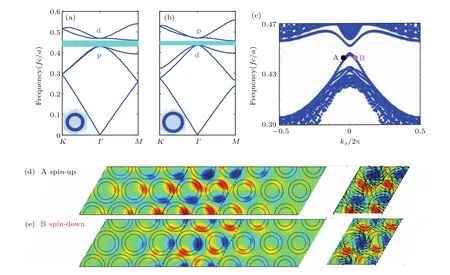
圖4 拓撲邊界態 (a)p-d正常態的能帶結構,R1=0.4a,R2=0.26a;(b)p-d反轉態的能帶結構,R1=0.45a,R2=0.32a,共同能隙由青色的區域標出;(c)兩種不同光子晶體構成的投影能帶;(d)A點對應邊界處的電場分布,對應的坡印廷矢量方向為順時針,代表自旋向上;(e)B點對應邊界處的電場分布,對應的坡印廷矢量方向為逆時針,代表自旋向下Fig.4.Topology-induced edge states:(a)The normal band structure with R1=0.4a and R2=0.26a;(b)the normal band structure with R1=0.45a and R2=0.32a,the common complete band gap is marked with the cyan ribbon;(c)the projected band structure of two photonic crystals with oblique line edge,A and B mostly comprise of the pseudo-spin-up and spin-down edge states,respectively;(d)and(e)are the Ez field pattern of A and B.

3 三維Dirac光子態

3.1 受點群對稱性保護的三維第一類Dirac光子態

在二維情況下,我們利用點群對稱性制造光子的自旋自由度,成功地實現光子的量子自旋霍爾效應,那么有沒有可能將上述結果推廣到三維系統中呢？答案是肯定的.因著真正的材料總是三維,在三維光子系統中實現Dirac點具有重要的現實意義.然而,若要類比電子系統在光子晶體實現三維Dirac點至少有兩個問題亟待解決:1)電子與光子兩種粒子的性質不同,光子是玻色子,缺少自旋自由度;2)光子能帶形成的機理與電子也不同,電子能帶可以被認為是不同局域原子軌道混合的結果,光子能帶是由多重布拉格散射造成的結果,缺少局域軌道自由度的圖像.

為此,我們在二維核-殼結構的基礎上,提出了由兩個中空介質柱組成結構單位,構成三維六角晶格光子晶體(圖5(a)和(b)).根據文獻[28],光子系統中的Mie散射共振看作是光子的局域軌道,不同的光子能態可以看作是不同波之間的Mie散射共振.這里將中空柱子的Mie散射共振看作是光子的局域軌道;那么,類比二維的情況,光子的p帶和d帶就可以被認為是來自p波和d波的Mie散射共振.需要再次強調的是,只有C6v對稱群包含兩個二重簡并的表象,并且這兩個二重表象具有相反的宇稱.根據宇稱的選擇定則,兩個宇稱相反的態之間的相互作用必定導致線性色散.因此,對三維情況而言,只有在動量空間滿足六重旋轉對稱操作的不變高對稱線上,才可能出現穩定的Dirac點.事實上,我們發現在ΓA這條高對稱線上p帶及d帶是二重簡并的(圖5(c)),這與上述的判斷是一致的.不僅如此,理論計算也發現三維Dirac點總是出現在ΓA或KH這條線上;甚至移除兩個中空圓柱之間的六根柱子后,在ΓA或KH這條線上的Dirac點也是存在的.這是因為在六角晶格中ΓA和KH都是動量空間中滿足六重旋轉不變的高對稱線.需要特別指出的是,光子晶體中的這種性質與電子系統具有巨大的差異:在電子系統中,具有C3,C4和C6對稱操作的結構都可以出現穩定的Dirac點[29].由于在布里淵區高對稱點處的四重簡并態總是不穩定的,C6點群對稱性的引入使得Dirac點變得相當的穩定.

為證明以上的判斷,我們仿照二維的例子,選取(d+,p+,d?,p?)T作為系統k·p哈密頓量的基矢量. 首先,根據|px〉,|py〉,|dx2?y2〉,|dxy〉波函數的對稱性及動量算符Px和Py的作用形式,可以得到

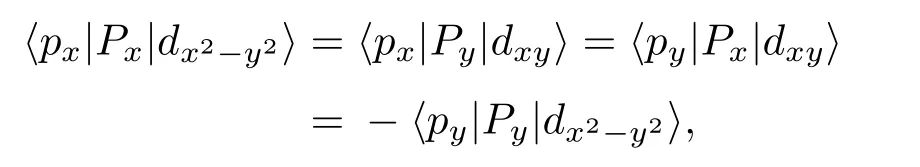
因此,〈p+|H|d+〉=〈p?|H|d?〉?=A||k||eiθk, 這里θk=Arg[kx+iky]是x-y平面內的幅角,A||=〈px|Px|dx2?y2〉.

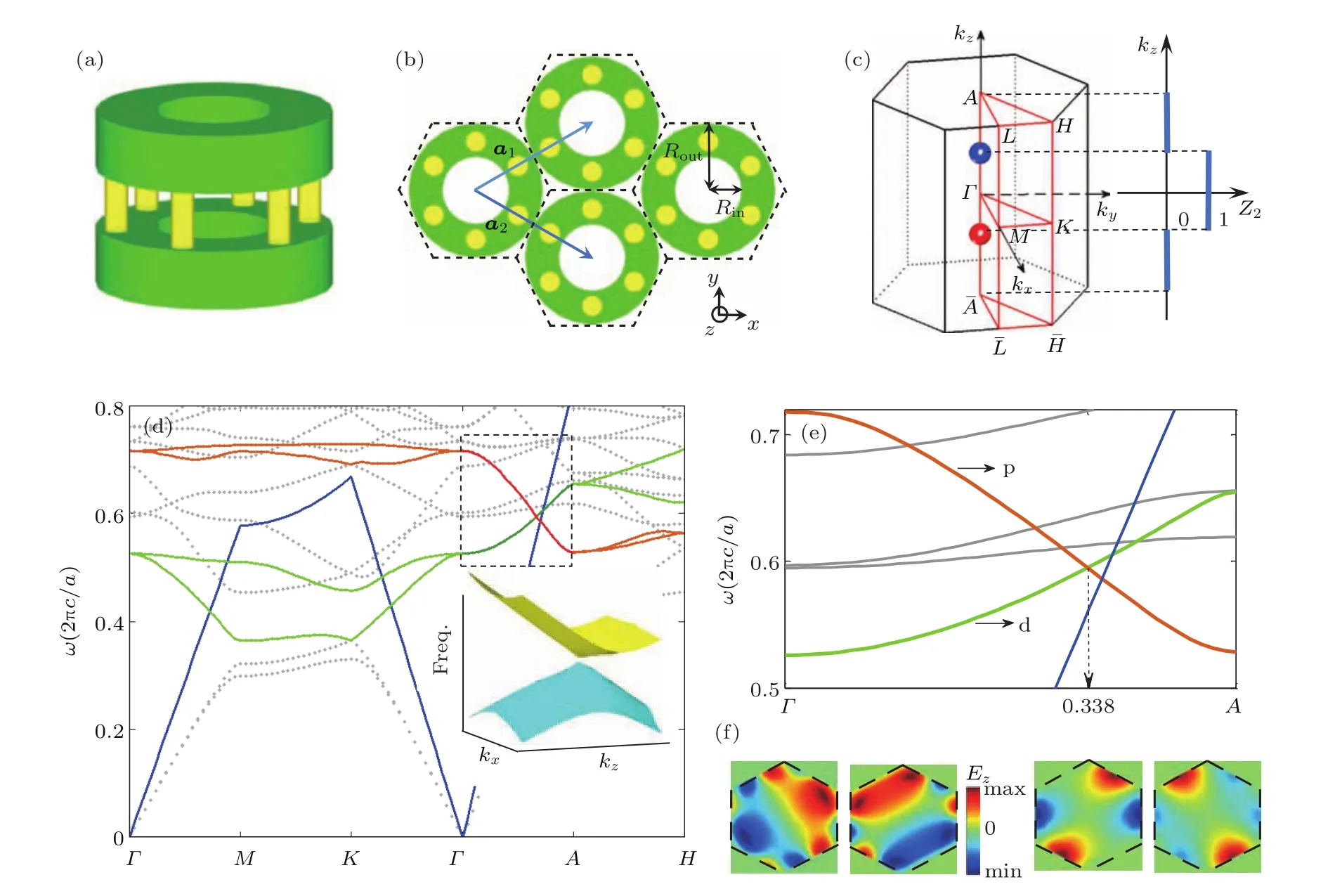
圖5 點群對稱性導致的三維Dirac光子晶體 (a)實空間六角晶格結構光子晶體原胞,中空圓柱及六根柱子均是用相同介質構成;(b)六角晶格結構的俯視圖,其中a是xy平面內的晶格常數,a1和a2是晶格的基矢量.高度為h=0.6a,外徑和內徑分別為Rout=0.5a和Rin=0.45a,高度為0.4a;(c)倒空間中的第一布里淵區,紅色及藍色小球分別代表不同拓撲電荷的Dirac點;(d)六角晶格光子能帶;插圖為Dirac點三維色散結構;(e)ΓA高對稱線上的能帶,其中紅線代表的p帶和=綠線代表的d帶在處相交;(f)Γ點p帶和d帶在xy平面內的場圖Fig.5.Three dimensional Dirac photonic crystal induced by point group symmetry:(a)Structure in real-space unit cell of hexagonal photonic crystals,hollow cylinder and micropillars are made of the same material with isotropic permittivity;(b)top-down view of hexagonal photonic crystal,a1and a2are the two lattice vectors in the x-y plane,the height of each unit cell is h=0.6a,the outer and inner radii of the hollow cylinder are Rout=0.5a and Rin=0.45a,respectively,whereas its height is 0.4a;(c) first Brillouin zone with a pair of Dirac points along the Γ-A line,a Dirac point with di ff erent topological charge is labeled as a red and blue point;(d)photonic band structure of a hexagonal photonic crystal with C6and inversion symmetry,inset is the dispersion of Dirac point with Kz＞0;(e)band structure along line,the p bands(red)cross the d bands(green)at(0,0,Kz)with Kz=0.338;(f)Ez field pro file in the x-y plane of p bands and d bands.

最終,系統在基矢量(d+,p+,d?,p?)T表象下的k·p哈密頓量:

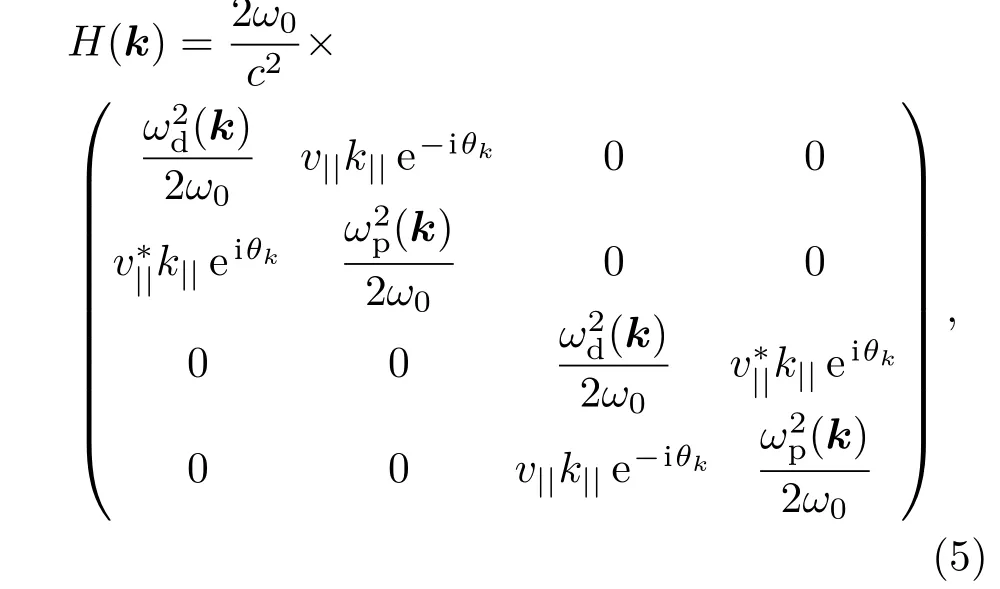
其中ω0表示Dirac點對應的頻率,是在x-y平面內的群速度分量,它是kz的函數,可以發現對每一個給定的kz,(5)式都是代表一種拓撲平庸或非平庸的系統:當|kz|＞Kz時,ωp,0(kz)＜ωd,0(kz),在Γ點p態頻率比d態頻率要低,系統對應的將是拓撲平庸態(普通絕緣體);當|kz|＜Kz時,ωp,0(kz)＞ωd,0(kz),在Γ點p態頻率比d態頻率要高,系統對應的將是拓撲態;當|kz|=Kz時,ωp,0(kz)=ωd,0(kz),即Dirac點.需要注意的是,雖然這種Dirac點是一種偶然簡并導致的四重簡并點,其位置Kz是隨著結構參數的改變而改變的,但只要p帶和d帶在Γ點交換頻率順序,這種偶然簡并將會是不可避免的.以三維Dirac點作為臨界點,在|kz|=Kz的兩邊將會出現兩種不同拓撲性質的絕緣體.由此可見,三維Dirac點是相應二維系統拓撲相變臨界點.

3.2 受非點群對稱性保護的三維第二類Dirac光子態

通過點群對稱性,我們已經得到了相當穩定的三維Dirac點.在這部分,我們將介紹基于非點群對稱性引入的三維Dirac點,所謂非點群對稱操作包括旋轉(或鏡面)加上平移(小于晶格常數距離)(圖6(a)).作為例子,我們給出了的原胞中都有兩個垂直且完全相同的介質塊(圖6(b)),對應的介電常數εb,背景填充材料的介電常數εm的在三個方向上的晶格常數都為a=1,該結構關鍵的對稱性包括:1)二重旋轉對稱性Sx:=(x,y,z)→(0.5+x,0.5?y,0.5?z)及Sy:=(x,y,z)→(0.5?x,0.5+y,0.5?z);2)繞著z軸180?旋轉的C2:=(x,y,z)→(?x,?y,z);3)時間反演對稱性T:t→?t;4)三個方向的鏡面對稱性M1:=(x,y,z)→(y,x,z);M2:=(x,y,z)→(?y,?x,z);M3:=(x,y,z)→(y,x,?z).在此,我們采用MIT Photonic Band(MPB)軟件包來計算三維光子晶體的能譜,結果顯示,能譜在kx=π面上都具有二重簡并度(圖6(c)),并且在高對稱線MA上具有兩個四重簡并點(Dirac點),對應的光子能態呈現出p態和d態(圖6(d)).

為了說明在kx=π(ky=π)面上的二重簡并,構造以下反幺正算符:,其中的T是時間反演算符,相當于對光子的布洛赫波函數做復共軛運算;可以發現,就是相當于一個空間平移矢量r=(1,0,0),那么作用兩次算符在布洛赫的波函數上,即eikxψnk(r).顯然在kx=π的平面上,根據Kramers簡并條件,所有在kx=π的平面上的布洛赫態將是二重簡并態.類似地,也可以證明,所有在ky=π的平面上的布洛赫態將也是二重簡并態.這表明利用非點群對稱性也可以增加光子能帶的簡并度,以此獲得光子贗自旋的自由度.

另一方面,實現三維光子晶體Dirac點還要給出宇稱反轉的圖像.在這里通過二重旋轉軸C2來定義xy平面內的宇稱;注意到兩個正交的旋轉對稱算符滿足如下對易關系是:SxSy=T010C2及SxSy=T100C2.因此,在MA這條高對稱線上,我們可以得到對易關系式,也就是說在MA這條高對稱線上算符與算符和C2對稱操作都是對易的.所以,任意兩個簡并態都會具有相同的C2的本征值c2,而這個本征值c2=±1就可以被我們用來標記xy平面內的宇稱.由此,當任意兩個在MA線上具有不同宇稱的能帶的交叉點就是三維的Dirac點,對應Dirac點的拓撲電荷[30]為,這里的表示Dirac點較低頻率能帶的宇稱,k0表示Dirac點所對應波矢.根據圖6在最低的六條能帶中總共有四個拓撲電荷NDP=±1的Dirac點,他們都是由雙重簡并的p波及d波的能帶線性交叉形成的.

值得說明的是,這種利用非點群對稱性引入得的三維Dirac點并不十分依賴于結構單位的形狀大小以及介質的參數,任意兩種不同宇稱的能帶交叉點都是Dirac點.由此可見,基于非點群對稱的結構設計是一種非常有效的方法來實現三維Dirac點.

圖6 非點群對稱性導致的三維Dirac光子晶體 (a)非點群操作示意圖;(b)左側為三維結構原胞(邊界有黑色實線標注),右側為兩種正交旋轉對稱操作Sx和Sy的示意圖;(c)kx=π光子能帶,右側為高對稱線MA上的Dirac點;(d)p帶和d帶的二重簡并的磁場場圖;相關參數0.5a,w=0.2a,h=0.5a,材料的介電常數分別是εb=16,εm=1.9;(e)I型Dirac點的三維色散;(f)II型Dirac點的三維色散Fig.6.Three dimensional Dirac photonic crystal induced by non-symmorphic symmetry:(a)Schematic of nonsymmorphic symmetry operation;(b)left is 3D structure of a unit cell(boundaries are indicated by black lines),right is Illustration of the two orthogonal screw symmetries Sxand Syin top-down view;(c)photonic band structure with kx=π,parity inversion on the MA line;(d)left and right are magnetic field pro files of the p and d wave doublet,respectively,parameters0.5a,w=0.2a,h=0.5a,and permittivity εb=16 and εm=1.9;(e)3D dispersion of type-I Dirac point;(f)3D dispersion of type-II Dirac point.

4 三維Weyl光子態

在2013年,麻省理工學院的Lu等[31]在破缺空間反映對稱性的螺旋二十四面體光子晶體中發現了Weyl點.然而,在這種依賴于特定結構的Weyl點并不具有普遍性.另一方面,我們知道三維Dirac點可看作是由一對手性相反的Weyl點構成.因此,在破缺系統的某些對稱性后,三維Dirac點將會演化為一對手性相反的Weyl點,相應的拓撲不變量也將由Z2數變為陳數.根據這個思路,我們以上述兩種受對稱性保護的三維Dirac點為例,來闡述如何由Dirac點得到Weyl點.

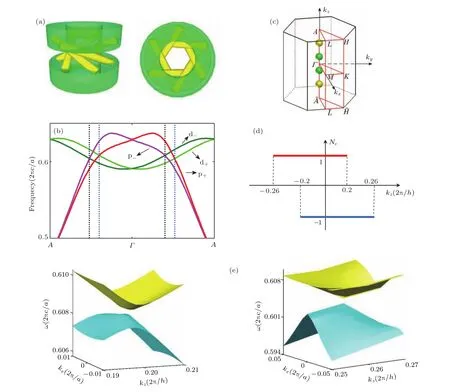
圖7 保持C6對稱性且破缺空間反演對稱性后的六角晶格光子晶體 (a)原胞結構的側視圖及俯視圖;(b)kz方向上的光子能帶(忽略其他不相干的能帶),存在著兩對Weyl點;(c)第一布里淵區內Weyl點的示意圖,綠色和黃色小球分別代表手性不同的Weyl點;(d)陳數分布圖:紅線表示p?-d?的能帶,藍線表示p+-d+的能帶;(e)兩個Weyl點的附近光子三維色散Fig.7.Inversion symmetry broken hexagonal photonic crystal with C6symmetry:(a)Lateral(left)and top-down(right)views of the structure in a real-space unit cell;(b)photonic bands along the kz-direction,two pairs of Weyl points are found;(c)depicting the four Weyl points in the first Brillouin zone,green(yellow)spheres denote Weyl points with chirality ?1(+1);(d)Chern number Ncfor the p+-d+bands below the Weyl points(blue)and for the p?-d?bands below the Weyl points(red);(e)photonic spectrum near the two Weyl points,left for WP at(0,0,Kz1);right for Weyl points at(0,0,Kz2).

4.1 受點群對稱性保護的Weyl光子態

對于由點群對稱性保護的三維Dirac點,我們知道ΓA高對稱線上具有二重簡并的p帶和d帶是由C6及z方向上的反映對稱性保護的,因此通過破壞旋轉連接兩個中空圓柱的六根棍子來破壞系統的空間反映對稱性,使得p+帶和p?帶及d+帶和d?帶解簡并,同時由于系統仍然存在C6的對稱性,使得具有不同C6操作本征的四條能帶將仍然彼此交叉,所以空間反演對稱性的破壞相當于在原來的系統中引入一個質量項.這時,一對Dirac點將會分裂形成四個Weyl點,這時描述系統的拓撲不變量就是陳數,根據圖7在0.2＜|kz|＜0.26的范圍內,總的陳數是非零的,這種陳數的分布是Z2Dirac點導致的顯著特征.這一影響也使得邊界態成為單向傳輸的邊界態.

4.2 受非點群對稱性保護的Weyl光子態

對于由非點群對稱性保護的Dirac點,為了獲得Weyl點所需要破缺對稱性包括：旋轉對稱性(Sx及Sy),三個鏡面對稱性(M1,M2,M3)以及系統的空間反演對稱性P,而只保留180?旋轉對稱性.顯然,破壞了系統的旋轉對稱性會解除在MA高對稱性上的二重簡并性;另一方面,180?旋轉對稱性仍然保證在MA這條高對稱線上不同宇稱能帶的偶然線性交叉,這種線性交叉就是Weyl點.從圖8可以發現總共有三對Weyl點,包括兩對II型的Weyl點和一對I型的Weyl點,其中最低頻率d帶與其他能帶交叉導致的Weyl點的三維色散由圖8給出.

圖8 由Dirac點衍生得到的Weyl點 (a)對稱性破缺的原胞結構,上圖為原胞結構放大的俯視圖,下圖為沿[110]方向的側視圖,幾何結構參數為b1=0.1,b2=0.11,b3=0.094,h1=0.5,h2=0.3;(b)kz方向上的光子能帶圖,對應的能帶交叉點就是Weyl點;(d)Weyl點的三維色散圖,上圖為II型的Weyl點,下圖為I型的Weyl點Fig.8.Weyl points derived from Dirac points:(a)Unit cell structure of the symmetry-broken,upper panel is 3D view with zoom in illustration of structure deformation,lower panel is side view from[110]direction,the geometry parameters are b1=0.1,b2=0.11,b3=0.094,h1=0.5,and h2=0.3,the z coordinates of the centers of the two types of dielectric blocks are 0 and 0.65a;(b)band structure of MA line for lowest six bands,the crossing points are Weyl points;(c)3D dispersion of Weyl points,upper panel is type-II Weyl point,lower panel is type-I Weyl point.

5 結 論

光子晶體中的Dirac點作為實現各種拓撲態的一種重要母態,對光子拓撲理論的研究具有重要的指導意義,如何在光子晶體中實現Dirac點無疑是光子拓撲理論中的一個核心研究課題.通常人們根據光特有的偏振特性來模擬電子系統中的自旋簡并態,然而這種方式往往受限于材料的特殊要求(通常只能在特殊頻率范圍實現,在光學和近紅外頻率范圍往往失效)而不具備普適性.本文介紹了利用包括非點群對稱性在內的晶格對稱性來實現Dirac光子晶體的方法,涵蓋了二維及三維光子晶體,實現了在高對稱點/高對稱線上的相對穩定的Dirac點.由于利用晶格對稱性的方法并不需要考慮研究對象的粒子屬性,可以預見這種方法具有很好的可移植性,包括拓撲聲子/彈性波系統在內的經典體系均可以通過這種方式來實現.由此可見,受對稱性保護的Dirac點在拓撲系統中的應用仍然值得人們深入研究.

[1]Dirac P A M 1928Proc.R.Soc.London A118 351

[2]Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009Rev.Mod.Phys.81 109

[3]Novoselov K S,Jiang Z,Zhang Y,Morozov S V,Stormer H L,Zeitler U,Maan J C,Boebinger G S,Kim P,Geim A K 2007Scinece315 1379

[4]Katsnelson M I,Novoselov K S,Geim A K 2006Nat.Phys.2 620

[5]Shen S Q 2012Topological Insulators:Dirac Equation in Condensed Matters(London,Berlin Heidelberg:Springer-Verlag)

[6]Haldane F D M 1988Phys.Rev.Lett.61 2015

[7]Kane C L,Mele E J 2005Phys.Rev.Lett.95 146802

[8]Kane C L,Mele E J 2005Phys.Rev.Lett.95 226801

[9]Fu L,Kane C L,Mele E J 2007Phys.Rev.Lett.98 106803

[10]Weyl H Z 1929Physik56 330

[11]Haldane F D M,Raghu S 2008Phys.Rev.Lett.100 013904

[12]Wang Z,Chong Y D,Joannopoulos J D,Soljacic M 2008Phys.Rev.Lett.100 013905

[13]Ao X Y,Lin Z F,Chan C T 2009Phys.Rev.B80 033105

[14]Khanikaev A B,Hossein M S,Tse W K,Kargarian M,MacDonald A H,Shvets G 2013Nat.Mater.12 233

[15]Ma T,Khanikaev A B,Hossein M S,Shvets G 2015Phys.Rev.Lett.114 127401

[16]Chen W J,Jiang S J,Chen X D,Zhu B C,Zhou L,Dong J W,Chen C T 2014Nat.Commun.5 5782

[17]He C,Sun X C,Liu X P,Lu M H,Chen Y L,Feng L,ChenY F 2016Proc.Natl.Acad.Sci.USA113 4924

[18]Wu L H,Hu X 2015Phys.Rev.Lett.114 223901

[19]Sabyaschi B,Hirokazu M,Wade D,Edo E,Mohammad H2016New J.Phys.18 113013

[20]Xu L,Wang H X,Xu Y D,Chen H Y,Jiang J H 2016Opt.Express24 18059

[21]Wang H X,Xu L,Chen H Y,Jiang J H 2016Phys.Rev.B93 235155

[22]Wang H X,Chen Y G,Hang Z H,Kee H Y,Jiang J H 2017npj Quantum Materials2 54

[23]Sakoda K 2004 Optical Properties of Photonic Crystals(Berlin:Spring)

[24]Sakoda K 2012Opt.Express20 25181

[25]Mcphedran R C,Nicorovici N A,Mckenzie D R,Botten L C,Parker A R,Rouse G W 2001Aust.J.Chem.54 241

[26]Sanders J V 1964Nature204 1151

[27]Bernevig B A,Hughes T L,Zhang S C 2006Science314 1757

[28]Lidorikis E,Sigalas M M,Economou E N,Soukoulis C M 1998Phys.Rev.Lett.81 1405

[29]Yang B J,Nagaosa N 2014Nat.Commun.5 4898

[30]Yang B J,Morimoto T,Furusaki A 2015Phys.Rev.B92 165120

[31]Lu L,Joannopoulos J D,Soljacic M 2013Nat.Photon.7 294

PACS:03.65.Vf,41.20.Jb,42.25.GyDOI:10.7498/aps.66.220302

*Project supported by the National Natural Science Foundation of China(Grant No.11675116)and the Fculty Startup Funding of Soochow University.

?Corresponding author.E-mail:xikeda20072862@163.com

?Corresponding author.E-mail:joejhjiang@hotmail.com

Dirac photonic crystal?

Wang Hai-Xiao1)?Xu Lin Jiang Jian-Hua1)2)?

1)(Department of Physics,Optoelectronics and Energy,Soochow University,Suzhou 215006,China)2)(Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,China)

15 August 2017;revised manuscript

31 October 2017)

Dirac Fermion,as one of the basic particles in the particle physics,nowadays have been widely used to describe the electronic states with the behavior of Dirac fermion in the topological electronics.These exotic electronic states are called Dirac point,which exhibited as a linear crossing point in the band structure.Usually Dirac point is the topological phase transition point and thus viewed as the mother state of various topological states.As an analogue of topological electronics,topological photonics,also attracted a great deal of interest due to its potential application.One of the key topic in topological photonics is to realize photonic bands with Dirac point.In this review,we brie fly introduce the progress of Dirac point in the photonic system and focus on the realization method of Dirac point in photonic crystal by take advantage of lattice symmetry.We also discuss Weyl point in the photonic crystal as an extension of the Dirac point.

photonic crystal,Dirac point,topological band,quantum spin Hall e ff ect

10.7498/aps.66.220302

?國家自然科學基金(批準號:11675116)和蘇州大學科研啟動基金資助的課題.

?通信作者.E-mail:xikeda20072862@163.com

?通信作者.E-mail:joejhjiang@hotmail.com