群遮效應對海上結構物波漂移力的低減作用

何廣華，張志剛，張子豪，張世軍

(哈爾濱工業大學(威海) 船舶與海洋工程學院，山東 威海 264209)

群遮效應對海上結構物波漂移力的低減作用

何廣華，張志剛，張子豪，張世軍

(哈爾濱工業大學(威海) 船舶與海洋工程學院，山東 威海 264209)

針對波浪作用下海上浮式建筑物的波漂移力問題，考慮在海上建筑物周圍合理地布設小型浮體群以降低海上建筑物的波漂移力。本文基于波浪交互理論和高階邊界元方法，建立了分析三維多浮體間群遮效應的數值模型。計算結果表明：通過優化外圍浮體的尺寸可以降低海上建筑物的波漂移力；本數值模型計入了浮體間的波浪相互干涉作用，對群遮效應的預報更加準確和接近工程實際問題。隨著入射波頻率的不同，發生群遮效應所對應的外圍浮體尺寸不同；群遮效應不僅可以降低所需防護海上建筑物的波漂移力，也可以降低整個浮體群的波漂移力。

群遮效應； 多浮體； 波浪交互理論； 高階邊界元方法； 波浪干涉； 波漂移力

在海洋資源和空間利用過程中，波浪荷載是海上浮式建筑物所受的主要荷載之一[1]。由于波漂移力等波浪載荷的作用，海上浮式建筑物經常需要進行錨泊定位，波漂移力等波浪荷載直接影響著錨鏈等系纜的安全性和經濟性[2]。目前人們主要關注：通過改變海上浮式建筑物的水動力特性，提高結構強度和安全系數等方式來確保建筑物的安全。但是，建筑物仍置于惡劣海洋環境中這一事實并沒有改變。本文基于一種全新的理念，通過在海上浮式建筑物周圍布設一種海洋工程裝備——浮體群(防護衣)，利用浮體群之間的群遮效應，從根本上降低波浪對海上浮式建筑物的作用。

cloaking的相關研究是近年非常新穎的國際前沿研究。cloaking最早是由Pendry等[3]在電磁波研究領域發現。cloaking是指沒有散射波向外輻射傳播的現象。隨后，這種現象被應用到其他領域中，Zigoneanu等在實驗的基礎上分別研究了聲波和地震波的cloaking現象[4-5]。水波領域cloaking現象的研究正處于初步發展階段，Alam通過在浮體外圍的水底安裝Ripples，將表面重力波激發為內波，從而實現了對水面浮體的保護[6]。Porter理論上驗證了改變海底地形，實現單圓柱浮體cloaking現象的可能性[7]。Newman通過在單圓柱浮體周圍布設一定數量的圓柱浮體研究了群遮效應下的cloaking現象[8]。計算結果表明:通過優化外圍圓柱的尺寸參數,中心圓柱的散射波能量可以減小到幾乎為0。

波浪交互理論最先由Ohkusu[9]應用于水波計算問題中，隨后Kagemoto等[10-11]進一步拓展了波浪交互理論在多浮體水動力計算中的應用。

本文中浮體群的布置方式與Newman[8]的相同。為了提高計算精度，基于Kashiwagi[12]的高階邊界元方法進行開發和模擬。浮體波漂移力采用Maruo[13]的遠場方法計算得到。基于波浪交互理論和高階邊界元法，本文計算了在不同外圍浮體數時的群遮效應下，中心浮體、外圍浮體以及整個浮體群的波漂移力。計算結果表明，群遮效應不僅可以降低中心浮體的波漂移力，而且可以降低整個浮體群的波漂移力。

1 數學模型及數值方法

1.1速度勢

數值模型以拉普拉斯方程為基本控制方程。假設流體不可壓縮并且無粘、無旋，這樣流場可以用速度勢表達。速度勢Φ(x,y,z;t)滿足線性邊界條件。

根據線性疊加定理，速度勢可以表達為

其中

φ(P)=φI(P)+ψ(P)

式中：ζI和ω表示入射波波幅和圓頻率，P(x,y,z)表示流場中的點，φ(P)為入射勢φI(P)與擾動勢ψ(P)之和。

入射勢可以在柱坐標系中表示為

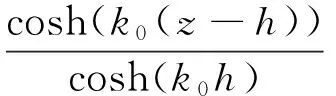
(1)

其中

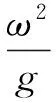
式中：β表示入射波與x軸的夾角，h表示有限水深。

Kagemoto等[10]詳細地介紹了波浪交互理論。這一理論，可充分考慮浮體群之間的波浪相互干涉作用。當外圍浮體數為N時，ψ(P)可以表示為

式中 Hm(2)表示m階的第二類漢克爾函數。

由Maruo[13]的遠場方法可知，浮體群外一定距離處速度勢的遠場表達式為

為進一步得到第n個浮體的速度勢，在第n個浮體上引入局部柱坐標系。此時第n個浮體的入射勢由式(1)給出的全局入射勢和其他浮體產生的擾動勢兩部分組成，因此總的速度勢可表示為

Z0(z)e-imθn

(2)

其中

1.2波漂移力

Kashiwagi等采用朗斯基矩陣推導出了波漂移力的表達式[14]。本文采用同樣的方法，利用式(2)可以得到第n個浮體的波漂移力：

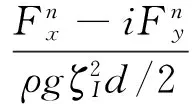
(3)

2 波漂移力數值模擬結果與分析

為了準確計及浮體間相互作用情況下的二階漂移力，本文采用了兩種坐標系，如圖1所示。一種是放置在中心浮體上的全局坐標系o-xyz，一種是放置在第n個浮體上的局部坐標系on-xnynzn。除了笛卡爾坐標系外，本文還采用了柱坐標系；z軸豎直向上，每一個坐標系的原點位于未擾動的自由表面(z=0)。

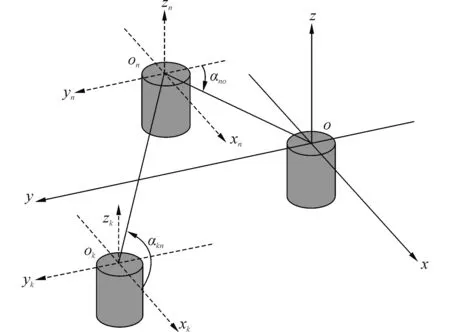
圖1 全局坐標系與局部坐標系的關系Fig.1 Global and local coordinate systems

2.1浮體群模型

Newman[8]研究了入射波數為K=1.0時，多浮體群遮效應下的散射波能量。

計算結果表明：通過優化外圍浮體的吃水、直徑以及外圍浮體與中心浮體的距離等參數，可以使浮體群的散射波能量減小到幾乎為0，即cloaking現象產生。對應的外圍浮體尺寸參數與散射波能量，如表1所示。

本文采用同Newman[8]相同的布置方式，入射波方向為x軸負方向，如圖2所示。多個圓柱(N=4,8,16)規律地環繞在中心圓柱的周圍，并構成一個同心圓。外圍圓柱尺寸相同且等間距分布，中心圓柱的半徑r=0.5，吃水d=1.0，如圖3所示。本文中波漂移力進行了無量綱化處理:F=2Fx/ρgζI2d，其中Fx為x方向的波漂移力，ρ為流體密度，g為重力加速度，ζI為入射波波幅，d為浮體吃水。表1中同時給出了本文關于所需保護浮體波漂移力的計算結果。

表1 外圍浮體尺寸參數的優化值

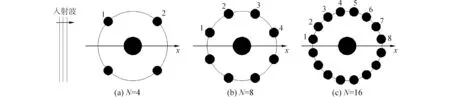
圖2 入射波方向與浮體編號(俯視圖)Fig.2 The direction of incident waves and notations (top view)

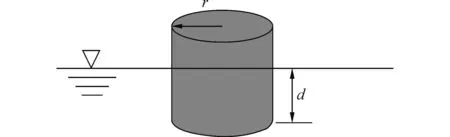
圖3 浮體形狀尺寸(浮體吃水與半徑)Fig.3 Geometrical dimensions of floating bodies(draft and radius of floating body)

圖4為表1中衰減系數與外圍浮體數N的關系。從圖4可以看出，隨著外圍浮體數的增多，散射波能量逐漸較小并趨近于0。本文針對需保護浮體的波漂移力計算結果(圖中F/F0)與散射波能量(圖中E/E0)的變化趨勢相同，驗證了群遮效應對波漂移力的低減作用。需要指出的是：在外圍浮體數N>8后，群遮效應對波漂移力的低減效果增加并不明顯，建議工程應用時，外圍浮體數不大于8即可。

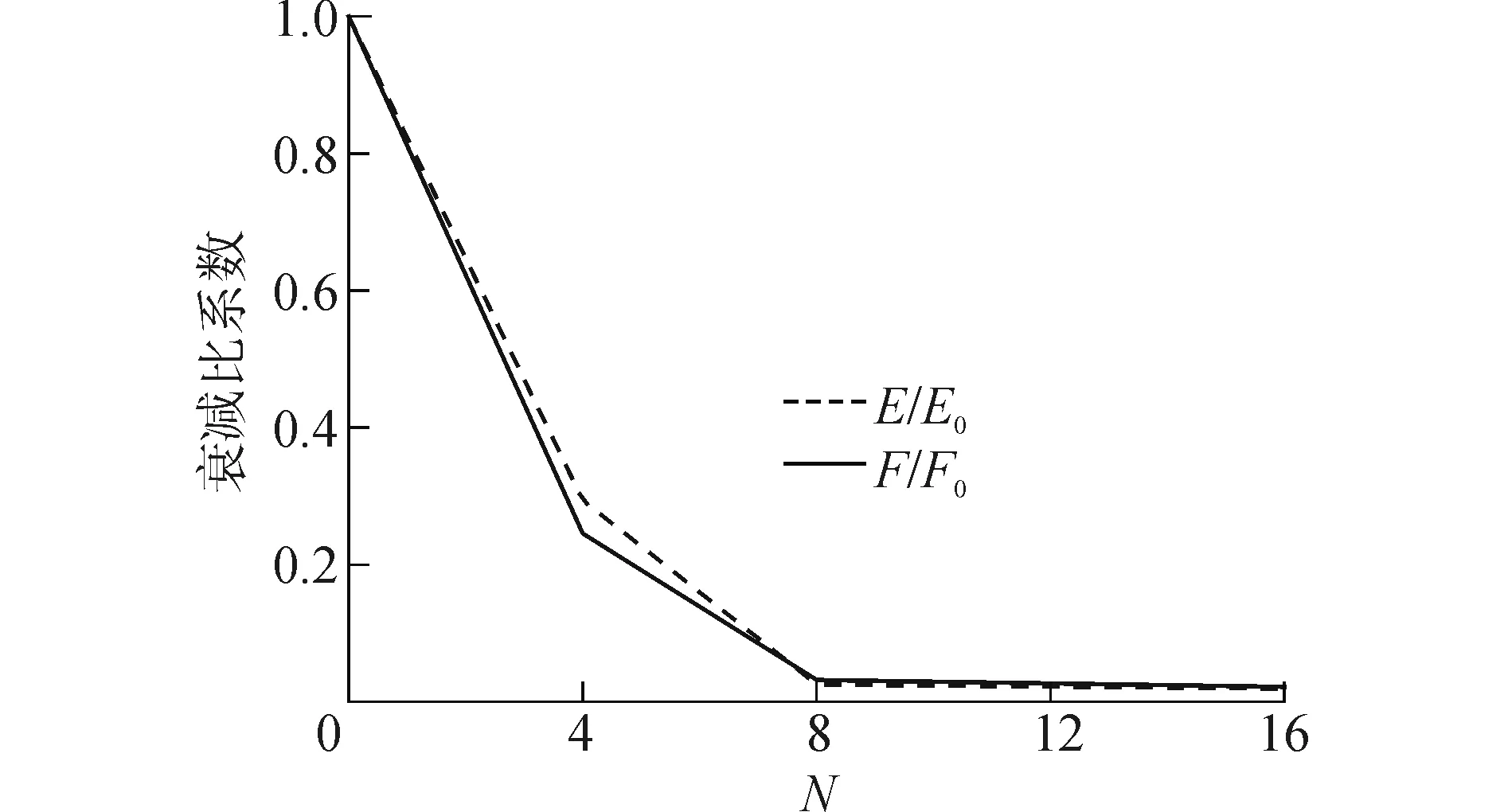
圖4 衰減系數與外圍浮體數N的關系Fig.4 The relationship between attenuation coefficient and the number of outer floating bodies

2.2波漂移力與波數的關系

本節采用表1中的外圍浮體尺寸參數，計算了波漂移力與入射波數K之間的關系。圖5給出了不同外圍浮體數(N=4, 8, 16)的中心浮體、浮體群以及外圍浮體的漂移力(合力)。

在圖5中可以看出孤立圓柱(N=0)的波漂移力隨著波數的增加而增加。圖5(a)是中心圓柱的波漂移力，可以發現在外圍布設圓柱浮體后，中心圓柱的波漂移力相比于單個圓柱發生了明顯的變化，這是因為多浮體之間產生了復雜的波浪相互干涉。在波數K=1.0時，中心圓柱的波漂移力相對于單個圓柱浮體的波漂移力明顯較小，顯示了群遮效應對波漂移力的低減作用；與Newman[8]關于散射波能量的研究結論一致，并且外圍浮體的數量越多，群遮效果越明顯。圖5(b)、(c)分別給出了對應的浮體群和外圍浮體的漂移力。可以看到，波漂移力在波數K=1.0時，幾乎同樣減小到0，這表明群遮效應不僅可以降低中心海上建筑物的波漂移力，也可以降低整個浮體群的波漂移力。

圖6給出了每個外圍浮體的波漂移力，由于浮體布設的對稱性，只需給出其中一半浮體結果即可(浮體編號如圖2所示)。從圖6(a)中可以看出，兩圓柱的波漂移力在K=1.0時，方向相反、大小近似；圖5(b)中1號圓柱與4號圓柱的的波漂移力方向相反、大小近似，2號和3號圓柱的波漂移力幾乎為0；圖5(c)中1號圓柱與8號圓柱、2號圓柱與7號圓柱、3號圓柱與6號圓柱的波漂移力在K=1.0時方向相反、大小近似，而4號圓柱與5號圓柱的波漂移力幾乎為0。這表明正是由于結構關于y軸的對稱性，才使得在群遮效應發生時整個浮體群的漂移力合力也減小到幾乎為0。還需要指出的是，迎浪側圓柱的波漂移力絕對值變化較大，特別是1號圓柱的變化最大；并且，由于波浪復雜相互干涉作用，在某些波數范圍內迎浪側的圓柱波漂移力變為負值(與入射波方向相反)。

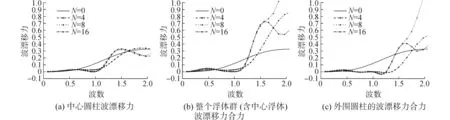
圖5 漂移力與入射波數的關系Fig.5 The relationship between wave drift force and wavenumber

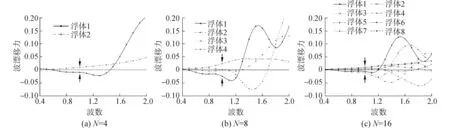
圖6 外圍單個圓柱的波漂移力Fig.6 The wave drift force on every outer cylinder

2.3波漂移力與外圍浮體數N的關系

本文中的外圍圓柱浮體的尺寸參數采用的是Newman[8]在波數K=1.0時以散射波能量為目標函數的優化結果，如表1所示。本節在計算波數K=1.0情況下不同外圍浮體數(N=4, 8, 16)的波漂移力之外，采用同樣的外圍圓柱尺寸還給出了其他波數(K=0.1, 0.5, 1.5, 2.0)下的波漂移力，計算結果如圖7所示。

從圖7中可以看出，在波數K=1.0時，中心圓柱的波漂移力與浮體群的波漂移力合力都隨著外圍浮體數的增加而減小，而在其他波數則不存在這樣的規律。說明針對不同的入射波頻率，特別是大波數情況，需要分別優化外圍浮體的尺寸參數才能實現多浮體的群遮效應。

圖7 波漂移力與外圍浮體數N的關系Fig.7 The relationship between wave drift force and the number of outer cylinders

2.4本文方法與Fang等提出的方法的對比

對于多浮體波漂移力的計算，Fang等[15]提出了一種忽略浮體間相互干涉效應的簡便計算方法。針對中心浮體波漂移力，本節給出了本文方法與Fang等[15]方法的對比結果，如圖8所示。

圖8(a)為孤立圓柱時的波漂移力，本文計算結果與Fang等[15]計算結果一致。圖8(b)、(c)中兩種方法的計算結果出現了差異，特別是在波數K=1.0附近。群遮效應是由于波浪復雜

相互干涉作用即產生的，Fang等[15]的方法因忽略了波浪的相互干涉，而在波數K=1.0(即群遮效應最顯著點)，計算結果誤差較大。此外，在小波數(長波)范圍內，Fang等[15]的方法與本方法的計算結果吻合較好，這是因為小波數情況下，波浪的相互干涉作用并不明顯，可以忽略。但是在大波數情況下，浮體間的波浪干涉作用更加復雜，此時不可以忽略波浪干涉對浮體波漂移力的影響。

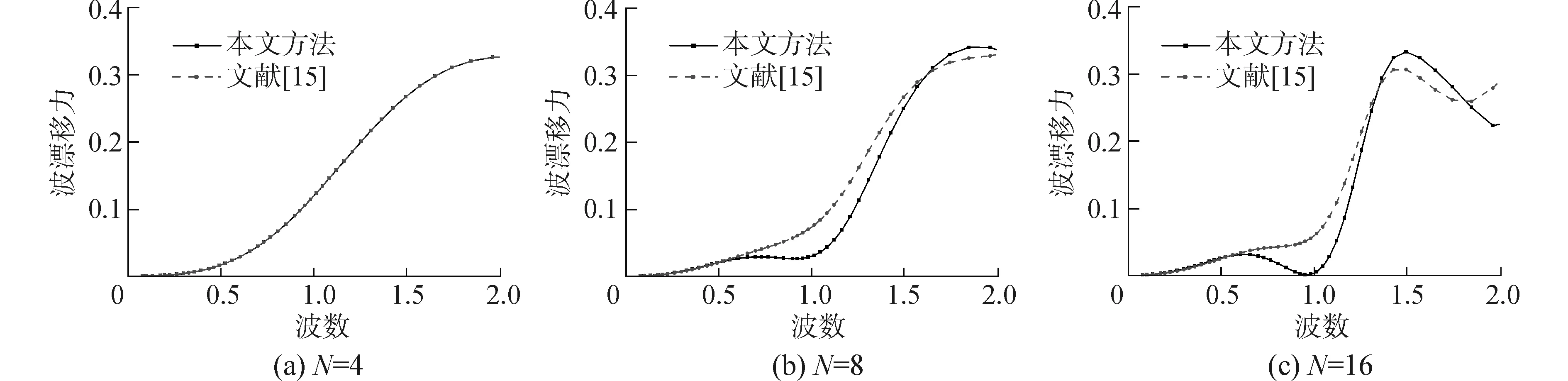
圖8 本文計算方法與Fang等[15]的計算方法的對比(中心圓柱波漂移力)Fig.8 Comparison of wave drift forces between Fang′s results[15] and the present solution

3 結論

1)群遮效應不僅可以降低中心海上建筑物的波漂移力，也可以降低整個浮體群的波漂移力。

2)在目標波數下(K=1.0)，中心浮體的波漂移力隨著外圍浮體數的增多而單調遞減并逐漸趨于0。

3)不同入射波頻率，發生群遮效應所對應的外圍浮體尺寸不同。

4)本文建立的數值模型計及了浮體間的波浪相互干涉作用，對群遮效應的預報更加準確。

[1] 桂琴琴, 鄒志利, 王大國. 箱型船體波浪和波浪壓力的非線性時域模型[J]. 工程力學, 2011, 28(2): 239-245.

GUI Qinqin, ZOU Zhili, WANG Daguo. Time-domian model of nonlinear wave forces on a box-shaped ship [J]. Engineering mechanics, 2011, 28(2): 239-245.

[2] 繆泉明, 顧民, 楊占明, 等. 極限海況下浮標運動及錨鏈受力估算[J]. 船舶力學, 2003, 7(5): 21-27.

MIU Quanming, GU Min, YANG Zhanming, et al. Estimation of buoy motions and chain forces in extreme sea state [J]. Journal of ship mechanics, 2003, 7(5): 21-27.

[3] PENDRY J B, SCHURIG D, SMITH D R. Controlling electromagnetic filed[J]. Science, 2006, 312: 1780-1782.

[4] ZIGONEANU L, POPA B, CUMMER S A. Three-dimensional broadband omnidirectional acoustic ground cloak[J]. Nature materials, 2014, 13(4): 352-355.

[5] BRULE S, JAVELAUD E H, ENOCH S， et al. Experiments on seismic metamaterials: molding surface waves[J]. Physical review letters, 2014, 112(13): 133901.

[6] ALAM M. Broadband cloaking in stratified seas[J]. Physical review letters, 2011, 108: 1-5.

[7] PORTER R. Cloaking of a cylinder in waves[C]//26thInternational Workshop on Water Waves and Floating Bodies, Greece, 2011, 36: 1-4.

[8] NEWMAN J N. Cloaking a circular cylinder in deep water[C]//28thInternational Workshop on Water Waves and Floating Bodies, L′isle surla Sorgue, France, 2013: 157-160.

[9] OHKUSU M. Hydrodynamic forces on multiple cylinders in waves[C]//The Process of International Symposium Dynamics of Marine Vehicles and Structures in Waves, London, 1974: 261-268.

[10] KAGENOTO H, YUE D K P. Three-dimensional bodies in water waves: an exact algebraic method[J]. Journal of fluid mechanics, 1986, 166: 189-209.

[11] LINTON C M, EVANS D V. The interaction of waves with arrays of cylinders[J]. Journal of fluid mechanics, 1990, 215: 549-569.

[12] KASHIWAGI M. 3-D calculation for multiple floating bodies in proximity using wave interaction theory[J]. Journal of offshore and polar engineering, 2008, 18: 1-7.

[13] MARUO H. The drift of a body floating on waves[J]. Journal of ship research, 1960, 4: 1-10.

[14] KASHIWAGI M, YOSHIDA S. Wave drift force and moment on a VLFS supported by a great number of floating columns[J]. International journal of offshore and polar engineering, 2001, 11: 176-183.

[15] FANG M C, CHEN G R. On three-dimension solution of drift forces and moments between two ships in waves[J]. Journal of ship research, 2002, 46(4): 280-28.

本文引用格式：

何廣華，張志剛，張子豪，等. 群遮效應對海上結構物波漂移力的低減作用[J]. 哈爾濱工程大學學報， 2017， 38(11): 1676-1681.

HE Guanghua, ZHANG Zhigang, ZHANG Zihao, et al. Reduction in wave drift force on marine structures by cloaking phenomenon[J]. Journal of Harbin Engineering University， 2017， 38(11): 1676-1681.

Reductioninwavedriftforceonmarinestructures
bycloakingphenomenon

HE Guanghua, ZHANG Zhigang, ZHANG Zihao, ZHANG Shijun

(School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology, Weihai 264209, China)

This study aims to examine the reduction in the wave drift force acting on a floating structure, such as an offshore platform, by appropriate positioning of small floating bodies around the floating structure. To investigate the cloaking phenomenon on 3D multiple floating bodies, a numerical model using a combination of wave interaction theory and the higher-order boundary element method is introduced. Computed results show that reduction in the wave drift force on the offshore structure is realized using optimized parameters of the surrounding floating bodies. Numerical computations were highly accurate and benefited from considering the interactions between multi-bodies, and the optimized parameters of the surrounding bodies were different in relation to the various wave frequencies. Results show that the cloaking phenomenon can reduce the wave drift force on the central structure and on the entire array of floating bodies.

cloaking phenomenon; multiple floating bodies; wave interaction theory; higher-order boundary element method; wave interactions; wave drift force

10.11990/jheu.201607009

http://www.cnki.net/kcms/detail/23.1390.u.20171016.1546.004.html

U661.1

A

1006-7043(2017)11-1676-06

2016-07-04.

網絡出版日期：2017-10-16.

國家自然科學基金項目(11502059); 大連理工大學海岸和近海工程國家重點實驗室開放課題基金項目(LP1513); 哈爾濱工業大學科研創新項目(HIT.NSRIF.201726); 水沙科學與水災害防治湖南省重點實驗室基金(2015SS02); 衛星海洋環境動力學國家重點實驗室(國家海洋局第二海洋研究所)項目(SOED1514).

何廣華(1980-), 男, 教授, 博士生導師；

張志剛(1992-), 男, 碩士研究生.

何廣華, E-mail: ghhe@hitwh.edu.cn.