季節性冰凍河流航電樞紐施工優化

李明偉，王劍倫,2，耿敬，劉峰，陳志遠

(1.哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001; 2.黑龍江中北航務勘察設計有限公司，黑龍江 哈爾濱 150001)

季節性冰凍河流航電樞紐施工優化

李明偉1，王劍倫1,2，耿敬1，劉峰1，陳志遠1

(1.哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001; 2.黑龍江中北航務勘察設計有限公司，黑龍江 哈爾濱 150001)

為提高航電樞紐工程施工效率，本文以施工工期最短為優化目標，計入冰凍對航電樞紐施工的影響，以施工強度與機械設備為約束條件，提出了季節性冰凍河流航電樞紐施工進度優化模型(SO-NPJC)。基于蝙蝠算法、混沌、小生境理論，提出混沌小生境蝙蝠優化算法(CNBA)。構建面向季節性冰凍河流航電樞紐施工的SO-NPJC-CNBA優化模型。結合依蘭航電樞紐工程開展數值實驗，結果表明：本文建立的SO-NPJC-CNBA優化模型在解決航電樞紐工程施工優化問題上提升了航電樞紐的建造效率，縮短了施工工期，為實現樞紐的智慧建造提供了技術支持，體現了優化模型的可行性和優越性。

航電樞紐； 冰凍河流； 施工優化； 蝙蝠算法； 混沌理論； 小生境理論

季節性冰凍河流中江水易結冰、水文情勢多變、低溫與流冰會給航電樞紐金屬結構與建筑物帶來諸多不利的影響，冰凍期混凝土的澆筑會直接影響樞紐建設，甚至可能造成水電工程事故、建筑物損壞等 在針對航電樞紐的施工中，可能存在施工期內雨季多發，導致施工期變短。此外，由于施工作業面狹窄，勢必導致互相干擾，這也將給施工過程中的工期、質量等控制帶來更多不確定因素，加大了施工管理的難度。因此良好的施工進度管理是工程如期完工的重要保證。

目前，國內外學者對施工進度優化模型進行了廣泛的研究，但其在實際應用中存在較大誤差。基于不同關注點建立施工優化模型后，對優化模型的求解是獲得較優方案的關鍵[1-2]。蝙蝠算法(bat algorithm，BA)是近年來發展起來的一種新興演化計算技術[3]，具有易于實現、收斂速度快、適于并行處理、魯棒性強等特點[4]。但與其他仿生群智能算法類似，標準BA也存在易陷入局部最優、過早收斂、后期收斂速度較慢等問題。綜上，目前雖然已經有許多文獻對施工進度優化方法進行了研究，但是均存在諸多不足，同時未見關于面向季節性冰凍河流航電樞紐施工工期優化研究的報道。

本文考慮到航電樞紐工程施工的經濟費用比較固定，計入冰凍因素對施工進度的影響，建立以施工強度與機械設備為約束條件的施工進度優化模型[5]。為了更好的求解建立的施工進度優化模型(schedule optimization model for navigation-power junction construction of seasonal frozen river，SO-NPJC)，基于混沌映射和小生境理論，對BA進行改進，提出了混沌小生境蝙蝠算法(chaos niche bat algorithm，CNBA)。建立了一種基于CNBA的季節性冰凍河流航電樞紐施工進度優化方法。最后結合依蘭航電樞紐工程實例，進行數值實驗，通過對實驗結果的對比分析，驗證了新建優化方法的實用性與優越性。

1 施工進度優化模型的建立

本文建立的航電樞紐工程施工進度優化模型基于以下假設條件：1)不考慮工程各項工序的施工銜接時間；2)當連續5 d平均氣溫降到5 ℃，或最低氣溫降到0 ℃，工程進入冬季施工期，混凝土停止澆筑；3)關鍵線路的持續時間為工程的總工期；4)單項工程的施工強度、機械設備數目與其工期呈線性相關。綜合考慮工程中混凝土的實際澆筑情況與冰凍因素對施工的影響，以施工強度與施工機械設備為約束條件，以施工總工期最短為優化目標，建立SO-NPJC優化模型如下

(1)

(2)

式中：D為影響工程總工期的工序數目,xi為單項工程實際工期,x0i為單項工程計劃工期,Fi為單項工程計劃施工強度,Fi min為實際情況下單項工程最小施工強度,Fi max為實際情況下單項工程最大施工強度,γ為施工強度增大系數,α為設備資源的增加百分比,T為工程總工期。

2 蝙蝠優化算法

2.1標準蝙蝠算法的優化機理

BA由英國學者X. S. Yang[6]受到了蝙蝠捕獵過程中回聲定位行為的啟發，于2010年提出的。在捕獵過程中，蝙蝠首先發出一種聲音信號，信號在碰到獵物時被彈回，蝙蝠通過分析回聲的頻率、響度和脈沖發射率等特征，來確定物體的性質和位置。

2.1.1 蝙蝠的速度和位置更新過程

Fi=Fmin+(Fmax-Fmin)β

(3)

(4)

(5)

式中：Fi、Fmax和Fmin為第i只蝙蝠在當前時刻發出的聲波頻率、聲波頻率的最大值和最小值；β為隨機數，β∈[0,1]；x*為當前最優解。

對于大小為N的蝙蝠群體，可以從中選擇一只蝙蝠(解)，并更新該蝙蝠相應的位置，即在被選擇解的附近產生一個新解：

(6)

該過程可被理解為局部搜索過程。式中：xold為從當前最優解集中隨機選擇的一個解，At為當前代前i只蝙蝠的平均響度；ε為隨機變量，ε∈[0,1]D。

2.1.2 響度和脈沖發射率

蝙蝠實際捕獵過程中，其聲波響度A(i)隨著與獵物距離的減小而不斷減弱，但脈沖發射速率R(i)隨著與獵物距離的減小而逐漸提高。蝙蝠i脈沖的響度A(i)和發射速率R(i)可更新為

At+1(i)=αAt(i)

(7)

Rt+1(i)=R0(i)[1-exp(-γt)]

(8)

式中：0<α<1和γ>0均為常量;A(i)=0時意味著蝙蝠i剛剛發現一只獵物，暫時停止發出任何聲音。

2.2混沌小生境蝙蝠優化算法

混沌算法是一種新穎的優化技術，在工程實踐中得到了廣泛的應用。在數值問題的優化方面，利用混沌算法在求解時，將搜索過程中產生的解通過混沌映射方程映射到變量空間中，利用混沌變量的遍歷性、隨機性的特點尋找最優解，從而可以在搜索過程中避免陷入極小值，最終獲得全局最優解[7]。針對混沌算法的隨機性、有界性等特點，很多文獻基于混沌映射建立了改進算法[7-8]。

本文針對BA的不足，為了增強BA種群的多樣性，提高算法后期的搜索速度，嘗試將混沌理論用于BA的改進。針對種群多樣性下降，本文利用Tent映射，設計混沌遍歷搜索機制和小生境局部搜索機制，以期能夠較快地求出所求問題的最優解或滿意解，提高算法全局和局部搜索能力[9]。Tent映射方程如下

(9)

2.2.1 混沌遍歷搜索機制(CTSM)

基于Tent映射的BA混沌遍歷搜索機制(chaos traversal search mechanism，CTSM)原理為：首先將蝙蝠個體映射到(0，1)范圍內，將映射后的個體作為初始值，利用Tent映射產生一定數目的混沌變量，然后將生成的混沌變量再映射到原來的解空間，獲得新的蝙蝠個體，評價生成的新個體，更新混沌遍歷搜索后的蝙蝠位置[10]。基于Tent映射的BA全局混沌遍歷搜索機制流程如下：

1)i=1，j=1，轉到步驟2)；

2)利用式(10)，將位于D維解空間中第i個蝙蝠個體j維分量，映射到區間(0,1)；

(10)

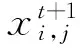
(11)

5)令j=j+1，轉到步驟7)；

6)如果j>D，轉到步驟8)，否則轉到步驟3)；

7)獲得m個混沌全局搜索后的蝙蝠個體；

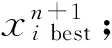
10)i=i+1；

11)如果i>N，轉到步驟13)，否則轉到步驟2)；

12)完成N個蝙蝠的全局混沌搜索。

2.2.2 小生境局部搜索機制(NLSM)

基于Tent映射的小生境局部搜索機制(niche local search mechanism，NLSM)原理為：首先從最優解集中選取最優解x*t，確定小生境局部搜索中心，將最優蝙蝠個體x*t的各維分量映射到區間(0，1)，將映射獲得的變量作為Tent映射的迭代初值，獲得迭代后混沌序列，計算小生境局部搜索半徑，確定小生境局部搜索范圍，將獲得迭代后的混沌序列映射到小生境局部搜索范圍內，進行小生境局部遍歷搜索，更新最優解x*t、脈沖響度At+1(i)和脈沖發射頻率Rt+1(i)[11]。

在進行小生境局部搜索過程中，首先定義小生境的中心和搜索半徑。設小生境局部搜索中心為當前被選的種群最優個體x*t，小生境局部搜索半徑r按下式確定：

r=min(x*t-aj,bj-x*t)

(12)

式中：r為小生境搜索半徑，bj、aj分別是蝙蝠第j維分量的最大值和最小值。小生境局部搜索機制流程如下：

2)j=1，轉到步驟3)；

3)利用式(13)，將最優蝙蝠個體x*t的第j維分量映射到區間(0,1)；

(13)

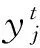
(14)

6)令j=j+1，轉到步驟7)；

7)如果j>D，轉到步驟8)，否則轉到步驟3)；

8)獲得m個在小生境內混沌全局搜索后的蝙蝠個體；

將機電一體化技術應用到工程機械設備中，通過該技術的信息控制系統，可對機械的作業過程進行自動化控制，如此一來，極大地提高了作業的精準度。例如，將機電一體化技術應用到瀝青的攤鋪機中，就可以實現自動找平、自動供料，不僅提高了施工的質量，也提高了施工的效率。可以說，通過機電一體化技術的應用，基本上實現了工程機械的半自動化 操作，進一步降低了人工操作中出現的誤差現象，提高了施工作業的精準度，滿足了現代工程施工的要求[3]。

2.2.3 CNBA的進化流程設計

針對蝙蝠算法的不足，基于Tent映射，設計用于改進蝙蝠算法的混沌遍歷搜索機制、小生境局部搜索機制，提出混沌小生境蝙蝠算法。CNBA的進化原理為：按照標準BA，初始化種群各蝙蝠的位置和速度，評價個體適應度值；若種群符合CTSM執行條件，按照CTSM進化流程，對種群執行混沌遍歷搜索機制；若種群符合NLSM執行條件，按照NLSM進化流程，對被選擇的較優個體執行小生境局部搜索機制；更新種群位置，繼續執行BA基本進化流程，直到滿足進化終止準則，結束進化。CNBA的進化流程如圖1。

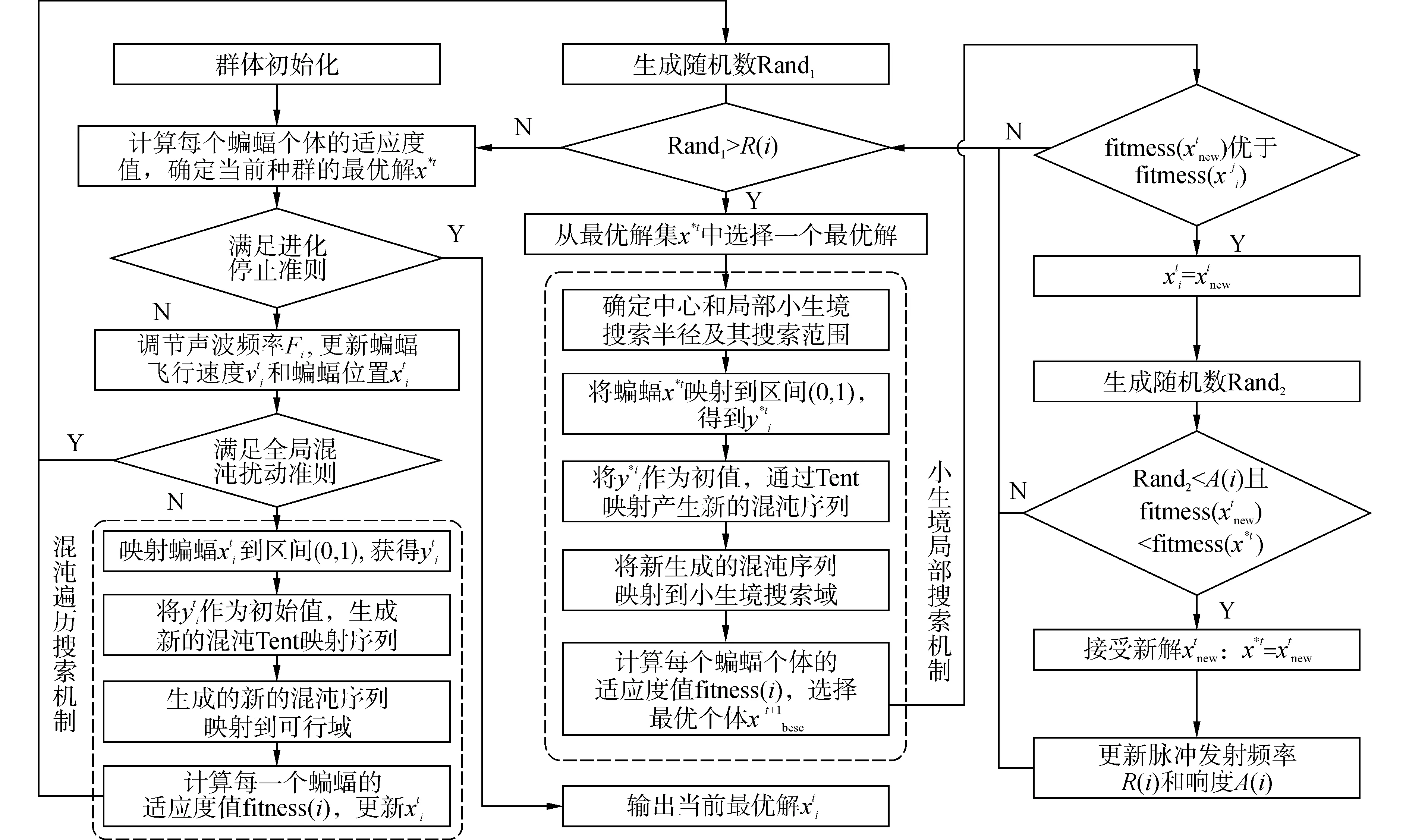
圖1 CNBA的進化流程Fig.1 The evolutionary processes of CNBA

3 基于CNBA算法對SO-NPJC求解

在施工進度優化模型求解過程中，根據最優解問題特點，將種群中蝙蝠個體的和作為適應度函數：

(15)

式中：D是影響工程總工期的工序數目,xi為單項工程實際工期。模型求解流程如下：

1)參數初始化。設置種群大小N，最大的迭代次數MaxIter，蝙蝠i的初始響度A(i)，脈沖發射速率R(i)，脈沖頻率的最大值fmax和最小值fmin，脈沖音強衰減系數α，脈沖頻度增加系數γ；

2)種群初始化。在蝙蝠可行域內(a，b)，隨機初始化蝙蝠位置xi和速度vi；

3)適應度評價。以每個蝙蝠的各維向量作為每項工序的實際工期，然后按照式(15)，計算第i個蝙蝠對應的適應度值fitness(i)；按照適應度值進行排序，選擇適應度值最小的個體作為當前種群最優個體x*t；

4)進化終止判斷。如果當前種群滿足進化終止條件，轉到步驟12，否則，轉到步驟5)；

5)更新脈沖頻率Fi。按照式(8)更新脈沖頻率，轉到步驟6)；

7)混沌遍歷搜索機制。如果當前種群滿足CTSM的執行條件，按照CTSM流程進行混沌遍歷搜索，轉到步驟8)；

8)小生境局部搜索機制。如果當前種群符合NLSM搜索條件，按照NLSM執行小生境局部搜索，轉到步驟9)；

11)按照式(7)、(8)，更新脈沖響度A(i)和脈沖發射率R(i)，然后轉到步驟3)；

12)輸出當前數據的最優解x*t。

4 實例應用

4.1工程概況

依蘭航電樞紐工程任務主要是以航運、發電為主，兼顧交通、灌溉和旅游等綜合利用功能。選取進行數值實驗工程的關鍵線路共11項工序，分別為：1)場內交通公路修建，計劃工期153 d；2)一期右岸戧堤砂礫石填筑，計劃工期45 d；3)一期右岸高噴灌漿，計劃工期46 d；4)一期右岸基坑排水，計劃工期31 d；5)廠房土方開挖，計劃工期31 d；6)廠房石方開挖，計劃工期73 d；7)一期廠房水下混凝土澆筑，計劃工期200 d；8)二期廠房水下混凝土澆筑，計劃工期47 d；9)廠房水上混凝土澆筑，計劃工期122 d；10)橋機安裝，計劃工期92 d；11)水輪機及發電機安裝，計劃工期731 d。此時建立的SO-NPJC模型具體表示如下

(16)

(17)

式中：γ=0.2；α=0.2。式(16)表示僅在工序2、3、5、6、7、8、9時考慮施工強度對工程工期的影響，僅在工序2、5、6時考慮施工機械設備對工程工期影響。

4.2模型選取及算法參數設置

本文分別應用PSO、BA、CTSM-BA、NLSM-BA、CNBA對建立的SO-NPJC模型進行求解。考慮到算法中涉及各參數的確定目前尚無確切的理論依據，本文根據反復實驗獲得的經驗值選擇各算法的最佳參數進行計算。PSO中：學習因子c1=c2=1.3，慣性權重w=0.3；BA中：搜索脈沖頻率范圍ri∈[-1,1]，最大脈沖頻度r0=0.75，最大脈沖音強A=0.25，脈沖音強衰減系數α=0.95，脈沖頻度增加系數γ=0.05；CTSM-BA中：基于Tent映射混沌遍歷搜索的迭代次數m=50，其余參數同BA；NLSM-BA中：小生境局部搜索半徑r=2，其余參數同BA；CNBA中：基于Tent映射混沌遍歷搜索的迭代次數m=50，小生境局部搜索半徑r=2，其余參數同BA。上述五種算法最大迭代次數均為Tmax=200，種群規模均取50。

4.3施工優化模型性能分析

考慮到進化算法的隨機性，為了保證檢驗過程的可靠性，本文在測試過程中，分別用五種算法對優化模型獨立求解30次，將30次求解結果平均后再輸出。各算法工期優化結果如表1。

表1 五種算法工期優化結果對比

由表1分析可知：PSO平均優化百分比為4.01%，對總工期優化了2.27%，優化后總工期與計劃相比縮短了36 d；BA平均優化百分比為4.57%，對總工期優化了2.21%，優化后總工期與計劃相比縮短了35 d；CTSM-BA平均優化百分比為7.62%，對總工期優化了3.64%，優化后總工期與計劃相比縮短了57 d，較BA提高了1.43%；NLSM-BA平均優化百分比為6.86%，對總工期優化了2.99%，優化后總工期與計劃相比縮短了47 d，較BA提高了0.78%；CNBA平均優化百分比為8.06%，對總工期優化了4.68%，優化后總工期與計劃相比縮短了74 d，較BA提高了2.47%，較PSO提高了2.41%。分析結果表明：本文提出的新算法計算所得結果波動相對較小，對工期優化幅度較大，應用于實際工程管理，可有效縮短工程施工總工期。

4.4優化算法性能分析

為了進一步測試新提出的CNBA算法在求解施工優化模型過程中的可行性，本文在測試過程中，同樣應用每種算法對模型分別獨立求解30次，計算適應度值的平均值，繪制適應度值平均進化曲線。五種算法平均收斂曲線如圖2。

由圖2可知，五種算法均取得了最優解，但PSO計算所得適應度值偏大，最后在迭代到第12代時收斂于1 535 d；BA計算所得適應度值與PSO近似，最后在迭代到第10代時收斂于1 536 d；CTSM-BA更好的遍歷了所有解，最后在迭代到第22代時收斂于1 514 d；NLSM-BA加快了解的收斂速度，最后在迭代到第9代時收斂于1 524 d。可以看出NLSM-BA較CTSM-BA收斂速度得到了提升，但CTSM-BA的解更加優秀；CNBA綜合了CTSM-BA和NLSM-BA的優點，即遍歷了所有優秀解又加快了算法的收斂速度，最后在迭代到第5代時收斂于1 497 d，工程原計劃總工期縮短了74 d。

圖2 航電樞紐工程總工期收斂曲線Fig.2 The convergence curves of total time limit for a navigation-power junction project

5 結論

1)應用五種智能優化算法分別對施工進度優化模型進行求解，均對關鍵線路上所有工序工期進行了優化，得到了工期最優解。

2)CNBA算法在優化求解的魯棒性、優化幅度等方面均優于PSO、BA、CTSM-BA、NLSM-BA算法，表現出了新算法較強的全局尋優能力和更高的搜索精度，證明了新算法的優越性。

3)將本文提出的施工優化方法應用于季節性冰凍河流航電樞紐工程施工，提升了航電樞紐的建造效率，縮短了施工工期，為實現樞紐的智慧建造提供了技術支持。

[1] 王卓甫, 陳登星. 水利水電施工進度計劃的風險分析[J]. 河海大學學報：自然科學版, 1999, 27(4): 83-87.

WANG Zhuofu, CHEN Dengxing. Risk analysis of construction schedule for water resource projects[J]. Journal of Hohai University, 1999, 27(4): 83-87.

[2] 劉明, 吳喚群. 資源有限—工期最短的分枝定界算法[J]. 系統工程, 1999(2): 72-75.

LIU Ming, WU Huanqun. A branch and bound method for problem of limited resources and shortest time limit for a project[J]. Systems engineering, 1999(2): 72-75.

[3] YANG X S. A new metaheuristic bat-inspired algorithm[J]. Computer knowledge & technology, 2010, 284: 65-74.

[4] 彭喜元, 彭宇, 戴毓豐. 群智能理論及應用[J]. 電子學報, 2003, 31(s1): 1982-1988.

PENG Xiyuan, PENG Yu, DAI Yufeng. Swarm intelligence theory and applications[J]. Acta electronica sinica, 2003, 31(s1): 1982-1988.

[5] 周樹發, 劉莉. 工程網絡計劃中的多目標優化問題[J]. 華東交通大學學報, 2004(2): 10-13.

ZHOU Shufa, LIU Li. The multi-goal optimization problem in network project[J]. Journal of East China Jiaotong University, 2004(2): 10-13.

[6] 康琦, 汪鐳, 吳啟迪. 群體智能與人工生命[J]. 模式識別與人工智能, 2005, 18(6): 689-697.

KANG Qi, WANG Lei, WU Qidi. Swarm intelligence and artificial life[J]. Pattern recognition & artificial intelligence, 2005, 18(6): 689-697.

[7] 劉長平, 葉春明. 具有混沌搜索策略的蝙蝠優化算法及性能仿真[J]. 系統仿真學報, 2013, 25(06): 1183-1188.

LIU Changping, YE Chunming. Bat algorithm with chaotic search strategy and analysis of its property[J]. Journal of system simulation, 2013, 25(06): 1183-1182.

[8] 王翔, 李志勇, 許國藝,等. 基于混沌局部搜索算子的人工蜂群算法[J]. 計算機應用, 2012, 32(4): 1033-1036.

WANG Xiang, LI Zhiyong, XU Guoyi, et al. Artificial bee colony algorithm based on chaos local search operator[J]. Journal of computer applications, 2012, 32(4): 1033-1036.

[9] 趙欣. 不同一維混沌映射的優化性能比較研究[J]. 計算機應用研究, 2012, 29(03): 913-915.

ZHAO Xin. Research on optimization performance comparison of different one-dimensional chaotic maps[J]. Application research of computers, 2012, 29(3): 913-915.

[10] 單梁, 強浩, 李軍,等. 基于Tent映射的混沌優化算法[J]. 控制與決策, 2005, 20(2): 179-182.

SHAN Liang, QIANG Hao, LI Jun, et al. Chaotic optimization algorithm based on tent map[J]. Control & decision, 2005, 20(2): 179-182.

[11] 高珊, 馬良, 張惠珍, 等. 函數優化的小生境蝙蝠算法[J]. 數學的實踐與認識, 2014(15): 253-260.

GAO Shan, MA Liang, ZHANG Huizhen, et al. Niche bat algorithm for function optimization[J]. Mathematics in practice & theory, 2014(15): 253-260.

本文引用格式：

李明偉，王劍倫，耿敬，等. 季節性冰凍河流航電樞紐施工優化[J]. 哈爾濱工程大學學報， 2017， 38(11): 1696-1701.

LI Mingwei, WANG Jianlun, GENG Jing, et al. Construction optimization of seasonal frozen rivers navigation-hydropower junction[J]. Journal of Harbin Engineering University， 2017， 38(11): 1696-1701.

Constructionoptimizationofseasonalfrozenriversnavigation-hydropowerjunction

LI Mingwei1, WANG Jianlun1,2, GENG Jing1, LIU Feng1, CHEN Zhiyuan1

(1.College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China; 2.Heilongjiang ZhongBei Harbor Consultans, Co.,Ltd, Harbin 150001, China)

In order to improve the efficiency of navigation-hydropower junction project construction, taking the shortest construction time as optimization objectives, and considering the influence of freezing on navigation-hydropower junction construction, this paper proposed the schedule optimization model for navigation-hydropower junction construction of seasonal frozen river (SO-NPJC), with the construction intensity and mechanical equipment as constraint conditions. Based on the bat algorithm, the chaotic and niche theory, the Chaos Niche Bat Algorithm (CNBA) was proposed and the SO-NPJC-CNBA optimization model was constructed for navigation-hydropower junction construction facing the seasonal frozen river. The numerical experiment was carried out by combination with Yilan navigation-hydropower junction project. The results show that, the SO-NPJC-CNBA optimization model established in this paper for solving the construction optimization problems of the navigation-hydropower junction project improves the efficiency of the navigation-hydropower junction construction, shortens the construction period, and provides technical support for realizing the intelligent water conservancy, showing the feasibility and superiority of the optimization model.

navigation hydropower junction; frozen rivers; construction optimization; bat algorithm; chaotic theory; niche theory

10.11990/jheu.201608064

http://www.cnki.net/kcms/detail/23.1390.u.20170427.1321.014.html

U615.1

A

1006-7043(2017)11-1696-06

2016-08-30.

網絡出版日期：2017-04-27.

國家自然科學基金項目(51509056)；交通運輸部信息化技術研究項目(2014364554050)；中國博士后科學基金面上項目(2015M571394).

李明偉(1984-), 男, 講師,博士；

耿敬(1968-), 女, 教授.

耿敬, E-mail: gengjing@hrbeu.edu.cn.