基于鏈?zhǔn)椒▌t的平面應(yīng)變梯度的計(jì)算分析★

呂 娜 殷玉沉 孫玉周

(中原工學(xué)院建筑工程學(xué)院，河南 鄭州 450007)

·結(jié)構(gòu)·抗震·

基于鏈?zhǔn)椒▌t的平面應(yīng)變梯度的計(jì)算分析★

呂 娜 殷玉沉 孫玉周

(中原工學(xué)院建筑工程學(xué)院，河南 鄭州 450007)

為了探究應(yīng)變梯度的分布規(guī)律，建立新舊坐標(biāo)系下平面矢量的坐標(biāo)轉(zhuǎn)換公式，應(yīng)用鏈?zhǔn)椒▌t，推導(dǎo)了新坐標(biāo)系下應(yīng)變梯度的變換關(guān)系式，分析并求解出了應(yīng)變梯度的極值情況，為應(yīng)變梯度傳感器的使用提供理論依據(jù)。

應(yīng)變梯度，鏈?zhǔn)椒▌t，坐標(biāo)轉(zhuǎn)換，極值

1 概述

人類的現(xiàn)代化步伐離不開工程的現(xiàn)代化發(fā)展，無論是航空航天、地球海洋、冶金化工，還是地質(zhì)巖礦、建筑結(jié)構(gòu)、電力石油，每一類工程的實(shí)現(xiàn)都以工程力學(xué)為基礎(chǔ)，從最初的設(shè)計(jì)到成品的安全監(jiān)測，都離不開工程結(jié)構(gòu)的力學(xué)分析。在土木工程領(lǐng)域中，應(yīng)用最為廣泛的材料是混凝土，混凝土作為一種混合材料，其內(nèi)部骨料、水泥石上都含有一定的微裂紋或氣泡，隨著混凝土變形的發(fā)展，其內(nèi)部微裂紋和氣泡也相應(yīng)發(fā)展、擴(kuò)散直至貫通，形成宏觀裂縫[1]。裂縫作為土木工程結(jié)構(gòu)中最為常見的一種現(xiàn)象，不管是鋼筋混凝土結(jié)構(gòu)還是瀝青混凝土結(jié)構(gòu)或鋼結(jié)構(gòu)，在使用過程中都會有不同程度的裂縫出現(xiàn)。不同結(jié)構(gòu)部位、不同寬度的裂縫對結(jié)構(gòu)的承載能力、耐久性會產(chǎn)生不同程度的影響。

水泥混凝土的裂縫主要包括溫度裂縫、材料自收縮裂縫以及外部荷載或結(jié)構(gòu)變形作用下結(jié)構(gòu)內(nèi)力引起的裂縫。不管是何種裂縫，歸根結(jié)底其產(chǎn)生的原因在于該處混凝土的拉應(yīng)變超過了材料的極限拉應(yīng)變，材料發(fā)生局部受拉破壞。結(jié)構(gòu)在施工、使用過程中是否出現(xiàn)裂縫、在什么位置出現(xiàn)以及裂縫寬度的大小，是結(jié)構(gòu)監(jiān)測中迫切需要解決的問題。在結(jié)構(gòu)損傷監(jiān)測中，大多通過對應(yīng)變進(jìn)行測量和分析以確定混凝土中裂縫的產(chǎn)生和生長。現(xiàn)有的各類應(yīng)變傳感器測量應(yīng)變時，均假設(shè)所測量區(qū)域內(nèi)的應(yīng)變?yōu)榫鶆蚍植迹@顯然有悖于損傷區(qū)域應(yīng)變分布的真實(shí)情況。對混凝土類材料局部化破壞的研究表明，材料在發(fā)生破壞時，往往不會產(chǎn)生很明顯的塑性屈服，而是由于內(nèi)部微裂隙、微空洞等缺陷的擴(kuò)展和連通使材料剛度降低，非線性變形積累，最終造成材料局部化損傷和破壞，在剪切帶內(nèi)部，常常發(fā)現(xiàn)有較大的應(yīng)變梯度存在[2-6]。研究顯示應(yīng)變梯度相對于應(yīng)變其變化更加劇烈，應(yīng)變梯度顯然更容易快速、直觀地反映出損傷的位置，應(yīng)變梯度信息對于結(jié)構(gòu)健康監(jiān)測具有不言而喻的重要價值[7]。通過對多峰反射光譜進(jìn)行分析，有可能獲得幾毫米范圍內(nèi)的結(jié)構(gòu)局部非均勻應(yīng)變或應(yīng)變梯度的變化情況，這一特性表明，光纖布拉格光柵的性能顯著優(yōu)于現(xiàn)有的用于結(jié)構(gòu)損傷識別的其他各類應(yīng)變傳感元件[8]。為了探究應(yīng)變梯度的分布規(guī)律，本文通過建立新舊坐標(biāo)系下平面矢量的坐標(biāo)轉(zhuǎn)換公式，應(yīng)用求導(dǎo)的鏈?zhǔn)椒▌t，推導(dǎo)新坐標(biāo)系下應(yīng)變梯度的變換關(guān)系式。基于坐標(biāo)轉(zhuǎn)換推導(dǎo)出的任意方向上應(yīng)變梯度表達(dá)式，分析討論該狀態(tài)下應(yīng)變梯度的極大值、極小值及其對應(yīng)方向，為應(yīng)變梯度傳感器的使用提供理論依據(jù)。

2 應(yīng)變梯度的計(jì)算

在Oxy坐標(biāo)系中，方向矢量r(x,y)經(jīng)過變形為r′(x′,y′)，其平面應(yīng)變分量為[9]：

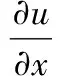
(1)

假設(shè)將坐標(biāo)軸旋轉(zhuǎn)α角(逆時針方向?yàn)檎?，得到新坐標(biāo)系Ox′y′，如圖1所示。M點(diǎn)的位移矢量U在新坐標(biāo)軸x′和y′上的投影為u′和v′，位移矢量U應(yīng)與坐標(biāo)系的選擇無關(guān)，矢徑也與坐標(biāo)系的選擇無關(guān)[10]，因此可得:

u′=ucosα+vsinα
v′=-usinα+vcosα
x=x′cosα-y′sinα
y=x′sinα+y′cosα

(2)

x=(x,y)表示原始參考構(gòu)形，x′=(x′,y′)表示當(dāng)前構(gòu)形。從變形前到變形后的變形映射由x′=x′(x)定義，一階變形梯度F和二階變形梯度G分別為:

(3)

(4)

將式(1)代入式(3)可得:

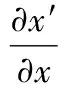
(5)

將式(1)代入式(4)，G111可表示為:

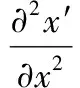
(6)

同理可得:

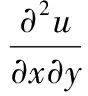
(7)

上式即為應(yīng)變梯度表達(dá)式，則在新坐標(biāo)系Ox′y′下應(yīng)變梯度表示為:

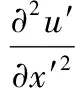
(8)

若把u′和v′看作是x和y的函數(shù)，x和y又是x′和y′的函數(shù)，由求導(dǎo)鏈?zhǔn)椒▌t[11]，G111′可表示為:

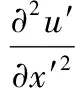
(9)

上式中的偏導(dǎo)數(shù)由式(2)求出為:

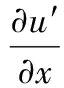
(10)

將式(6),式(7)和式(10)代入式(9)，整理后可得:

G111′=G111cos3α+G222sin3α+(G211+2G112)sinαcos2α+(2G212+G122)sin2αcosα

(11)

同理可得:

G112′=G112cos3α-G212sin3α+(-G111+G212+G122)sinαcos2α+(-G211-G112+G222)sin2αcosα

G122′=G122cos3α+G211sin3α+(-2G112+G222)sinαcos2α+(G111-2G212)sin2αcosα

G211′=G211cos3α-G122sin3α+(-G111+2G212)sinαcos2α+(-2G112+G222)sin2αcosα

G212′=G212cos3α+G112sin3α+(-G211-G112+G222)sinαcos2α+(G111-G212-G122)sin2αcosα

G222′=G222cos3α-G111sin3α+(-2G212-G122)sinαcos2α+(G211+2G112)sin2αcosα

(12)

上式即為坐標(biāo)轉(zhuǎn)換時應(yīng)變梯度的轉(zhuǎn)換規(guī)律，將G111′記為Gα，式(11)又可寫成:

Gα=G111cos3α+G222sin3α+(G211+2G112)sinαcos2α+(2G212+G122)sin2αcosα

(13)

3 應(yīng)變梯度的分析

式(13)表明，平面應(yīng)變梯度Gα隨α角的改變而變化，即Gα是α的函數(shù)，利用式(13)便可確定應(yīng)變梯度的極值和它所在的角度。

式(13)對α求導(dǎo)可得:

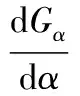
(14)

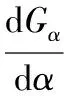
-3G111sinα0cos2α0+3G222sin2α0cosα0+(G211+2G112)(cos3α0-2sin2α0cosα0)+(2G212+G122)(2sinα0cos2α0-sin3α0)=0

(15)

方程式(15)的解α0即為應(yīng)變梯度的極值位置，為了確定極值類型，將式(14)對α取導(dǎo)數(shù)，得:

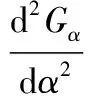
(16)

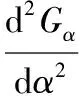
解方程式(15)如下，令α0≠Nπ，N為整數(shù)，方程兩端同時除以cos3α0，可得:

-(2G212+G122)tan3α0-(2G211+4G112+3G222)tan2α0+2(2G212+G122-3G111)tanα0+(G211+2G112)=0

(17)

分別令a=-(2G212+G122)，b=-(2G211+4G112+3G222)，c=2(2G212+G122-3G111)，d=G211+2G112，a≠0代入方程可得:

atan3α0+btan2α0+ctanα0+d=0

(18)

由卡爾丹公式解方程式(18)可得:

(19)

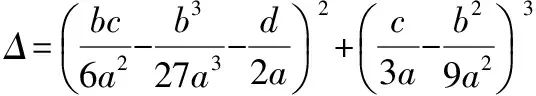
1)當(dāng)Δ>0時，方程有一個實(shí)根和兩個共軛復(fù)根，由于方程有工程實(shí)際背景，只取實(shí)根即tanα1。

2)當(dāng)Δ=0時，方程有三個實(shí)根，此時有兩種情況：

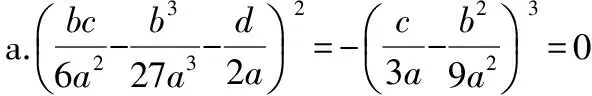
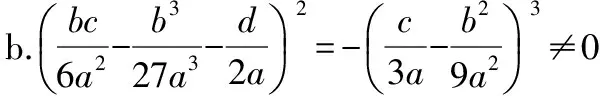
3)當(dāng)Δ<0時，方程有三個不等的實(shí)根，即tanα1,tanα2,tanα3。

4 結(jié)語

通過對應(yīng)變梯度狀態(tài)的計(jì)算和分析，本文得出結(jié)論如下：

1)建立了新舊坐標(biāo)系下平面矢量的坐標(biāo)轉(zhuǎn)換公式，應(yīng)用求導(dǎo)的鏈?zhǔn)椒▌t，推導(dǎo)了新坐標(biāo)系下應(yīng)變梯度的變換關(guān)系式；

2)分析了某變形狀態(tài)的應(yīng)變梯度G，得出了該狀態(tài)下任意方向的應(yīng)變梯度表達(dá)式；

3)分析了某變形狀態(tài)的應(yīng)變梯度G，討論了該狀態(tài)下應(yīng)變梯度的極大值、極小值及其對應(yīng)方向。

以上結(jié)論為光纖光柵應(yīng)變梯度傳感器的使用提供了理論依據(jù)。

[1] 陸 飛.分布式光纖傳感技術(shù)在土木工程結(jié)構(gòu)監(jiān)測中的應(yīng)用研究[D].南京：東南大學(xué),2007.

[2] 趙吉東,周維垣,劉元高.巖石類材料應(yīng)變梯度損傷模型研究及應(yīng)用[J].水利學(xué)報,2002,33(7):70-74.

[3] 剡公瑞.巖石、混凝土類材料的斷裂機(jī)理、模型研究及其工程應(yīng)用[D].北京：清華大學(xué),1994.

[4] 尚嘉蘭,李廷芥.巖石細(xì)觀損傷破壞的觀測研究[J].實(shí)驗(yàn)力學(xué),1999,14(3):373-383.

[5] Hill R,Hutchinson J W.Bifurcation phenomena in the plane tension test[J].Journal of the Mechanics & Physics of Solids,1975,23(45):239-264.

[6] Rudnicki J W,Rice J R.Conditions for the localization of deformation in pressure-sensitive dilatant materials[J].Journal of the Mechanics & Physics of Solids,1975,23(6):371-394.

[7] 鮑金秋,駱 英.一種基于應(yīng)變梯度監(jiān)測Ⅰ型裂紋的方法[J].力學(xué)與實(shí)踐,2015,37(6):704-707.

[8] 鄭世杰.結(jié)構(gòu)健康監(jiān)測:理論建模和計(jì)算智能方法[M].北京：國防工業(yè)出版社,2014.

[9] 徐秉業(yè),劉信聲.應(yīng)用彈塑性力學(xué)[M].北京：清華大學(xué)出版社,1995.

[10] 劉鴻文.材料力學(xué)[M].第5版.北京：高等教育出版社,2011.

[11] 徐 信.用鏈?zhǔn)椒▌t求復(fù)合函數(shù)的導(dǎo)數(shù)[J].中國遠(yuǎn)程教育,1983(1):6-9.

Calculationandanalysisofplanestraingradientbasedonchainrule★

LvNaYinYuchenSunYuzhou

(SchoolofCivilEngineeringandArchitecture,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)

In order to explore the distribution law of strain gradient, the coordinate transformation formula of plane vector in new and old coordinate system is established. By using chain rule, the transformation relation of strain gradient in new coordinate system is deduced, and the extreme value of the strain gradient is analyzed and solved, which provides the theoretical basis for the application of strain gradient sensor.

strain gradient, chain rule, coordinate transformation, extreme value

1009-6825(2017)32-0021-03

2017-09-01 ★:國家自然科學(xué)基金(11472316)；河南省科技創(chuàng)新人才項(xiàng)目(164200510020)

呂 娜(1991- )，女，在讀碩士； 殷玉沉(1990- )，男，在讀碩士； 孫玉周(1974- )，男，博士，教授

TU311.4

A