風電場噪聲的預測模型

桂 青

（上海勘測設計研究院有限公司，上海 200434）

風電場噪聲的預測模型

桂 青

（上海勘測設計研究院有限公司，上海 200434）

本文采用浙江大學對NASA修正模型進行預測，綜合考慮葉片后緣形狀影響、Ka系數的頻譜修正、指向性系數等因素，建立了聲源輻射指向性預測模型。根據對某一風電場現場監測結果可知，當噪聲預測點距離風電機組較遠（水平距離大于2倍風輪半徑）時，預測值與監測值擬合系數達到0.95以上，預測效果較好，因此NASA修正模型能較好地預測風電場遠場區的噪聲水平。

風電場；噪聲預測；NASA修正模型；指向性系數

21世紀以來，能源危機成為全球化的重點、難點問題，尋求可再生資源成為各國能源開發關注的焦點。風能資源具有可再生、可循環、可持續、無污染的特點，具有較好的經濟開發價值，是未來可再生資源的重點發展方向之一，日益受到各國資源開發管理部門的重視[1]。風力發電是我國能源發展戰略和調整電力結構的重要措施之一，國家發展與改革委員會提出了到2020年全國建設2.1億kW風電裝機的目標[2-3]。然而，風電機組運轉過程中會形成氣動噪聲，產生風電場噪聲污染，進而對周邊居民生活、工作等方面造成不同程度的影響[4]。

目前，我國在環評噪聲預測中多采用單一的、非指向性的點聲源預測模式，預測模型及結果常常受到質疑。本文采用浙江大學對NASA修正模型進行預測，綜合考慮葉片后緣形狀影響、Ka系數的頻譜修正、指向性系數等因素，建立了聲源輻射指向性預測模型[5]，并以某一風電場現場監測數據為例驗證其合理性。

1 模型研究

1.1 模型簡介

風電噪聲污染主要來自于風電機組葉片轉動，而風電機組機械噪聲值相對較小，因此風電機組噪聲預測時通常僅考慮葉片氣動噪聲。美國航空航天局（National Aeronautics and Space Administration，NASA）通過FW-H方程頻域求解方式研究開發了一種風電機組噪聲預測模型，我國浙江大學以該模型為研究開發基礎和技術預測平臺，針對我國自主生產的風電機組工作運轉特性，對NASA風電噪聲模型進行修正和調試，研發出適合我國風電機組噪聲輻射特性的噪聲預測模型。

1.2 基本形式

在NASA模型中，風電機組的氣動噪聲包括吸入湍流噪聲、湍流邊界層噪聲以及脫落渦噪聲。

1.2.1 吸入湍流噪聲

吸入湍流噪聲的計算公式為：

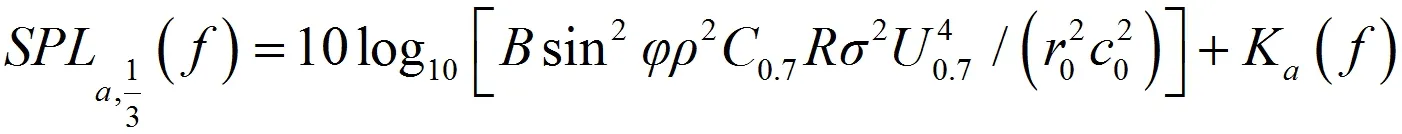
SPLa,1/3(f)表示吸入湍流噪聲1/3倍頻程頻帶聲壓級，f為1/3倍頻程中心頻率，B為葉片數量，φ為輪縠中心與預測點連線和風葉轉動平面間的夾角。ρ為空氣密度，C0.7為0.7倍風輪半徑處的葉片弦長，R為風輪半徑，σ2為平均湍流強度，U0.7為0.7倍風輪半徑處的自由層速率，r0為輪縠中心到預測點的直線距離，c0為聲速，S為斯特勞哈爾數，S=16.6，h為輪轂高度，Ka(f)為與頻率相關的比例因子。

fpeak=SU0.7/(h-0.7R)當f=fpeak時，Ka(f)達到最大值。

1.2.2 湍流邊界層噪聲

湍流邊界層噪聲的計算公式為：

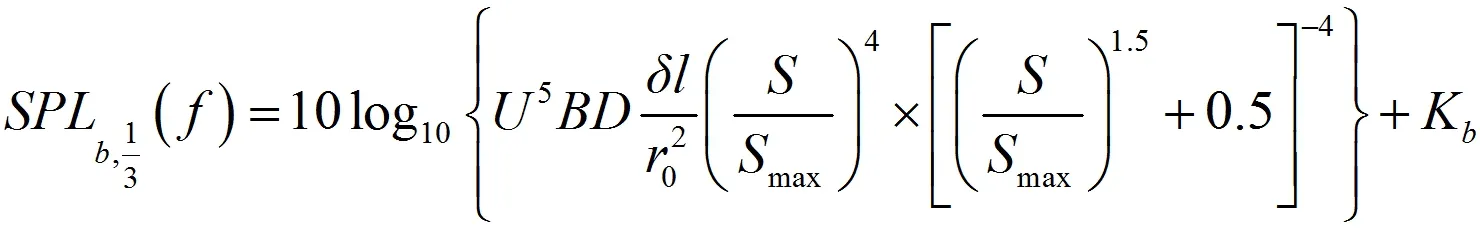
SPLb,1/3(f)表示吸入湍流噪聲1/3倍頻程頻帶聲壓級，U為自由層速率，δ為邊界層厚度，l為葉片單元的翼展，S為斯特勞哈爾數，S=fδ/U，Smax=0.1，Kb為比例因子，Kb=5.5。

指向性因數的計算公式為：

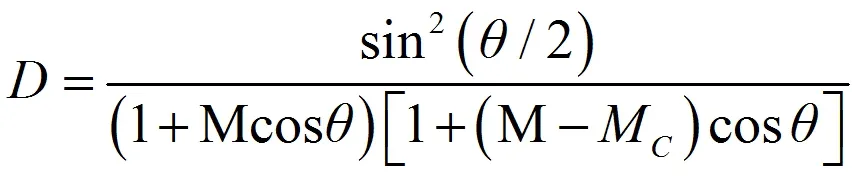
D為指向性因數，θ為聲源與預測點連線與其風葉轉動平面間的夾角，M為翼展馬赫數，Mc為對流馬赫數，Mc=0.8M。

1.2.3 脫落渦噪聲

脫落渦噪聲的計算公式為：

SPLc,1/3(f)表示吸入湍流噪聲1/3倍頻程頻帶聲壓級，t為葉片邊緣厚度，ψ為聲源與預測點連線與風葉轉動平面水平投影間的夾角，Kc(f)為與頻率相關的比例因子。

1.2.4 聲級疊加

聲級疊加的計算公式為：

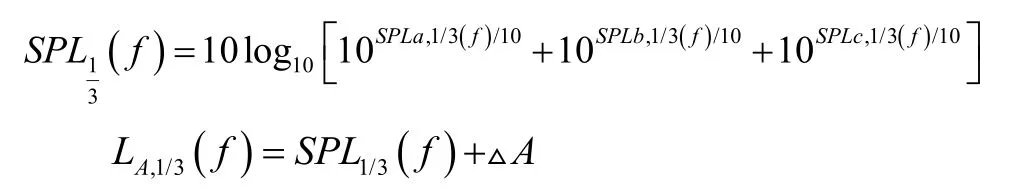
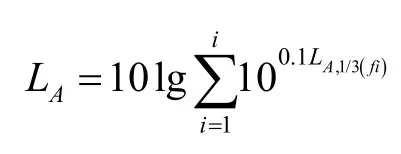
1.3 模型修正

NASA模型數據來源于MOD-2風電機組，而MOD-2風電機組含有兩片鈍形后緣的葉片，但隨著可再生資源生產技術的日益進步，風力發電技術的成熟，風電機組葉片在其設計、生產、制造等方面上有了較大創新，我國風電場目前使用三片尖形后緣葉片的風電機組。較兩片鈍形后緣的葉片，三片尖形后緣葉片在漿尖處有所改進，葉片輻射噪聲有所降低。因此需要對NASA模型進行修正，以符合我國風電機組噪聲預測。

（1）葉片后緣形狀影響修正

根據圖1可知，風電機組產生的脫落渦噪聲的頻率范圍相對于吸入湍流噪聲和湍流邊界層噪聲較窄，僅在高頻段產生一個峰值。這個峰值主要由風電機組鈍形后緣的葉片產生，而我國風電場使用的三片尖形后緣葉片產生的脫落渦噪聲并不明顯，在噪聲預測中可將脫落渦噪聲忽略。

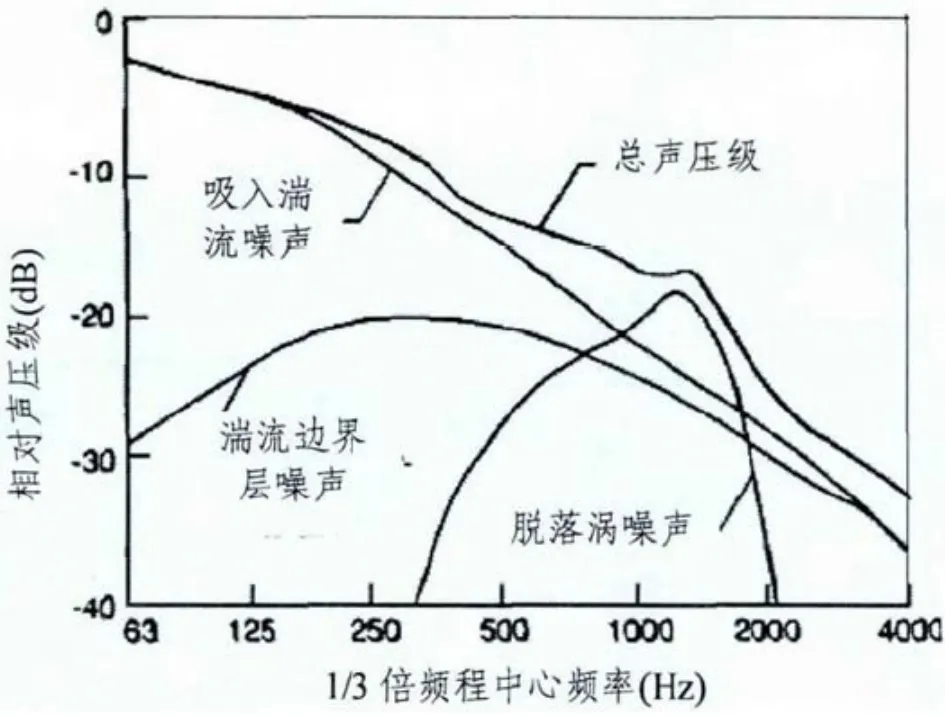
圖1 NASA模型中三部分噪聲貢獻值示意圖

（2）Ka系數的頻譜修正

NASA模型采用中的MOD-2風電機組額定功率2.5 MW，輪轂高度61 m，轉輪直徑91.4 m，測量時葉片轉速0.59 HZ，形成了吸入湍流噪聲中的Ka(f)曲線。而我國自主研發的風電機組額定功率在1 MW～2.5 MW之間，由3片葉片組裝而成，與MOD-2風電機組在葉片數量、翼型形狀、葉片表面粗糙度、葉片材質存在差異，致使產生的葉片輻射噪聲和頻譜有所差異。

根據如東風電機組（額定功率1.5 MW）的現場噪聲監測數據，對吸入湍流噪聲公式中的Ka(f)曲線進行修正，如圖2所示。

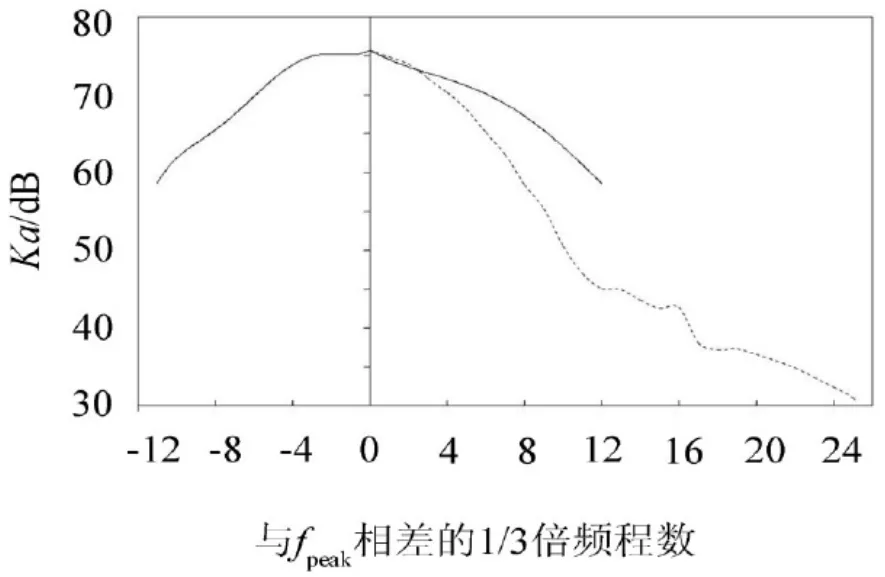
圖2 修正前后的Ka(f)曲線

（3）指向性系數

在NASA預測模型中，噪聲預測結果僅與測點位置到聲源的距離有關，與所處風向無關。而實際現場監測中，上風向測點與下風向測點監測結果有所差異，通常情況下，上風向測點監測值較下風向監測值低。因此，需對模型中指向性系數進行修正。

LA,P為修正前P點A聲級，L'A,P為修正后P點A聲級，LA,Q為ɑ=0°方向距塔基水平距離d處Q點修正前A聲級。

1.4 預測工況及源強

1.4.1 預測工況

根據崇明縣侯家鎮氣象臺有關資料統計，區域年主導風向為東南風，多年平均風速2.8～3.2 m/s。建設單位提供的某風電場年運行負荷情況如表1所示。由表可知，風機不運行工況概率為14.45%，風機年運行負荷小于20%工況概率為38.01%，風機負荷介于20%和40%工況之間概率為20.56%，風機負荷介于40%和60%工況之間概率為9.80%，風機負荷介于60%和80%工況之間概率為6.52%，風機負荷大于80%工況概率為10.66%，最不利工況出現概率較小。

1.4.2 源強分析

設備廠商提供了風機超過額定風速運行（滿負荷）工況下的風機噪聲源強。最不利工況下（風速12 m/s及以上），如表2所示，風機輪轂及葉輪處噪聲值為102 dB(A)，通風設備處噪聲值為86 dB(A)。

1.4.3 聲源指向性指數

考慮到順風有利于聲傳播，上風向噪聲小于下風向噪聲的實際情況，聲源指向性指數計算時，取ɑ=0°進行計算，計算得到聲源指向性指數為0.31。

1.4.4 計算參數

風力發電輪轂高度90 m，葉片直徑121.5 m，90 m高度處空氣密度為1.208 kg/m3，80 m及以上處15 m/s風速區間湍流強度（參考70 m高度值）不超過0.10。

2 模型預測值與實測值比較

滿負荷運行工況下，不同距離條件下風機噪聲實測和預測結果如表3所示，其中預測結果是在預測值的基礎上疊加了背景值。將滿負荷運行工況下噪聲實測結果與噪聲預測結果進行對比分析[6]。從圖3、圖4可以看出，不論是晝間還是夜間，風機噪聲實際測量值與預測值差異均隨距離增大逐漸減小，在距離風電機組150 m以上時，實際測量得出的風機噪聲隨距離衰減變化趨勢同預測結果幾乎一致。而距風機1 m、100 m處風機晝間實際測量值與預測值相差較大，其可能與近場區噪聲受多種因素影響有關，修正模型預測效果有限。當噪聲預測點距離風電機組較遠（水平距離大于2倍風輪半徑）時，預測值與監測值擬合系數達到0.95以上，預測效果較好，因此NASA修正模型能較好地預測風電場遠場區噪聲水平。

表1 風機年運行負荷情況(2015.7～2016.2)

表2 最不利工況下風機噪聲源強

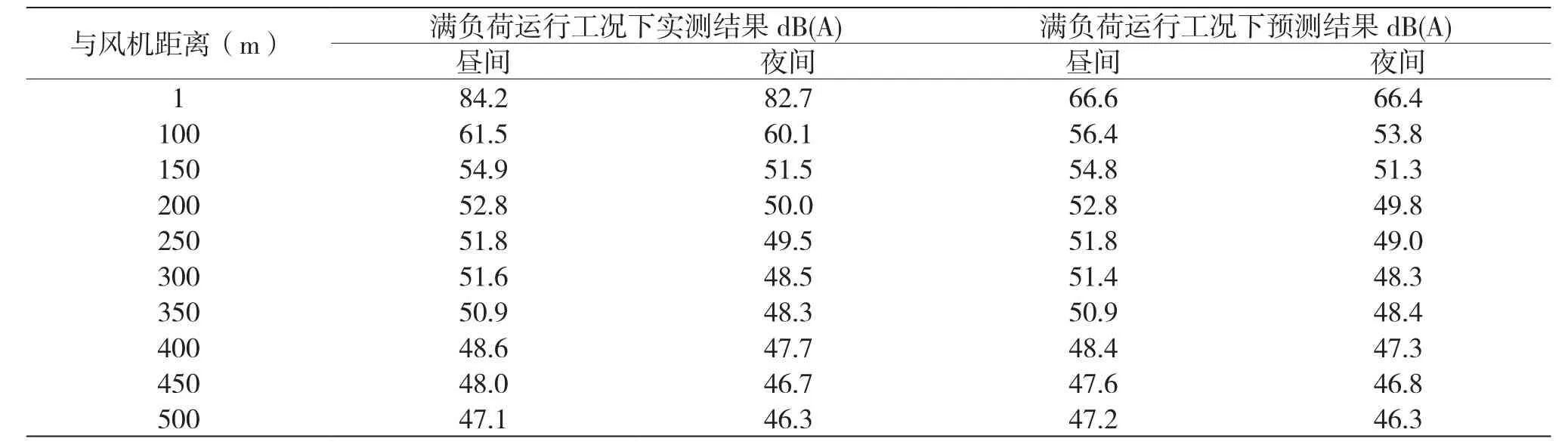
表3 不同距離條件下風機噪聲實測和預測結果

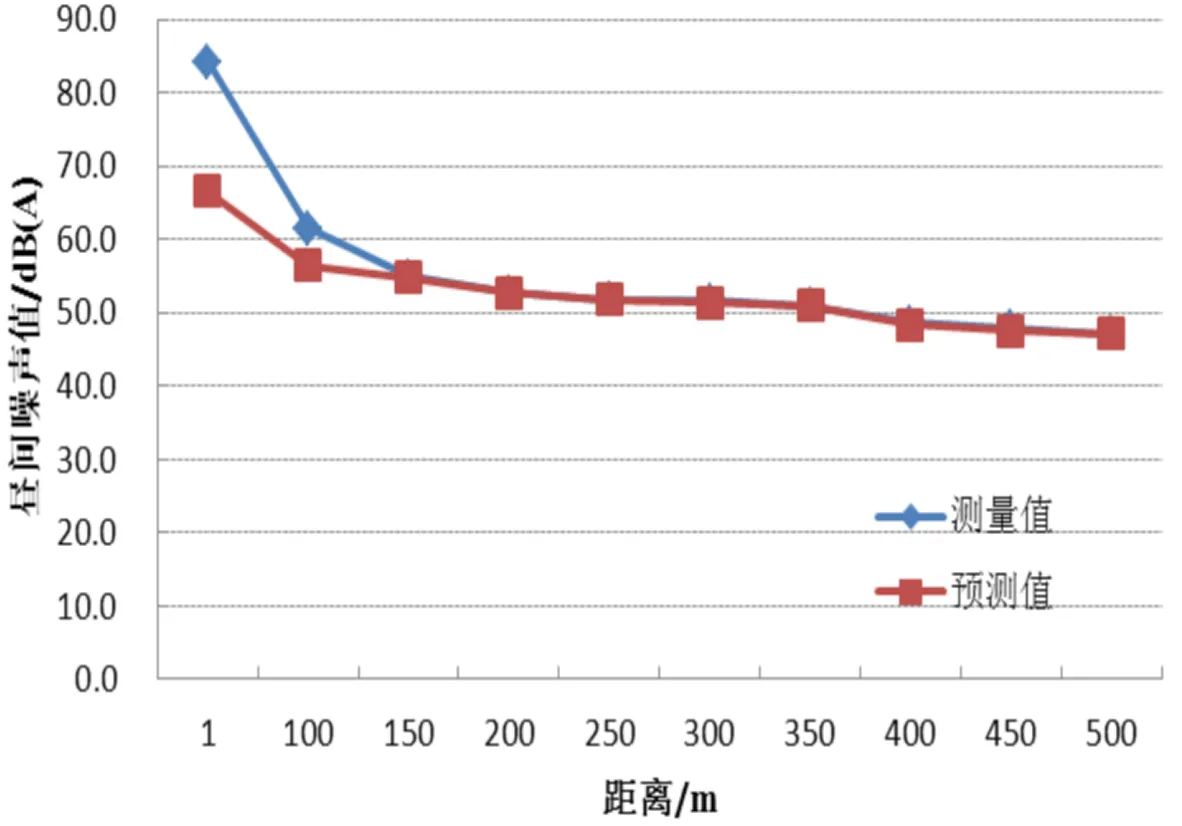
圖3 風機晝間噪聲隨距離衰減變化趨勢

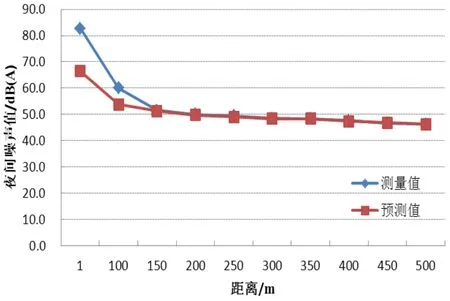
圖4 風機夜間噪聲隨距離衰減變化趨勢

3 結語

本文采用浙江大學對NASA修正模型進行預測，綜合考慮葉片后緣形狀影響、Ka系數的頻譜修正、指向性系數等因素，建立了聲源輻射指向性預測模型，并以某一風電場現場監測數據為例驗證其合理性。根據風電機組噪聲的實際監測結果，當噪聲預測點距離風電機組較遠（水平距離大于2倍風輪半徑）時，預測值與監測值擬合系數達到0.95以上，預測效果較好，因此NASA修正模型能較好地預測風電場遠場區噪聲水平。

1 徐 婧.風電機組噪聲預測[D].杭州：浙江大學，2012.

2 國家發展改革委委員會.可再生能源中長期發展規劃[Z]，2016.

3 中國可再生能源學會風能專業委員會.2010年中國風電裝機容量統計[R].北京：中國可再生能源學會風能專業委員會，2011.

4 魏 楨，鄧院昌，楊正浩.基于Elman神經網絡的風電場噪聲預測模型[J].水電能源科學，2015，5（33）：204-206．

5 仇 豐，廖琦琛，丁明明，等.風電場噪聲預測模型[J].噪聲與振動控制，2012，（2）：118-122．

6 上海勘測設計研究院有限公司.北堡二期風電場項目環境影響報告表[R].上海：上海勘測設計研究院有限公司，2016.

Predictive model of wind farm noise

Gui Qing
(Shanghai Investigation Design and Research Institute Co., Ltd., Shanghai 200434, China)

The modified NASA model by Zhejiang University was applied for prediction of wind turbine generator noise.Noise prediction model is established by considering the influence of wind turbines with trailing edges，modification of parameter Ka and directivity index.According to the measured noise data of domestic operating wind turbine sets，when the distance between rotor center and receiver is greater than 2 times the rotor blade radius, the difference between the measurement values and the predicted values of the modified model is small（Fitting coefficient＞0.95）.So the modified NASA model had a better prediction accuracy for far noise distribution in wind power field.

wind farm; noise prediction; NASA correction model; directivity coefficient

TM614

A

1008-9500(2017)06-0099-04

2017-04-10

桂青(1984-)，女，安徽蕪湖人，工程師，從事環境影響評價工作。