緩粘結預應力混凝土T梁預應力效應分析

李 可

(常德市穿紫河建設開發有限公司，湖南 常德 415000)

緩粘結預應力混凝土T梁預應力效應分析

李 可

(常德市穿紫河建設開發有限公司，湖南 常德 415000)

進行了2根預應力混凝土T梁的長期試驗，通過對2種不同預應力施工工藝的混凝土梁在預應力施加后21 d的觀測，研究了混凝土梁的跨中應變、預應力損失、撓度等方面的內容并進行了對比，在疊加法的基礎上提出了計算存梁期間預應力混凝土簡支梁撓度的理論方法．試驗結果表明，緩粘結預應力梁與普通預應力梁的實測應變、撓度值發展規律基本相同．通過計算值與理論值的分析比較，驗證了本試驗理論計算的可靠性和精度，表明緩粘結預應力梁在存梁期有著與普通預應力混凝土梁相同的預應力效應．

預應力混凝土梁；緩粘結；撓度；預應力效應

緩粘結預應力混凝土技術克服了傳統預應力混凝土技術的缺點，具有顯著的技術優勢和推廣價值．鋼筋與混凝土在前期相對獨立，其施工同無粘結預應力混凝土一般便捷[1-3]；隨著緩凝材料強度的增長，鋼筋與混凝土開始協同受力，其抗震性能同有粘結預應力混凝土一般良好[4-6]．因其優異的性能廣泛應用于各類大跨徑預應力混凝土梁橋．為了避免預應力混凝土橋梁因收縮徐變和有效預應力大小等時程因素引起橋梁變形過大而影響結構的施工和正常服役，所引起的變形需控制在容許值范圍內[7-8]．因此，準確預估預應力混凝土橋梁的預應力效應，對工程實踐具有很強的指導意義．針對這種現狀，對比普通預應力混凝土梁(有粘結預應力混凝土梁)，本文研究了存梁期間緩粘結預應力混凝土梁的預應力效應．在疊加法的基礎上提出了計算存梁期間預應力混凝土簡支梁撓度的理論方法．

1 試驗方案

1.1 試件模型

本試驗對30 m標準梁按1︰3的比例進行縮尺得到試驗梁，研究了緩粘結預應力施工工藝對結構預應力效應的影響．共制作2片T梁，梁總長1 020 cm，計算跨徑1 000 cm．1#梁為緩粘結預應力混凝土梁，2#梁為普通預應力混凝土梁．混凝土設計強度等級為C40．梁高58 cm，翼板寬53 cm，腹板厚10 cm．共設置3根預應力筋，試驗梁截面尺寸和預應力筋布置如圖1所示．

1.2 試驗梁制作

試驗梁鋼筋骨架嚴格按照施工圖紙進行綁扎．采用木模支架在室內地面進行安裝．制作緩粘結預應力混凝土梁時，將事先用緩粘結膠粘劑包裹的預應力筋和非預應力筋按設計位置布置，一同綁扎，再澆筑混凝土．普通預應力混凝土梁則是先澆筑混凝土，并在其中預留孔道，將預應力筋穿入預留的孔道內．待混凝土養護9 d，強度達到設計強度等級的70%后，采用穿心式液壓千斤頂張拉預應力筋．預應力張拉力的控制采用千斤頂油表讀數和力傳感器讀數雙重校核，采用分級張拉，然后錨固．現場試驗梁如圖2所示．

圖1 預應力筋布置形式/cm

圖2 試驗梁現場圖

1.3 材料力學性能

試驗梁混凝土采用相同混合比，水︰水泥︰砂︰石︰減水劑=232.5 kg︰460 kg︰585 kg︰1 175 kg︰3.6 kg．澆筑試驗梁的同時澆筑混凝土試塊，與試驗梁在相同環境下進行養護．非預應力筋和箍筋均采用HPB235級鋼筋，預應力筋采用直徑為15.2 mm的1860級鋼絞線．混凝土和鋼筋的力學性能根據現行規范中規定的試驗方法測得[9-10]．分別如表1、表2所示．

1.4 試驗測試內容及測點布置

撓度變化由安裝在梁的L/3、L/2、2L/3截面處百分表測得．截面跨中混凝土應變變化由預埋在跨中截面頂板和底板內的鋼弦式應變計(a1，a2)測得．在梁的錨固端布置2個傳感器測得預應力大小．具體布置如圖3、圖4所示．

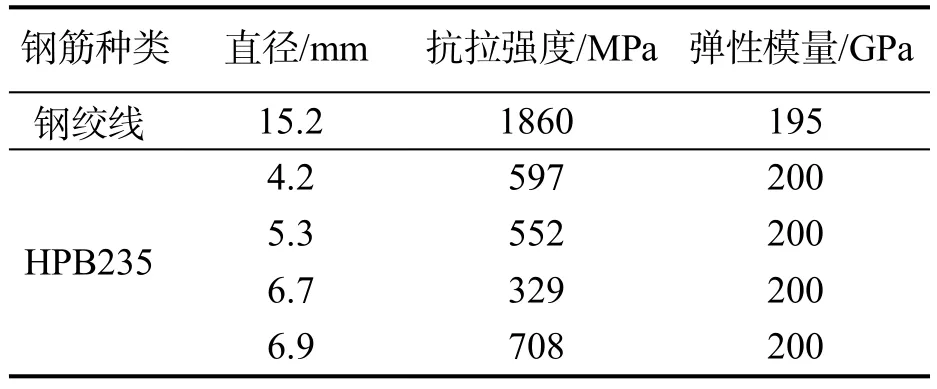
表1 鋼筋力學性能

表2 混凝土力學性能

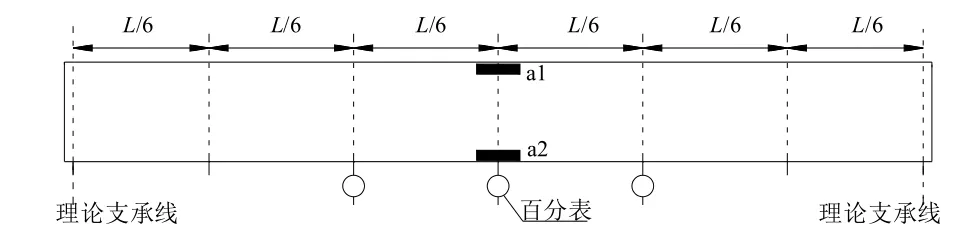
圖3 百分表及體內應變計布置

圖4 傳感器布置

2 試驗結果分析

2.1 體內應變

圖5是試驗梁存梁期間跨中體內應變變化的時程曲線．在試驗周期內，梁頂板和底板應變隨時間增長且全截面受壓．放置4 d時1#梁跨中頂板應變為2#梁的84 %，底板應變1#梁為2#梁的107.4 %；21 d時1#梁跨中頂板應變為2#梁的93 %，底板應變為2#梁的102.5 %．應變在預應力作用一段時間后以幾乎相同的速率增長，驗證了在線性徐變范圍內徐變與應力呈線性關系．

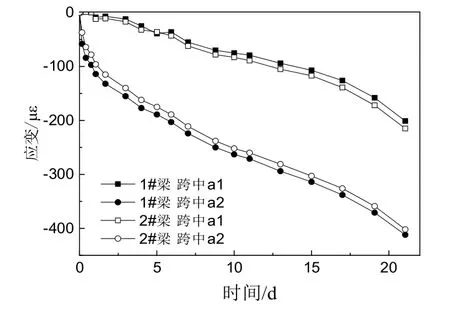
圖5 跨中體內應變時程曲線

2.2 預應力損失

圖6是試驗梁存梁期間預應力損失變化的時程曲線．預應力施加后，1#梁和 2#梁的預應力損失時程曲線發展趨勢基本一致，預應力損失在初期增長較快，后期損失仍有增長但速率有所減緩，總體發展趨勢相同，這是因為在預應力張拉初期由于錨具變形，混凝土局部受壓變形等原因導致在加載初期預應力損失較大；當2#梁放置4 d后傳4的預應力損失為2 kN，為傳2的95.2%．放置21 d后傳4的預應力損失為4.9 kN，為傳2的92.4%．普通預應力混凝土梁的預應力損失比緩粘結預應力混凝土梁的稍小．由于傳1產生了較大誤差，數據失效，不予以討論．

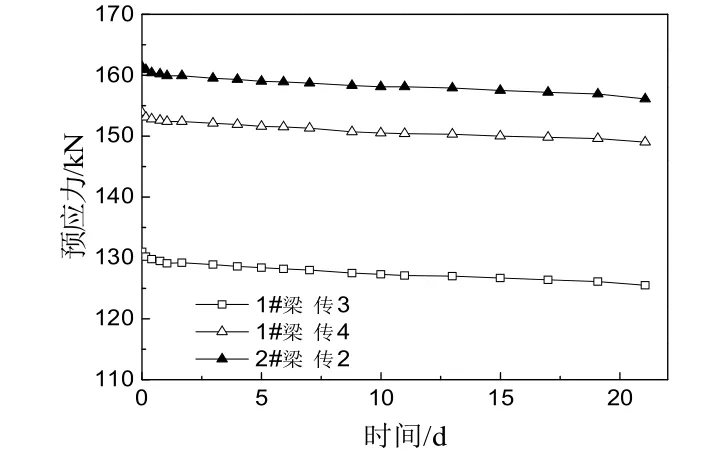
圖6 預應力損失時程曲線

2.3 預應力反拱撓度

圖7是試驗梁存梁期間跨中截面處反拱撓度變化的時程曲線．在試驗周期前2 d內反拱增長速率較大，2 d后增長速率減小，雖有稍許波動但總體趨于平穩，與混凝土的收縮徐變規律一致．緩凝砂漿粘結力的增強增大了預應力筋與管道壁的摩擦力，制約了反拱撓度的發展．放置21 d后，1#梁跨中截面反拱撓度變形實測值為 18.07 mm，為2#梁的85.2%．1 #梁、2 #梁的長期撓度分為其瞬時撓度的1.48、1.75倍，由混凝土收縮徐變引起的附加撓度不容忽視．

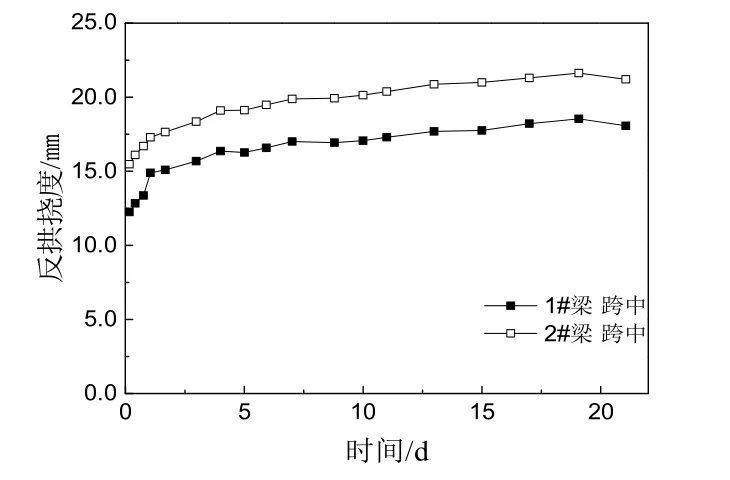
圖7 跨中反拱撓度時程曲線

2.4 徐變系數

圖8是試驗梁存梁期間跨中反拱徐變系數變化時程曲線，由實測數據可見，緩粘結應力混凝土梁反拱徐變系數比普通預應力混凝土梁大．在本試驗周期初期，緩凝砂漿與鋼筋無可靠粘結，預應力筋摩擦力較普通預應力筋小，所以1#梁徐變系數增長較2#梁快．后期緩凝砂漿與預應力筋完全粘結，1#梁、2#梁徐變系數增長速率幾乎相同，說明緩粘結預應力筋已具有和有粘結預應力筋相同的受力性能．持荷21 d后，1#梁的跨中體內徐變系數為0.981，較2#梁增大140%，1 #梁體內應變發展較2#梁快．

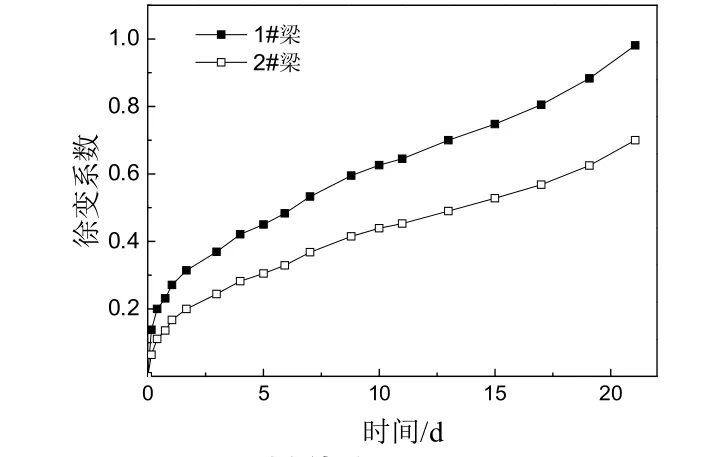
圖8 反拱徐變系數時程曲線

3 理論計算

3.1 徐變系數

混凝土結構在長期荷載作用下所產生的變形叫徐變，可用徐變系數、徐變度、徐變函數等來表示．當混凝土的加載齡期為t，在計算齡期為t時徐變產生的變形與瞬時彈性變形的比值為徐變系數．其表達式為

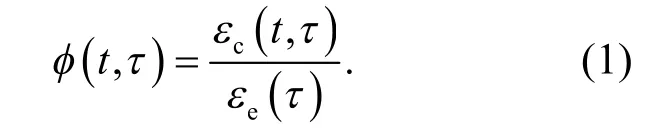
在加載齡期為t時對混凝土作用單位應力，在計算齡期t時刻產生的混凝土徐變應變為混凝土的徐變度，用C(t,t)表示．徐變度和徐變系數之間的關系為

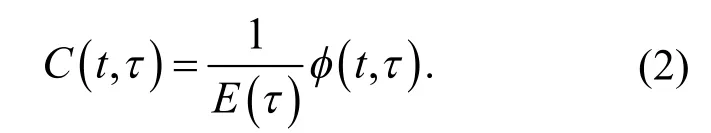
(1)在加載齡期為t時對混凝土作用單軸向單位常應力，在計算齡期t時刻產生的總應變為混凝土的徐變函數，用表示．表達式為

3.2 預應力混凝土梁的長期撓度變形

梁體預應力張拉后，產生的變形分成2部分：瞬間變形和長期變形．采用疊加法，預應力混凝土梁撓度的計算如下

(1)恒載引起的撓度fg1．混凝土梁結構的自重可簡化為均布荷載，根據結構力學原理，在該均布荷載作用下預應力混凝土梁的撓度fg1為

(2)預應力引起的撓度fy．鋼筋束有效預拉應力值ys為錨固控制應力減去所有的應力損失，利用圖乘法，有效預應力作用下梁的撓度為fy

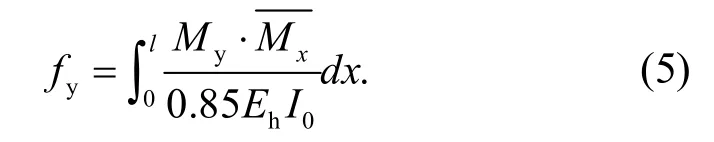
式中：My為有效預應力在任意截面x處所引起的彎矩值；為在任意截面處x由跨中作用單位力所引起的彎矩值；Eh為預應力張拉時混凝土的彈性模量．

(3)混凝土徐變引起的撓度．利用有效彈性模量法，在截面分析的曲率計算公式的基礎上，在t時間，梁跨中的撓度增量的表達式為

A、B分別代表梁左右兩端；M代表梁的跨中．(4)預應力混凝土梁長期變形的總撓度

3.3 撓度計算值與理論值的分析比較

對比實測數據，對本文所提出的理論計算方法作了誤差分析．結果為：普通預應力梁的平均誤差為4%，最大為8%(放置15 d時)．張拉預應力后，隨著緩凝砂漿粘結力的增強，緩粘結預應力筋與管道壁的摩擦力也隨之增大，制約了反拱撓度的發展．當緩凝砂漿完全粘結時，1#梁和 2#梁有著相同的受力環境，撓度發展速率相同．普通預應力梁的上拱撓度是緩粘結預應力梁撓度發展的上限，只需對普通預應力梁的撓度進行折減即可得到緩粘結預應力梁的撓度，但由于數據較少，對于緩粘結預應力梁反拱一般規律，需要更多的試驗數據做進一步的研究．本文中折減系數取0.82．本文試驗梁屬于全預應力梁，可忽略結構內部配筋對混凝土徐變的影響．總體來說，普通預應力梁上拱撓度理論值與實測值的吻合情況良好，驗證了本試驗理論計算的可靠性和精度，預測效果較好，有一定工程應用和科學研究價值．

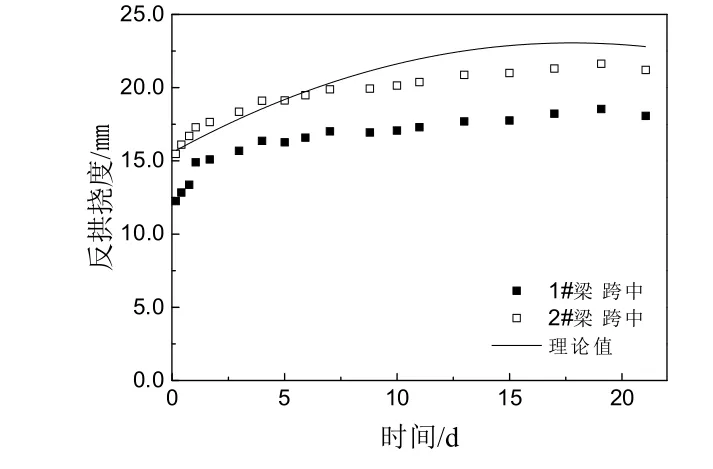
圖9 反拱撓度理論值與實測值時程曲線對比

4 結論

(1)在試驗周期內，緩粘結預應力混凝土梁的預應力效應引起的跨中應變、撓度、預應力損失和普通預應力混凝土梁發展規律基本相同，符合混凝土的收縮徐變規律．緩粘結預應力混凝土梁預應力效應引起的上拱度比普通預應力混凝土梁要小．

(2)1#、2#梁的長期撓度為其瞬時撓度的1.48、1.75倍，混凝土的收縮徐變引起的撓度占總撓度的比重較大，應盡量減少混凝土的收縮徐變．

(3)本試驗驗證了所用計算理論的可靠性和精度，因此推薦該理論作為預應力筋張拉后存梁期間考慮混凝土收縮徐變的預應力混凝土簡支梁撓度變形的計算公式，可為有關設計施工部門提供參考，為實際生產服務．

[1]陶學康. 無粘結預應力混凝土設計與施工[M]. 北京: 地質出版社, 1994．

[2]吳轉琴, 尚仁杰, 洪光. 緩粘結預應力鋼絞線與混凝土粘結性能試驗研究[J]. 建筑結構, 2013, 43(2): 68-70.

[3]王占飛, 胡正偉, 張子靜. 緩粘結預應力鋼筋摩擦系數試驗[J].沈陽工業大學學報, 2016, 38(3): 351-353.

[4]熊學玉, 黃煒一. 預應力混凝土收縮與徐變效應測試與分析[J]. 工業建筑, 2012, 42(4): 65-68.

[5]趙霄, 金凌志. 緩粘結預應力混凝土連續梁預應力損失計算及摩阻力研究[J]. 井岡山大學學報, 2011, 32(6):99-103.

[6]李金根, 熊小林, 李一心. 緩粘結預應力筋摩阻損失的試驗研究[J]. 建筑技術, 2008, 39(12): 943-946.

[7]吳桐. 預制預應力混凝土梁反拱度研究[D]. 哈爾濱: 東北林業大學, 2011.

[8]龔先兵, 向秋燕, 寧向向. 預應力鋼筋混凝T梁上拱度計算[J].鐵道科學與工程學報, 2011, 8(1): 107-112.

[9]GB/T 50081-2002, 普通混凝土力學性能實驗方法標準[S].

[10]GB/T 228-2002, 金屬材料室溫拉伸試驗方法[S].

(責任編校：徐贊)

Prestressing Effect Analysis of Retard-bonded Prestressed Concrete T-beams

LI Ke
(Chuanzi River Building amp; Development Co. Ltd. of Changde City, Changde, Hunan 415000, China)

To investigate the development laws of strain, prestress loss, and deflection of prestressed concrete beams under sustained load, long-term tests lasted 21 days on two prestressed concrete T-beams constructed by different construction technology were carried out. The calculation method of additional deflection in storage stage was proposed. The result of long-term tests shows that, the beam constructed by conventional technology and the new techniques of retard-bonded prestressed have similar development laws of strain and deflection. Comparing the calculated value with the theoretical value, the reliability and accuracy of the calculation method proposed here is verified. It shows that retard-bonded prestressed beams have similar prestressing effect with conventional prestressed concrete beams in storage stage.

retard-bonded; prestressed concrete; deflection; prestressing effect

TU442

A

10.3969/j.issn.1672-7304.2017.02.0004

1672–7304(2017)02–0016–04

2017-03-07

李可(1973-)，男，湖南常德人，工程師，主要從橋梁建設與管理研究，E-mail: 363601198@qq.com.