索-梁組合結構的面內外模態分析

沈忠偉

(國家電網湖南省電力公司檢修公司，長沙 410014)

索-梁組合結構的面內外模態分析

沈忠偉

(國家電網湖南省電力公司檢修公司，長沙 410014)

利用哈密頓變分原理以及結構動靜態構型的影響，建立了索-梁組合結構的約化運動學控制方程．根據求解得到的面內面外特征值方程，并通過分段函數的引入，研究了結構的模態函數的幾種形式．隨后，根據索-梁組合結構中索的模態函數，分析了面內外運動“局部模態”和“模態局部化”現象的產生．研究表明，在面內運動，在不考慮內共振情況下，面內運動索的大幅振動是由于“模態局部化”現象的產生，而根據特征值方程，“局部模態”只能出現在索-梁組合結構索的面外運動．

哈密頓變分原理；索-梁組合結構；局部模態

拉索在工程中應用廣泛，是一種主要只能承受拉力不能承受壓力的構件，拉索具有強度較高、松弛較低、質量較輕等特點，使得其能而較好地應用于各種建筑工程結構中，對于向大跨度方向發展的橋梁結構如斜拉橋，拉索是結構必用的構件．眾所周知，拉索的自然特性突出，如具有小質量、大柔度及較低的阻尼特性，在風、雨、地震及車輛等荷載作用下，使得斜拉索產生的大幅振動，可能會使得橋梁發生破壞，對橋梁結構的安全性和行車安全產生嚴重威脅．因此，斜拉索的非線性動力學問題一直以來都受到科研工作者的重視，是力學領域的研究熱點[1]．

近年來，Fujino[2]等、Gattulli[3]和趙躍宇等[4]建立了索-梁模型(主梁一端固定一端與斜拉索連接)，分別應用多尺度法研究了拉索的面外模態與梁的2個方向的彎曲模態之間的滿足1:1和2:1內共振模式．以往的文獻局限在將索的模態函數僅僅簡化為單索情況下的模態函數形式，使得對拉索在橋面和橋塔的運動研究較為簡單，從而根據可能的“局部模態”去分析斜拉索可能會產生的大幅振動．“局部模態”是指在結構振動中，只有索的振動．但是結構不同使得單索的模態函數與索-梁結構的模態函數也會有較大的差異[3-4]．這極有可能在理論上使得研究失去合理性，因此很難對拉索大幅振動及橋梁的破壞機理進行合理解釋，很難滿足未來超大跨度橋梁建設的工程需要[5-6]．目前較少有文獻根據索-梁組合結構的特性去分析可能的面內面外運動索的大幅振動，即從索的模態函數去分析可能出現的“局部模態”及“模態局部化”現象，而“模態局部化”是指在結構振動中，索的振動起主導作用，從而進一步揭示大幅振動產生的機理[7-8]．

基于上述原因，嚴格根據特征值方程，確定索的模態函數可以更好地理解局部模態，模態局部化現象，進一步揭示索的大幅振動產生原因[9]．

1 索-梁運動方程

索-梁模型如圖1所示.

圖1 索-梁組合結構的動靜態構型

索和梁的軸向位移可以忽略．因此，索-梁組合結構運動方程可以由哈密頓變分原理得出[10]：

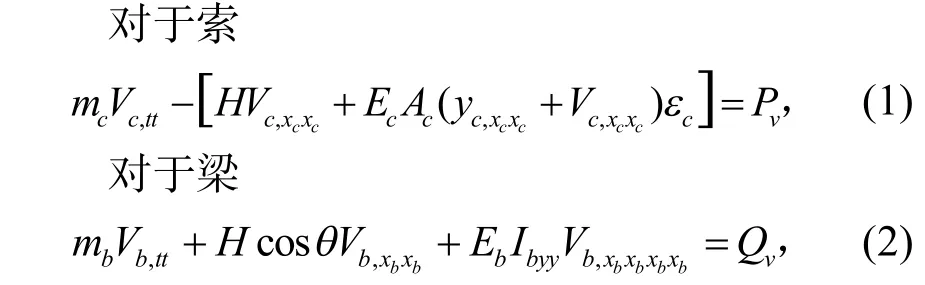
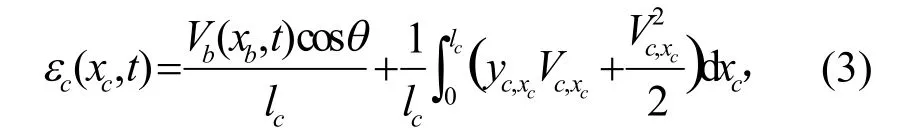
為了更好理解索-梁組合結構的動力學行為，對上述方程進行無量綱化，無量綱化參數如下：

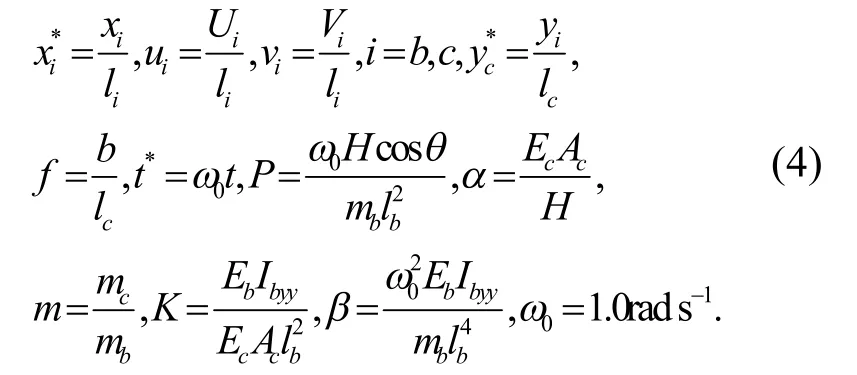
將式(4)代入索-梁運動方程以及邊界和連接條件，可以得到：

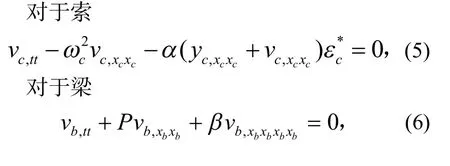
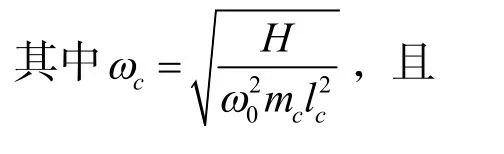
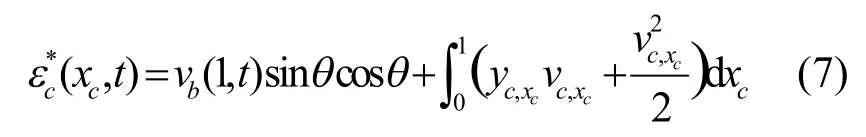
利用分離變量法可以得到整體系統的固有頻率以及索和梁的模態函數．對索和梁的位移函數進行分離變量

將式(8)代入索，梁運動方程以及邊界和連接條件中．

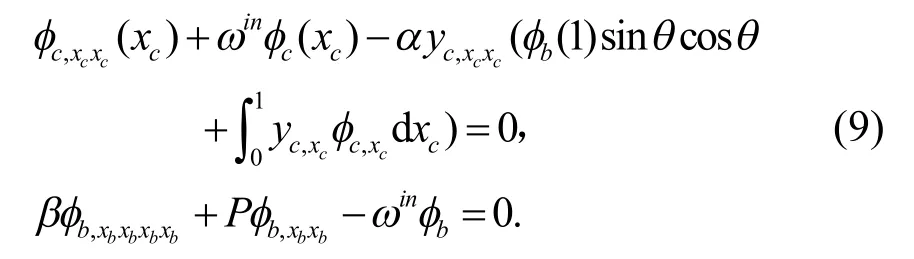
為了求解式(9)，引入索的輔助條件，假設

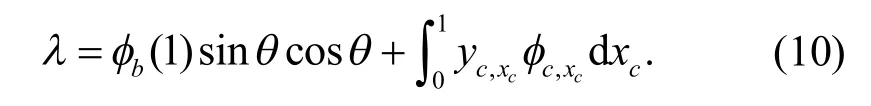
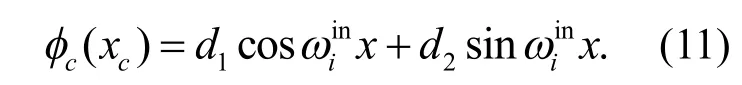
同樣地，考慮到l=0，在結構的連接點處力平衡條件可以表示成

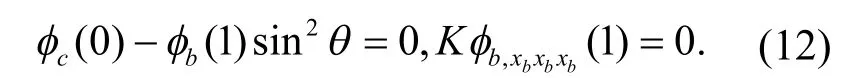
這意味著該情況下的剪力為零．類似地索的模態函數可以表示成

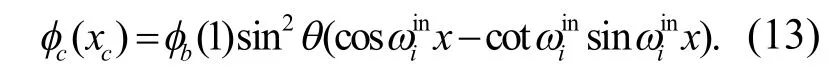
梁的邊界和連接條件為：

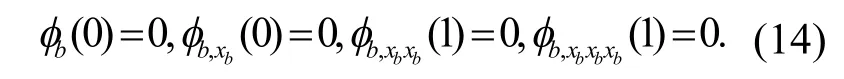
在l=0這種情況下，索-梁結構特征值方程可以通過式(14) 單獨的求得．同樣地，將式(13)代入式(10)，可以得到整體結構特征值方程：

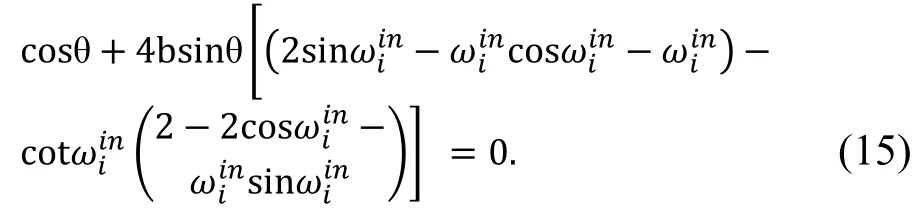
借助于軟件Mathematica，式(13)和式(15)可以分別得到求解，但是通過計算，2個方程得到的解答并不是相等的(見圖2)．因此，l=0這種情況是不存在的[3-6]．

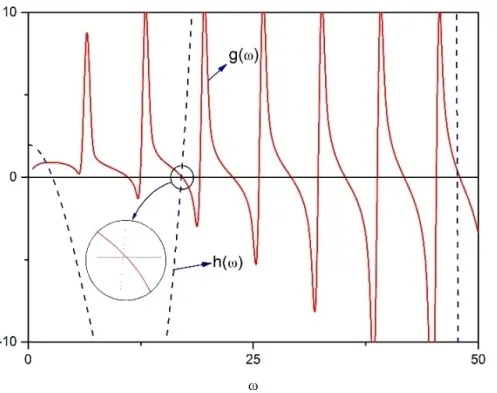
圖2 索-梁組合結構的特征值方程

2 局部模態與模態局部化

所以，根據特征值分析，我們可以得出結論，對于索梁組合結構面內振動，“局部模態”是不可能發生的，在不考慮內共振情形下，橋梁結構中索的大幅振動是由于發生了“模態局部化”現象．因此，對應著的索的模態函數應表示為

3 結論

本文根據變分原理，得到了索-梁組合結構的運動方程，根據分離變量法得到了結構的特征值方程，研究了索-梁組合結構面內面外振動特性．研究表明，“局部模態”只可能發生在面外運動，即所謂的大幅振動，為索的振動，因此梁的面外受力分力為零，即梁沒有任何位移，而完全表現為索的振動位移，即“局部模態”發生了，所以“局部模態”只可能發生在面外運動，“局部振動”不可能發生在面內．面內運動所謂的“局部模態”實際上應為 “模態局部化”現象，其對應著的模態函數應有所不同．

[1]Wgnitchai W, Fujino Y, Susumpow T. A non-linear dynamic model for cables and its application to a cable-structure system[J]. Journal of Sound and Vibration, 1995, 187(4):695-712.

[2]Fujino Y, Wrnitchai W, Pacheco B M. An experimental and analytical study of autoparametric resonance in a 3DOF model of cable-stayed beam[J]. Nonlinear Dynamics, 1993, 4(4):111-138.

[3]Gattuli V, Lepidi M, John H G, Taylor A C. One-to-two global interaction in a cable-stayed beam observed through analytical finite element and experimental models[J]. International Journal of Non-linear Mechanics, 2005, 40(4): 571-588.

[4]王志搴, 趙珧冰, 孫測試, 等．索-梁組合結構的建模及面內動力特性分析.固體力學學報[J]. 2014, 35(3): 1-5.

[5]Kang Zhan, Xu Kesheng, Luo Zhen. A numerical study on nonlinear vibration of an inclined cable coupled with the deck in Cable-stayed bridges[J]. Journal of Vibration and Control,2012, 18(3): 404-416.

[5]陳水生, 孫炳楠．斜拉橋索一橋耦合非線性參數振動數值研究[J]. 土木工程學報, 2003, 36(4): 70-75.

[6]王志搴, 唐駕時, 羅迎社．索-梁耦合結構的Hopf分岔的反控制[J]. 固體力學學報, 2016, 37(1): 90-96.

[7]Zhqian Wang , Ceshe Sun, Yaobing Zhao,at al.Modeling and nonlinear modal characteristics of the cable-stayed beam[J].European Journal of Mechanics - A/Solids, 2014, 47(C)：58-69.[8]Xia Y, Fujino Y. Auto-parametric vibration of a cable-stayed beam structure under random excitation[J]. Journal of Engineering-Mechanics, 2006, 132(3): 279-286.

[9]Gattuli V, Morandini M, Paopolone A. A parametric analytical model for non-linear dynamics in cable-stayed beam[J].Earthquake Engineering and Structural Dynamics, 2002, 31(6):1281-1300.

[10]Gattuli V, Lepedi M. Nonlinear interactions in the planar dynamics of cable-stayed beam[J]. International Journal of Solid of Structures, 2003, 40(18): 4729-4748.

(責任編校：徐贊)

In-out-plane Modal Analysis of the Cable-stayed Beam

SHEN Zhong-wei
(State Grid Hunan Maintenance Company, Changsha, Hunan 410014, China)

Using the Hamilton principle and the effects of the dynamic and static configuration of the cable and beam, the equations of motion of the cable-stayed beam can be obtained. Considering the boundary and continuity conditions, the in-plane eigenvalue problem is investigated. By introducing the piecewise function, the mode shapes can be obtained. It is shown that the curve veering phenomenon can be observed in the natural frequency spectrum of the system. The frequency crossover phenomenon is obvious. Considering the local mode and global mode, the mode shapes of the cable-stayed beam are discussed.

Hamilton’s principle; cable-stayed beam; local modal

O313.3

A

10.3969/j.issn.1672-7304.2017.02.0006

1672–7304(2017)02–0025–03

2016-12-09

湖南省教育廳科研項目(15C1411)

沈忠偉(1968-)，男，湖南長沙人，工程師，主要從事電力非線性及分岔控制研究，E-mail: wangzq@hnu.edu.cn.