基于滑模觀測器的磁通切換型記憶電機永磁磁鏈辨識研究

(無錫職業技術學院，江蘇無錫， 214121)

基于滑模觀測器的磁通切換型記憶電機永磁磁鏈辨識研究

壯而行

(無錫職業技術學院，江蘇無錫， 214121)

近年來一類采用高剩磁、低矯頑力永磁材料的記憶電機得到了廣泛的研究。這類電機可以通過施加電流脈沖直接調節永磁體的磁化水平，從而大大拓寬電機的弱磁調速范圍。記憶電機在運行過程中的永磁磁鏈是可變的，僅依靠離線實驗所得的反電動勢/電流表格無法精確得出電機的磁鏈，因此需要在線觀測永磁磁鏈幅值。為此設計了基于q軸電壓方程的永磁磁鏈滑模觀測器，分析了觀測器穩定性和參數選擇依據，仿真計算證明了提出的永磁磁鏈觀測器的有效性。

磁通切換；記憶電機；永磁磁鏈辨識；滑模觀測器；仿真研究

0 引言

現代高性能永磁同步電機(Permanent Magnet Synchronous Machine, PMSM)一般采用釹鐵硼(NdFeB)永磁，具有高效率、高功率密度、結構簡單、控制方便等優點[1，2]。但是這種永磁電機的調速范圍受到電機磁鏈、電感等固有特性的限制；而且在發電運行時，故障滅磁困難，限制了其應用范圍。為了增強永磁電機的氣隙磁場調節能力，近幾年來，一類能夠通過直接改變永磁體磁化水平調節氣隙磁場的電機-記憶電機(Memory Machine， MM)，受到了國內外部分研究者的重視并取得了突破性進展。這類永磁電機采用高剩磁、低矯頑力的永磁材料，如鋁鎳鈷(AlNiCo)，可通過施加瞬時脈沖改變永磁體的磁化水平，實現氣隙磁場的調節，幾無電勵磁損耗，可以簡單高效地實現在線調磁。

記憶電機的永磁磁鏈根據運行需要是可變的，僅通過調磁電流-磁鏈關系表格無法保證調磁的正確性，因此需要加入永磁磁鏈辨識算法，與空載試驗中所得數據互相驗證。

最傳統的測量電機磁鏈的方法是在電機中埋入探測線圈，通過測量感應電動勢的方法測量電機磁鏈，但是這種方法需要改變電機的結構，可能影響電機的性能。近年來，國內外學者利用控制電機所必需測量的電流、轉速、電壓信號，采用現代控制理論和信號處理技術，觀測電機的永磁磁鏈等參數。文獻[3]利用模型參考自適應(Model Reference Adaptive System，MRSA)的方法，在使用id=0控制的情況下利用q軸電壓方程對電機參數進行了辨識。文獻采用兩步法，首先將電壓方程中的電阻值設定為設計值，再辨識轉子磁鏈。文獻[4]在采用模型參考自適應算法的基礎上，利用Popov超穩定理論設計自適應律，采用分步辨識的方法對表貼式永磁同步電機進行多參數辨識，仿真和實驗證明了該方法的有效性。文獻[5]利用擴展卡爾曼濾波(Extended Kalman Filter，EKF)的方法對電機的永磁磁鏈進行了觀測，在觀測時考慮了編碼器位置反饋誤差的影響，實驗表明該方法可以不受位置誤差的影響快速觀測永磁磁鏈。文獻[6]提出了一種自適應線性元件神經網絡法識別電機參數。該方法電機在靜止狀態時，通過注入d軸電流測得定子電阻，在電機起動過程中，將電阻設為靜止情況下的估計值，然后辨識出電機轉子磁鏈。該方法計算量小，每步迭代只需少量的加減運算，適于編程實驗。實驗驗證了該方法的可行性。文獻[7]采用量子遺傳算法對永磁電機的參數進行辨識，在辨識過程中對逆變器非線性導致的電壓畸變進行了補償，提高了辨識算法的精度。

某課題組提出將磁通切換原理與記憶電機的概念相結合，在文獻[8～9]中提出了多種不同結構的磁通切換型永磁記憶電機(Flux Switching Memory Machine, FSMM)，該類電機的鋁鎳鈷永磁體、電樞繞組和調磁繞組均位于定子上便于散熱，直流調磁繞組和電樞繞組在電氣上隔離，便于進行解耦控制。本文將以這類電機為對象，研究其調磁控制策略。

1 記憶電機的結構和數學模型

1.1 電機的結構

圖1所示為一種12/14極的磁通切換型內嵌式永磁記憶電機。其中，三相集中電樞繞組均匝繞在定子齒上，鋁鎳鈷永磁體內嵌于定子，并匝繞以直流脈沖調磁繞組。電機的磁通切換原理所示。當轉子從位置A運行到位置B時，電樞繞組匝鏈的磁鏈極性發生了交變，在運行原理上繼承了磁通切換原理，因此永磁磁鏈和相反電動勢波形也有較好的正弦性，十分適合無刷交流運行。同時，從電機運行結構可以得出，當在調磁繞組中施加瞬時正或負直流脈沖電流時，各塊永磁體將在一個電周期內被充磁或去磁到相同的磁化水平，電機有較高的調磁效率。

圖1磁通切換型內置式記憶電機的結構

圖2內嵌式結構磁通切換原理(充磁)

1.2 磁通切換型記憶電機的數學模型

為了對記憶電機進行控制，首先需建立記憶電機的數學模型。其建模方法可以比照普通磁通切換型電機[10]和混合勵磁電機[11]進行。

在兩相旋轉dq坐標系下，其磁鏈方程為

(1)

式中，id、iq—d、q軸電流；Ld、Lq、Lf—d、q軸和調磁繞組電感；Msf—調磁繞組和d軸的互感；ψpm—直軸電樞繞組所匝鏈的永磁磁鏈幅值；ψfpm—穿過調磁繞組的永磁磁鏈。在不施加調磁電流的情況下，ψpm、ψfpm—恒定不變的直流量；在調磁動態中，這兩個磁鏈值均為調磁電流的函數。

電機的電壓方程為

(2)

式中，ud、uq—dq軸下的等效電樞電壓；id、iq—dq軸下的等效電樞電流；uf—調磁繞組電壓；if—調磁繞組電流；Rs、Rf—定子和調磁繞組的電阻；ωe—電機的電角頻率。

由于調磁過程的存在，電機的動態轉矩方程比較復雜。如果調磁電流近似為梯形波，且電機dq軸電流響應較快，能很快穩定，永磁磁鏈也進入穩態，那么在調磁電流平直時，電機的電磁轉矩為電機的轉矩方程為

Te=1.5piq[ψpm+(Ld-Lq)id+Msfif]

(3)

式中，p—電機的極對數，對于FSMM即為轉子極數。

2 滑模永磁磁鏈觀測器

文中提出的永磁磁鏈辨識算法各具優勢，但也存在各自的不足之處，如擴展卡爾曼濾波法涉及矩陣運算，運算量較大；非線性自適應元件法需要選擇適當的收斂因子，否則可能會出現觀測器不收斂的情況。本章借鑒無位置控制中常用的滑模觀測器法[12]，建立基于q軸電壓方程的永磁磁鏈滑模觀測器，對不同磁化狀態下的永磁磁鏈進行辨識。

2.1 滑模觀測器原理

滑模變結構控制由前蘇聯學者Emelyanov在上世紀50年代首先提出，是一種控制表現為不連續性的非線性控制。該控制策略根據系統在動態過程中的當前狀態切換不同的系統結構，控制系統按照預定的滑動模態狀態軌跡運動。經過國內外學者的不斷研究與完善，該理論已經成為自動控制領域中的經典控制方法。

2.2 滑模變結構控制的數學描述[13]

假設有下列非線性系統

(4)

式中，x∈Rn，u∈Rn—系統的狀態向量和控制向量，控制量u=u(t,x)按以下邏輯在切換面S(t,x)=0上切換

(5)

式中，ui(t,x)、Si(t,x)—u(t,x)、S(t,x)的第i個分量；ui+(t,x)、ui-(t,x)、Si(t,x)—適當的光滑連續函數。

為使滑模變結構控制能成立，必須滿足以下滑動模態存在的充分條件。

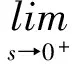
(6)

(7)

或

(8)

式(6)～式(8)既是保證滑動模態存在的充分條件，也是保證切換面外的相軌跡在有限時間內到達切換面的條件。

同等意義下的滑動條件如圖 3所示，其表達式為

(9)

(10)

圖3滑動模態到達條件

2.3dq坐標系下磁鏈觀測器的設計

滑模觀測器常用于永磁同步電機無傳感器控制中，觀測器建立于兩相靜止αβ坐標系下，通過觀測永磁磁鏈獲得轉子位置。由于本文控制的電機有轉子位置信號反饋，因此將觀測器建立在dq坐標系下，這樣永磁磁鏈僅存在于q軸方程中，且為直流量，便于濾波器的設計，可以減少抖振和觀測誤差。

忽略永磁電機的飽和與損耗時，電機在dq軸系坐標下的狀態方程為

(11)

由于永磁磁鏈只在q軸方程出現，因此將q軸方程寫為以下形式

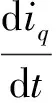
(12)

式中，A=-R/Lq,B=1/Lq,u=uq-Ldωeid，Ke=-1/Lq，eq—永磁磁鏈在q軸的旋轉電動勢。

基于式(12)，構造如下的滑模觀測器方程

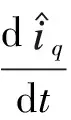
(13)

式中，符號“^”代表估計值，K—觀測器開關增益。

(14)

用式(13)減去式(12)，如果式中電機參數一致，則有

(15)

(16)

將式(15)代入式(16)得

(17)

Kgt;eq

(18)

滿足這一條件，就能產生滑模運動，誤差動態式(15)就是漸進穩定的，也保證了觀測方程的收斂。

由式(18)可知，觀測方程的收斂需要開關增益足夠大，但是過大的開關增益會造成不必要的抖振噪聲，造成估計誤差。為了充分抑制抖振，可以采用如下自適應律

(19)

式中，λ—適當選擇的大于1的常數。

當狀態點達到超平面以后，有

(20)

將式(20)代入式(15)，可以得到等效的連續輸入信號為

(21)

2.4 觀測器離散化

為了能讓觀測器能在數字系統中實現，需要對觀測器的數學模型進行離散化。設狀態空間方式形式如下

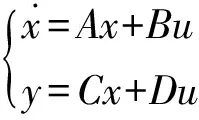
(22)

若系統的采樣周期為T，則離散時間狀態空間表達式為

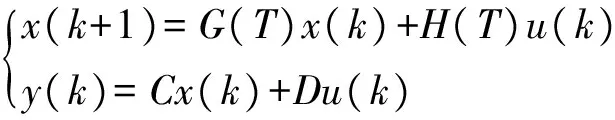
(23)

式中

(24)

當采樣周期T較小時，離散化的狀態方程可以近似表示為

x(k+1)=TAx(k)+TBu(k)

(25)

將式(13)寫成如下形式

(26)

對照式(23)～式(24)，其離散時間狀態空間表達式為

(27)

其中

(28)

3 仿真分析

根據上節提出的記憶電機磁鏈辨識策略，表1為電機參數。根據上文提出的永磁磁鏈滑模觀測器的原理，在Matlab/Simulink中搭建仿真模型如圖 4所示，其中FSMM模塊為記憶電機本體模塊，電機參數如所示通過Flux模塊的變化仿真電機在調磁狀態下永磁磁鏈的變化。

表1 電機參數

永磁磁鏈觀測器仿真模型如圖4所示。模型的輸入量為dq軸電流，d軸電壓以及電機電角速度，輸出量為永磁磁鏈在q軸的旋轉電動勢。輸出量經一階低通濾波器濾波后，除以電機電角速度，即可得觀測到的永磁磁鏈幅值。永磁磁鏈滑模觀測器模型見圖5。

圖4仿真模型

圖5永磁磁鏈滑模觀測器模型

對上述模型進行仿真，仿真場景如下：電機空載啟動，給定轉速700r/min，在0.3s時突加3 N·m轉矩；在0.5～0.6s施加調-5.5A的去磁脈沖電流，電機永磁磁鏈從0.08Wb降至0.04Wb；在0.7～0.8s施加15A的增磁脈沖電流，電機永磁磁鏈從0.04Wb增至0.08Wb，仿真所得電機磁鏈波形和觀測到的磁鏈波形見圖6，圖中點線為q軸旋轉電動勢對應的磁鏈實際值，實線為磁鏈觀測值。

從圖5中可以看出，在電機啟動階段磁鏈觀測值可以很快穩定到實際值；在0.3s突加負載時，觀測值受到擾動后很快恢復穩定；在0.5～0.6s和0.7～0.8s時，電機處于調磁階段，所觀測磁鏈為永磁磁鏈和調磁繞組產生磁鏈的疊加，在調磁動態中，觀測值也能很快跟蹤實際值。永磁磁鏈仿真波形見圖6。圖6(b)為觀測值的放大波形，波形顯示經濾波后，觀測值的抖振很小，具有較高的觀測精度。

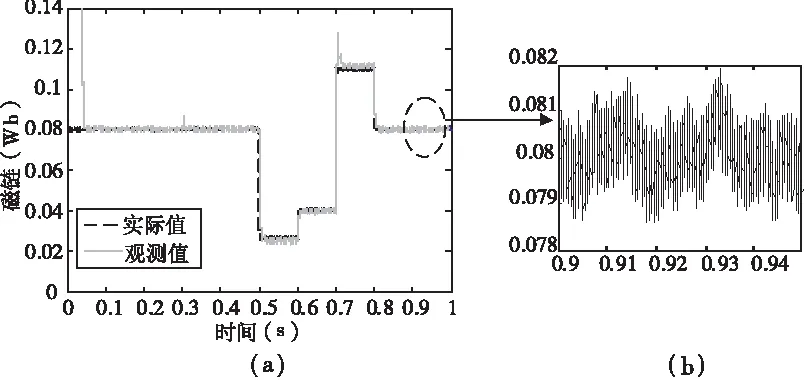
圖6永磁磁鏈仿真波形

4 結語

本文為了保證記憶電機調磁的準確性，本章提出了一種磁鏈滑模觀測器以觀測永磁磁鏈的大小；介紹了滑模觀測器的原理，基于電機q軸電壓方程建立了觀測器方程，分析了觀測器穩定性及相應的開關增益選擇原則；為方便數字實現，對觀測器進行了離散化。利用Matlab/Simulink仿真軟件搭建了觀測器的仿真模型，進行了永磁磁鏈觀測的仿真研究；仿真結果證明了所提出觀測器的可行性。

[1] 唐任遠. 現代永磁電機理論與設計[M]. 北京: 機械工業出版社, 2001, 24-32.

[2] 王秀和. 永磁電機[M]. 北京: 中國電力出版社, 2011, 21-28.

[3] Rashed M, MacConnell P F, Stronach A F,et al. Sensorless indirect-rotor-field-orientation speed control of a permanent-magnet synchronous motor with stator-resistance estimation. Industrial Electronics, IEEE Transactions on, 2007, 54(3):1664-1675.

[4] 楊宗軍, 王莉娜. 表貼式永磁同步電機的多參數在線辨識[J]. 電工技術學報,2014,(03): 111-118.

[5] 肖曦, 張猛, 李永東. 永磁同步電機永磁體狀況在線監測[J]. 中國電機工程學報,2007,(24): 43-47.

[6] 劉侃, 章兢. 基于自適應線性元件神經網絡的表面式永磁同步電機參數在線辨識[J]. 中國電機工程學報,2010,(30): 68-73.

[7] Liu K, Zhu Z Q. Quantum Genetic Algorithm Based Parameter Estimation of PMSM under Variable Speed Control Accounting for System Identifiability and VSI Nonlinearity. IEEE Transactions on Industrial Electronics, 2014:1.

[8] Yang H, Lin H, Dong J,et al. Analysis of a Novel Switched-Flux Memory Motor Employing a Time-Divisional Magnetization Strategy. IEEE Transactions on Magnetics, 2014, 50(2):849-852.

[9] Hui Y, Heyun L, Zhu Z Q,et al. Novel switched-flux hybrid permanent magnet memory machines for EV/HEV applications[C]. Electrical Machines and Systems (ICEMS), 2014 17th International Conference on, 2014:1191-1195.

[10] 賈紅云, 程明, 花為, 等. 磁通切換永磁電機等效模型與控制策略分析[J]. 電機與控制學報,2009,(05): 631-637.

[11] 楊成峰. 新型混合勵磁同步電機的分析、設計及控制策略研究[D]. 東南大學, 2007.

[12] 王成元, 夏加寬, 孫宜標. 現代電機控制技術[M]. 北京：機械工業出版社, 2009.

[13] 王豐堯. 滑模變結構控制[M]. 北京：機械工業出版社, 1998.

IdentificationResearchonPermanentMagnetFlux-LinkageofFlux-SwitchingMemoryMachineBasedonSlidingModeObserver

ZhuangErxing

(Wuxi Institute of Technology, Wuxi 214121, China)

A kind of memory machines (MMs) equipped with PM material of low coercivity and high remanence were extensively investigated recently. This kind of machines can directly adjust magnetization level of permanent magnet by applying a current pulse, thereby widely expand speed adjustment range of weak magnetic field. Since the PM flux-linkage of memory machine is variable during operation, it is hard to obtain the accurate value by back EMF/current table based on off-line experiment. Therefore, it is quite necessary to online observe the magnitude of PM flux-linkage. Therefore, a sliding mode PM flux-linkage observer based on q-axis voltage equation was designed. The operating stability and parameter selection criterion of the observer were analyzed. The simulation result proves effectiveness of the proposed PM flux-linkage observer.

Flux switching；memory machine；PM flux-linkage identification；sliding mode observer；simulation research

10.3969/J.ISSN.1008-7281.2017.06.05

TM303.3

A

1008-7281(2017)06-0014-006

壯而行男1989年生；畢業于東南大學電氣工程學院，研究方向為電機控制.

2017-06-01