晶體結構中的跨界思維
山西 劉 偉
晶體結構中的跨界思維

晶體結構與性質是選修3《物質結構與性質》模塊中的重點,而有關晶胞的計算又是重點中的難點,本部分的計算常常需要結合數學知識才能順利解答,這種跨界的考查方式令很多師生望而生畏,本文結合高考考查方向,對高考中常考到的兩種計算題型所需要儲備的知識及解題方法進行總結,以期對師生備考有所幫助。
一、考查晶體的密度
1.知識儲備
(1)單位換算:1 pm=10-12m 1 nm=10-9m
(2)晶胞質量:設晶體的化學式為XaYbZc。


(3)晶胞體積:對于平行六面體形的晶胞,晶胞的體積等于底面積乘以高。

2.題型示例
下圖是氮化鈦(TiN)的晶胞,該晶胞中N和Ti之間的最短距離為0.212 1 nm。

該氮化鈦晶體的密度為________g/cm3。(只列出算式不必計算出具體的結果,阿伏加德羅常數為6.02×1023mol-1)



二、考查晶胞參數
1.知識儲備
(1)重要的邊、角關系
②余弦定理:對于任意一個平面三角形,任何一邊的平方等于其他兩邊平方的和減去這兩邊與它們夾角余弦值的兩倍積。

c2=a2+b2-2abcosC;b2=a2+c2-2accosB;a2=b2+c2-2bccosA(公式中的參數對應上圖三角形中的參數)
③正弦定理:在任意一個平面三角形中,各邊和它所對角的正弦值的比相等。

(2)解題思路
此類試題常常讓考生計算晶胞中某線段的長度,常見的解題方法有兩種:

方法2:在晶胞中建立包含要求線段的平面三角形,利用正弦定理、余弦定理或勾股定理等數學知識解題。
2.題型示例
例1下圖是銅的晶胞實物堆積模型,設銅的密度為ρ。

則銅晶胞參數a=________cm。(只列出式子即可,阿伏加德羅常數值為6.02×1023mol-1)
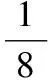

例2ZnS在熒光體、光導體材料、涂料、顏料等行業中應用廣泛,下圖為立方ZnS的晶胞,若晶胞的邊長為540.0 pm,則a位置的S2-和b位置的Zn2+之間的距離為________pm。(只列出算式即可)




山西省大同市靈丘縣豪洋中學)

