裂項相消法在數列求和中的妙用
■河南省鄭州市第一中學1903班 孫靜楠
裂項相消法在數列求和中的妙用
■河南省鄭州市第一中學1903班 孫靜楠
眾所周知,若數列{an}為等差數列,數列{bn}為等比數列,cn=anbn,求數列{cn}的前n項和時常用錯位相減法。但錯位相減法運算復雜,結果不易算對或不易化為最簡形式,為此,我們借助例題介紹用裂項相消法求這類數列的前n項和。
分析:要想用裂項相消法求數列{an}的前n項和Sn,首先應把an=(3n-1)×4n分解為另一數列相鄰兩項差的形式,即構造新數列{bn},使an=bn+1-bn,從而利用Sn=a1+a2+a3+…+an=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1。
構造數列{bn}可用待定系數法實現。
解:不設an=(3n-1)×4n=[λ(n+1)+μ]×4n+1-(λn+μ)×4n=(3λn+4λ+3μ)×4n。
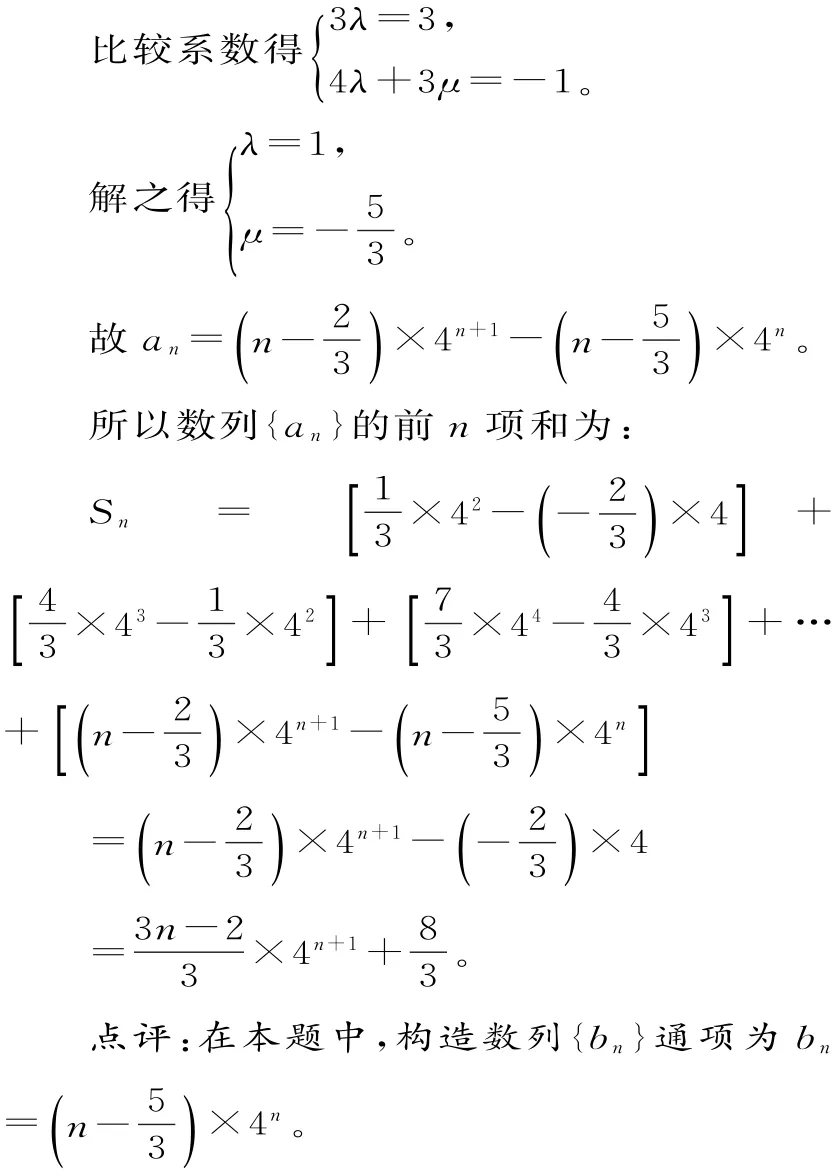
同樣,利用裂項相消也可以解決等比數列求和問題。
解:設an=a1qn-1=kqn-kqn-1=k(q-1)qn-1。令k(q-1)=a1,得
所以等比數列{an}的前n項和:
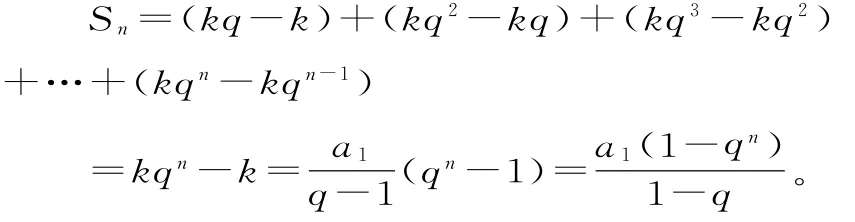
推廣:若數列{an}的通項公式為關于n的多項式,數列{bn}為等比數列,cn=anbn的前n項和的求解也可用裂項相消法。
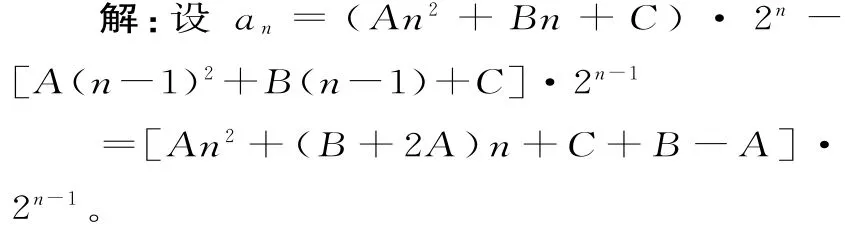
比較系數可得A=2,B+2A=0,C+B-A=0,從而A=2,B=-4,C=6。
令bn=[A(n-1)2+B(n-1)+C]·2n-1=[2(n-1)2-4(n-1)+6]·2n-1=[(n-1)2-2(n-1)+3]·2n。
所以Sn=a1+a2+a3+…+an=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1=(n2-2n+3)·2n+1-6。
從以上例題可以看出,借助待定系數法,把cn=anbn型數列(其中數列{an}的通項公式為關于n的多項式,數列{bn}為等比數列)裂項相消求和,可使計算簡單,過程簡潔,結果規范,大大降低了計算失誤的可能。
(責任編輯 徐利杰)

