基于貝葉斯網絡的智能電能表可靠性預計研究*
陳喜峰,王海濱,徐人恒,趙曉琪,李爽
(1.國網許昌供電公司,河南許昌461000;2.哈爾濱電工儀表研究所,哈爾濱150028)
0 引 言
依據國家電網建設指南規劃,預計到“十三五”時期,我國的電網建設實現全面“信息化、數字化、自動化”的智能電網工程,在該項工程中完成電能質量目標,達到電能計量的“全覆蓋、全采集”的新目標,建成用戶的用電信息采集及全費控的采集系統,對于該系統中最重要且最基礎的環節就是智能電能表[1-2]。
可靠性作為一個評判電能表的產品質量的重要指標,需要能夠進行準確的預計,來保證電能表的正常工作。電能表系統可靠性的預計方法有很多,其中包括隨機模擬方法、神經網絡法、信息融合技術法等。但是這些方法的缺點是都需要大量的樣本及輸入信息才能夠進行合理而準確的可靠性預計,所以都存在著一定的局限性[3]。
貝葉斯法能夠克服數據量小、樣本信息不足的缺陷,它是基于數理統計分析的方法,能夠借助于貝葉斯網絡中的先驗概率和后驗概率相結合形成聯合概率的雙向推理過程,實現了擴充子樣容量的效果,來彌補小子樣樣本缺陷,通過結合以往的經驗知識減少試驗的量,從而成功的實現電能表的可靠性預計。本文利用貝葉斯網絡的雙向推理特征,針對可靠性預計過程中聯合概率求解的復雜現象,引入了“桶消元法”的求解過程,進行可靠性預計的輔助計算,從而優化了電能表可靠性預計系統的性能[4]。
1 貝葉斯網絡
貝葉斯網絡起源于20世紀80年代,由圖靈獎的獲得者、美國著名學者Judea Pearl首次提出,它的核心思想是基于概率論和圖論的一種模型,模型目的為解決不定性,表示的是不確定知識的方法,它的主要特點是表達方式靈活,組織結構簡單,推理決策能力強,所以貝式網絡形式廣泛應用于人工智能、計算機科學、軟件調試、模式識別、統計決策、可靠性分析等方面,并取得了較好的成果和廣泛地應用[5]。
貝葉斯網絡其實是一種不定性的因果關聯模型,它的構成可以解讀為一種有向的無環圖例(directed acyclic graph,DAG),在圖中每一個變量對應一個節點,節點之間通過有向的實線連接,表示邏輯關系即影響概率,其中節點代表的變量可以是任何的抽象對象,例如:測試數值、故障現象、可靠性計量等等,而節點間的相互關系,可以通過條件概率來表達關系的強度,從而在已知的不確定性信息下得出推理。根據貝葉斯公式,給出如下的條件概率定義:
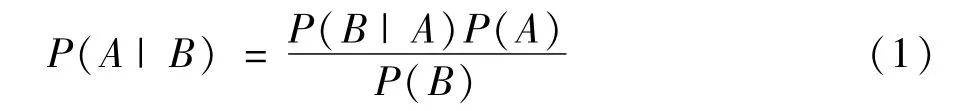
式中P(B)代表了先驗概率;P(A|B)代表了后驗概率。
貝葉斯網絡的一個重要特性是它可以實現多源信息的融合且具有雙向推理功能,即自上而下的推理也稱因果推理和自下而上的推理也稱診斷推理。在雙向推理的結構中,為了能夠直觀的表達變量的聯合概率情況和條件獨立性,總結出了鏈規則表達式如下:
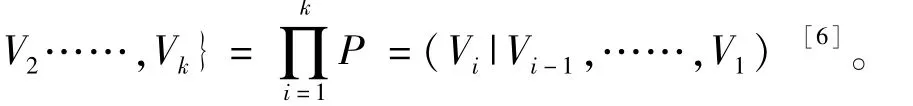
2 桶消元法
桶消元法是一種基于元素組合優化思想設計的消元方法,它能夠簡便消元過程,提升消元速度,針對系統聯合概率分布組合爆炸問題,提供較好的解決思路和方案。雖然貝葉斯網絡具有雙向推理特點,但是無論是從上至下還是從下至上均需對聯合概率求解,如針對圖 1中,已知 E1、E5,求解 P(E5,E1)的聯合概率過程。
該方法的核心思想就是利用聯合概率的鏈式乘積的規則將貝葉斯網絡圖形化得出的聯合概率分解成為一系列條件概率表的乘積形式,然后對乘積因子進行消元順序的變換,改變求和是的節點運算順序,從而減少乘積求和的運算量,最后經過整理化簡后最終公式,計算并求得結果。為了使得整個過程表述更加清晰,劃分因子區間,所以引入桶的概念,因此這個過程稱之為“桶消元法”[7]。
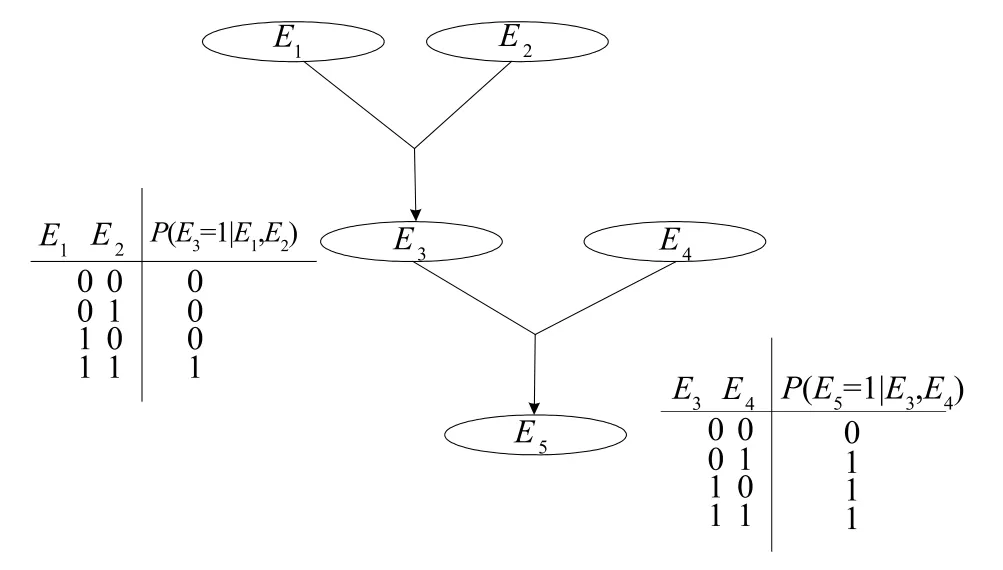
圖1 最筒單的貝葉斯網絡Fig.1 The simplest Bayesian network
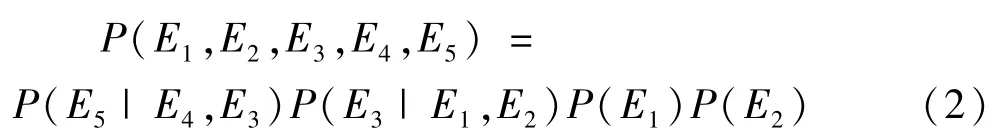
以圖1最簡單的貝葉斯網絡為例進行桶消元法的實例分析。
其中“0”代表產品正常工作狀態,“1”代表產品出現故障工作狀態,給出初始值E5=1,E1=1。求P(E5=1,E1=1)的聯合概率的桶消元過程如下:
(1)變量的初始化過程。針對每一個變量Ei生成一個Bucket[i]的桶元素,然后根據鏈規則的原理對聯合概率進行因子分解的操作,生成因子fi(i=1、2、3、4、5),如式(2)表示。得到因子函數后,將其放入到因子中最大序號的變量所對應的Bucket[i]中。例如:在式(2)中的第一個因子是 P(E5|E4,E3),其中最大序號為5,所以將該因子存放于Bucket5之中。
(2)根據已知化簡Bucket[i]中的因子函數。將已知的初值E5=1,E1=1代入所有的桶元素中,替換E5和E1,并簡化后獲得新的因子gi,然后再將得到的gi以同樣的方式再次放入因素最大序號所對應的Bucket[i]中。例如:將已知E1=1帶入到因子 P(E3|E1,E2)中,就可以獲得新的因子函數 g3=P(E3|1,E2),因子中最大序號為3,所以將新得到的g3因子放入到Bucket3中,g3和Bucket3桶中之前所存在的因子取乘運算后組成新的因子函數,P(E3|E1,E2)不再保留。
(3)計算因子函數。將Bucket[i]中的因子組合按照從大到小的順序依次計算,不斷重復第二步將組合后新的因子放入對應的最大序號的Bucket[i]中,直至所有Bucket[i]中的因子未知量全都消除。以下是具體的消元過程:
(1)第一步:將式(2)中的各因子函數放入到Bucket[i]中;
(2)第二步:將已知量E5=1和E1=1代入到各因子函數中;
(3)第三步:將每個 Bucket[i]中的因子函數執行消元操作;
(4)第四步:整理桶1中的計算結果,即:P(E5=1,E1=1)=P(E1=1)[P(E2=0)P(E4=1)+P(E2=1)]。
3 失效率
電能表的失效指的是沒有完成指定功能能力的情況。電能表的失效率是指電能表正常工作到某一時刻后,其后單位時間內的失效概率,即瞬時失效率,它能夠展示電能表某一時刻的失效速率。智能電表的失效率是指電能表在所限定的時間間隔內所出現的非人為的不可修復故障次數的累加值。
電能表失效率主要結合國際標準IEC 62059-41和GJB/Z 299C-2006《電子設備可靠性預計手冊》進行計算,也可以是來自現場使用情況的統計數據[8]。
采用元器件可靠性預計法進行預計結果時需要所用元器件種類及數量;所用元器件質量等級;設備工作環境等信息。針對可靠性模型為串聯結構的電能表[9],其失效率計算公式:

式中 λGS為設備總是效率,10-6/h;Ni為第 i種元器件的數量;λGi為第i種元器件的通用失效率,10-6/h;πQi為第i種元器件的通用質量系數;n為設備所用元器件的種類數目。
其失效率的數學定義:
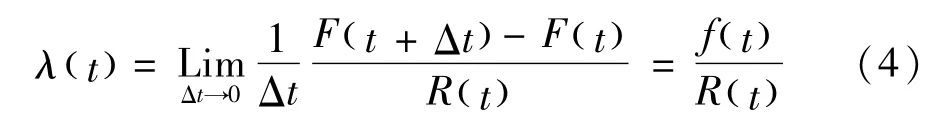
式中λ()t為瞬間失效率;F()t為分布函數;f()t為失效瞬間的概率密度;R()t為可靠性函數。
電能表及其電子元器件的失效率單位通常采用FIT(Failures In Time)表示,其含義為每十億小時內的失效數,記為1FIT=10-9/h。
4 實例分析
在電能表可靠性分析的過程中,先建立系統的故障樹(Fault Tree,FT)分析,然后將故障數模型可以直接采用映射的形式生成貝葉斯網絡。故障樹分析的過程是將系統的故障類型和原因以自上而下,由總至分的倒樹枝狀結構表示出來進行分析。下面詳細描述通過故障樹(FT)映射貝葉斯網絡(BN)模型的過程[10-11]。
BN模型是根據FT的已有結構而進行一一對應映射轉化的,轉化的關鍵在于BN是從下向上逐層分析,針對故障原因從部分至總體的樹枝狀描述,所以形成貝葉斯網絡的整個過程主要由以下幾步構成:
(1)選取貝葉斯網絡模型的節點(變量)。確定變量時將FT中的基本事件映射為BN的根節點,FT的邏輯門關系映射為BN的中間節點,區別在于FT中可能有多個相同基本事件,二BN中同一節點僅出現一次即可;
(2)根據邏輯關系形成BN的有向無環圖。有向無循環圖包括了節點和表明節點之間關系的有向弧連接線;
(3)計算各個節點(變量)的條件概率,并形成條件概率表。根據故障樹的關系可以求得貝葉斯網絡的先驗概率,同時根據故障樹的邏輯關系和已知條件計算貝葉斯網絡的條件概率表并標注于BN中,形成完整的貝葉斯網絡。
生成貝葉斯網絡之后,即可進行系統的可靠性推理,運用推理算法(即桶消元法)實現可靠性指標的計算。某單相賈控智能電能表失效的故障樹如下圖所示,圖2中給出了幾種失效模式[12-14]。
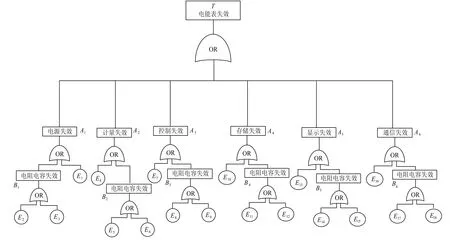
圖2 電能表失效的故障樹Fig.2 Failure tree of watt-hourmeter
根據GJB/Z 299C-2006標準的應力分析,選擇環境應力:一般地面固定,環境條件未控制;選擇電應力:依據預測產品的原理圖,通過計算、測量等方式獲得元器件在預定工作狀態下的電壓、電流、功率等電應力參數;選擇溫度應力:按工作溫度為25℃進行預計;選擇質量因子:依據元器件生產所執行的總規范和詳細規范確定。
對某型號的智能電能表施加標準的應力,按照桶消元法與貝葉斯網絡相結合計算元器件故障概率,結果如表1所示。根據上述理論,建立電能表的貝葉斯網絡如圖3所示。
則可計算出頂事件發生的概率 P(T=1)=6.277。根據GJB/Z 299C-2006標準,電能表的失效率為電源失效率、計量失效率、控制失效率、存儲失效率、顯示失效率、通信失效率之和,即:
λGS=1.136 62+2.639 03+1.123 5+0.098 8+0.130 31+1.145 05=6.273 31。
根據結果可知,失效率的偏差為0.000 589 8,通過公式計算后的結果與貝葉斯網絡推理得出的可靠性數據基本相同,所以驗證了本文提出方法的正確性。

表1 計算參數表Tab.1 Calculation of the parameter table
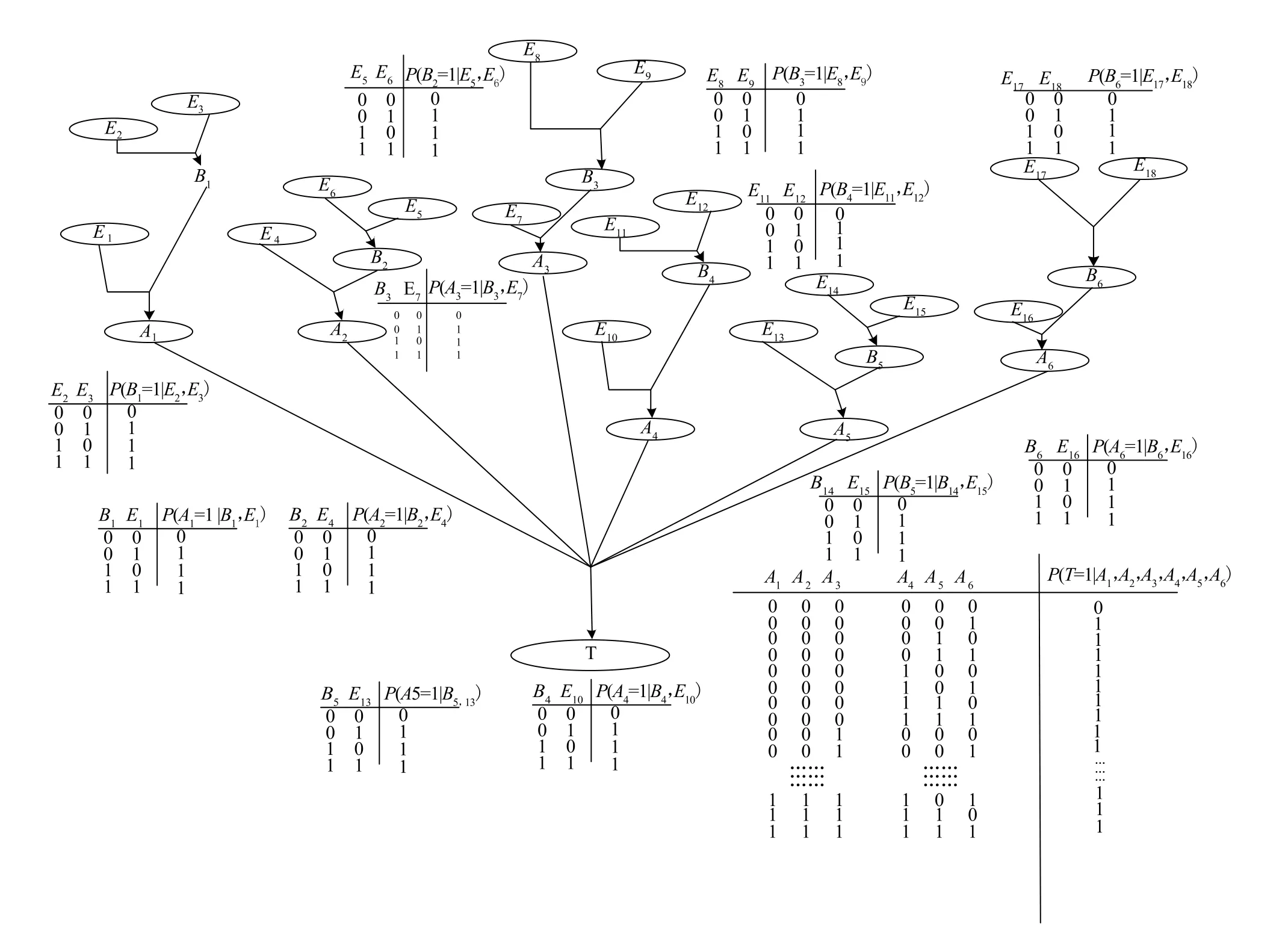
圖3 電能表的貝葉斯網絡Fig.3 Bayesian networks for watt-hourmeter
5 結束語
目前,智能電能表的產品種類繁多,電能表的行業競爭激烈,所以智能電能表的可靠性成為用戶對智能電能表選擇的關鍵因素,因此對智能電能表的可靠性研究顯得尤為重要,不僅能夠保證電力用戶的用電安全性,還能夠維護電力公司在售電方面的經濟性和合理性。
本文改進了單純依靠貝葉斯網絡對電能表的可靠性預計的傳統方法,利用了一種以貝葉斯網絡和故障樹分析相結合的思路進行可靠性預計過程,同時針對貝葉斯網絡預計過程中的復雜度進行了簡化預計的優化計算,采用了桶消元法與貝葉斯網絡相結合的新方法,在此方法下通過電能表可靠性實例驗證,得出了其可靠性預計結果與GJB/Z 299C-2006的標準里的失效率公式的計算結果的比較結論,在誤差可忽略范圍內驗證了本文所提方法的正確性和可行性。

