基于擴展相分量法的OPGW系統接地短路電流計算

鐘成，蘇漢，金志杰，杜帥兵

（1.國網河北省電力公司，石家莊050021；2.國網河北省電力公司衡水供電公司，河北衡水053000）

0 引 言

我國大部分110 kV及以上電壓等級的架空輸電線路采用雙OPGW線配置，目前的趨勢是用光纖復合OPGW線逐步代替普通地線。相較于傳統地線而言，光纖復合OPGW線阻抗值更小，故障時，短路電流通過其分流的比例更大。架空輸電線路可以分解為由檔距為單位形成的大規模電力網絡。所形成的大規模的電力網絡需要考慮的因素很多，從相導線角度來看的話，包括架空輸電線路的換位信息和線路兩側系統的參數等；從OPGW線的角度來看的話，包括OPGW是否逐塔接地運行，是否分段絕緣運行和是否經阻抗接地等多種運行方式等情形；從電力桿塔的角度來看的話，包括桿塔的級數、桿塔的型號和桿塔接地電阻等參數；進一步還包括相線和OPGW線之間、各OPGW線之間的互感影響等。這些都從一定程度上造成了線路運行狀況的復雜化［1-5］。

通過廣泛的調研發現，為了計算發生單相接地時短路電流在OPGW線上的分布，目前存在以下三種方法［6-12］：采用簡化計算方法時，沒有考慮相線和OPGW線之間的磁耦合作用，也未不考慮架空輸電線路的運行方式，OPGW線上的短路電流以線路出口變電站母線短路電流的一定百分比分流，此百分比多是基于工程經驗。此種方法雖然簡單，但是忽略的重要因素太多，導致計算結果粗糙，可信度較低。有研究者采用序分量法計算，但是序分量法應用的一個重要前提是系統的三相參數對稱，實際線路運行狀況復雜，對稱的條件更難滿足，導致計算結果保守。基于相分量的計算方法則能充分反映出輸電線路的復雜運行狀況，對三相系統參數對稱性沒有要求，導線之間的互感、架空地線的不同運行方式等因素均能體現。因此，面對線路和架空地線復雜的運行方式，相分量法在計算架空地線上短路電流的應用中越來越廣泛。文章在傳統相分量法的基礎上，并對其進行了改進，采用擴展相分量法，即將相導線和OPGW線作為一個整體，同時考慮兩者之間的相互作用，將相導線和OPGW線在分析模型上采用一致的模型來進行分析。

通過該模型對短路電流分布情況進行量化計算和EMTP算例驗證，對比驗證了文章計算結果的正確性。最后，應用文中的擴展相分量模型對某條220 kV的實際線路進行計算，得到OPGW線每級檔距上的短路電流，并總結其分布規律。這有助于實際工程中對OPGW線的選型和校驗。

1 架空輸電線路擴展相分量法模型

圖1所示為架空輸電線路的運行示意圖。圖中展示了由三相輸電導線和兩條OPGW線組成的系統。下面對圖中參數的具體含義進行逐一表述：Ea，Eb分別表示OPGW線上的感應電動勢，用Za，Zb分別表示OPGW線的自阻抗，用Ia，Ib分別表示OPGW線上的分布的電流。為了反映出OPGW線在水平方向和垂直方向上的運行方式，文章用部分有特定含義的電阻進行表示。在水平方向上，用電阻r1，r2來表示OPGW線是否處于分段絕緣的運行方式；在垂直方向上，用k1，k2來表示OPGW線在桿塔處的接地方式，具體有包括逐塔接地的方式和單點接地的方式。對r1，r2，k1，k2的值進行設置就能反映出其具體復雜的運行方式，當 r1，r2，k1，k2的值為0時，即認為連接和接地，當 r1，r2，k1，k2的值為無窮大時，即認為不連接和不接地。Fault表示發生接地短路點。

下面將介紹基于擴展相分量法的數學計算模型。將架空輸電線路的電源和線路的數學模型連接起來，并將圖1中的各級檔距上的阻抗進行矩陣化表示，就能得到完整的考慮OPGW線的架空輸電線路模型，假設線路一共有n檔，如圖2所示。

圖1 線路運行示意圖Fig.1 Schematic diagram of transmission line operation

為了方便分析，對全線上每級檔距進行編號。設定電源所在的那一級檔距為第1級，線路中的第k級檔距上的縱向電壓源用Ek來表示。用Eeq來表示線路電源的等效的電動勢矩陣。當該級檔距不是連接電源，或者該級網孔為負荷時，不難得到Ei＝0（i≠1）；當該級檔距連接的是線路的終端電源時，不難得到E1＝Eeq，Zdo＝Zeq。進一步，根據基爾霍夫電壓定律，在每級檔距上，能夠列寫出相關的網孔回路方程：

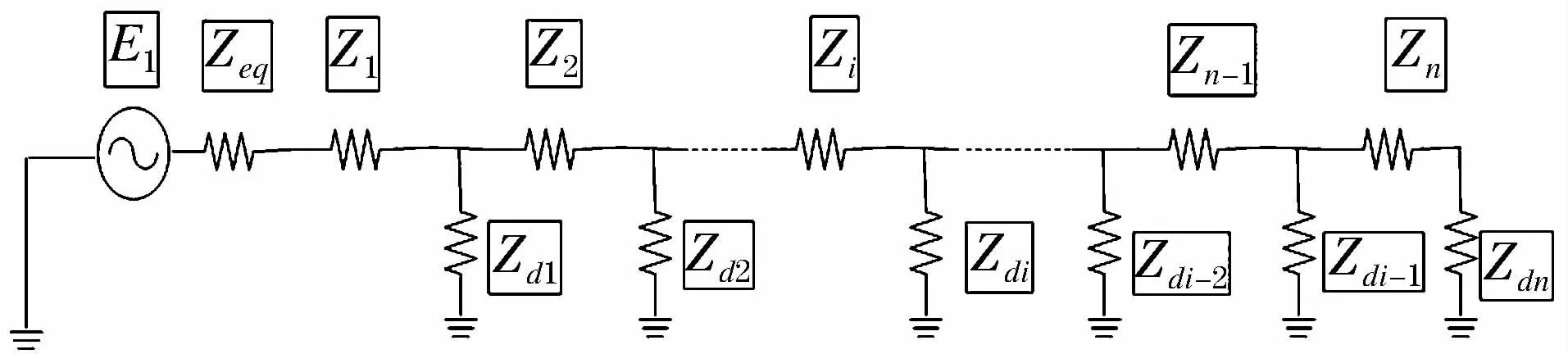
圖2 架空輸電線路擴展相分量法計算模型Fig.2 Calculation model of the improved phase componentmethod in OPGM

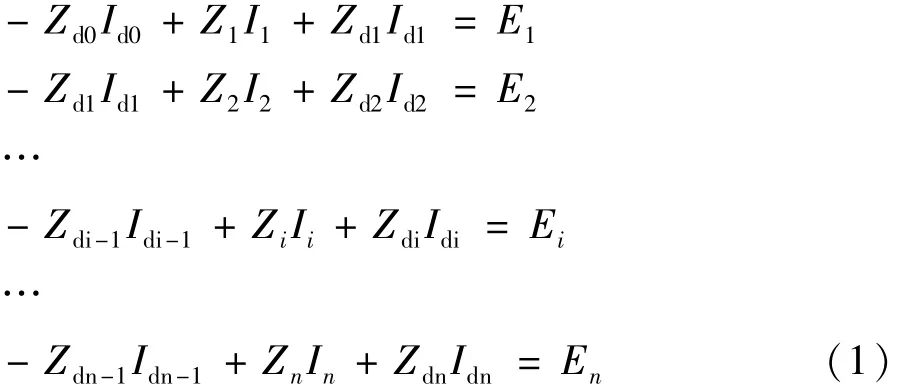
寫成矩陣：

式（2）中，I的含義為：

式（2）中，E的含義為：

下面對式（2）～式（4）中相關的矩陣進行解釋。式中I表示的是縱向電流，其中的元素Ii是一個塊矩陣。Ii的矩陣規模為y×1的列向量，是由第i級檔距上的電流組成；上式中的E表示的整條輸電線路上的縱向電壓塊矩陣。Ei的矩陣規模是大小為y×1的列向量，是由第i級檔距上的各條導線上的縱向電壓組成。需要說明的是，除了和電源相連的檔距上的縱向電壓中Ei不是一個元素全為0的矩陣，在整條輸電線路其他檔距上的縱向電壓是一個元素全為0的矩陣。

其中Z是塊三對角矩陣，即：

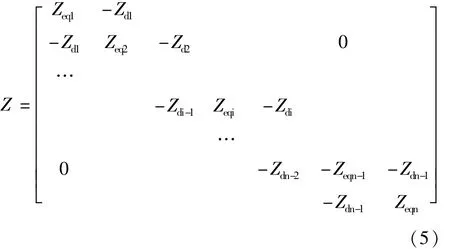
式中 Zeqi＝Zdi－1＋Zi＋Zdi（1≤i≤n）。

由以上的分析不難得到，如果整條輸電線路的檔距級數是n的話，那么Z就是一個矩陣規模為y×n的塊三角矩陣。在比較普遍的情況下，一條輸電線路的檔距級數可能在數十級甚至能夠達到數百級的規模。這時，該塊三角矩陣的階數就會是一個比較大的情況。如果使用Gauss消去法來進行處理上述方程組的話，整體的計算效率和速度都不會很快。但是可以應用“追趕法”對其進行求解。因為，該塊三角矩陣有高度稀疏，并且是對角占優的特點。

我們注意到，“追趕法”對塊三角矩陣的化簡可以很大程度上提高計算速度和計算效率，因為其對運算次數的減少效果顯著，是解決大型矩陣很好的方法［13-14］。正如上文所述，對求解文中所提到的應用擴展相分量法來計算OPGW線上短路電流分布的求解具有很好的適應度。

下面將介紹將塊三角矩陣進行“追趕法”分解的步驟，將該塊三角矩陣進行LU分解后，其中L和U的表達式如下：

式中 Gi、Di、Pi皆是 y×y階的子矩陣；Oi是 y×y階的單位矩陣。原方程可以寫成：

用待定系數法可以確定L和U中的非零元素。

式中 i＝2，3，…，n。

所以有：

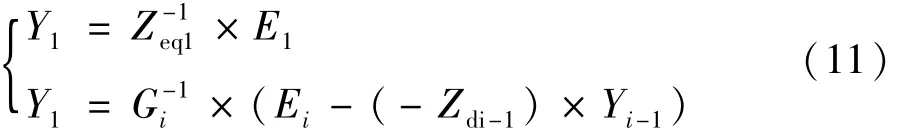
式中 i＝2，3，…，n。

再由Y＝UI求得：

式中 i＝n－1，n－2，…，1。

隨著i從1到n的變化，式（11）中Yi展示的是塊三角矩陣從小到大的求解過程，其對應著“追趕法”的“追”過程；隨著i從n到1的變化，式（12）中E′i展示的是塊三角矩陣從大到小的求解過程，其對應著“追趕法”的“趕”過程。通過上述的求解，我們不難得到：

架空輸電線路每一級檔距上的短路電流的分布都能通過以上的求解過程進行計算。

2 算例驗證

某電網110 kV單回線雙端電源輸電線路的結構示意圖如圖3所示。該架空輸電線路全線長10 km，共35級桿塔，每級檔距取平均值0.3 km，相關參數已在圖3中標示。

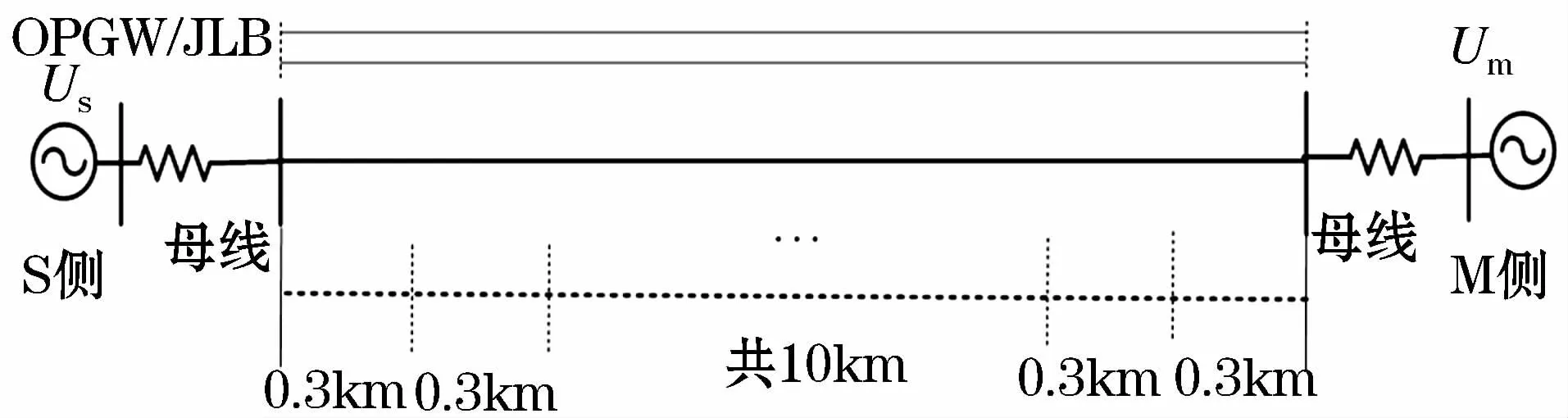
圖3 線路結構示意圖Fig.3 Structure schematic diagram of transmission line

在輸電線路發生接地短路后，故障相線上的短路電流容易得到，但是在OPGW線上的短路電流幾乎沒有進行過相關測量。為了驗證計算結果的正確性，文章將上述算例的計算結果和電力系統仿真軟件EMTP的仿真結果進行對比。EMTP是行業內認可度很高的故障分析軟件，EMTP的仿真模型中元件參數均和算例保持一致。需要說明的是，文章基于相分量模型的計算結果時故障后短路電流的穩態值，取EMTP仿真結果的穩態值與其比較，從而達到驗證的目的。

下面對建立EMTP仿真模型時的注意點進行說明。EMTP模型中的單相接地短路故障發生器由分相元件、開關和接地電阻組成，0.1 s時開關閉合，模擬A相發生接地短路，1 s后開關斷開，故障消除。這樣設置保證了足夠的時間得到發生接地短路后的電流數據，短路電流采用電流元件進行監測。LCC線路模塊能夠自定義相線和OPGW線的數目，通過對該模塊參數的設置，仿真模型中各導線之間互感的作用能夠很好地體現，1個LCC模塊表示1級檔距。圖4所示的是線路元件LCC模塊參數設置第一部分，采用5導線模型，即三相單回線和兩條OPGW線，根據算例實際情況，線路是否換位、大地電阻率、檔距長度等可在此設置。

圖4 線路LCC模塊參數設置1Fig.4 Parameter setting part of LCC 1

圖5所示的是LCC模塊參數設置第二部分，此部分影響重大。根據相線和OPGW線的型號、線路的實際塔型設置元件的參數。其中，三相導線編號依次為1～3，OPGW編號為4，JBL編號為5；Rout表示導線的半徑；Resis表示導線單位長度的直流電阻值；Horiz表示以中間相為參考時的水平距離；Vtower表示導線在桿塔處的垂直距離；Vmid表示導線在檔距中央是的垂直距離；Separ表示分裂導線之間的距離；NB表示導線分裂數。為保證仿真結果的準確性，所有的參數均需進行正確的設置。點擊View后能夠對設置的塔型進行預覽，頂部是兩條OPGW線，下方是三條相導線，同時和塔型CAD圖進行校準。每檔的OPGW線和相線上的電流均采用電流元件進行監測，采集故障后的數據。

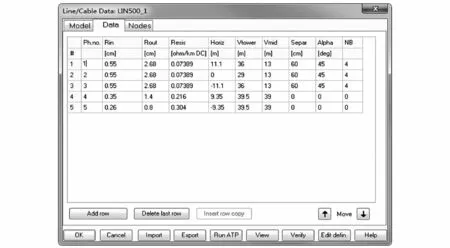
圖5 線路LCC模塊參數設置2Fig.5 Parameter setting part of LCC 2

當在輸電線路的中部5 km，即18號檔距處發生單相接地短路時，A相的短路電流計算結果如表1所示，短路點的短路電流由兩端電源提供，分別見表1中的S側提供的短路電流和M側提供的短路電流。從表1中能夠看出，對于本算例中的雙端電源線路，EMTP仿真結果和文中計算結果在一個比較理想的范圍內，相差0.5%左右。說明了基于文中計算方法得到的相線上接地短路電流的分布是可靠的。

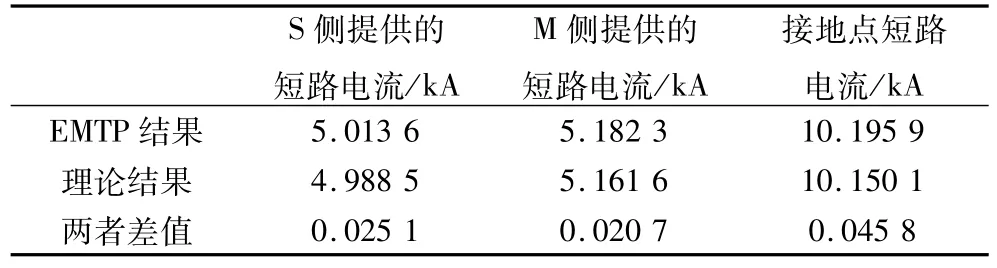
表1 單相接地短路電流的比較Tab.1 Comparison of single-phase to ground fault current

進一步對OPGW線上的電流分布情況進行驗證，由于OPGW線的逐塔接地，使得全線每級檔距段的OPGW線上電流值也不相同。表2表示仿真和文中計算得到的光纖復合OPGW線OPGW和普通OPGW線JLB上短路電流。

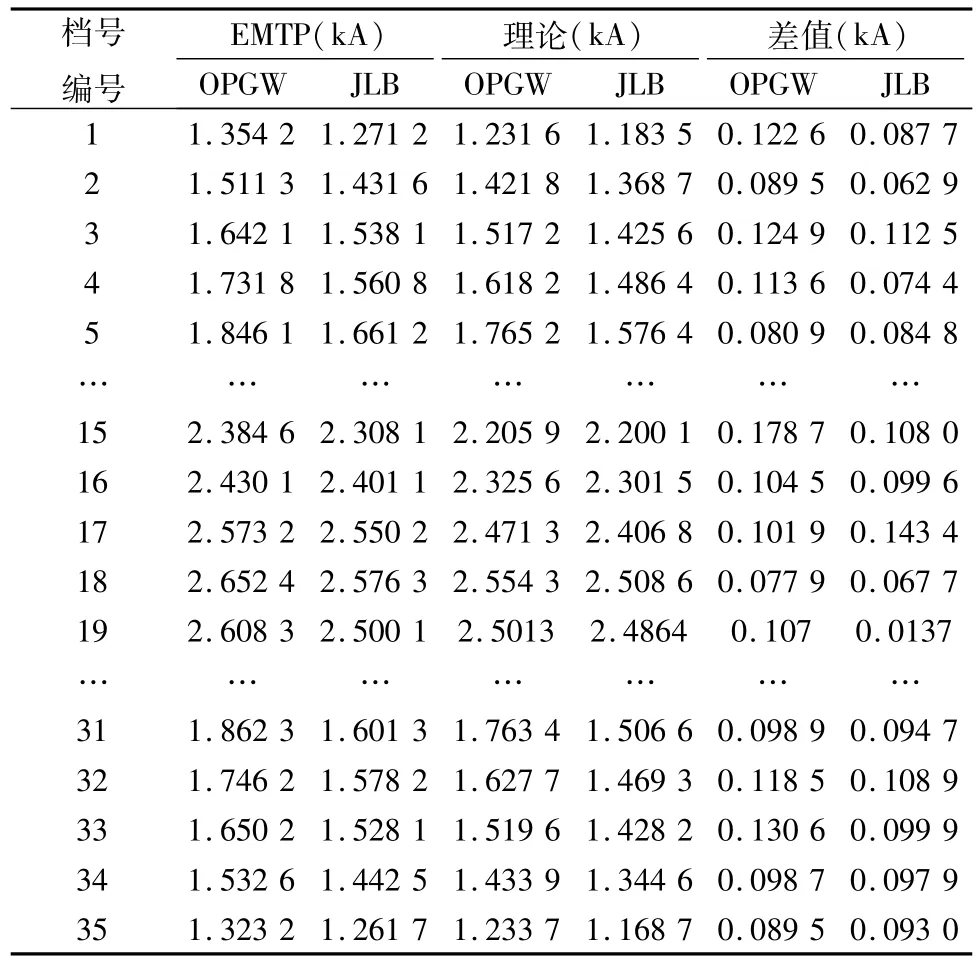
表2 OPGW和JLB每檔上電流的比較Tab.2 The comparison of current on OPGW and JLB

通過對OPGW線和JLB兩條OPGW線，EMTP和計算結果的對比發現：在發生短路的18號檔距處，檔距上的短路電流相差不大，差值分別為0.077 9 kA和0.067 7 kA。隨著從短路點到線路首末兩端檔距的推移，仿真結果和計算結果的差值變大，但在可接受的范圍內。兩者誤差產生的原因在于計算時兩條OPGW線之間的互感影響也考慮了進來，但在LCC模塊中只有相線對OPGW線的影響。注意到，在短路點附近檔距上導線短路電流是全線檔距中最大的，對OPGW線的挑戰最為嚴峻，和EMTP仿真差別不大可說明文章提出的計算方法得到的結果是可靠的。綜合以上分析，EMTP仿真結果和文中的計算結果在相線和OPGW線上短路電流的分布情況都有很好的吻合，從而驗證了文章算法的正確性。

需要說明的是，若只用EMTP進行仿真，面對輸電線路的幾十級甚至上百級桿塔，需要對每級桿塔和各導線參數都要進行繁瑣的設置，才能得到準確的仿真結果，計算時間和成本不容忽視［15］。依托文中計算方法的而開發架空輸電線路單相接地短路電氣量分布計算軟件，計算中可設定塔型后調用，和EMTP相比較，計算效率顯著提升，并已在相關工程項目中應用。

3 實際線路上的應用

某110 kV線路單回線運行，線路長度為7.8 km，導線為 JL/G1A-400/35-48/7鋼芯鋁絞線，單位長度電抗為0.416Ω/km，架空地線為OPGW-24B1-100，OPGW線電抗為0.216Ω/km。

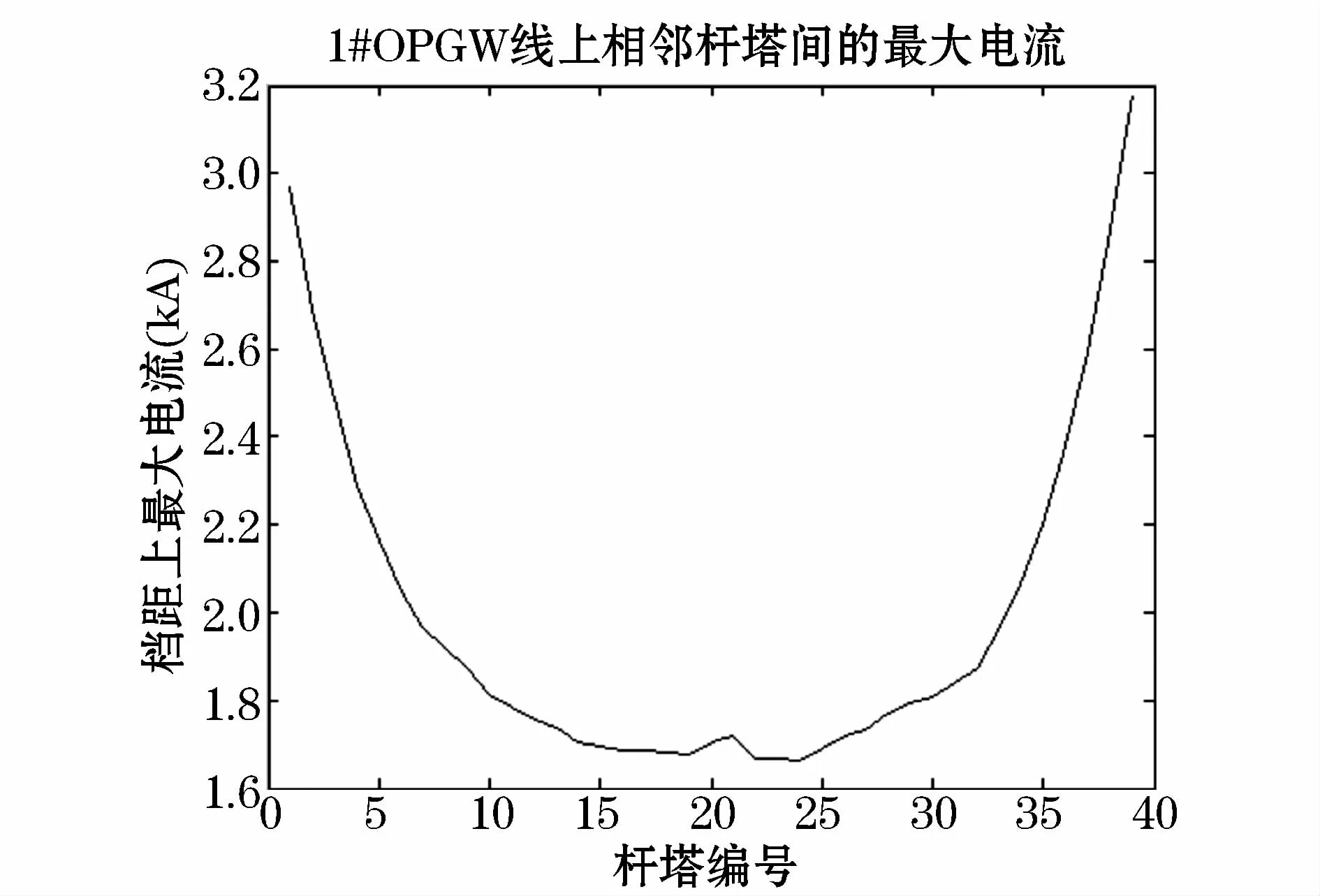
圖6 線路逐塔短路時1＃OPGW線上電流分布Fig.6 Fault current distribution on OPGW1

逐塔故障時，1＃OPGW線上的最大電流分布如圖6所示，2＃OPGW線上的最大電流分布如圖7所示。根據圖6和圖7，可以對OPGW線上短路電流的分布情況進行分析。隨著發生接地短路的桿塔從線路首端向線路末端變化，OPGW線上最大短路電流也逐漸經歷從一個最大值向最小值分布的過程。這與線路兩端電源的供流有關，同時在發生接地短路的桿塔處的相鄰檔距上OPGW線的短路電流必然最大，在此處應考慮對OPGW線的分流水平。對每一級檔距OPGW線短路電流的校驗需要重點考慮與該級檔距相連的桿塔處發生接地短路，此種狀況是考驗最為嚴峻的情形。

圖7 逐塔短路時2＃OPGW線上電流分布Fig.7 The fault current distribution on OPGW2

4 結束語

文章針對架空輸電系統的單相接地短路故障，充分考慮了三相導線和雙OPGW線的復雜運行方式，更適用于雙端電源、雙OPGW線和多相線配置的輸電線路上發生單相接地短路時，短路電流在OPGW線中的分布計算。利用上述方法，也能計算出發生單相接地短路時，OPGW線的分流系數。基于文中方法而開發出的計算軟件，已經在實際工程中應用，取得了良好的工程效應，能夠得出文章的研究內容在變電站設計，輸電線路的建設等工程實際中有重要意義的結論。