臺階地形爆破振動放大與衰減效應研究＊

武 旭，張云鵬，郭奇峰

臺階地形爆破振動放大與衰減效應研究＊

武 旭1，2，張云鵬3，郭奇峰1，2

（1.北京科技大學土木與資源工程學院，北京100083；2.北京科技大學金屬礦山高效開采與安全教育部重點實驗室，北京100083；3.華北理工大學礦業工程學院，河北 唐山063009）

基于臺階地形爆破振動數值模擬與邊坡振動監測實驗，研究臺階地形爆破振動速度在傳播過程中高程放大效應的產生及變化規律。結果表明，單個臺階坡頂質點的振動速度放大效應是在距爆源一定距離、達到一定高差的條件下產生的；坡頂質點振動速度放大倍數并不隨臺階高度的增加而單調增加，在臺階高度超過某一臨界值后，放大倍數隨臺階高度的增加而減小。臺階高程對爆破振動速度既有放大作用，同時也隨高度的增加產生衰減作用。根據模擬計算及現場觀測數據分析結果，給出了臺階地形爆破振動速度預測模型，該模型為類似邊坡工程的爆破地震波傳播規律研究提供一定的參考。

臺階地形；高程差；爆破振動；放大效應

爆破振動強度的影響因素極其復雜，其衰減特征是在基于實踐經驗和對數據統計分析的基礎上得到的，隨著爆破技術在邊坡工程中的廣泛應用，薩道夫斯基公式計算值與實測數據的誤差達到50%以上［1］，該公式對高差變化較大的地形已不再適用。許多學者采用現場實驗、理論分析及數值模擬等手段對爆破振動的地形效應進行了深入研究。臺階地形的放大效應與高程、爆源距、坡面角以及結構面的產狀有關［2－5］。呂淑然等［6］認為臺階正高差地形的高程越高放大效應越明顯，而唐海等［1］認為臺階地形中振動速度的放大系數存在最大值。萬鵬鵬等［7］通過實驗觀測分析得到臺階地形爆破振動放大效應是受鞭梢效應和坡面效應影響的結論。張偉康等［8］、胡光球等［9］、周同齡等［10］通過分析與爆破振動有關的物理量，運用量綱分析法推導了反映高程放大效應的爆破振動公式并在工程中應用。同時，動力有限元方法成功應用在了爆破動態模擬中，并被證明在邊坡頂部質點振動速度都呈現出放大效應［11］，放大現象是一個局部的動力響應［12］，振動速度放大效應的實質是在臺階平臺上產生波形轉換及波形疊加［13］。

本文中利用數值模擬方法對臺階地形爆破地震波的放大與衰減規律進行研究，結合現場實驗數據分析結果提出臺階地形爆破振動速度預測模型。

1 數值模擬

1.1 參數選取

模型做如下假設：巖石視為各向同性的連續均勻介質，爆轟產物的膨脹是絕熱過程；忽略重力影響。臺階模型的巖石材料參數如表1所示，炸藥材料及狀態方程參數如表2所示。

表1 巖石材料參數Table 1Material parameters of rock

表2 炸藥的材料和狀態方程參數Table 2Material and equation of state parameters of explosive

采用高能炸藥材料和JWL狀態方程描述，爆轟壓力計算：

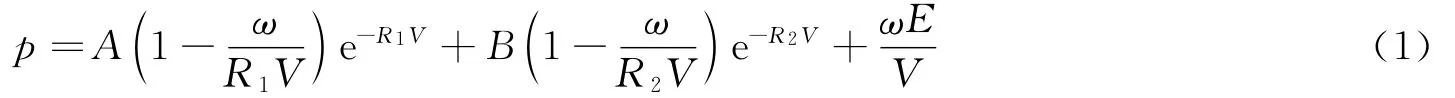
式中：p為爆轟壓力，E為炸藥爆轟產物的內能，V 為爆轟產物的相對體積，A、B、R1、R2、ω、為所選炸藥的性質常數。

1.2 模型建立

利用LS－DYNA程序建立爆破模型，根據實驗方案、巖石物理力學參數以及爆破參數，邊坡爆破各模型尺寸：臺階高度H 分別為12、15、18、21m；臺階坡底面寬度W 分別為10、15、20m；坡面角為90°。圖1中給出了模型邊界條件及炮孔主要參數。

1.3 臺階高度對振速的影響

模型計算時間0.03s。爆炸后模型質點豎直方向振動速度隨時間變化形態如圖2所示。

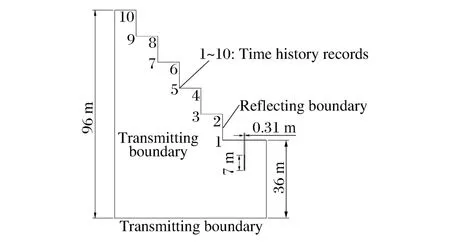
圖1 計算模型示意圖Fig.1Sketch map of calculation model

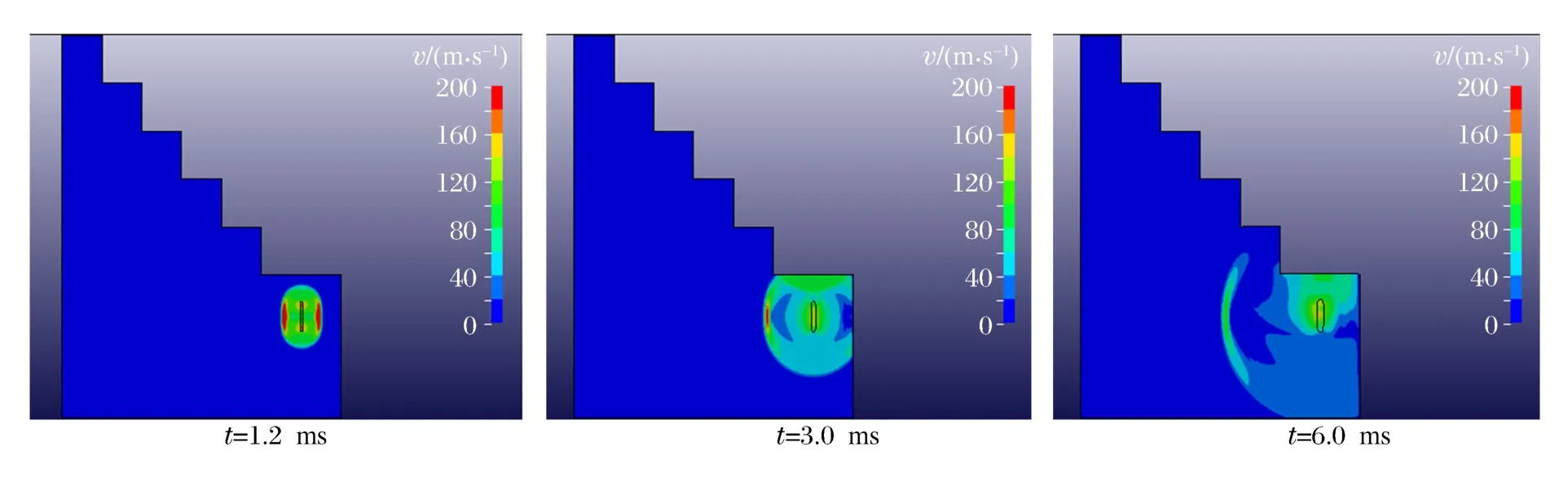
圖2 振動速度云圖Fig.2Vibration velocity nephogram

通過LS－PrePost后處理程序提取時間歷程記錄點處豎直方向的峰值質點振動速度，12組數值模型的計算結果如圖3所示。

圖3 質點峰值振動速度隨高程變化曲線Fig.3Variation of peak particle vibration velocity with elevation

臺階表面質點振動速度總體上隨距離的增加呈指數衰減規律；對于單個臺階，由于高差的存在質點振動速度在上級臺階坡頂處產生放大效應。由圖2中曲線分析可得：爆破振動速度的高程放大效應是在爆源距和高差達到一定值后產生。當W＝10m、H＝12m，振動速度的放大效應在第3級臺階出現，為研究產生放大效應后高程對振動速度的影響規律，改變第3級臺階的高度，建立16個臺階模型。

臺階坡頂質點振動速度的放大倍數n隨高差的變化曲線如圖4所示，高差由1m增加到18m，放大倍數n呈現先增加后降低的變化規律，當高差為9m時，放大倍數n達到最大值1.34。

質點振動速度的放大倍數并不隨臺階高度的增加而單調增加，當臺階高度超過某一臨界值時，放大倍數隨臺階高度的增加而減小。這一現象表明，高程對地震波既有放大作用也存在衰減作用。

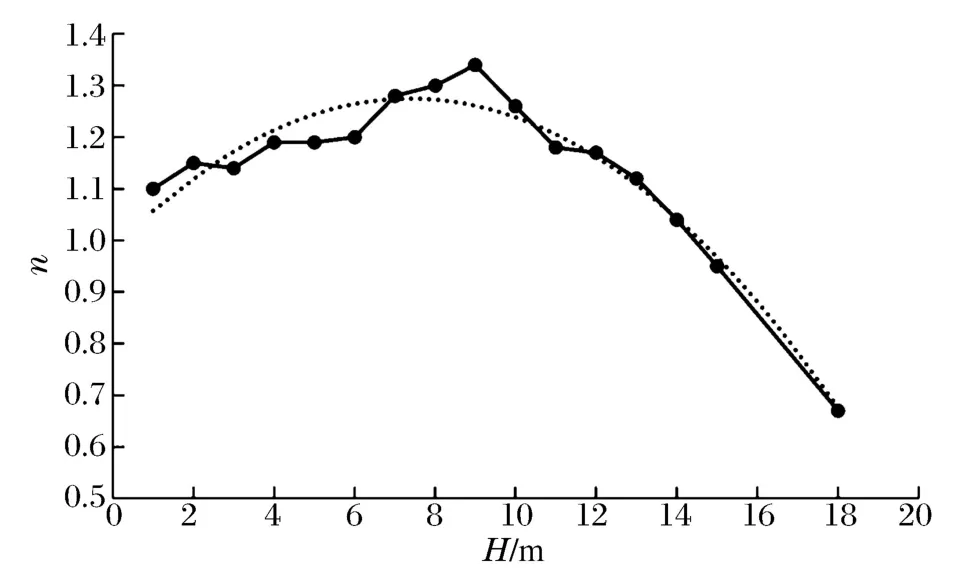
圖4 放大倍數隨高程變化曲線Fig.4Variation of amplification factor with elevation

1.4 臺階坡底面寬度對振速的影響

當臺階高度一定，坡底面寬度分別為10、15、20m時，建立12組數值模型，臺階坡頂、坡底處質點峰值振動速度與坡底面寬度的關系如圖5所示。

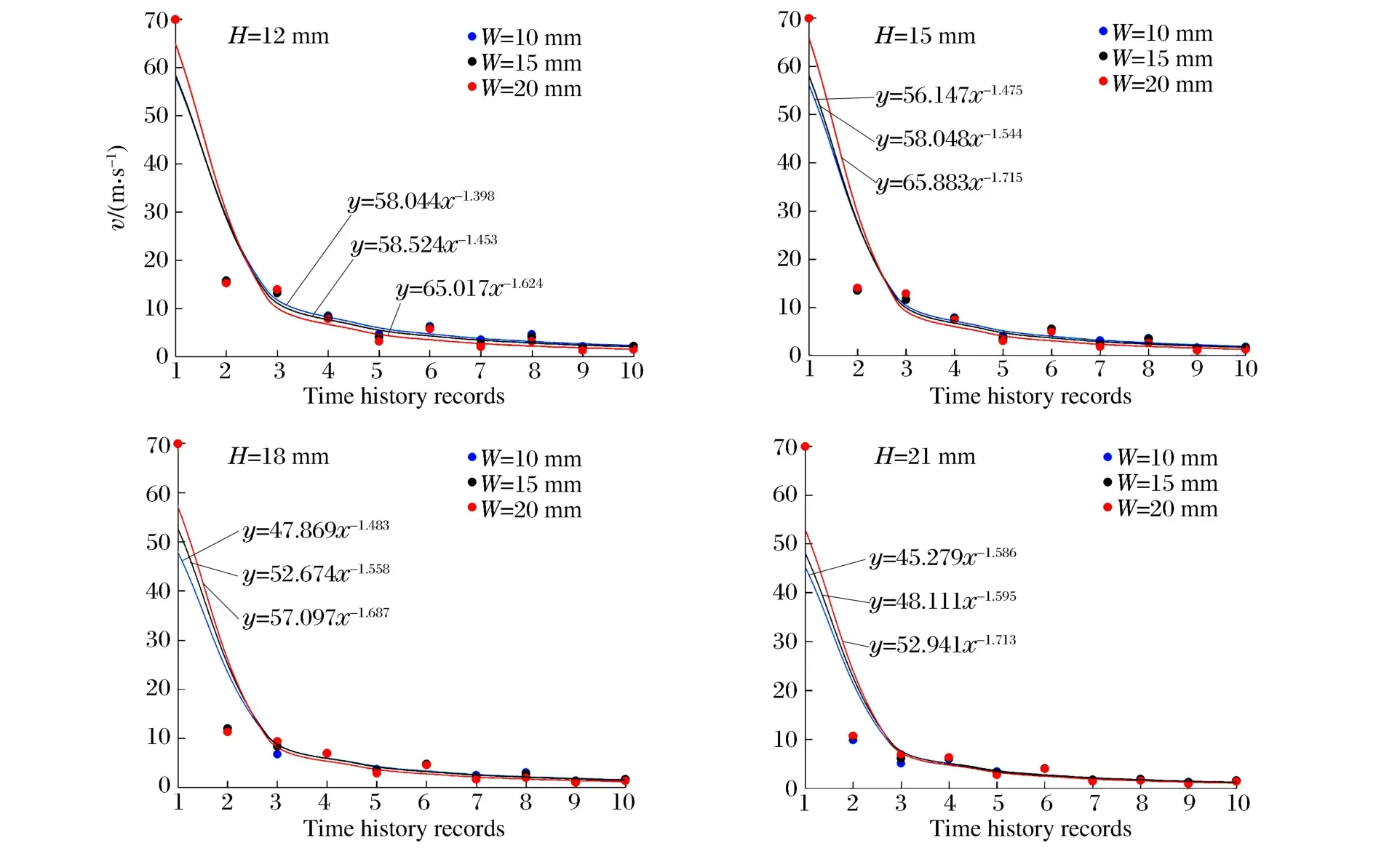
圖5振動速度與坡底面寬度的關系Fig.5Relation of bottom width with vibration velocity

圖4 中質點峰值振動速度衰減特征顯示，坡底面寬度越大，相同高程處質點振動速度越低；坡底面寬度較大臺階的爆破振動速度衰減速率更快。振動速度隨坡面寬度增大而減小。在有高差存在的臺階地形中，高程和爆源水平距離的共同作用影響爆破振動速度的大小。

2 反應高程的數學模型

根據模擬實驗數據的分析結果，結合對各參考文獻中爆破振動速度計算經驗公式的分析，認為用下式對臺階地形爆破振動速度計算更為準確：

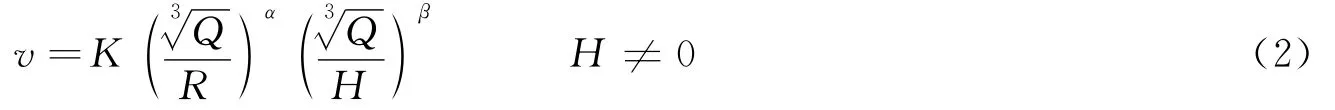
式中：v為質點峰值振動速度，Q為裝藥量，R為距爆源的水平距離，H 為高程差，K、α、β為與巖石、地形相關的系數。

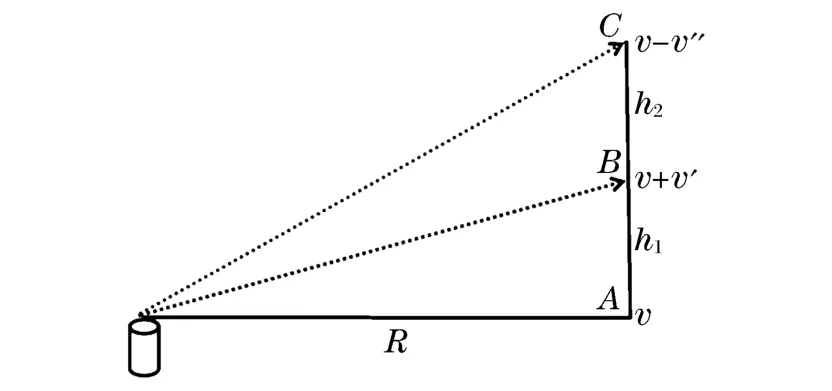
圖6 高程對振速的放大與衰減示意圖Fig.6Amplification and attenuation of vibration velocity based on elevation

如圖6所示，炸藥爆炸后產生的爆破地震波傳播至點A、B、C時，水平距離R對振動速度的衰減作用相同，A點振動速度為v，由于高程的影響B點振速為v＋v′，高差h1對振動速度起到放大作用；當單個臺階高程增加為h1＋h2時，C點速度降為v－v″，此時高程對振動速度起到衰減的作用。式（2）中R為距爆源水平距離，不影響高差對振速的作用。高差H 值在一定范圍內，產生振速放大效應，數據擬合得到的β為負值；高程增加到某一值后，此時速度v隨著H 的不斷增加而降低，數據擬合得到的β為正值。

3 工程實例

露天深孔爆破炮孔直徑310mm，孔深14～17.5m，超深2～2.5m，填塞長度7～8m，孔網參數：礦石a×b＝（7～8）m×（6～7）m，巖石a×b＝（5～9）m×（4～8）m。露天臺階高度12～15m。

爆破振動監測工作采用TC－4850爆破測振儀，如圖7所示。布置8個測點采集各臺階坡底和坡頂質點振動速度，測點位置如圖8所示。

圖7 爆破振動速度現場監測Fig.7Field monitoring of blasting vibration velocity

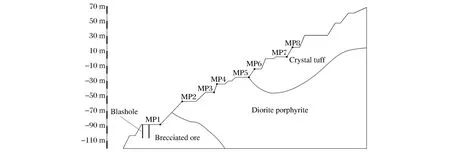
圖8 測點布置臺階剖面圖Fig.8Arrangement of measuring points

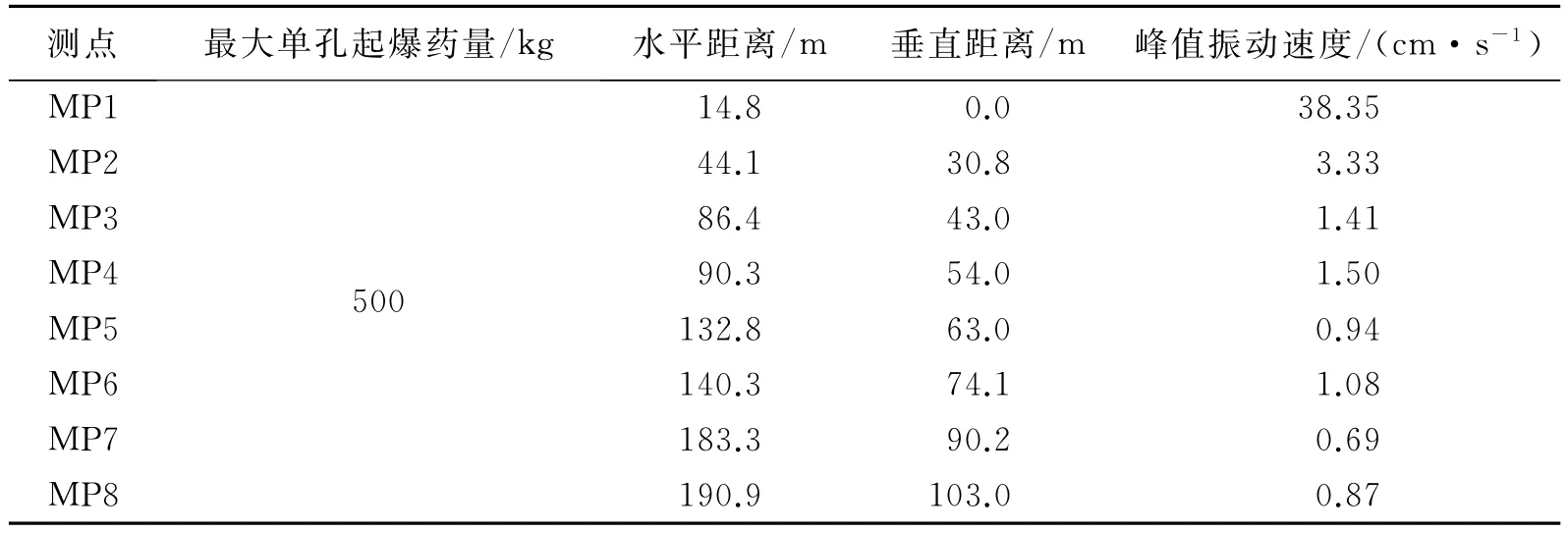
表3 爆破振動觀測結果Table 3Blasting vibration measurements

從表3數據可知，測點4、6和8均出現振動速度放大現象，根據公式（2）進行數據擬合處理得：

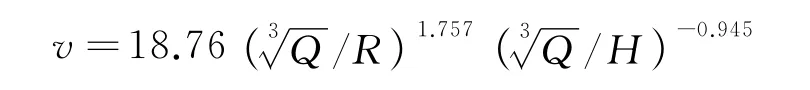
相關系數r2＝0.995 3；撒道夫斯基公式擬合相關系數為0.945 3，相關性與公式（2）相比較低，且不能直觀體現地形高差對爆破振動速度的影響。

4 結 論

（1）臺階表面質點振動速度隨著距離的增加整體上呈指數衰減規律；對于單個臺階，由于高差的存在坡頂質點產生振動速度放大效應，放大效應在距爆源一定距離、達到一定高差的條件下產生。

（2）坡頂質點振動速度放大倍數并不隨臺階高度的增加而單調增加，臺階高度超過某一臨界值后，放大倍數隨臺階高度的增加而減小。

（3）坡底面寬度越大，爆破振動速度衰減速率越快，相同高程處質點振動速度越小。

［1］ 唐海，李海波.反映高程放大效應的爆破振動公式研究［J］.巖土力學，2011，32（3）：820－824.Tang Hai，Li Haibo.Study of blasting vibration formula of reflecting amplification effect on elevation［J］.Rock and Soil Mechanics，2011，32（3）：820－824.

［2］ 朱傳統，劉宏根.地震波參數沿邊坡坡面傳播規律公式選擇［J］.爆破，1988，5（2）：30－34.Zhu Chuantong，Liu Honggen.Selection of formula on propagation of the parameters of explosive seismic wave along slope［J］.Blasting，1988，5（2）：30－34.

［3］ 王在泉，陸文興.高邊坡爆破開挖震動傳播規律及質量控制［J］.爆破，1994，11（3）：1－4.Wang Zaiquan，Lu Wenxing.Propagation of blasting vibration and quality control of high slope in excavation by blast［J］.Blasting，1994，11（3）：1－4.

［4］ 舒大強，何蘊龍，董振華.巖質高邊坡開挖爆破震動荷載及其對邊坡穩定性影響的研究［J］.工程爆破，1996，2（4）：39－43.Shu Daqiang，He Yunlong，Dong Zhenhua.Research on vibration load from excavation blasting and its influence on stability of rock high－slope［J］.Engineering Blasting，1996，2（4）：39－43.

［5］ 舒大強，李小聯，占學軍，等.龍灘水電工程右岸高邊坡開挖爆破震動觀測與分析［J］.爆破，2002，19（4）：65－67.Shu Daqiang，Li Xiaolian，Zhan Xuejun，et al.Observation and analysis of blasting vibration on the right bank’s high slope of Longtan hydropower project［J］.Blasting，2002，19（4）：65－67.

［6］ 呂淑然，楊軍.露天礦爆破地震效應與降震技術研究［J］.有色金屬，2003，55（3）：30－32.LüShuran，Yang Jun.Study on blasting seismic effect and anti－vibration technology in the open－pit mine［J］.Non－ferrous Metal，2003，55（3）：30－32.

［7］ 萬鵬鵬，璩世杰，許文耀，等.臺階爆破質點振速的高程效應研究［J］.爆破，2015，32（2）：29－32.Wan Pengpeng，Qu Shijie，Xu Wenyao，et al.Study of elevation effect of bench blasting particle vibration velocity［J］.Blasting，2015，32（2）：29－32.

［8］ 張偉康，謝永生，吳順川，等.礦山邊坡爆破振動高程放大效應研究［J］.金屬礦山，2015，44（3）：68－71.Zhang Weikang，Xie Yongsheng，Wu Shunchuan，et al.Research on elevation amplification effect of blasting vibration in mine slope［J］.Metal Mine，2015，44（3）：68－71.

［9］ 胡光球，璩世杰，梁新民.高程放大效應對露天采場爆破震動衰減的影響研究［J］.黃金，2015，36（7）：28－32.Hu Guangqiu，Qu Shijie，Liang Xinmin.Research on the influence of elevation amplification effect on open－pit blasting vibration attenuation［J］.Gold，2015，36（7）：28－32.

［10］ 周同齡，李玉壽.反映高程的爆破震動公式及其應用［J］.江蘇煤炭，1997，22（4）：21－22.Zhou Tongling，Li Yushou.Blasting vibration formula of reflecting amplification and application［J］.Jiangsu Coal，1997，22（4）：21－22.

［11］ 付波，胡英國，盧文波，等.巖石高邊坡爆破振動局部放大效應分析［J］.爆破，2014，31（2）：1－7.Fu Bo，Hu Yingguo，Lu Wenbo，et al.Local amplification effect of blasting vibration in high rock slope［J］.Blasting，2014，31（2）：1－7.

［12］ 林士炎，李長洪，喬蘭，等.爆破震動對高速路邊坡影響的數值模擬［J］.北京科技大學學報，2003，25（6）：507－509.Lin Shiyan，Li Changhong，Qiao Lan，et al.Numerical simulation on the influence of blasting vibration on the freeway slope［J］.Journal of University of Science and Technology Beijing，2003，25（6）：507－509.

［13］ 李山有，馬強，韋慶海.地震體波斜入射下的斷層臺階地震反應分析［J］.地震研究，2005，28（3）：277－281.Li Shanyou，Ma Qiang，Wei Qinghai.Seismic response analysis of fault step subjected to obliquely incident body waves［J］.Journal of Seismological Research，2005，28（3）：277－281.

Amplification and attenuation effect of blasting vibration on step topography

Wu Xu1，2，Zhang Yunpeng3，Guo Qifeng1，2
（1.School of Civil and Environmental Engineering，University of Science and Technology Beijing，Beijing100083，China；2.Key Laboratory of High－Efficient Mining and Safety of Metal Mines，University of Science and Technology Beijing，Beijing100083，China；3.College of Mining Engineering，North China University of Science and Technology，Tangshan 063009，Hebei，China）

The present study investigates the growth and variation of the amplification effect in the propagation of the blasting vibration velocity in step topography.The results indicate that the blast vibration elevation amplification effect on a single step occurs at a certain distance and elevation；the peak particle velocity magnification of the top of the slope doesn’t increase monotonously with the increase of the elevation；and the magnification decreases when the elevation exceeds a certain critical value.The elevation exerts an effect of both amplification and attenuation on the blasting vibration velocity.According to the data analysis of the numerical simulation and the field experiment，a model of the blasting vibration velocity prediction on step topography was presented，providing reference for the research of blasting seismic wave propagation law in similar slope projects.

step topography；elevation difference；blasting vibration；amplification effect

O389 國標學科代碼：13035

A

10.11883／1001－1455（2017）06－1017－06

2016－03－29；

2016－07－29

國家自然科學基金項目（51604017）；中央高校基本科研業務費專項基金項目（FRF－TP－16－017A3）

武 旭（1988— ），男，博士，13051510807＠163.com。

（責任編輯 曾月蓉）