具有分數階阻尼的波動方程的吸引子的正則性

韓英豪， 田雨嘉， 劉 爽， 楊玉彤

(遼寧師范大學 數學學院，遼寧 大連 116029)

具有分數階阻尼的波動方程的吸引子的正則性

韓英豪， 田雨嘉， 劉 爽， 楊玉彤

(遼寧師范大學 數學學院，遼寧 大連 116029)

研究了具有分數階衰減項的半線性波動方程解的漸近正則性.當非線性項滿足臨界增長率時，韓英豪等人證明了上述方程相關聯的半群在相空間H0中具有整體吸引子A.對外力項f和非線性項φ附加一些條件下可以證明上述半群在相空間H1中具有整體吸引子A1．顯然，A1?A.如果可以證明A是H1的有界集，那么由整體吸引子的極大性，反過來的包含關系就成立．但一般情況下，僅僅假設f∈H-1(Ω)，不能證明A在H1中的有界性．對f和φ施加適當的假設條件下證明了A在H1中的有界性．

漸近正則性；分數階衰減；半線性波動方程

研究如下具有分數階衰減項的半線性波動方程的漸近正則性：

utt+ω(-Δ)θut-Δu+φ(u)=f,x∈Ω,t≥0.

(1)

其中，Ω?3是有界立方體．即，存在L1,L2,L3>0，使得而θ∈(0,1],ω>0是給定參數．未知函數u=u(x,t)滿足初始條件

u(x,0)=u0(x),ut(x,0)=u1(x),x∈Ω

和周期邊界條件

其中，Γj=Γ∩{xj=0},Γj+3=Γ∩{xj=Lj},j=1,2,3,f為外力項，φ為非線性項．

對此類方程有一些學者進行過研究．在文獻[1]中對上述方程研究了局部解的存在性，在文獻[2-3]中研究了漸近行為，在文獻[4-6]中證明了吸引子的存在性．

文獻[4]中對外力項f(x)給出了如下條件:

f(x)∈H-1(Ω).

(2)

對非線性項φ∈C()給出了如下條件：

存在c>0,對任意r,s∈，滿足

|φ(r)-φ(s)|≤c|r-s|(1+|r|ρ+|s|ρ).

(3)

(4)

不失一般性，不妨設γ≥3.由條件(4)可推得，存在α<λ1滿足

φ1(r)r≥-αr2-c, ?r∈.

(5)

在以上假設條件下對方程(1)有如下結論.

定理1[4]對于任意ω>0,半群S(t)擁有一個連通的整體吸引子A=A(ω)?H0.

另外，還可以得到如下漸近衰減性結論.

推論1[4]當φ1≡0,f≡0時，S(t)衰減到0.因而,集合{0}?H0是S(t)在H0上的整體吸引子.

在本文，進一步對非線性項施加如下條件.

φ0(r)=0, ?r∈,

(6)

φ1∈C1(?r∈.

(7)

并且，對外力項假設

(8)

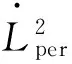
在以上基礎上將得到如下關于漸近正則性的結論.

定理2假設以上關于f和φ的條件(3)～條件(8)全部都成立.那么，存在M≥0,v>0以及H1中的一個有界閉集B1，滿足

distH0(S(t)B0,B1)≤Me-v t, ?t∈+.

其中,distH0表示在H0上的通常Hausdorff半度量.

在本文各種符號和函數空間的定義都與文獻[4]保持一致.

為了證明定理2，對于以初始值為z0=(u0,u1)∈H0的方程(1)的解u分解成2個部分u(t)=v(t)+w(t).其中，v和w分別滿足如下2個偏微分方程:

(9)

和

(10)

為了方便，引入如下符號

z(t)=(u(t),ut(t)),

zv(t)=(v(t),vt(t)),

zw=(w(t),wt(t)).

引理1[3]設Φ是一個在+上絕對連續的正函數,對ε>0,幾乎所有t∈+,滿足如下微分不等式

其中,g,h是在+上的函數，對某m1≥0和μ∈[0,1)，滿足

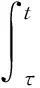
對某一m2≥0，有

那么，對于β=β(m1,μ)≥1和

(11)

有

Φ(t)≤βΦ(0)e-ε t+ρ, ?t∈+.

引理2給定σ∈[0,1],對Rσ≥0,假設‖z0‖≤Rσ.那么存在常數

Kσ=Kσ(Rσ)≥0,
Λσ=Λσ(Rσ)≥0,
μσ=μσ(Rσ)∈[0,1),

使得

‖z(t)‖σ≤Kσ, ?t∈+.

(12)

并且

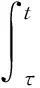
(13)

證對于σ=0的情況，由于方程(9)滿足推論1的條件，因而根據推論1，直接得到本引理結論.下面將證明，對給定σ∈[0,1),只要s滿足

那么，結論對σ+s同樣成立.從而，經過有限步的重復上述過程，對于任意σ∈[0,1]引理結論都成立.下面假設，對給定σ∈[0,1),條件(12)、條件(13)都成立.以下證明過程中常數c≥0可能與Rσ有關.證明分2種情況進行討論.

Φ(t)=‖A(1+σ+s)/2u(t)‖2-εω‖A(θ+σ+s)/2u(t)‖2+
‖A(σ+s)/2ξ(t)‖2+g(t)+k0,

(14)

其中，g的定義如下：

g(t)=2〈φ1(u(t)),Aσ+su(t)〉-2〈f,Aσ+su(t)〉.

計算

2|〈φ1(u),Aσ+su〉|≤

c(1+‖Aq/2u‖)‖A(1+σ+s)/2u‖,

其中，q=max{4σ+2s+γ-2γσ-3/2,0}.

由于q<1+σ+s,利用式(12)可得，對足夠小的常數v>0,存在cv=cv(Rσ)>0,使得

‖Aq/2u‖≤v‖A(1+σ+s)/2u‖+cv.

這將得到如下不等式

對2|〈f,Aσ+su〉|可直接得到如下不等式

在φ(t)的定義中，可以選取足夠大的k0和足夠小的ε0,使得對所有ε∈[0,2ε0]都有不等式

(15)

成立.另一方面,由Φ(t)的定義以及附加條件(8),可得

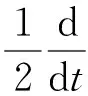
(16)

其中，

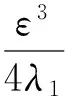
(17)

從條件(4)和式(15)可得

(18)

利用不等式(17)和不等式(18),從式(16)可得

(19)

其中，h(t)=c‖A(θ+σ)/2ut(t)‖.利用式(14),式(16),式(19),可得

因而，當選取ε0足夠小的時候，對所有ε∈[0,2ε0],都有

(20)

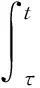
(21)

考慮到

由此，式(20)和式(21)中，Φ,h和μ滿足引理1的條件.從而，根據引理1,當ε=ε0時，利用式(15)得到

根據式(11)，其中的ρ的值為

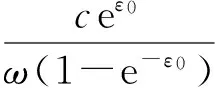
在區間(τ,t)上，對t進行積分，再利用式(21)，得到，對σ+s式(13)同樣成立.

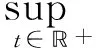
基于這個估計式，類似于情況1的證明，可以得到引理2的最終結論.

引理3給定σ∈[0,1),并設

(22)

對任意給定Rσ≥0,存在Rσ+s=Rσ+s(Rσ),當‖z0‖σ≤Rσ時，有

‖zw(t)‖σ+s≤Rσ+s, ?t∈+.

證在此引理證明中規定常數c≥0是依賴于Rσ的值.定義能量函數

Φw(t)=‖A(1+σ+s)/2w(t)‖2-εω‖A(θ+σ+s)/2w(t)‖2+‖A(σ+s)/2ξw(t)‖2+gw(t)+k0.

其中,ε>0,k0=k0(Rσ),ξw=wt+εw,并且

gw(t)=2〈φ1(u(t)),Aσ+sw(t)〉-2〈f,Aσ+sw(t)〉.

由于

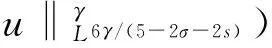
因而，當取k0的值足夠大，ε的值足夠小的時候，可使

利用連續嵌入公式，可得

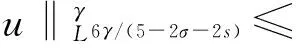
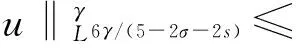
綜合以上2種情況，得到不等式

另一方面，考慮到Young不等式

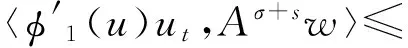
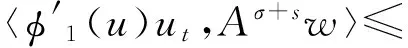
現在，對式(10)兩端與Aσ+sξw做內積，當取ε>0足夠小的時候，由于h滿足式(21)，從而

最后，利用引理1即可得到本引理的結論.

引理4[6]設K1,K2,K3是H0的子集，對?1，?2≥0和L1，L2≥0,如果

distH0(S(t)K1,K2)≤L1e-?1t,

distH0(S(t)K2,K3)≤L2e-?2t,

并假設，對任意z1，z2∈∪t≥0S(t)Kj(j=1,2,3)，有

‖S(t)z1-S(t)z2‖0≤L0e?0t‖z1-z2‖0.

其中，?0≥0,L0≥0.那么

distH0(S(t)K1,K3)≤Le-?t.

distH0(S(t)Bσj-1，Bσj)≤Mje-v0t， ?j=1,…,n．

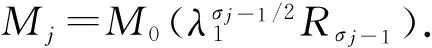
distH0(S(t)B0,B1)≤Me-v t．

這就證明了定理結論．

從B1出發的解滿足額外的正則性．

推論2存在常數c≥0，對t≥1，使得supz0∈B1‖zt(t)‖0≤c.

證對初始條件z0=(u0,u1)∈B1，考慮非齊次線性方程

(23)

此方程是對方程(1)關于t求微分所得的．在引理2中，當σ=1時，得到

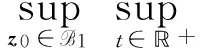
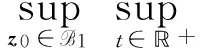
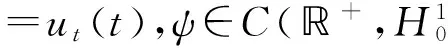
對于給定的r∈[t,t+1],把上面不等式在區間(r,t+1)上做積分，然后利用Gronwall引理得到本推論的結論.

[1] CARVALHO A N,CHOLEWA J W.Local well posedness for strongly damped wave equations with critical nonlinearities[J]．Bull Austral Math Soc,2002，66(3)：443-463．

[2] HALE J K.Asymptotic behavior of dissipative systems[M].Providence,RI:Amer Math Soc Providence,1988:134-159.

[3] ARRIETA J,CARVALHO A N，HALE J K．A damped hyperbolic equation with critical exponent[J].Comm Partial Differ Eqs,1992,17(5/6):841-866.

[4] 韓英豪，劉拓，杜萍，等．具有周期邊界條件的強阻尼波動方程的整體吸引子[J].遼寧師范大學學報(自然科學版)，2016,39(4):443-450.

[5] BELLERI V，PATA V．Attractors for semilinear strongly damped wave equation onR3[J]．Discrete Contin Dynam Systems，2001，7(4)：719-735．

[6] CARVALHO A N,CHOLEWA J W．Attractors for strongly damped wave equations with critical nonlinearities[J].Pacific J Math,2002,207(2):287-310.

[7] TEMAM R．Infinite-dimensional dynamical systems in mechanics and physics[M]．New York：Springer,1997:179-334．

Regularityoftheattractorforsemilinearwaveequationswithfractionaldamping

HANYinghao,TIANYujia,LIUShuang,YANGYutong

(School of Mathematics, Liaoning Normal University, Dalian 116029, China)

In this paper, we investigate the asymptotic regularity of the solutions for the semilinear wave equations with fractional damping. Yinghao Han et al. have proved that for the problem with the critical nonlinearity, the associated semigroup possesses a universal attractor A on the phase-space H0. With the additional assumptions for the external thermfand nonlinearityφ, it is also possible to prove that the semigroup possesses a universal attractor A1on the phase-space H1. Clearly, A1?A. If we could prove that A is a bounded subset of H1, then on account of the maximality properties of universal attractors, we would have the reverse inclusion. In general, one cannot have an H1-bound for A assuming only the external thermf∈H-1(Ω). In this paper, we prove the boundedness of A in the space H1under certain assumptions forfandφ.

asymptotic regularity;fractional damping;semilinear wave equation

O175．29;O211．63

A

2017-07-06

國家自然科學基金資助項目(61304056)

韓英豪(1963- )，男(朝鮮族)，遼寧師范大學副教授，博士.

1000-1735(2017)04-0433-07

10.11679/lsxblk2017040433