基于連續函數為自變量的Bernstein多項式的推廣及其曲線曲面應用
孫曉坤, 張 妍
(1.大連理工大學 城市學院 基礎教學部,遼寧 大連 116600; 2.遼寧師范大學 數學學院,遼寧 大連 116029)
基于連續函數為自變量的Bernstein多項式的推廣及其曲線曲面應用
孫曉坤1, 張 妍2
(1.大連理工大學 城市學院 基礎教學部,遼寧 大連 116600; 2.遼寧師范大學 數學學院,遼寧 大連 116029)
用一般的連續函數h(x)替換經典Bernstein基的參變量x,對經典Bernstein多項式進行了推廣.通過實例說明,這樣得到的Bernstein多項式雖然不一定具有原Bernstein多項式的收斂性,但給出了推廣的Bernstein多項式具有收斂性的條件.特別地,當h(x)是折線函數時,推廣的Bernstein多項式也可能不具有可導性、保凸性、凸包等性質.而這種推廣的Bernstein多項式的優勢在于,可以通過調整折線函數的參數值,產生不同于經典形狀的曲線和曲面,對自由曲線、曲面的設計具有一定的價值.
Bernstein多項式;折線函數;可導性;保凸性;凸包性質;自由曲線和曲面
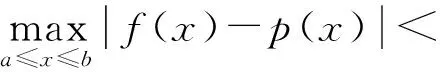
為證明Weierstrass定理,數學家Bernstein構造了一種特殊的多項式[2]:

(1)
式(1)稱為f(x)的n次Bernstein多項式,其中,f(x)在閉區間[0,1]上有定義,

(2)
稱為Bernstein基函數.
在Weierstrass定理基礎上,Bernstein利用式(1)構造性地證明了定理1.

函數的Bernstein多項式簡便、精練,容易構造,且當f(x)具有界性、單調不減、凸性等性質時,Bn(f;x)同樣具有上述性質,并且還具有可導性、凸包性質等特點[3-4].這使得Bernstein多項式的推廣和應用問題成為數值逼近理論的重要研究方面,為自由曲線、曲面設計提供了重要的數學工具[5].
在研究過程中,人們發現如果舍棄了經典Bernstein多項式的諸如可導性、凸性等優越性質,可以得到更廣泛的推廣和應用.本文就是對Bernstein多項式進行這樣一種推廣及應用:首先,以[0,1]上的一類連續函數h(x)取代經典Bernstein基函數和多項式中的x,得到推廣的Bernstein基函數與多項式,并討論其性質;其次,討論h(x)是折線函數時,推廣的Bernstein多項式的可導性、凸包、凸性等性質;最后,應用這種推廣的Bernstein多項式去生成自由曲線與曲面的形狀.
1 推廣的Bernstein多項式的性質
考察式(2)中的Bernstein基函數,其中,參變量x可視為函數h(x)≡x.那么,當h(x)≠x時,f(x)的Bernstein多項式Bn(f;h;x)是否仍收斂于f(x)?其次,Bn(f;h;x)的性質與h(x)有什么關系?再次,這類Bernstein多項式有何應用?
在此,要求[0,1]上的函數h(x)滿足h(0)=0,h(1)=1.
1.1 推廣的Bernstein多項式的收斂性問題
以h(x)替代式(2)中的x得到推廣的基函數,記為

(3)
這種基函數相當于對Bv,n(x)作代換x=h(t)(t∈[0,1])得到(仍記參變量為x),因此,Bv,n(h;x)自然保有Bv,n(x)大部分的優越性,如非負性、規范性、對稱性等[4].
同理,對式(1)作代換x=h(t)(t∈[0,1]),定義


現拋棄這種變換方法,直接定義Bn(f;h;x)為

(4)
其中,h(x)是[0,1]上的連續函數.
這里以f1(x)=x和f2(x)=x2為例,討論對應的Bn(f;h;x)的收斂性.
由于




因此

可見當h(x)≠x時,對于任意的f(x)∈C[0,1],{Bn(f;h;x)}不一定收斂于f(x).并且有如下一般性結論:
命題1設f(x)∈C[0,1],Bn(f;h;x)如式(4)所定義,則Bn(f;h;x)收斂于f(x)的充分必要條件是h(x)≡x.
命題2如果f(x)∈C[0,1]是以1,h(x),h2(x),…為基底的函數,則Bn(f;h;x)收斂于f(x).
1.2 h(x)為折線函數時Bernstein多項式的性質
多項式Bn(f;h;x)保有Bn(f;x)的部分性質,如有界性:若f(x)有界,則Bn(f;h;x)有界;單調性:若f(x)和h(x)在[0,1]上單調,則Bn(f;h;x)也單調;但當h(x)表示不同類型的函數時,Bn(f;h;x)的可導性、凸包性質、凸性等性質需單獨討論.下面重點研究h(x)為[0,1]上折線函數時的情形.

(5)

對式(5)求一階導數,得




圖1 Bn(f;h;x)不具凸包性質Fig.1 Bn(f;h;x) without convex hull property

圖2 Bn(f;h;x)不具凸性Fig.2 Bn(f;h;x) without convexity
因此,如果h(x)為折線函數,Bn(f;h;x)可能會失去經典Bernstein多項式的諸如可導性、凸包性、凸性等性質,但同時可以創造出更多的自由曲線和曲面的形狀,為Bernstein多項式帶來更多的應用.
2 h(x)為折線函數時,Bernstein多項式的曲線曲面應用問題
這里選定f(x)=-x2+x+1,x∈[0,1](見圖3).此時,經典Bernstein多項式B3(f;x)和B3(f;h;x)分別為

圖3 生成函數f(x)=-x2+x+1Fig.3 Generate function f(x)=-x2+x+1

2.1 參數t在(0,)內取值的情形

其圖形和經典Bernstein基的參變量x(y=h(x)=x)的圖形見圖4.

圖4 折線函數和y=xFig.4 Polygonal function (x) and y=x

∑1=B3(f;h;x)×B3(f;h;y),
∑2=B3(f;x)×B3(f;y),

圖5 t1=時的B3(f;h;x)和B3(f;x)Fig.5 Figures of B3(f;h;x) and B3(f;x) as t1=
曲面Σ1表現出4個小曲面的銜接過渡,比曲面Σ2的形狀要復雜得多.

圖6 t1=時的曲面Σ1和Σ2的對比Fig.6 Contrast of surface Σ1 and surface Σ2 as t1=

圖7 t1=和t2=時的B3(f;h;x)Fig.7 Figures of B3(f;h;x) as t1= and t2=

2.2 參數t在(,1)內取值的情形

討論方式同t1,生成的曲線B3(f;h;x)見圖9,對應的曲面見圖10.圖9顯示t3時曲線改變的方向與t1時相反,這一結果直接影響了曲面Σ1=B3(f;h;x)×B3(f;h;y)的狀態.
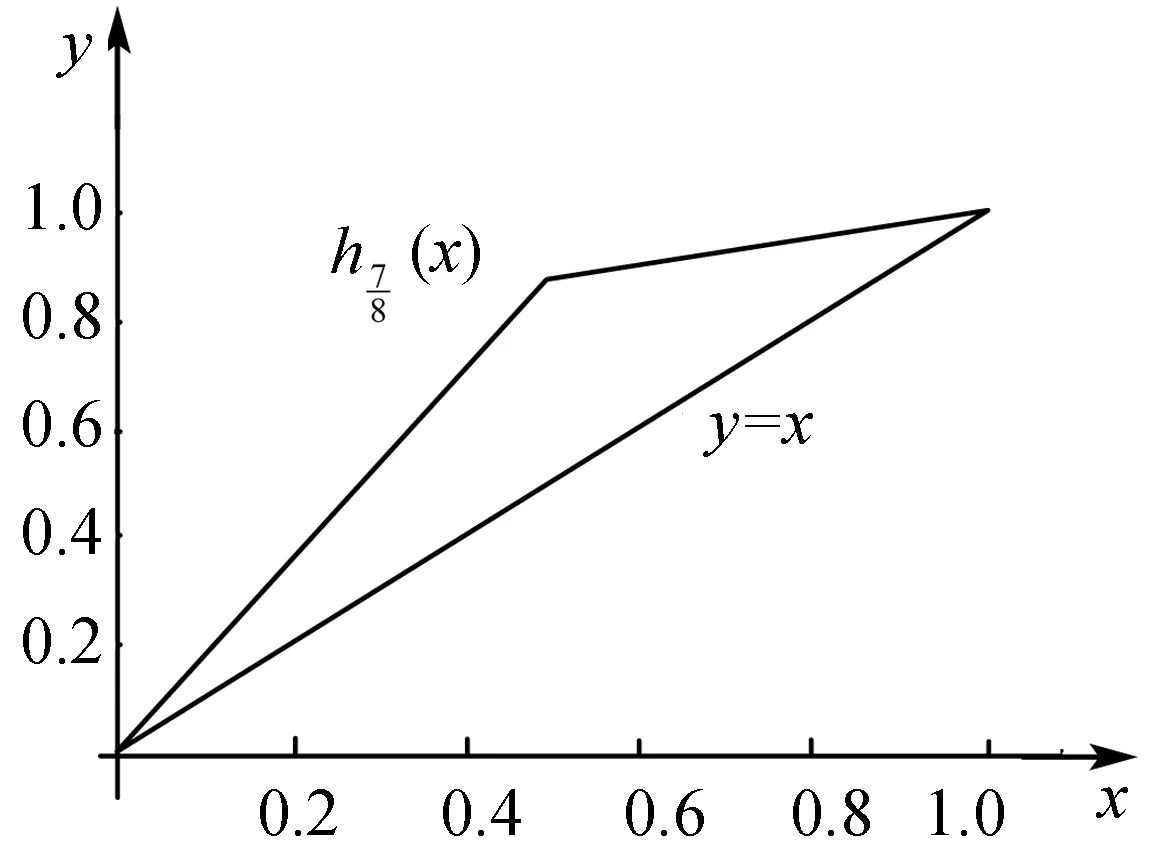
圖8 折線函數和y=xFig.8 Polygonal function (x) and y=x

圖9 t3=時的B3(f;h;x)和B3(f;x)Fig.9 Figures of B3(f;h;x) and B3(f;x) as t3=

圖10 t3=時的曲面Σ1和Σ2Fig.10 Surface Σ1 and Σ2 as t3=

圖11 t3=和t4=時的B3(f;h;x)Fig.11 Figures of B3(f;h;x) as t3= and t4=


致謝 本文的撰寫得到了遼寧師范大學數學學院王晶昕教授的悉心指導.王教授嚴謹的治學精神和對研究的精辟見解,使作者受益良多,對作者今后的工作、學習和研究都將產生巨大的影響,在此表示衷心的感謝!
[1] 王仁宏.數值逼近[M].北京:高等教育出版社,1999:1-5.
[2] BERNSTEIN S.Démonstration du théorème de Weierstrass fondée sur le calculdes probabilities[J].Comm Soc Math Khardov,1912,13:1-2.
[3] LORENTZ G G.Bernstein polynomials[M].Toronto:Math Expo Univ of Toronto Press,1953:5-29.
[4] 施法中.計算機輔助幾何設計與非均勻有理B樣條[M].北京:北京航空航天大學出版社,1994:124.
[5] 王晶昕,王圓圓.Bézier曲線的單側降階通近[J].遼寧師范大學學報(自然科學版),2009,32(1):1-3.
GeneralizationofBernsteinpolynomialswithindependentvariableiscontinuousfunctionandapplicationsoffreecurvesandsurfaces
SUNXiaokun1,ZHANGYan2
(1.City Institute, Dalian University of Technology, Dalian 116600, China;2.School of Mathematics, Liaoning Normal University, Dalian 116029, China)
This paper generalizes Bernstein polynomials replacexin classical Bernstein Bases with continuous functionh(x),however this generalized Bernstein polynomials doesn’t always converge to generating functionf.Especially,ifh(x) is a polygonal function,generalized Bernstein polynomials do not always have differentiability,convexity preserving property and convex hull property,etc.And then,we study curves and surfaces of this generalized Bernstein polynomials by adjusting parameter ofh(x),etc.
Bernstein polynomials;polygonal function;differentiability;convexity preserving property;convex hull property;free curves and surfaces
O241.5
A
2017-07-20
孫曉坤(1978- ),女,遼寧大連人,大連理工大學副教授.
1000-1735(2017)04-0456-06
10.11679/lsxblk2017040456

