基于有限元方法的變壓器鐵芯優化仿真*

劉旭光，顧小虎，于春雷，張曉同，劉斌，楊慶福

（1.南瑞集團公司＜國網電力科學研究院＞，南京 211100；2.江蘇南瑞帕威爾電氣有限公司，南京 211100；3.南昌航空大學，南昌 330000）

0 引 言

隨著城市與農村電網建設的快速發展，變壓器的需求量呈快速增長的趨勢，它是否節能十分重要［1］。變壓器自身的能量消耗有兩種：一種是鐵芯產生的空載損耗，另一種是主要由導線產生的負載損耗［2］。雖然空載損耗比額定負載損耗小很多，但只要產品掛網運行，不管負載大小，空載損耗總是存在的，尤其在變壓器輕載情況下，空載損耗占總損耗的比重很大。因此，降低空載損耗是變壓器技術發展的一個趨勢。

變壓器鐵芯柱截面的大小直接關乎銅材的使用量，在保持其他參數不變的情況下，心柱截面積增大，磁通密度降低，損耗減少，但其截面積增大，銅材的使用量增多。若以增大原材料的使用量為代價來減少空載損耗則得不償失。文獻［3］和文獻［4］對降低空載損耗的方法進行了簡要的闡述，通常都是從硅鋼材料的升級、工藝的改進等方面進行分析，并未提出鐵芯結構上的改進方法。針對上述問題，采取一些可行方法達到降低空載損耗的目的，本文提出增大鐵軛截面積以降低空載損耗的方法，并通過四維可視化算法進行理論分析和有限元分析軟件仿真驗證，在保證成本可控的情況下，達到降低損耗目的。

1 空載損耗理論分析研究

空載損耗主要包括磁滯損耗、渦流損耗。通常空載損耗數值為變壓器鐵芯重量、鐵芯材料的單位損耗、鐵芯加工工藝系數三者的乘積，而其鐵芯材料的單位損耗由磁通密度的大小確定，可見空載損耗與鐵芯重量、磁通密度有關。

變壓器鐵芯損耗的計算已經提出一些有效模擬方法，諸如均勻化處理等方法，但是鐵芯在垂直進入的漏磁通作用下所產生的損耗與通常損耗不同，稱之為附加損耗。對于大型變壓器多級鐵芯的“末級鐵”內部由于變壓器線圈漏磁通進入，將產生可觀的渦流損耗［5］。當外施交變磁場垂直進入取向硅鋼疊片組時，面臨磁通進入的若干張硅鋼片中可能感應出很強渦流，由此產生的渦流損耗在總鐵損中可能占據一定比重。實際中硅鋼片中除了垂直進入的漏磁通外，還通過與硅鋼片平行的交變磁通，產生的渦流為三維，其僅限于單片內部流動。在正弦磁通情況時，頻率范圍內空載損耗表達式為：

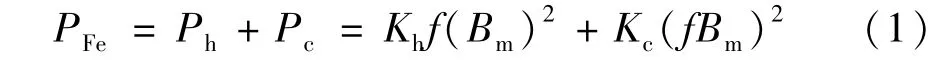
式中的Ph、Pc為磁滯損耗、渦流損耗；Kh、Kc為磁滯鐵芯單位損耗、渦流鐵芯單位損耗；f為工作頻率；Bm為交流磁通分量幅值。

有限元分析軟件常采用上式表達式進行空載損耗計算，其中Kh、Kc均由鐵芯材料制造廠商提供的損耗曲線得出。

2 變壓器數學模型及優化分析

鐵芯直徑的大小直接影響有效材料的消耗、變壓器體積及性能參數等技術經濟指標，因此選擇技術經濟合理的鐵芯是變壓器計算的重要內容［6］，合理的鐵芯直徑使得硅鋼片和導線用量的比例適當，達到最經濟效果。

根據電磁感應原理，繞組中的感應電勢為：

式中f、N、B、S分別表示為電網頻率、繞組匝數、磁通密度、鐵芯截面積。我國電網頻率為50 Hz，故感應電動勢數值與三個變量N、B、S表達，利用MATLAB軟件編程可得其可視化變化趨勢圖，如圖1所示。

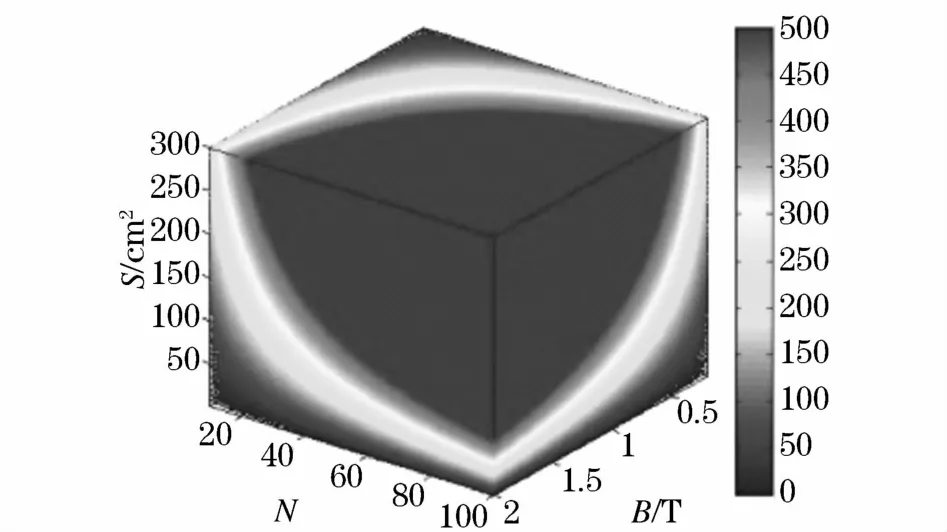
圖1 感應電動勢可視化圖Fig.1 Visualization diagram of induced electromotive force

圖1中三個變量N、B、S的取值范圍依次為（10，100）、（0.2，2）T、（1，300）cm2，由上圖可知三個變量的變化對感應電動勢呈非線性變化趨勢。圖1感應電動勢變化范圍為（0，500）V，淺色代表數值較小，深色代表數值較大；當變量增大時其可視化圖顏色加深，即感應電動勢增大。

本文設計的模型低壓側電壓為0.4 kV，故從圖1中求取滿足U=0.4 kV條件的解域，如圖2所示，圖中綠色區域（深色）即為函數U的解域集。

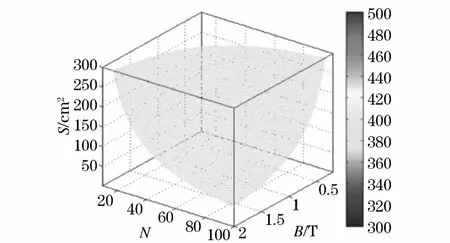
圖2 U=0.4 kV解集可視化圖Fig.2 Visualization diagram when U=0.4 kV solution set

由圖2可知，當感應電動勢一定時，B選取大，N不變時，則S較小，硅鋼用量較少；B選取小，N不變時，則S較大，硅鋼用量較大。

當變壓器空載損耗超出標準范圍較小時，傳統采用同時改變鐵芯芯柱、軛截面積方式降低空載損耗，易造成變壓器線圈材料增加。

以某公司S13-M-400變壓器產品為例，產品鐵軛截面積未加大前，其變壓器鐵芯損耗理論值為419 W，該數值超過設計標準值，未符合標準，故需找到一種合適方法解決該問題。通過幾組數據進行曲線擬合可知，當增大鐵軛截面積，鐵芯柱截面積不變，空載損耗隨鐵芯總重變化的趨勢如圖3所示。

圖3 空載損耗隨鐵芯重量變化圖Fig.3 Diagram of no-load loss change with the weight of the iron core

圖3中坐標點為空載損耗臨界點，即GB 1094中規定額定空載損耗410 W時，鐵芯總重對應為493.1 kg。當鐵軛截面積增大，相應的磁通密度降低，盡管鐵芯總重增大，但空載損耗下降明顯。空載損耗與磁通密度影響緊密，如若同時降低芯柱磁通密度，線圈成本就會增加，由上圖可知當鐵軛截面積的增大，成本增加幅度較小。

可見，鐵軛截面積增加對空載損耗的降低作用明顯，且可有效控制高性能變壓器材料成本。

3 變壓器模型計算

變壓器空載損耗計算是變壓器設計中一個較困難問題，目前設計工程師常利用鐵芯平均磁通密度方法進行空載損耗計算，雖然其可滿足工程需求，但鐵芯磁通密度分布無法進行精確測量，對于產品的性能優化有一定局限性［7］，故需利用有限元方法進行計算驗證。

本文利用有限元分析軟件在瞬態場進行變壓器鐵軛加大前后模型的仿真計算。求解三維瞬態磁場時，其棱邊上的矢量位自由度采用了一階元計算，而節點上的標量位自由度采用二階元計算［8］。

電磁分析實際是求解給定邊界條件下的麥克斯韋爾方程組問題，是電磁場數值計算和應用研究的基礎［9］。三維瞬態場采用T-Ω算法，利用局部剖分法計算三維瞬態所帶來的效應，對于低頻瞬態磁場，麥克斯韋方程組表達式為：

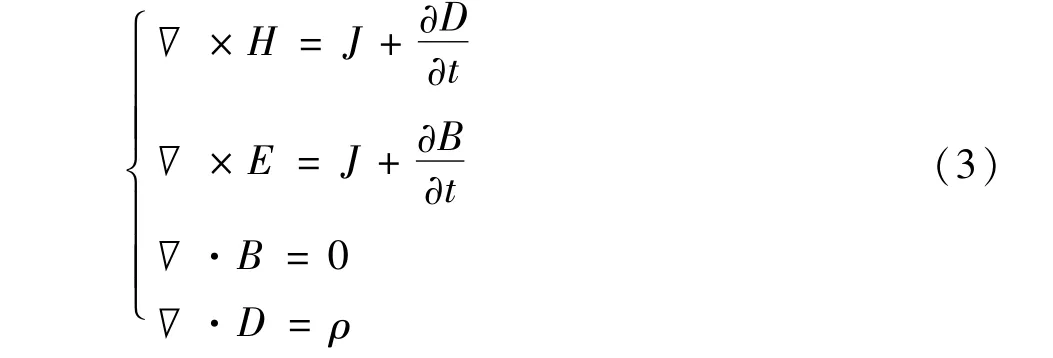
式中E、H、D、B、J、ρ分別為電場強度、磁場強度、電通量密度、磁通量密度、電流密度和電荷密度。對上式方程組中的第一個方程進行取散度，利用第四個方程結果可得：

式中ε、μ、σ分別表示媒質介電常數、磁導率和電導率。由于變壓器沒有自由電荷，電荷密度可忽略，即式（4）為0。

依據上述理論分析，針對鐵軛截面積增加進行優化設計，變壓器空載損耗優化設計前后基本參數如表1所示，模型材料屬性如表2所示。

表1 性能參數Tab.1 Performance parameters

表2 材料屬性Tab.2 Material properties

鐵軛截面積增加范圍由鐵芯牌號、鐵芯結構尺寸、制造工藝等因素決定［10-11］，本文模型鐵軛橫截面積增加約6.47%左右。變壓器鐵芯主級片寬為140 mm，仿真環境設置除鐵軛面積不同，其余參數均一致，本文針對優化前后兩種模型進行仿真驗證。

4 空載損耗優化仿真

對于結構簡單模型來說，常采用有限元分析軟件進行二維模型建模分析，但鑒于其變壓器鐵芯為疊片形式，結構相對復雜；為提高仿真計算精度，故應采取三維模型進行仿真分析。

由于筆者主要研究變壓器磁場分布及空載損耗分析，為節省仿真計算時間及提高效率，筆者將變壓器簡化模型進行1/2求解計算。由于本文僅研究鐵軛加大對空載損耗，故該變壓器模型其余結構件可忽略，其中激勵源采用電壓源，不考慮諧波影響。

利用有限元軟件在瞬態場進行分析計算，優化前后模型時刻鐵軛加大前后磁通密度變化及分布，其結果如圖4所示。

由圖4可知，鐵軛橫截面積未加大前，該變壓器鐵軛磁通密度顏色較深，即其鐵軛磁通密度較大；鐵軛橫截面積增加后其顏色較淺，即其鐵軛磁通密度較小。在變壓器模型中取鐵軛上某點進行仿真計算，查看該點磁通密度變化情況，如圖5所示。

圖4 t=0.086 2 s時刻鐵芯磁通密度分布Fig.4 Distribution of magnetic flux density when t=0.086 2 s

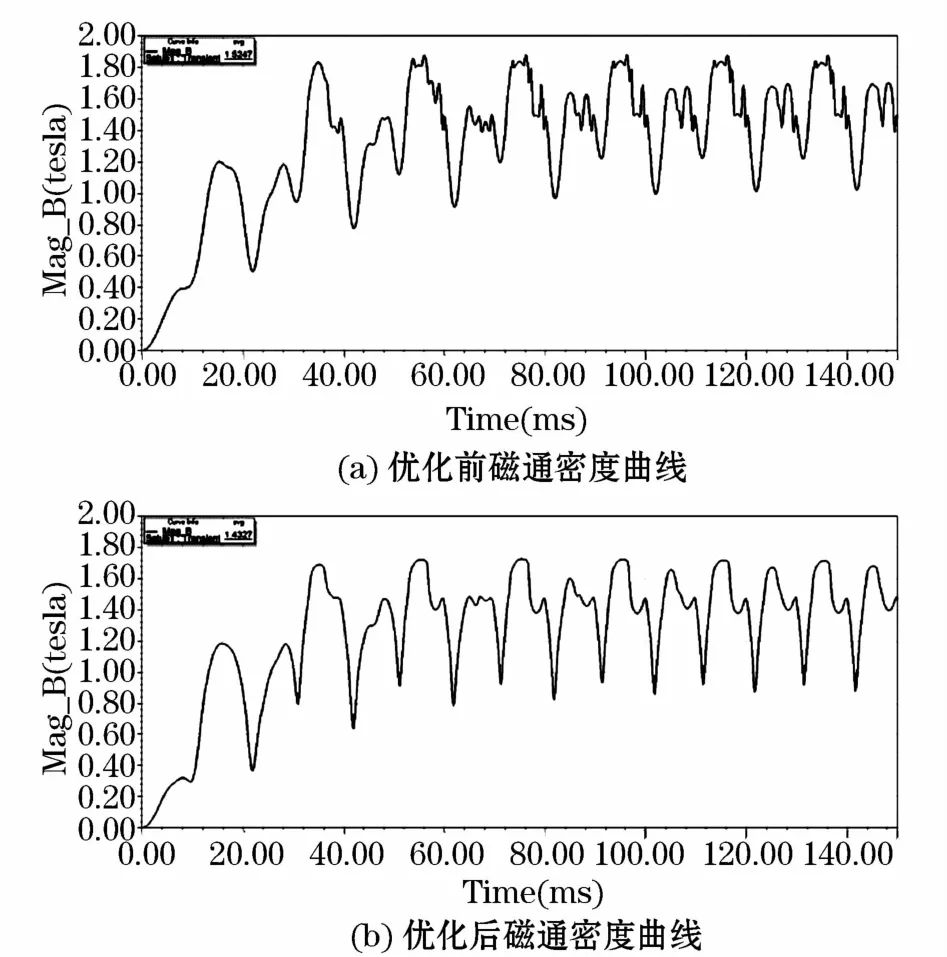
圖5 鐵芯磁通密度分布Fig.5 Distribution of magnetic flux density

圖5（a）為鐵軛優化前某點磁通密度變化，其鐵軛平均磁通密度為1.524 7 T，圖5（b）為鐵軛優化后某點磁通密度變化，其鐵軛平均磁通密度為1.432 7 T。依據磁通量不變原理，由于優化鐵軛橫截面積增大，激勵源不變，故其磁通密度降低，上述仿真磁通密度結果也驗證符合理論計算。變壓器模型優化前后空載損耗仿真計算，如圖6所示。

圖6 空載損耗曲線Fig.6 No-load loss curve

圖6為鐵軛優化前后空載損耗曲線，優化前其變壓器模型空載損耗仿真數值為417.144 7 W，質量為481.29 kg；改善后其數值為396.452 7 W，質量為494.45 kg；優化前后空載損耗數值下降約4.95%，質量增加2.78%，成本增加相比性能降低較優，驗證了設計可行性。

5 結束語

本文主要針對鐵軛截面積加大對變壓器磁場及損耗變化的影響進行了理論分析，利用有限元分析軟件仿真驗證其可行性。采用鐵軛加大方式可使得空載損耗降低，對于企業今后產品技術研究有推動作用。