近距離激光外差探測光學極限位移分辨率?

晏春回王挺峰張合勇呂韜吳世松2)

1)(中國科學院長春光學精密機械與物理研究所,激光與物質相互作用國家重點實驗室,長春 130033)

2)(中國科學院大學,北京 100049)

近距離激光外差探測光學極限位移分辨率?

晏春回1)2)王挺峰1)?張合勇1)呂韜1)2)吳世松1)2)

1)(中國科學院長春光學精密機械與物理研究所,激光與物質相互作用國家重點實驗室,長春 130033)

2)(中國科學院大學,北京 100049)

激光多普勒測振,激光應用,激光

1 引 言

激光外差探測技術具有高精度、非接觸以及抗干擾等優點,同時較直接探測具有更好的靈敏度和信噪比,因而廣泛用于微弱振動信號的檢測.國內外相關研究主要應用在微振動目標檢測和速度測量、轉動目標頻譜識別及振動目標探測成像等領域.Kingston[1]對相干探測技術做了詳細的論述.相干探測技術典型系統有麻省理工學院林肯實驗室研制的Firepond雷達系統[2]和美國空軍實驗室牽頭開發的HI-CLASS系統[3].

外差探測即本振光(也叫參考光)與信號光經過分光棱鏡在探測器表面進行混頻,對混頻后所得中頻信號進行分析、處理,進而實現微弱信號光的檢測.外差探測中由于光信號的頻率極高,目前所使用的光電探測器無法對光波頻率進行直接探測.外差探測系統中以外調制的方式(一般使用聲光調制器)將光頻移頻到幾十兆赫茲,利用光相干疊加原理,將兩個頻率不同的相干光疊加使得高頻光波信號轉換為中頻包絡信號,從而實現對多普勒頻移的測量,進而得到微振動目標物的振動特性(振幅、相位、頻率).

近距離激光外差探測系統光學極限位移分辨率不僅取決于探測器的性能,也受到系統中其他部分如激光器、光學器件性能以及信號光和本振光的匹配情況等的影響.但是,探測器、激光器、光學器件的影響是主要的、直接的,其他影響因素可以轉化為探測器的信噪比和噪聲[4].因此,一般情況下討論外差系統的位移分辨率時,只考慮前者就足以說明問題.當進行遠距離的外差探測實驗時,則需要另外考慮大氣湍流的影響.

國內外外差探測相關的研究已經進行了很多年[5?8],但一直沒有見到外差系統光學極限位移分辨率的理論分析.本文分析了激光線寬、相干時間、探測距離對外差探測的影響,修正了相關文獻中光電流譜線分布的理論公式[9],建立了基于激光波長、探測距離、激光線寬的外差光學極限位移分辨率的數學模型,并得到由激光線寬引起的相位噪聲的一維概率分布模型,進行了相關的數值仿真.當外差探測系統參數均為典型值時,外差探測光學極限位移分辨率sn=0.266 nm.與相關文獻中的實驗數據相符合[10],可以為后續研究和實際應用提供理論支持,同時為外差探測系統激光器的選型、探測距離的極限提供定量的理論參考.

2 理論分析

2.1 激光線寬與光電流譜線分布

外差探測中考慮一準單色光源,其電磁場擾動的復數形式為

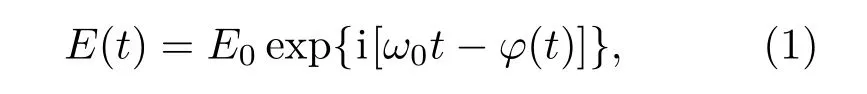
式中E0為電磁場振幅,ω0為電磁場平均頻率,φ(t)為電磁場相位隨機擾動.在近距離外差探測中,不考慮大氣湍流和目標調制所產生的隨機相位,回波光場和本振光場分別為:

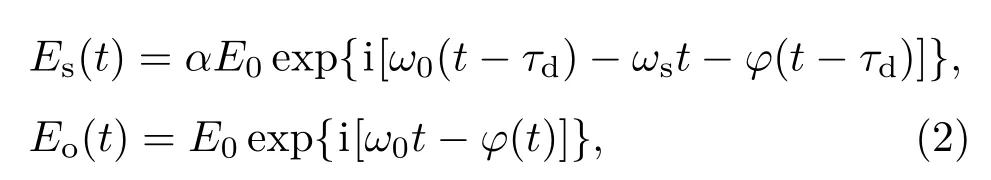
式中α為回波光與本振光的光場振幅之比;τd為信號光相對本振光的傳輸延遲時間;ωs為外差探測中信號光與本振光之間的頻率差,即外差探測最終所要獲取的中頻信號;φ(t?τd)為回波光經過延遲τd后的隨機相位抖動.只要ωs=2πfs小于光電探測器的截止響應頻率fc,那么探測器就有相應的光電流輸出.

根據光電探測器的平方律特性[11],其輸出光電流為

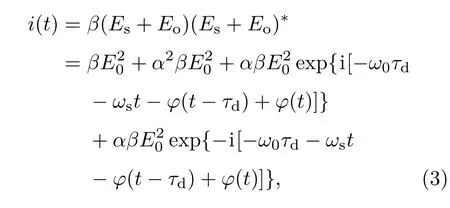
(3)式中參數β為探測器的光電轉換參數,此處假定探測器的量子效率是均勻的.為了后續分析的方便,取β=1,并將(3)式做些處理,記

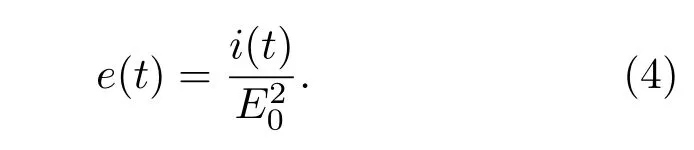
代入(3)式中的結果,得

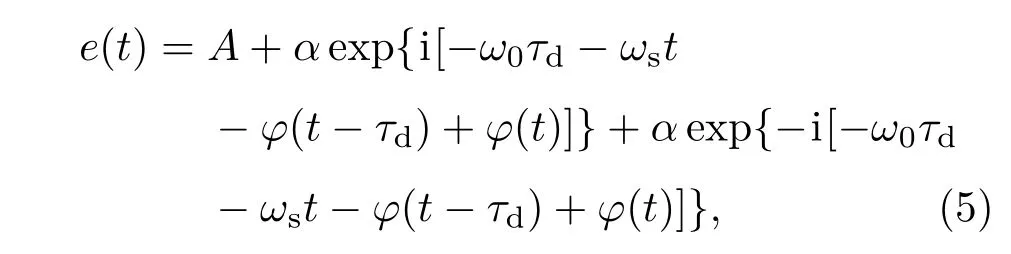
其中A=1+α2.

由維納-辛欽定理可知,自相關函數與對應的功率譜密度構成傅里葉變換對[12].因此可以通過光電流的自相關函數獲得光電流信號的功率譜,光電流的自相關函數G(τ)為

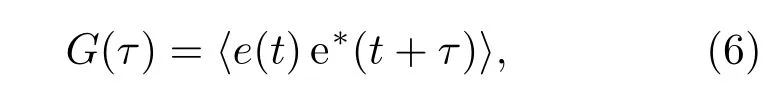
上式中〈···〉表示時間平均, 代入(5)式并做整理可得

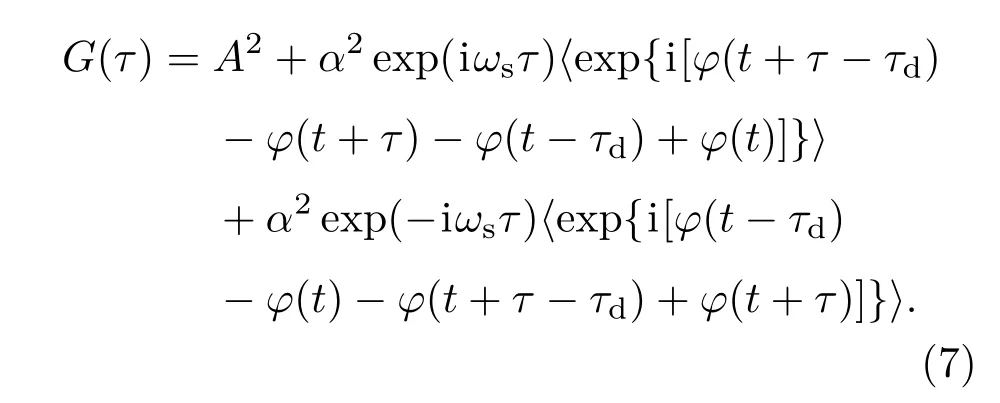
探測器的平方律特性使探測器輸出信號包含中頻信號和直流信號兩部分,并且中頻信號中存在隨機相位部分,隨機相位的存在會造成光電流頻譜的展寬.記

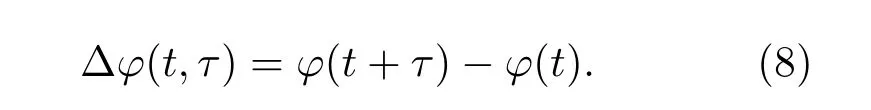
信號及噪聲理論認為,信號源的隨機相位跳動是一個平穩隨機過程,其服從零均值高斯分布,通過理論分析可得關系式[13]

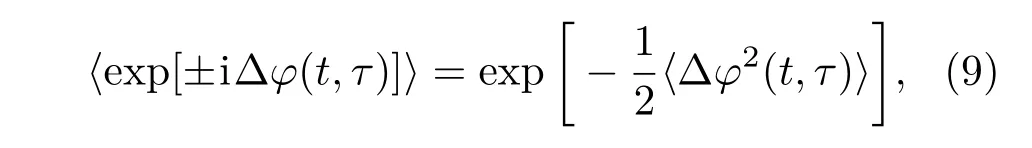
其中[14]

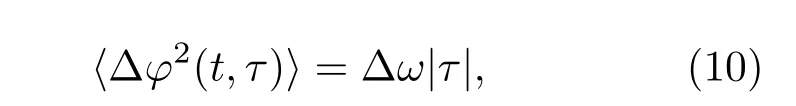
式中〈Δφ2(t,τ)〉是隨機相位方差的時間平均;Δω是Lorentzian型激光譜的半高全譜線寬,Δω=2πΔν對應的相干時間為τc=2π/Δω. 隨機信號的自相關函數具有偶函數的特性,所得結果要滿足這一特性,下面根據τ和τd的關系進行討論.

1)當τ≥τd

記

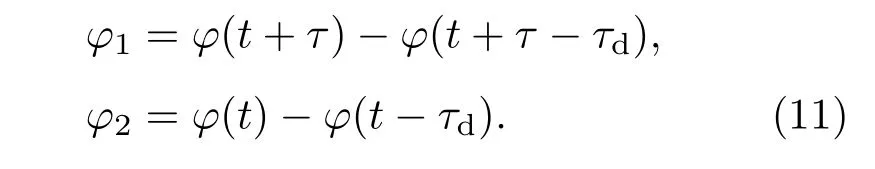
在τ≥τd的條件下,φ1和φ2相互獨立(因為沒有時間上的重疊),具體如圖1所示.

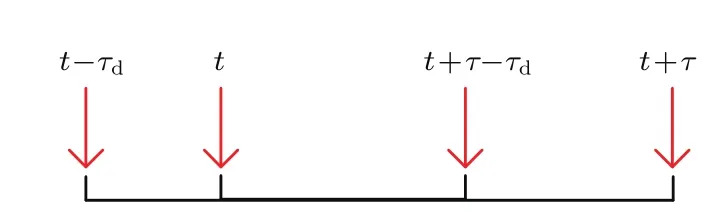
圖1 隨機相位的時間關系Fig.1.The timeline of random phases.

根據(9),(10)式中的結果及(11)式,對(8)式進行整理可得

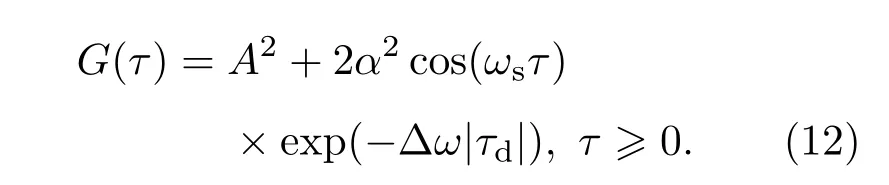
2)當τ＜τd

記

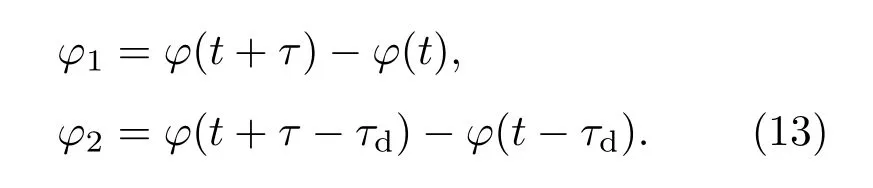
在τ＜τd的條件下,φ1和φ2沒有時間上的重疊,因此相互獨立,具體如圖2所示.

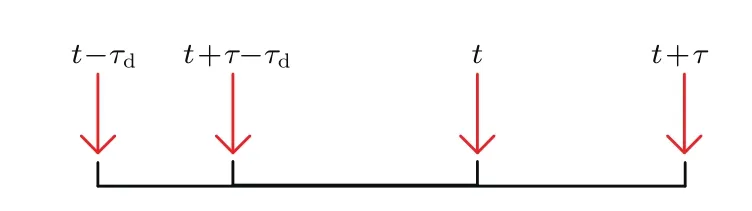
圖2 隨機相位的時間關系Fig.2.The timeline of random phases.

根據(9),(10)式中的結果及(13)式對(8)式進行整理可得

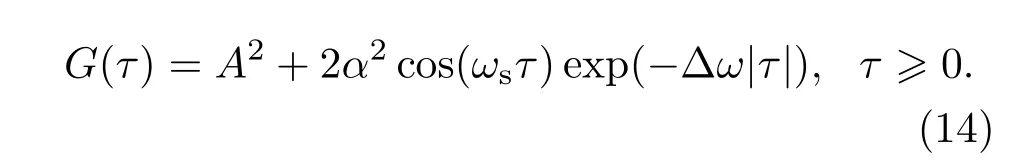
同理可推出當τ＜0時,

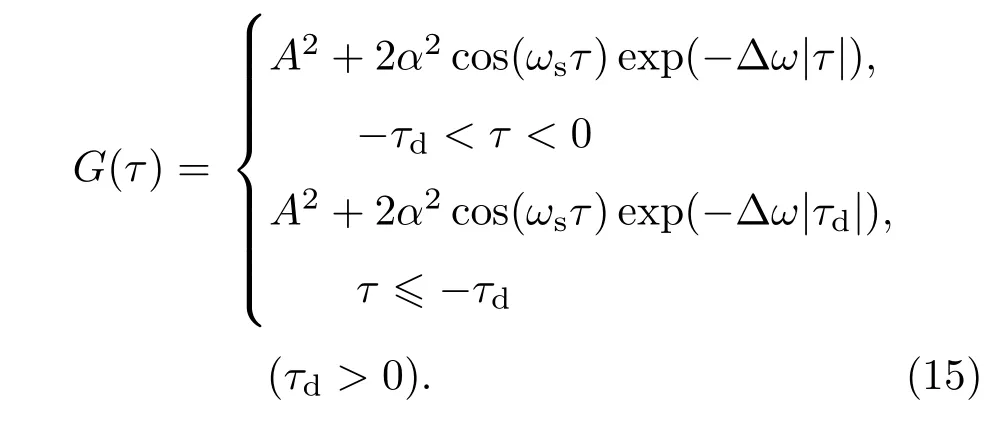
綜合可得光電流的自相關函數為

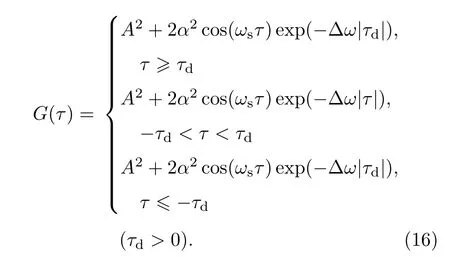
通過分析可以看出(16)式中的自相關函數為偶函數,現根據維納-辛欽定理[12],計算自相關函數G(τ)的功率譜,考慮到所得結果的真實物理意義,舍棄負頻率成分得

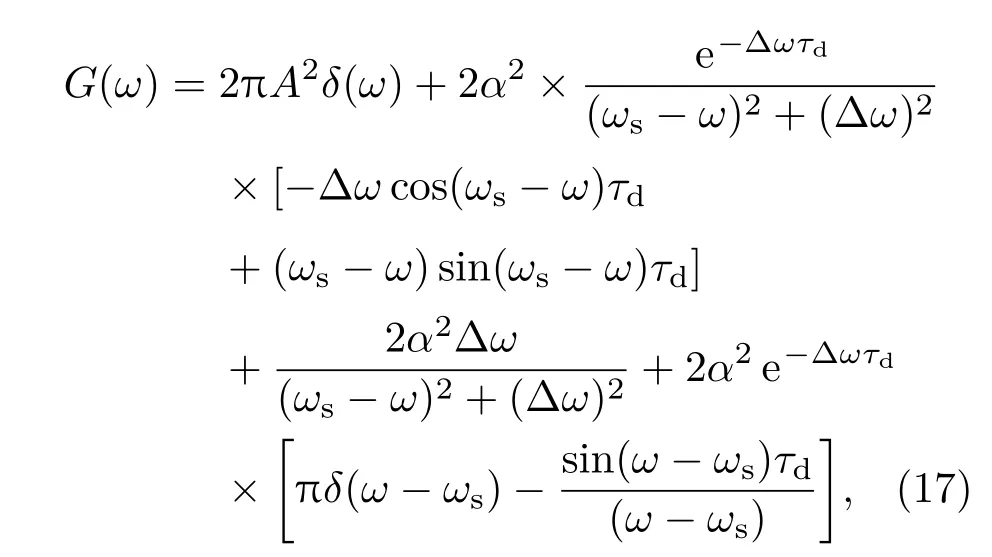
(17)式中含有激光光源線寬Δω、中頻頻率ωs、回波光相對本振光的傳輸延時τd=2d/c,d為外差探測距離.與相關文獻中的研究相比[9],(17)式光電流的功率譜函數多出一項,當延遲時間τd?τc或延遲時間τd與相干時間τc相近時,即進行近距離外差探測實驗時,光電流的譜線分布在整個頻域范圍內出現多個頻率峰值,中頻信號譜線分布接近高斯型,仿真中有具體說明;當延遲時間τd?τc時,即進行遠距離外差探測時,光電流的譜線分布呈現洛倫茲線型,且線寬越小越接近洛倫茲線型,與文獻中的結論一致.

2.2 外差系統光學極限位移分辨率

目前外差探測裝置中為了有效抑制本振光強度噪聲多用平衡探測器,平衡探測器輸出光電流為[15]

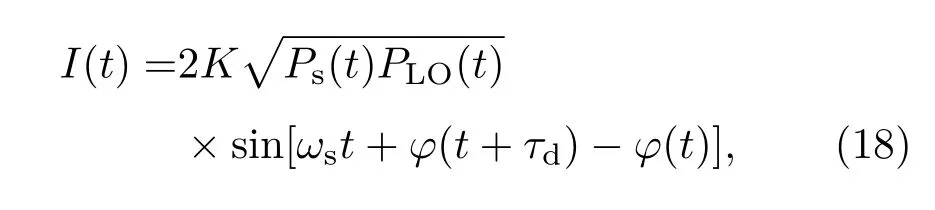
其中K為轉換參數K=ηq/(hν),η是量子效率,q是一個電子的電荷量),h為普朗克常量,υ為光的頻率,Ps是信號光功率,PLO是本振功率(參考光功率),ωs是中頻信號的角頻率,其中

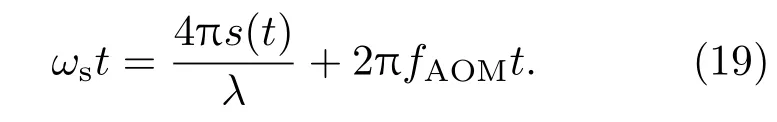
應用正交解調算法對I(t)分別與正弦載波和余弦載波相乘,并利用低通濾波器濾掉高頻噪聲,得到兩路正交信號:

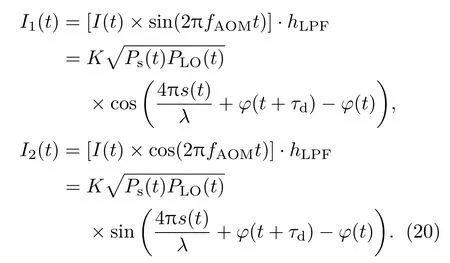
經過反正切算法即可得到含有相位噪聲的目標物振動信號:

s(t)為需要求得的解調輸出結果,激光頻率的抖動可以轉化為相位噪聲,相位噪聲Δφ(t)服從零均值高斯分布,即均值μ=0

考慮到激光器發射高斯型激光譜線,則相位噪聲的方差[16]

其中τd為信號光和本振光之間的延遲時間,τd=2d/c,d為探測距離,Δω為高斯型激光譜的半高全譜線寬,則相位噪聲的一維概率分布模型:

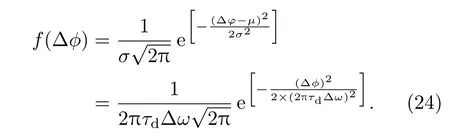
高斯分布服從“3σ準則”,即Δφ分布在(?σ,+σ)區間的概率為68.27%,分布在(?2σ,+2σ)區間的概率為95.45%,分布在(?3σ,+3σ)區間的概率為99.74%.可以認為Δφ的取值幾乎全部集中在(?3σ,+3σ)區間內,超出這個范圍的概率不超過0.3%.

可以認為輸出解調結果最差的情況如下:

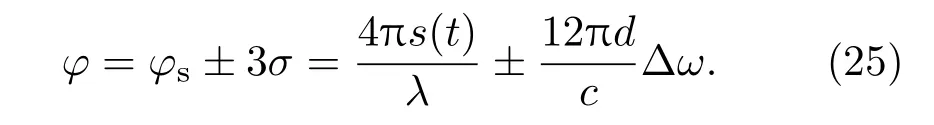
在近距離激光外差探測系統中,不考慮大氣湍流的影響,其光學極限位移分辨率與信噪比直接相關,探測器的信噪比如下[17]:

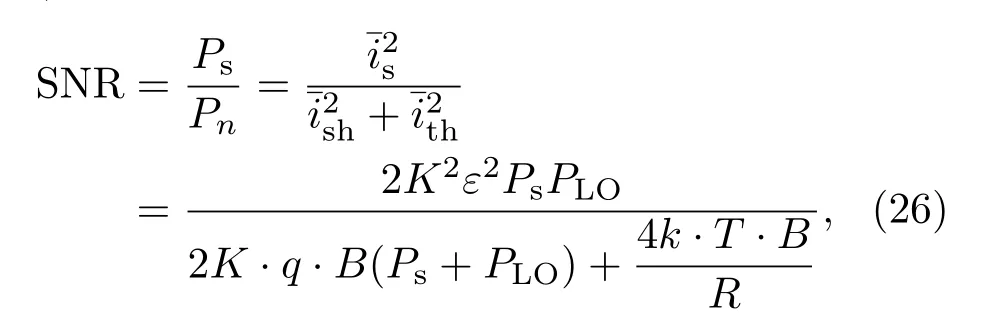
由于本振功率的存在,散粒噪聲遠大于熱噪聲

峰值為Un的噪聲信號所造成的最大相位偏差[17]:

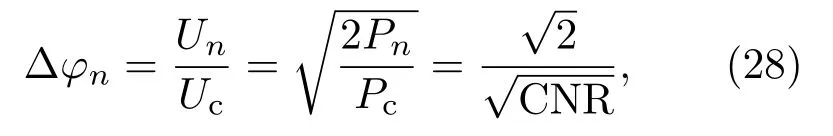
其中Uc為載波信號幅值,Pn為噪聲有效功率,Pc為載波信號功率,CNR為外差系統的載噪比.載噪比定義為探測器輸出信號的交流成分與散粒噪聲的比值

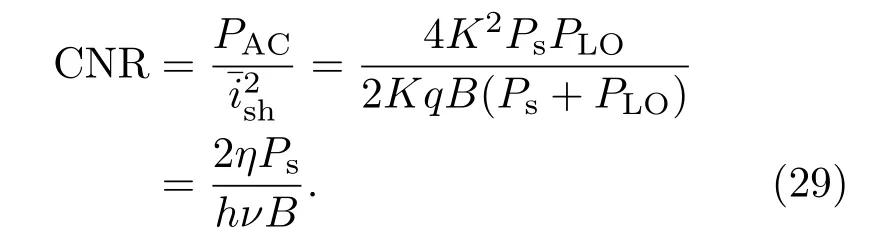
所以外差探測系統信噪比與載噪比之間的關系如下:

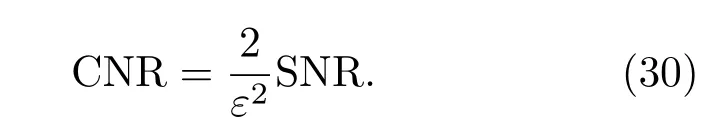
由(28)和(30)式可得

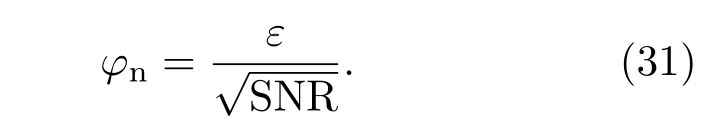
相位與目標物振動位移之間的關系Δφ=4πΔs/λ,將SNR=1[18]時可以解調出的目標物振動幅度認為是外差探測系統的極限位移分辨率,近距離外差探測系統的光學極限位移分辨率如下:

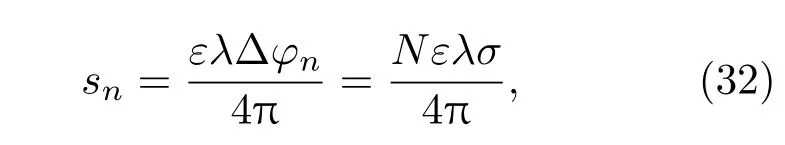
N取1時外差探測系統可以精確探測目標物振動的概率為68.27%,N取2時的概率為95.45%,N取3時的概率為99.74%.若想長期穩定地對目標物的微振動進行探測,則N取3,即

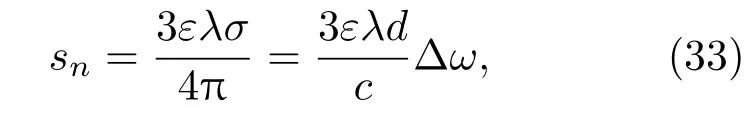
(33)式是本文理論分析的核心公式,據此討論近距離激光外差探測光學極限位移分辨率.由(33)式可知,外差探測光學極限位移分辨率與探測器光電轉換效率、激光波長、探測距離以及激光線寬成線性相關.探測器轉換效率越高、激光波長越長、探測距離越大、激光線寬越寬,外差系統可探測到的光學極限位移越大,光電流譜線分布的仿真結果也與理論分析相符合.

3 數值仿真

激光線寬、相干時間、探測距離對外差探測的影響可以根據(17)式討論,進行數值仿真時所用激光光源波長λ=532 nm.延遲時間與相干時間的大小關系決定了光電流譜線分布的情況.圖3中可以明顯看出探測器輸出信號的中頻頻率位置所對應的尖峰,即公式中所對應的帶有狄克拉函數成分的項.

1)延遲時間大于相干時間

仿真中設激光線寬分別為1,10,100 kHz,延遲時間τd=100τc(τc為相干時間). 信號光與本振光的振幅之比α=0.1,聲光調制器的頻率ωs=40 MHz,激光平均波長λ=532 nm.將上述數值代入(17)式中可得圖3所示不同激光線寬的光電流譜線分布,中心頻率為40 MHz的中頻信號由于相位噪聲的影響而變寬,且線寬越小,光電流譜線的半高全寬(FWHM)越小,中頻信號的檢測越容易.從(33)式中也能看出,激光線寬越小,外差探測系統可探測的最小位移越小.考慮到系統受環境噪聲及系統本身噪聲影響,線寬達到一定寬度,中頻信號可能檢測不準確.

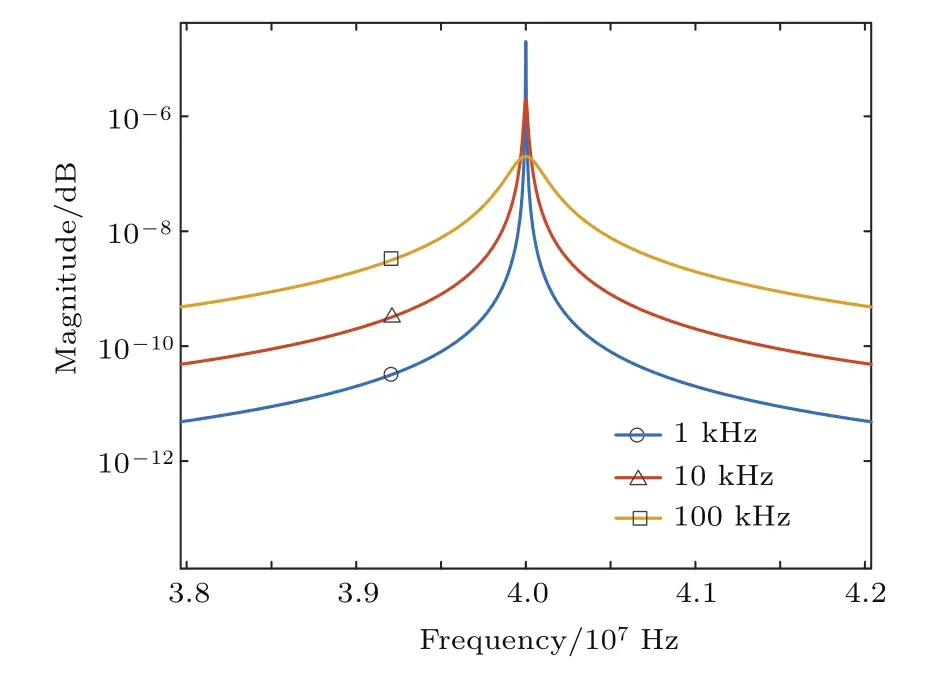
圖3 (網刊彩色)不同激光線寬的光電流譜線分布Fig.3.(color online)Photocurrent frequency spectral line distribution of different laser width.

假定激光線寬一定(Δω=100 kHz),探測距離分別為2,10,20 km,α=0.1,中頻頻率ωs=40 MHz,代入(19)式中可得光電流譜線分布如圖4所示.觀察圖4可知,探測距離越大,光電流譜線線型接近洛倫茲線型,且光電流譜線的半高全寬與探測距離無確定關系,即延遲時間τd大于相干時間τc時外差探測系統的探測距離對探測器輸出信號的功率譜分布情況影響不大.

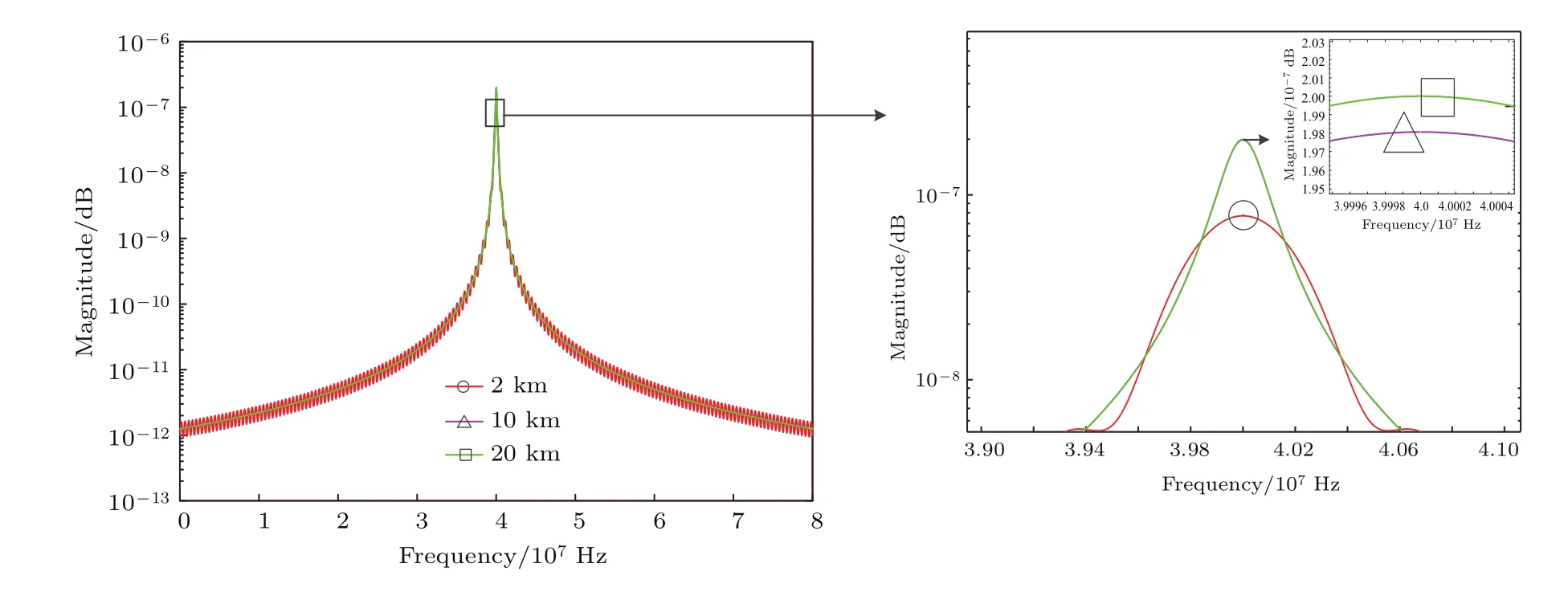
圖4 (網刊彩色)不同探測距離下光電流譜線分布Fig.4.(color online)The photocurrent frequency spectral line distribution of different detection distance.

2)延遲時間小于相干時間

當延遲時間小于相干時間時,仿真參數激光線寬分別為1,10,100 kHz,探測距離d=100 m,兩路光的振幅之比α=0.1,聲光調制器的頻率ωs=40 MHz,激光平均波長λ=532 nm.將上述仿真參數代入(17)式中,可得圖5不同激光線寬的光電流譜線分布.可見當探測距離相同時,激光線寬只影響光電流譜線分布的幅值大小,對光電流譜線的半高全寬的影響不大.但由于本底噪聲的存在,激光線寬越小,中頻信號與本底噪聲的幅頻差值越大,即中頻信號的提取越容易.

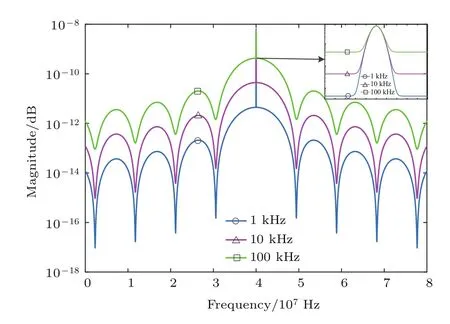
圖5 (網刊彩色)不同激光線寬的光電流譜線分布Fig.5.(color online)Photocurrent frequency spectral line distribution of different laser width.

若仿真參數激光線寬Δω=10 kHz保持不變,探測距離分別為10,100,1000 m,兩路光的振幅之比α=0.1,聲光調制器的頻率ωs=40 MHz,將上述參數代入(19)式中,可得圖6不同探測距離下光電流譜線分布.可見探測距離越小,光電流信號的頻譜越精細,即中頻信號的檢測越容易.由(33)式也可以看出探測距離越小,可以探測到的光學極限位移分辨率越小.

近距離下激光外差探測光學極限位移分辨率如(33)式所示,假設激光平均波長λ=532 nm,探測器光電轉換效率因子ε=0.5,激光線寬Δω=分別為1,10,100 kHz,探測距離最大到200 m,仿真結果如圖7所示.可知當激光線寬在1 kHz,探測距離為典型值100 m時,光學極限位移分辨率sn為0.266 nm.

綜上所述,外差探測系統中探測器輸出信號的功率譜分布與激光線寬、探測距離、延遲時間有直接聯系.當延遲時間τd大于相干時間τc時,激光線寬越小,探測距離越大光電流的譜線分布越接近洛倫茲型,光電流譜線的半高全寬只取決于激光線寬.當延遲時間τd小于相干時間τc時,激光線寬越小,中頻信號的提取越容易.同時由光學極限位移分辨率仿真結果可知,激光線寬越小,探測距離越小,外差系統的極限位移分辨率越小,與理論推導結論相符合.對于激光外差探測技術,激光光源的選擇對實際探測結果存在很大影響,具體表現在測量結果的精準度上.根據以上結果,針對位移分辨率要求不同的外差系統,可以參考理論推導公式選擇合適的激光光源,這對于工程應用和節省經費開支是很有意義的.

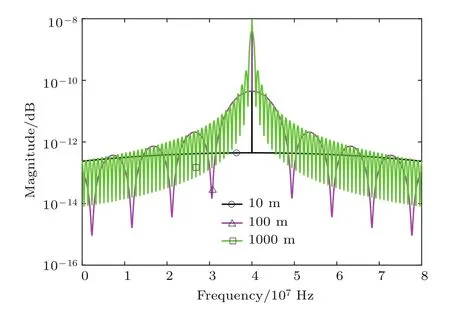
圖6 (網刊彩色)不同探測距離下光電流譜線分布Fig.6.(color online)Photocurrent frequency spectral line distribution of different detection distance.

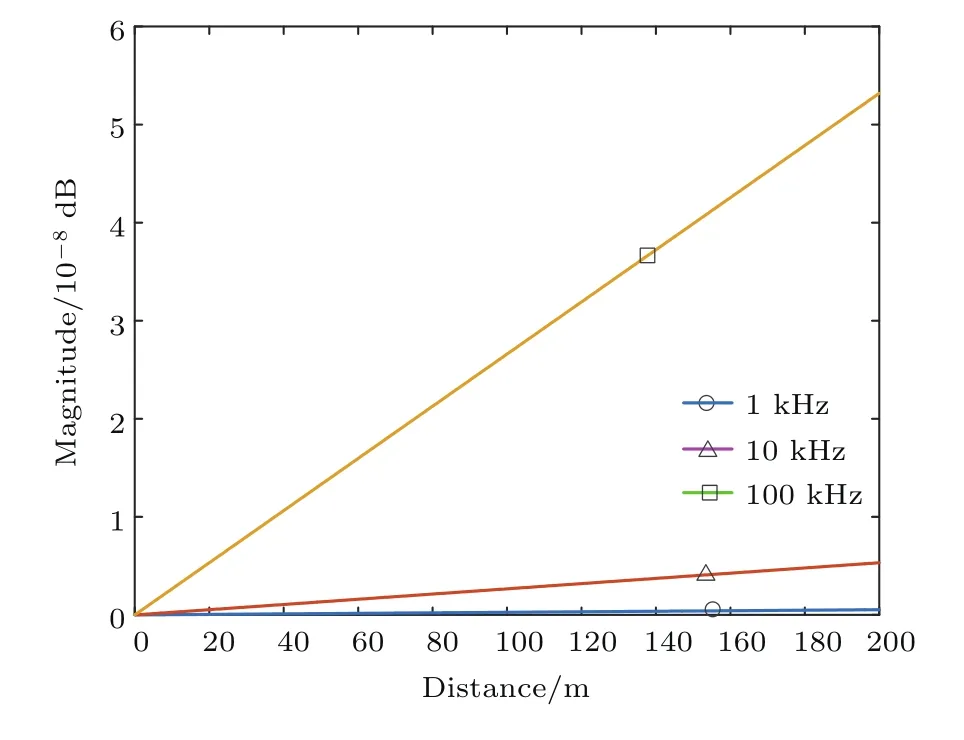
圖7 不同激光線寬下極限位移分辨率隨探測距離的變化Fig.7.Limited displacement resolution varies with the detection distance under different laser linewidth.

4 結 論

通過理論推導得到了激光外差探測系統探測器輸出信號的功率譜函數,修正了相關文獻中的功率譜函數公式,獲得了近距離外差探測系統光學極限位移分辨率的理論公式,并進行了數值仿真.數值仿真結果表明,不管延遲時間τd和相干時間τc處于哪種關系,激光光源的線寬越小,中頻信號的提取越容易,即外差系統可探測的光學極限位移越小;當延遲時間τd小于相干時間τc時,探測距離越小,外差系統的極限位移分辨率越小,這與光學極限位移的理論推導公式相符合.當外差探測系統參數均為典型值時,即探測器光電轉換效率因子ε=0.5,激光波長λ=532 nm,探測距離為100 m,激光線寬Δω=1 kHz,此時外差探測光學極限位移分辨率為0.266 nm.在工程應用中,數值分析的結果可以為不同需求的外差探測系統提供理論支持,尤其是外差探測系統極限位移分辨率對激光波長、激光線寬以及探測距離的要求.

[1]Kingston R 1977Opt.News3 27

[2]Swanson E A,Carter G M 1989Appl.Opt.28 3918

[3]Mosley D E,Matson C L,Czyzak S R 1998Aerospace Defense Sensing and Controls3380 243

[4]Nan J D,Pi M J,Fan L M 1989Acta Opt.Sin.10 714(in Chinese)[南京達,皮名嘉,樊立明,李洪濱 1989光學學報10 714]

[5]Pu L L,Zhou Y,Sun J F,Shen B L,Lu W 2011Acta Opt.Sin.31 260(in Chinese)[濮莉莉,周煜,孫劍鋒,沈寶良,魯偉2011光學學報31 260]

[6]Shintaro H,Yuki K,Ryosuke N,Norio H,Tadao N 2015Opt.Express23 26689

[7]Luo Y,Feng G Y,Liu J,Zhou C Y,Zhou S H 2014Chin.J.Lasers41 1108001(in Chinese)[羅韻,馮國英,劉建,周晟陽,周壽桓2014中國激光41 1108001]

[8]Luo H J,Yuan X H 2013Chin.J.Lasers40 173(in Chinese)[羅韓君,元秀華 2013中國激光 40 173]

[9]Li C Q,Wang T F,Zhang H Y,Xie J J,Liu L S,Guo J 2016Acta Phys.Sin.65 084206(in Chinese)[李成強,王挺峰,張合勇,謝京江,劉立生,郭勁 2016物理學報 65 084206]

[10]Shang J H,Zhao S G,He Y,Chen W B,Jia N 2011Chin.Opt.Lett.9 081201

[11]An Y Y,Liu J F,Li Q H 2007Optoelectronic Technology(2nd Ed.)(Beijing:Publishing House of Electronics Inducstry)p167(in Chinese)[安毓英,劉繼芳,李慶輝2007光電子技術(第二版)(北京:電子工業出版社)第167頁]

[12]Wang Y D,Wang J 2011Fundamentals of Random Signal Analysis(3rd Ed.)(Beijing:Publishing House of Electronics Inducstry)(in Chinese)[王永德,王軍 2011隨機信號分析基礎(第三版)(北京:電子工業出版社)]

[13]Rowe H E 1965Signal and Noise in Communication Systems(Princeton,NJ:van Nostrand)

[14]Gallion P B,Debarge G 1984IEEE J.Quantum Electron.20 343

[15]Yves P,Michel P,Michel M,Michel T 2009Opt.Express17 3659

[16]Siegman A E,Benedetto D,Manes K R 1967IEEE J.Quantum Electron.3 180

[17]Wolfgang Osten 2007Optical Inspection of Microsystems(1st Ed.)(New York:CRC Press)p246

[18]Dandridge A,Tveten A B 1982Opt.Lett.7 279

Short-range optical limited displacement resolution in laser heterodyne detection system?

Yan Chun-Hui1)2)Wang Ting-Feng1)?Zhang He-Yong1)Lü Tao1)2)Wu Shi-Song1)2)

1)(State Key Laboratory of Laser Interaction with Matter,Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China)
2)(University of Chinese Academy of Sciences,Beijing 100049,China)

23 June 2017;revised manuscript

8 August 2017)

Photocurrent power spectral density function of laser heterodyne detection is obtained by the statistical theory and Wiener-Khinchin theorem.For a short-range distance heterodyne system without considering atmospheric turbulence,we observe the relations between the photocurrent spectral line distribution and the laser linewidth,the intermediatefrequency signal,and the propagation delay time of signal light relative to local oscillator light.Theoretical formula of photocurrent power spectrum in relevant papers is revised to eliminate the effect of laser linewidth.Onedimensional probability distribution model of phase noise caused by laser linewidth is built based on the signal and noise theory.Accordingly we establish a mathematical model of limit detection accuracy based on laser wavelength,detection distance,and laser linewidth,which indicates the minimum detectable amplitude of heterodyne system.According to the numerical results,we find that the distribution of photocurrent spectral line intensities is greatly dependent on the relation between delay time and coherent time.And the minimum resolvable displacement increases with the detection distance and laser line width increasing.When the optical limited displacement resolution is 0.266 nm with a laser wavelength of 532 nm,a laser line width is 1 kHz,and a detection distance is 100 m.Experimental data in relevant papers agree well with the theoretical derivations.Our findings show that the research of displacement resolution might provide a quantitative reference for the theoretical research and engineering application of short-range heterodyne resolution.

laser Doppler velocimeters,laser applications,lasers

PACS:42.79.Qx,42.62.–b,42.55.–fDOI:10.7498/aps.66.234208

*Project supported by the Key Research Program of Frontier Science,Chinese Academy of Sciences(Grant No.QYZDBSSW-SLH014)and the Yong Scientists Fund of the National Natural Science Foundation of China(Grant No.61205143).

?Corresponding author.E-mail:tingfeng_w@sina.com

(2017年6月23日收到;2017年8月8日收到修改稿)

通過統計理論和維納-辛欽定理推導出激光外差探測系統光電流的功率譜函數,分析了光電流譜線分布與激光光源線寬、中頻信號頻率以及信號光相對本振光傳輸延遲時間的關系,修正了相關文獻中光電流功率譜的理論公式.根據信號與噪聲理論建立了激光線寬引起的相位噪聲的一維概率分布模型,并據此得到了基于激光波長、探測距離以及激光線寬的極限位移分辨率的數學模型.對光電流的功率譜和外差光學極限位移分辨率進行了相關的數值仿真,結果表明延遲時間與相干時間的關系決定光電流譜線分布的情況.當激光波長為532 nm,激光線寬在1 kHz,探測距離為100 m時,光學極限位移分辨率為0.266 nm,相關文獻中的實驗數據與理論推導結果相符合.

10.7498/aps.66.234208

?中國科學院前沿科學重點研究計劃(批準號:QYZDB-SSW-SLH014)和國家自然基金青年科學基金(批準號:61205143)資助的課題.

?通信作者.E-mail:tingfeng_w@sina.com