二維氫原子中的基態奇異特性數值精確對角化法?

劉褚航 強百強 季育琛 李煒

1)(上海科技大學物質科學與技術學院,上海 201210)

2)(中國科學院上海微系統與信息技術研究所,信息功能材料國家重點實驗室,上海 200050)

二維氫原子中的基態奇異特性數值精確對角化法?

劉褚航1)強百強1)季育琛1)李煒2)?

1)(上海科技大學物質科學與技術學院,上海 201210)

2)(中國科學院上海微系統與信息技術研究所,信息功能材料國家重點實驗室,上海 200050)

二維氫原子,離散貝塞爾基函數,Lanczos法

1 引 言

隨著計算機技術的發展,數值精確對角化法在現代計算凝聚態物理學中扮演著至關重要的角色[1],尤其是在強關聯電子體系的研究領域中,它已成為其他數值計算技術的參照,盡管數值精確對角化法存在著其只能處理較小的物理系統的局限性.另外,可以通過幺正變換改變基函數的選取,以及通過對稱性的約束來極大程度地提高計算體系的尺寸[2],比如通過傅里葉變換將實空間中的哈密頓量變換到動量空間[3],從而改變基函數的選取來處理具有平帶特性[4?6]的分數拓撲量子態的新奇特性[7?9],以及極大程度地提高數值計算量和所計算體系的尺寸大小[10,11].

通過幺正變換改變基函數的選取在量子力學中被稱為表象變換[12,13].選擇合適的表象會讓人們對物理系統的圖像有更清晰的認識,比如對于自由運動的粒子,在動量表象下它的本征能譜是對角化的;對于超導體中的電子Copper配對,在Bogoliubov表象下它的本征能譜也是對角化的[14].

在本文中,我們利用表象變換選取合適的貝塞爾函數為基函數,再利用Lanczos技術[15]數值精確對角化處理在維度受限下的二維氫原子基態的奇異行為,得到的數值基態波函數與解析結果完全符合.構造這套具有正交性、歸一化、完備的離散貝塞爾基函數,將有助于今后研究一些波函數具有數值奇異特性的體系中發揮重要作用;同時,與這套離散貝塞爾基函數相類似的線性綴加平面波的基函數,在基于密度泛函理論框架下的第一性原理計算模擬中也扮演著重要的角色[16,17].

本文討論了利用解析和數值有限差分法計算三維氫原子的本征能級及其相應的本征波函數,所得到的解析結果與數值結果相一致.這說明數值有限差分法在三維氫原子體系中的合理適用性.同時,進一步推廣數值有限差分法到維度受限下的二維氫原子體系,計算發現對于基態波函數所得的解析結果與數值結果不一致,但是對于其他激發態的徑向波函數解析和數值計算所得的結果卻相一致.這說明二維氫原子體系的基態波函數存在著數值奇異特性.該奇異特性主要體現在基態的徑向波函數R(r)隨著r趨于0時,簡化的徑向波函數將趨于有限值,而不再是0.為了在數值上克服該奇異特性,引入一套新的具有軸向對稱性的離散貝塞爾基函數,并將徑向波函數R(r)用這套新的離散貝塞爾基函數做線性展開,同時利用數值Lanczos技術精確對角化獲得了體系基態能量與基態波函數,與解析結果完全一致.

2 三維氫原子模型的解析和數值有限差分法求解

2.1 模型解析求解

對于三維氫原子的定態薛定諤方程可表示為[13]

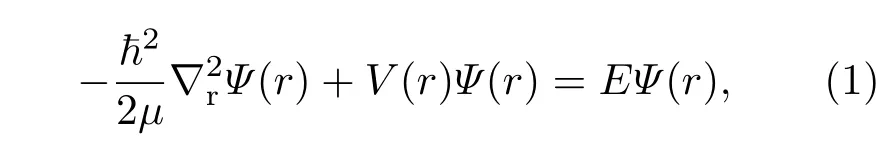
其中?為約化普朗克常數,μ為折合質量,V(r)=?e2/r為三維氫原子的中心勢能,E為體系的本征能量,其相應的本征波函數為Ψ(r).考慮到體系的庫侖能具有中心球對稱性,可以將本征波函數Ψ(r)用球諧函數Ylm(θ,φ)為基做線性展開[18],即

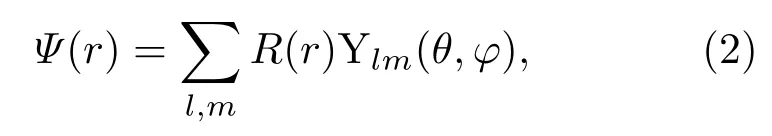
其中R(r)為展開系數,稱之為徑向波函數,代入到定態薛定諤方程(1),于是得到關于在三維氫原子的中心勢場下的徑向波函數R(r)所滿足的微分方程為

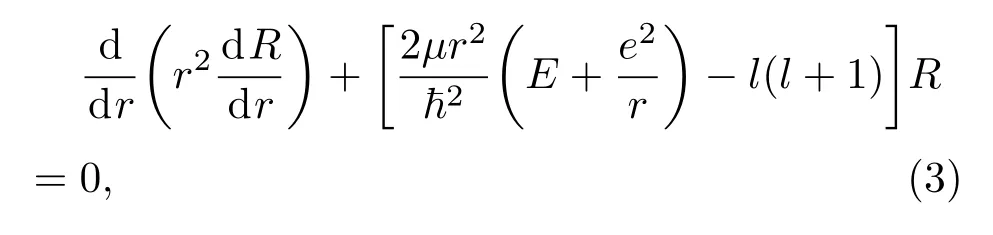
其中l=0,1,2,···稱為軌道角動量量子數.引入函數變量代換R(r)=u(r)/r,并代入到微分方程(3),化簡得到關于u(r)的微分方程為

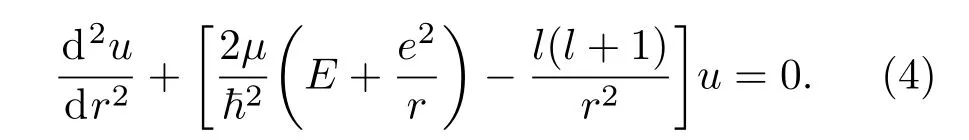
可以較為容易地通過冪級數展開法[19]嚴格解析求得徑向波函數Rnl(r)的解析表達形式及其相對應的本征能量這里n稱為主量子數.在l=0時,前三個本征態的徑向波函數Rnl(r)的解析形式分別為:

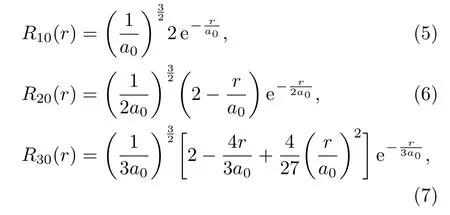
2.2 數值有限差分法

采用數值計算方法來求解徑向波函數u(r)所滿足的微分方程(4),即利用數值離散差分法化簡微分方程(4),并得到差分方程[20]為

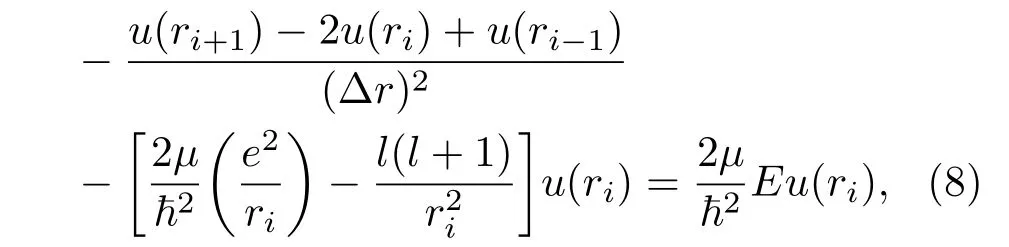
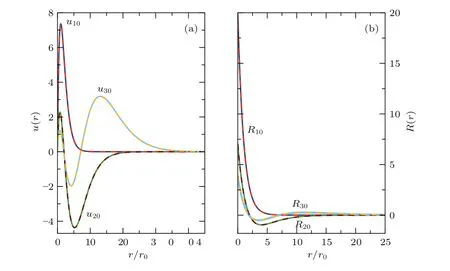
圖1 三維氫原子徑向波函數 (a)u(r)和(b)R(r)的解析(實線)和數值有限差分法(虛線)所得到的結果Fig.1.Radial wave function of the three-dimensional hydrogen atom for u(r)in(a)and R(r)in(b)by using an analytical(solid line)and numerical(dashed line)methods.

其中Δr為離散化的兩個格點之間的距離.為求解差分方程(8),首要考慮的是邊界條件.考慮到徑向波函數u(r)隨著r趨于+∞時,徑向波函數u(r)將趨于0,以及徑向波函數u(r)隨著r趨于0時,徑向波函數u(r)也將趨于0;同時,結合差分方程(8),可很容易通過數值精確對角化法精確地求解差分方程(8),并得到體系的本征能量及其相應的本征波函數.從圖1可以很清楚地看到,對于三維氫原子的徑向波函數u(r)和R(r)的解析結果與數值有限差分法所得的結果完全符合,相應的本征能量也完全符合,即解析和數值解得的基態能量均為E1=?13.625 eV.

3 二維氫原子模型的解析和數值有限差分法求解

3.1 模型解析求解

下面討論二維氫原子情況,即在維度受限下的二維氫原子的定態薛定諤方程可表示為

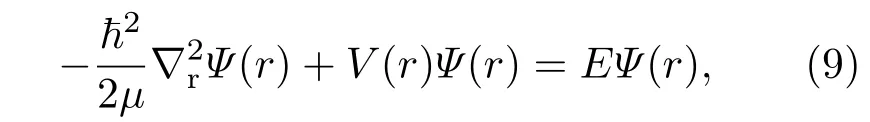
其中勢能V(r)=?e2/r,它已不再具有三維球對稱性,而是具有平面軸對稱性[18].因此,可以將波函數Ψ(r)用軸向波函數eimθ為基做線性展開,即

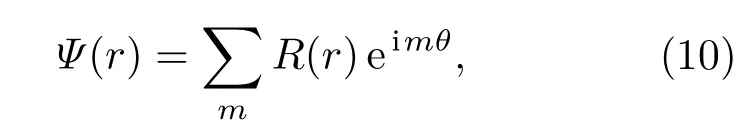
其中m=0,±1,±2,···稱為磁量子數,它是角動量l在z方向上的投影算符lz的本征值,即算符lz的本征方程為

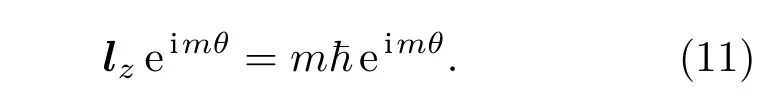
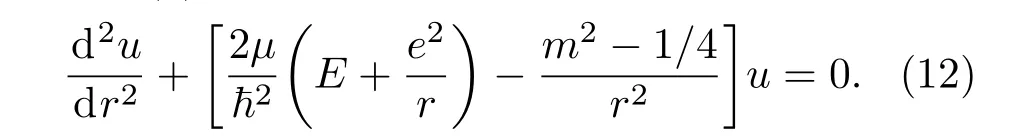
相比三維氫原子的徑向波函數u(r)所滿足的微分方程(4)而言,可以很清楚地看到兩者微分方程的形式是極為相似的,但是對于基態所滿足的微分方程,即l=0的三維氫原子和m=0的二維氫原子的微分方程卻有著本質的區別,它將會給二維氫原子的基態行為帶來諸多奇異性質.

同樣地,類似于三維氫原子的冪級數展開解法[19]也很容易地通過冪級數展開法解析求得二維氫原子的徑向波函數Rnm(r)的解析表達形式及其相對應的本征能級

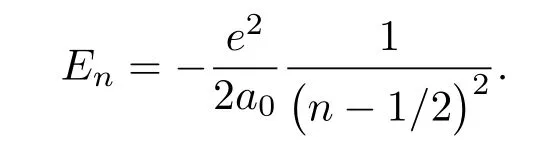
3.2 數值有限差分法

采用數值有限差分法數值求解二維氫原子的徑向波函數u(r)所滿足的微分方程(12)式,并得到離散差分方程[20]為

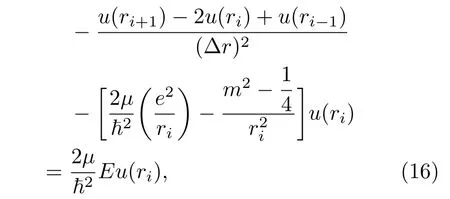
其中Δr為離散化的兩個格點之間的距離.為求解差分方程(16),同樣需要考慮體系的邊界條件.如果依然假設徑向波函數u(r)隨著r趨于+∞時,徑向波函數u(r)將趨于0,以及徑向波函數u(r)隨著r趨于0時,徑向波函數u(r)也將趨于0;同時,結合差分方程(16),可很容易地通過數值精確對角化法求解差分方程(16)并得到體系的本征能量及其相對應的本征波函數.如圖2所示,體系在m/=0時的激發態徑向波函數unm(r)的解析結果均與數值有限差分法所獲得的結果完全符合,但是對于基態徑向波函數u10(r),數值有限差分法的結果與解析結果卻不一致,同時其相應的本征能量也不一致,即解析解得的基態本征能量為E1=?54.4 eV,而數值有限差分法所解得的基態本征能量為E1=?2214.6 eV.這說明數值有限差分法已不再適用于處理二維氫原子的基態本征值問題.其原因是對于二維氫原子的基態徑向波函數u10(r),隨著r趨于0時,u10(r)趨于有限值,而不再是零,它與三維氫原子的情形截然不同.出現這樣的問題,本質上是源于有限差分方法在處理邊界條件問題上存在著局限性,即無法處理具有非零特性的第一類邊界條件的微分方程.因此,需要尋找其他數值技術來克服這類問題,比如可以采用貝塞爾函數為基函數做線性展開進行處理[19].

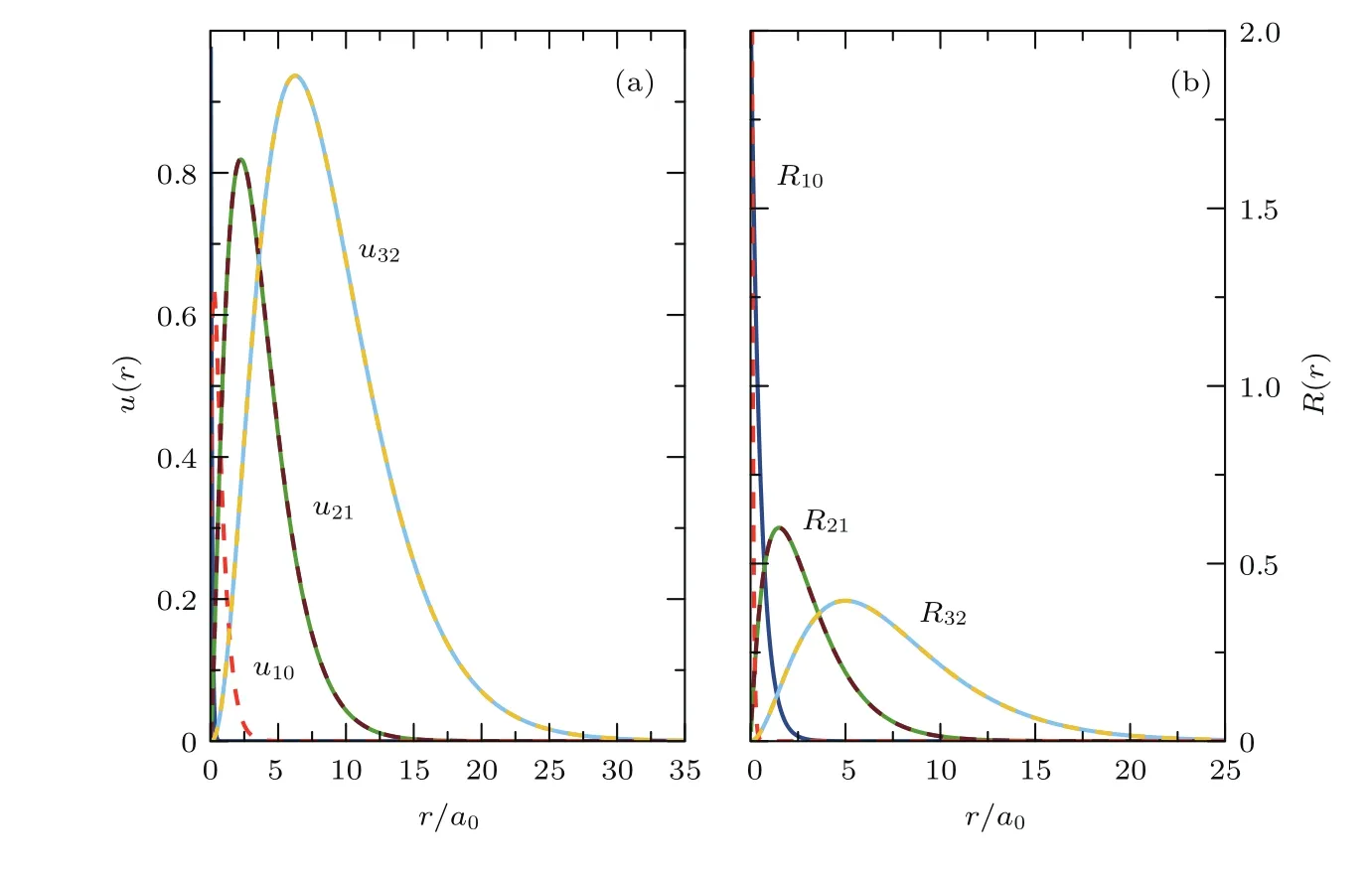
圖2 二維氫原子徑向波函數 (a)u(r)和(b)R(r)的解析(實線)和數值有限差分法(虛線)所得到的結果Fig.2.Radial wave function of the two-dimensional hydrogen atom for u(r)in(a)and R(r)in(b)by using an analytical(solid line)and numerical(dashed line)methods.

4 以貝塞爾函數為基函數做線性展開的數值精確對角化法

4.1 討論二維氫原子的徑向波函數u(r)在r=0處的漸近行為

以上數值有限差分法的計算結果表明,對于有限差分法已不再適用于處理具有數值奇異特性的二維氫原子體系的基態波函數行為,即本征波函數u10(r)的特征.因此,可以采用另一套數值方法,即將本征波函數用一套具有正交完備性的函數為基函數做線性展開,以此來數值求解此體系的微分方程.考慮到二維氫原子系統具有軸向對稱性,可以選用貝塞爾函數為基函數[19].由于貝塞爾函數種類很多,可根據體系的漸近行為,選擇一套合適的正交基.首先討論球貝塞爾函數,它的正交性為[19]

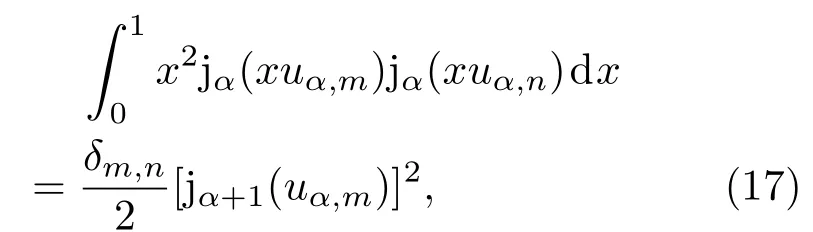
其中α為球貝塞爾函數的階,uα,m為α階的球貝塞爾函數的第m個零點.根據基函數的正交特性,可以得到一套正交基為:另外,根據前面的解析計算可知,當m=0時,二維氫原子的徑向波函數R(r)在r=0處是一個不為零的有限值.因此,徑向波函數u(r)在r=0處的漸近行為必須滿足形式.如果這里選用以球貝塞爾函數為正交完備基,那么徑向波函數u(r)在r=0處的漸近行為將與r相同,這會導致所計算出來的徑向波函數R(0)=0,依然與解析計算結果不一致.因此,當且僅當正交基函數在r=0處的漸近行為滿足形式時,徑向波函數R(0)的行為才符合解析結果的特性.能滿足這種特性的是貝塞爾函數.如果我們考慮貝塞爾函數的連續正交基,其正交關系為[19]

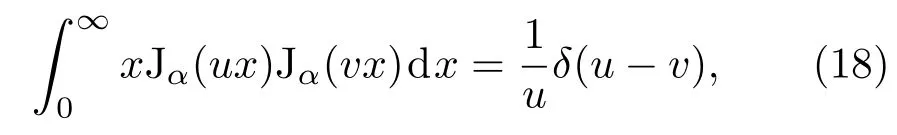
它的積分區間為無窮大,而且還是具有連續變化的基函數,它將不利于數值計算.因此,改用貝塞爾函數的離散正交基,其正交關系為[19]

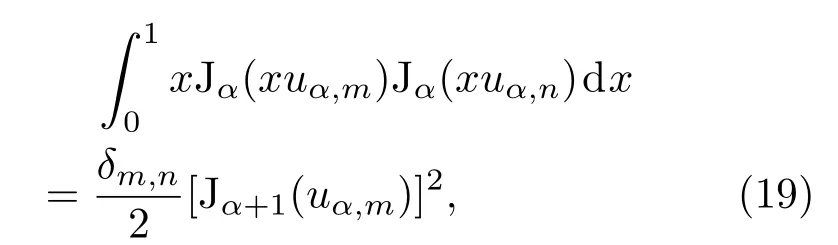
其中α為貝塞爾函數的階,uα,m為α階貝塞爾函數的第m個零點.根據正交關系,可很容易地得到一套新的正交完備基為若取α=0,即若選取零階貝塞爾函數為離散正交基,那么在r=0處,徑向波函數R(r)的漸近行為剛好符合形式.

4.2 基于Lanczos技術的數值精確對角化法

根據上述討論的徑向波函數的漸近行為,可以將零階貝塞爾函數的離散正交基表示為fm:

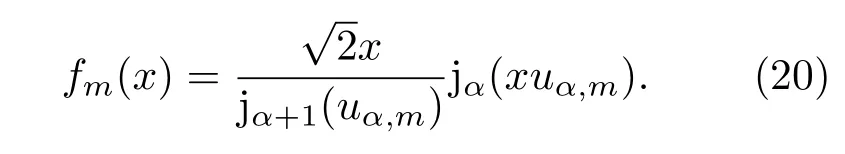
然后進行變量代換x=y/b,則新的基函數在區間[0,b]上滿足正交性,適合于數值求解.通過基的幺正變換后,得到體系的哈密頓量在基函數hm下的矩陣元為

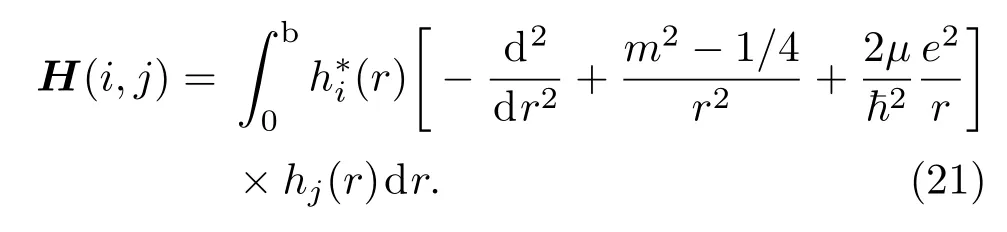
可以通過Lanczos方法[15]數值精確對角化體系的哈密度量H的矩陣元(21)式并得到在基函數hm下的本征矢量v及其相應的本征能量.最終求得二維氫原子的徑向波函數u(r)為

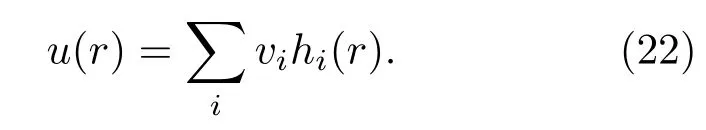
在數值計算過程中,選取有限個hi(i=1,2,···,N)作為假想的完備性基函數,其中N為基函數的截斷值.理論上,隨著選取的截斷值N趨于無窮大,基函數hi接近于完備性.但是在實際的數值計算過程中需要對N做截斷.截斷的合理性根據誤差ΔE來確定,即ΔE=En1?Ea1,其中En1表示為數值精確對角化求得的基態能量,而Ea1則表示為解析求得的基態能量.如圖3(a)所示,可以清楚地看到隨著截斷值N的增大,誤差ΔE將快速地趨于零.當N=7000時誤差已經小于0.005.同時,在N=7000時,還計算了體系的徑向波函數u10(r)和R10(r),如圖3(b)所示,與解析結果完全一致.

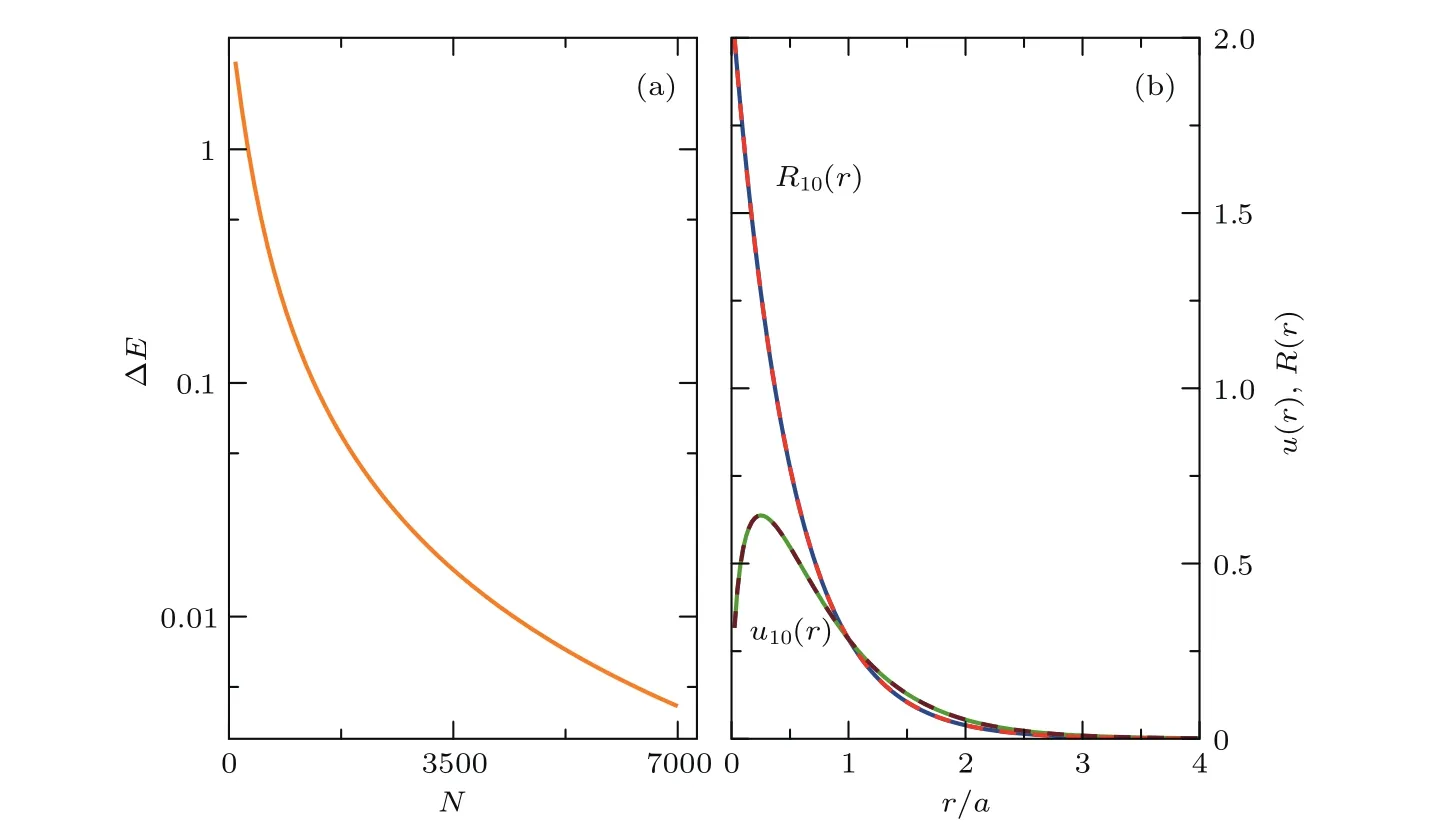
圖3 (a)數值計算的基態本征值與理論值之間的誤差隨基函數個數的關系;(b)基態徑向波函數u(r)和R(r)的解析(實線)與數值有限差分法(虛線)所得到的結果Fig.3.(a)Error ΔE between numeral(En0)and analytical(Ea0)results for the ground state of twodimensional hydrogen system;(b)radial wave function of the two-dimensional hydrogen atom for u(r)and R(r)by using an analytical(solid line)and numerical(dashed line)methods for the ground state.

5 結 論

討論了利用解析和數值有限差分法分別計算三維氫原子和二維氫原子的本征能級及其相應的本征波函數,計算發現由于在維度受限下的二維氫原子體系的基態波函數存在著數值奇異特性.為了解決該數值奇異性,構造了一套新的離散的貝塞爾函數為基函數做線性展開,同時結合數值Lanczos精確對角化法,最終獲得體系基態能量和基態波函數均與解析相一致的結果.這套新的完備的離散貝塞爾基函數的構造可以在研究一些波函數具有數值奇異特性的體系中發揮至關重要的作用.

[1]Fehske H,Schneider R,Weibe A 2008Computational Many-Particle Physics(Berlin:Springer)p529

[2]Lin H Q 1990Phys.Rev.B42 6561

[3]Regnault N,Bernevig B A 2011Phys.Rev.X1 021014

[4]Tang E,Mei J W,Wen X G 2011Phys.Rev.Lett.106 236802

[5]Sun K,Gu Z C,Katsura H,Sarma S D 2011Phys.Rev.Lett.106 236803

[6]Neupert T,Santos L,Chamon C,Mudry C 2011Phys.Rev.Lett.106 236804

[7]Sheng D N,Gu Z C,Sun K,Sheng L 2011Nat.Commun.2 389

[8]Li W,Liu Z,Wu Y S,Chen Y 2014Phys.Rev.B89 125411

[9]Li W,Sheng D N,Ting C S,Chen Y 2014Phys.Rev.B90 081102(R)

[10]Li W,Chen Y 2016EPL113 47001

[11]Liu C R,Guo Y W,Li Z J,Li W,Chen Y 2016Sci.Reports6 33472

[12]Dirac P A M 1982The Principles of Quantum Mechanics(Oxford:Oxford Science Publications)p53

[13]Shankar R 1994Principles of Quantum Mechanics(New York Plenum Press)p115

[14]Bardeen J,Cooper L,Schriffer J R 1957Phys.Rev.8 1178

[15]Lanczos C 1950J.Res.Nat.I Bur.Std.45 255

[16]Hohenberg P,Kohn W 1964Phys.Rev.136 B864

[17]Singh D 1994Planewaves,Pseudopotentials and the LAPWMethod(Boston/Dordecht/London: Kluwer Academic Publishers)p43

[18]Dresselhaus M S,Dresselhaus G,Jorio A 2008Group Theory Application to the Physics of Condensed Matter(Springer)p57

[19]Wang Z X,Guo D R 2012Introduction to the Special Functions(Beijing:Peking University Press)p381(in Chinese)[王竹溪,郭敦仁 2012特殊函數概論 (北京:北京大學出版社)第381頁]

[20]Ma W T 2016Computational Physics(Beijing:Science Press)p64(in Chinese)[馬文淦 2016計算物理學 (北京:科學出版社)第64頁]

Numerical exact diagonalization of singularity in the ground state of two-dimensional hydrogen atom?

Liu Chu-Hang1)Qiang Bai-Qiang1)Ji Yu-Chen1)Li Wei2)?

1)(School of Physical Science and Technology,ShanghaiTech University,Shanghai 201210,China)
2)(State Key Laboratory of Functional Materials for Informatics,Shanghai Institute of Microsystem and Information Technology,Chinese Academy of Sciences,Shanghai 200050,China)

6 July 2017;revised manuscript

13 August 2017)

With the development of computing technology,numerical exact diagonalization method plays a vital role in modern computational condensed matter physics,especially in the research area of strongly correlated electron systems:it becomes a benchmark for other numerical computational techniques,such as quantum Monte Carlo,numerical renormalization group,density matrix renormalization group,and dynamic mean field theory.In this paper,we first numerically exactly diagonalize the three-dimensional hydrogen atom with the combination of finite-difference method,and find that the numerical wave function of ground state is in good agreement with the analytical calculations.We then turn to discuss the space dimension confinement hydrogen system,two-dimensional hydrogen atom,and notice that the numerical wave function is no longer in agreement with the analytical calculation,where the ground state wave function has a numerical singularity as radius approaches to zero.Compared with the case of the three-dimensional hydrogen atom,this issue mainly comes from the nature of space dimension confinement.To resolve such an issue of numerical singularity in two-dimensional hydrogen atom,we need to construct a new discrete and normalized Bessel function as a basis to study the ground state behavior of dimension confinement system based on the framework of Lanczos-type numerical exact diagonalization.The constructed normalized Bessel basis is orthogonal and discrete,and thus becomes suitable for practical calculation.Besides,these prominent properties of such a Bessel basis greatly reduce the complexity and difficulty in practical calculation,and thus makes computing work efficient.In addition,Lanczos-type numerical exact diagonalization method can extremely speed up the process of solving the eigenvalue equation.As a result,such a high efficient calculation of our method demonstrates the consistence between numerical and analytical ground state energy value,and the corresponding wave function with enough truncated basis number.Since this kind of numerical singularity occurs in many space dimension confinement systems,our finding for constructing a new discrete Bessel basis function may be helpful in studying the quantum systems with numerical singularity behaviors in wavefunctions in future.On the other hand,it should be pointed out that the Bessel basis is incorporated into the linear augment plane wave method in the density functional theory to study the electronic band structure of the condensed material and obtain high accurate results,especially in the theoretical prediction of topological insulators and in experimental realization as well.

two-dimensional hydrogen atom,discrete Bessel basis function,Lanczos-type numerical exact diagonalization

PACS:01.40.Fk,03.65.Ge,03.67.LxDOI:10.7498/aps.66.230102

*Project supported by the National Natural Science Foundation of China(Grant No.11404359)and the Youth Innovation Promotion Association of the Chinese Academy of Sciences(Grant No.2016215).

?Corresponding author.E-mail:liweiphysics@gmail.com

(2017年7月6日收到;2017年8月13日收到修改稿)

利用數值有限差分法處理二維氫原子的基態波函數時,計算結果發現其存在著數值奇異特性.本文通過構造一套具有正交完備性的離散貝塞爾基函數,并結合基于Lanczos技術的數值精確對角化方法研究二維氫原子中的基態波函數的數值奇異特性,得到的波函數數值解及其相應的本征能量均與解析結果相一致.這套新的完備的離散貝塞爾基函數,可以在研究一些波函數具有數值奇異特性的體系中發揮至關重要的作用.

10.7498/aps.66.230102

?國家自然科學基金(批準號:11404359)和中國科學院青年創新促進會計劃(批準號:2016215)資助的課題.

?通信作者.E-mail:liweiphysics@gmail.com