利用金剛石氮-空位色心精確測(cè)量弱磁場(chǎng)的探索?

李路思 李紅蕙 周黎黎 楊炙盛 艾清

(北京師范大學(xué)物理學(xué)系,北京 100875)

利用金剛石氮-空位色心精確測(cè)量弱磁場(chǎng)的探索?

李路思 李紅蕙 周黎黎 楊炙盛 艾清?

(北京師范大學(xué)物理學(xué)系,北京 100875)

弱磁探測(cè),金剛石氮-空位色心,退相干

1 引 言

弱磁探測(cè),如地磁場(chǎng)的精確測(cè)量,在航天、航空、航海導(dǎo)航以及遠(yuǎn)程精確制導(dǎo)等方面有重要意義.目前測(cè)量弱磁場(chǎng)的超靈敏度磁力儀有霍爾探針掃描顯微鏡、磁力顯微鏡[1,2]、質(zhì)子磁力儀[2]、超導(dǎo)量子干涉儀等[2,3],但需要在特定條件(如低溫和高真空度)下進(jìn)行測(cè)量,且成本較高.研究發(fā)現(xiàn),鳥(niǎo)類的視網(wǎng)膜[4]、蠑螈的松果體[5]、蜜蜂的腹部等[6]器官內(nèi)含有磁感應(yīng)源.三叉神經(jīng)假說(shuō)和自由基對(duì)機(jī)理(RPM)[7,8]是解釋鳥(niǎo)類感磁原因的兩個(gè)主流假說(shuō)之一.文獻(xiàn)[9]用量子Zeno效應(yīng)解釋了自由基對(duì)反應(yīng)對(duì)磁場(chǎng)的依賴性;文獻(xiàn)[10]進(jìn)一步探討了自由基對(duì)的量子控制和糾纏作用;受這一假說(shuō)啟發(fā),文獻(xiàn)[11]提出用推廣的Holstein模型來(lái)描述這樣一類依賴于自旋的化學(xué)反應(yīng),這對(duì)弱磁場(chǎng)精確測(cè)量技術(shù)的發(fā)展具有重要借鑒意義.

金剛石氮-空位(NV)色心[12]的電子基態(tài)是一種自旋三重態(tài)系統(tǒng),具有易于初始化、易于讀取、易于操控、相干時(shí)間長(zhǎng)、常溫操作等優(yōu)點(diǎn)[13?16],這使得NV色心系統(tǒng)成為有望實(shí)現(xiàn)量子信息處理[17]和量子計(jì)算[18]的候選者之一.NV色心系統(tǒng)的應(yīng)用方向之一是作為高靈敏度探針進(jìn)行弱磁場(chǎng)精確測(cè)量[19?21].已有研究將NV色心系統(tǒng)用于蛋白質(zhì)分子中的單個(gè)核自旋的弱磁測(cè)量[22],但對(duì)于靜態(tài)弱磁場(chǎng)的精確測(cè)量則鮮少涉及.文獻(xiàn)[23]研究了NV色心退相干機(jī)理和周期性動(dòng)態(tài)解耦控制對(duì)NV色心系統(tǒng)退相干行為的影響,發(fā)現(xiàn)不同強(qiáng)度磁場(chǎng)下NV色心的退相干行為和時(shí)間不同,這啟發(fā)了一種探測(cè)弱磁場(chǎng)的新方法.

本文基于NV色心系統(tǒng)退相干時(shí)間[24,25]對(duì)外磁場(chǎng)大小和方向高度敏感的原理,探索一種能夠精確測(cè)量微弱靜磁場(chǎng)的新途徑.通過(guò)模擬13C原子含量為自然豐度、14N為高純度的金剛石環(huán)境,實(shí)現(xiàn)NV色心電子自旋與周?chē)?3C核自旋的耦合,探究不同磁場(chǎng)大小下耦合的退相干時(shí)間,確定退相干時(shí)間與外磁場(chǎng)大小之間的高靈敏度關(guān)系.只要通過(guò)光學(xué)方法監(jiān)測(cè)NV色心的退相干時(shí)間,即可間接確定NV主軸方向的磁場(chǎng)大小.改變NV色心主軸方向,可以實(shí)現(xiàn)待測(cè)靜態(tài)弱磁場(chǎng)的高精度三維測(cè)量.

2 NV色心

2.1 NV色心的物理性質(zhì)

金剛石氮-空位色心是金剛石晶體中的一種點(diǎn)缺陷結(jié)構(gòu).如圖1所示,當(dāng)金剛石中碳原子構(gòu)成的面心立方晶格的一個(gè)碳原子被氮原子所取代,且其近鄰有一個(gè)晶格空位時(shí),就形成了NV色心.氮原子與空位的連線方向即為NV主軸方向,即[111]軸.

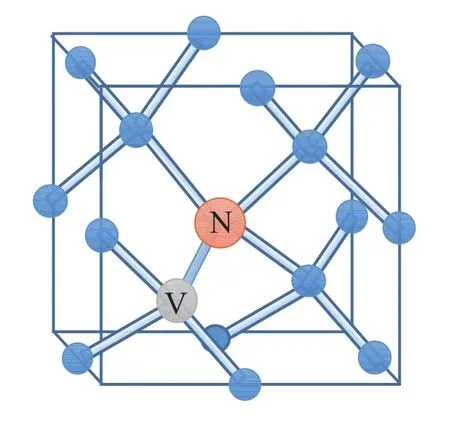
圖1 (網(wǎng)刊彩色)金剛石晶體中NV色心的物理結(jié)構(gòu)(橙色表示氮原子,灰色表示空位)Fig.1.(color online)Physical structure of the NV color center in diamond(the nitrogen atom and the vacancy are labeled by the orange sphere and the gray sphere,respectively).

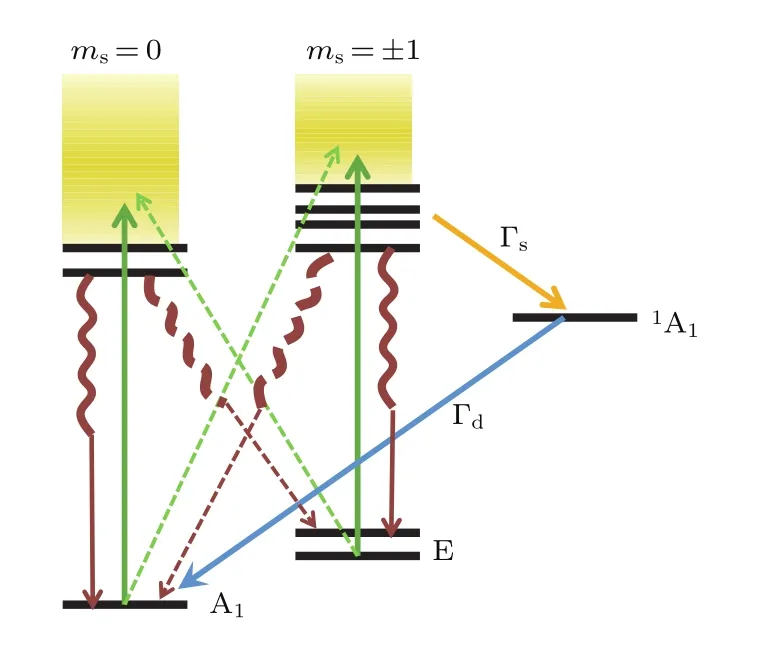
圖2 (網(wǎng)刊彩色)NV色心的能級(jí)結(jié)構(gòu)和躍遷Fig.2.(color online)Energy level structure and transitions of the NV center.

基態(tài)NV色心的總自旋S=1,對(duì)應(yīng)的能級(jí)結(jié)構(gòu)和躍遷如圖2所示.實(shí)線表示可進(jìn)行躍遷,虛線表示不可進(jìn)行躍遷,Γs和Γd表示無(wú)輻射躍遷.NV的基態(tài)是自旋三重態(tài)3A,自旋磁量子數(shù)ms=±1和ms=0之間存在Δ=2.87 GHz的零場(chǎng)劈裂.由于存在與聲子相關(guān)的無(wú)輻射躍遷(Γs和Γd),故可用激光脈沖來(lái)極化電子自旋至ms=0態(tài),即初始化.電子由激發(fā)態(tài)躍遷到基態(tài)時(shí)發(fā)出熒光光子,且由于躍遷過(guò)程不同,初始態(tài)為ms=0態(tài)的熒光強(qiáng)度比ms=±1態(tài)的熒光強(qiáng)20%—40%[26,27],由此可實(shí)現(xiàn)電子自旋狀態(tài)的讀出.

2.2 NV色心系統(tǒng)哈密頓量

金剛石中隨機(jī)分布著自旋為1/2的13C,NV色心電子自旋為1,會(huì)與13C核自旋通過(guò)磁偶極相互作用耦合.在外場(chǎng)B的作用下,整個(gè)系統(tǒng)的哈密頓量為[28,29]

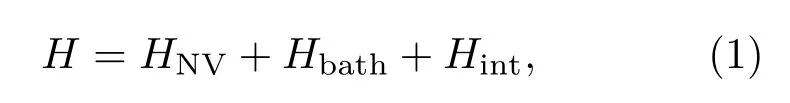
式中NV的哈密頓量HNV和13C環(huán)境的哈密頓量Hbath分別為

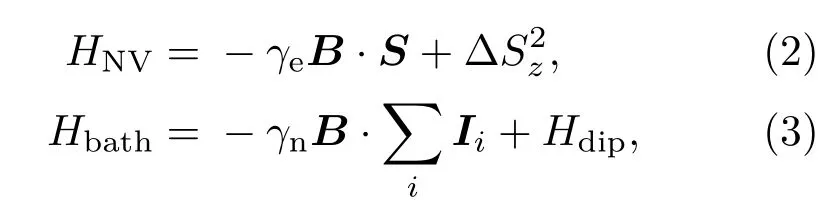
式中γe,γn分別為電子自旋和核自旋的旋磁比,Hdip描述核自旋之間的磁偶極相互作用,Ii為NV色心周?chē)?3C環(huán)境中第i個(gè)13C核的自旋角動(dòng)量算符.

(1)式中最后一項(xiàng)

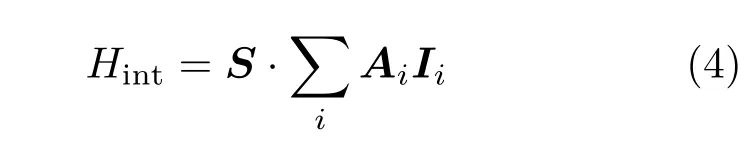
描述電子自旋與核自旋之間的相互作用,是造成NV退相干的主要原因,式中Ai為第i個(gè)近鄰核自旋與電子自旋之間的磁偶極相互作用.

故第i個(gè)核自旋的哈密頓量為

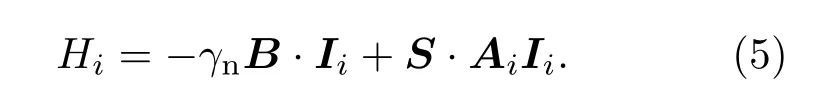
由于電子和核自旋之間大失諧,超精細(xì)相互作用不會(huì)誘導(dǎo)電子自旋的翻轉(zhuǎn),所以當(dāng)電子自旋處于|m〉態(tài)(m=0,±1為電子自旋的磁量子數(shù))時(shí),電子與核自旋的超精細(xì)耦合會(huì)為核自旋提供一個(gè)有效相互作用勢(shì),即核自旋的有效哈密頓量為

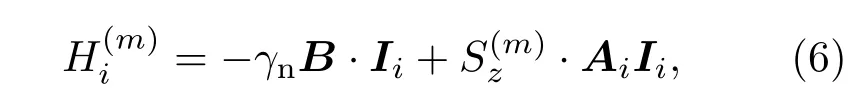
此時(shí)第i個(gè)核自旋受到的有效磁場(chǎng)為

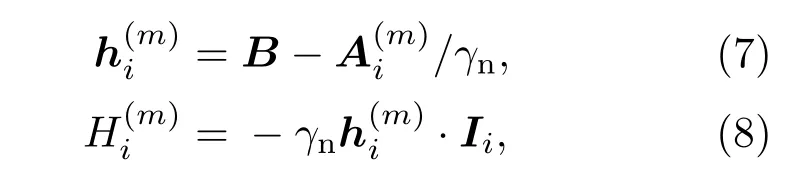
式中m=0,±1為電子自旋的磁量子數(shù),也即

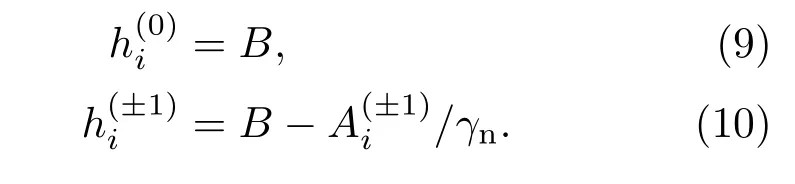
核自旋繞該有效磁場(chǎng)進(jìn)動(dòng),并對(duì)電子自旋產(chǎn)生調(diào)制.由于每個(gè)核所感受到的超精細(xì)耦合不同,各個(gè)13C核自旋的進(jìn)動(dòng)頻率也不同.對(duì)系統(tǒng)施加Hahn echo脈沖,可以有效消除這種差異,使得各核自旋對(duì)電子自旋的調(diào)制同時(shí)重相.但由于核自旋之間磁偶極相互作用的存在,并不能通過(guò)對(duì)系統(tǒng)施加Hahn echo脈沖來(lái)消除影響,因而引起了NV電子自旋|0〉態(tài)和|1〉態(tài)之間的退相干[30].

3 NV系統(tǒng)測(cè)量弱磁場(chǎng)

3.1 理論模擬

利用MATLAB對(duì)自然豐度(1.1%)13C環(huán)境中的NV色心系統(tǒng)在Hahn echo脈沖作用下的退相干過(guò)程進(jìn)行模擬,得到不同磁場(chǎng)強(qiáng)度下NV色心電子自旋|0〉態(tài)和|1〉態(tài)之間的退相干過(guò)程(圖3).在強(qiáng)、中、弱磁場(chǎng)條件下,NV色心退相干行為有顯著差異.該過(guò)程中有三個(gè)特征時(shí)間,即TW,TR,T2.其中TW為第一個(gè)半峰衰減到1/e的時(shí)間;TR為相鄰兩峰之間的時(shí)間間隔,是核自旋繞有效磁場(chǎng)進(jìn)行拉莫進(jìn)動(dòng)的周期,反映核自旋對(duì)于NV色心電子自旋相干性的調(diào)制[30];T2為各個(gè)峰的包絡(luò)曲線衰減到1/e的時(shí)間,反映系統(tǒng)退相干的快慢.NV色心電子自旋的相干性隨時(shí)間演化可近似為

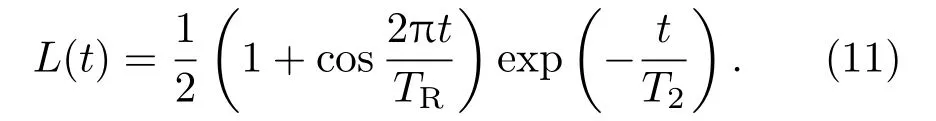
通過(guò)數(shù)據(jù)擬合,得到TW,TR與外磁場(chǎng)B的關(guān)系為

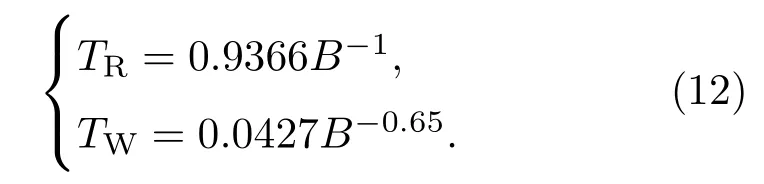
由圖4可知,橫向弛豫時(shí)間T2隨磁場(chǎng)增大整體上呈現(xiàn)增大趨勢(shì),并在B≥ 10 Gs(1 Gs=10?4T)時(shí)趨于一個(gè)定值[16],不適合用于指示磁場(chǎng)大小.TW和TR均隨磁場(chǎng)增大而減小,其中TW在1—100 Gs的磁場(chǎng)范圍內(nèi)與B?0.65成正比,在小磁場(chǎng)極限下趨向于定值;在可測(cè)量范圍內(nèi)TR∝1/(γnB)[23],對(duì)磁場(chǎng)變化響應(yīng)度較高.若通過(guò)TR與B的非線性關(guān)系間接確定磁場(chǎng)大小,可得到較高的精確度.由于曲線的斜率為即磁場(chǎng)越小,TR對(duì)磁場(chǎng)大小的響應(yīng)度越高.

圖4也反映了利用TR測(cè)量靜態(tài)弱磁場(chǎng)的磁場(chǎng)下限.當(dāng)外磁場(chǎng)較小時(shí),TR趨近于T2,實(shí)際測(cè)量過(guò)程中可能在第二個(gè)振蕩出現(xiàn)之前系統(tǒng)已經(jīng)完全退相干,此時(shí)只有第一個(gè)半峰,無(wú)法得到兩峰間距TR,可通過(guò)外加一個(gè)已知大小和方向的靜磁場(chǎng),使總磁場(chǎng)大小在可測(cè)量范圍內(nèi).

圖3 (網(wǎng)刊彩色)NV色心電子自旋退相干過(guò)程模擬 (a)NV色心|0〉態(tài)和|1〉態(tài)的相干性與相干時(shí)間T和外磁場(chǎng)大小B的關(guān)系;(b)B=10 Gs時(shí)NV色心的相干性隨相干時(shí)間的變化(插圖為前三個(gè)峰的放大)Fig.3.(color online)Numerical simulation of the NV center electron spin decoherence:(a)Coherence between|0〉and|1〉states as a function of total evolution time and magnetic field;(b)coherence as a function of evolution time under 10 Gs magnetic field.The inset shows the magni fication of the first three peaks.

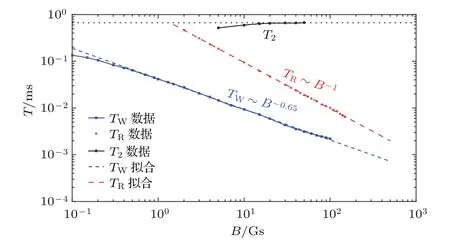
圖4 (網(wǎng)刊彩色)13C自然豐度環(huán)境下NV色心電子自旋退相干的TW,TR,T2與外磁場(chǎng)大小的關(guān)系Fig.4.(color online)The magnetic- field dependence of three different timescales,TW,TRand T2,for NV center electron spin coherence in a13C bath with natural abundance.

3.2 確定磁場(chǎng)大小

已知TR與B的關(guān)系,可以通過(guò)實(shí)驗(yàn)測(cè)得TR,從而間接確定NV主軸方向的磁場(chǎng)大小.為避免直接測(cè)量方向帶來(lái)的不確定性,可以使NV主軸分別處于三個(gè)相互正交的方向x,y,z上,測(cè)量TR并結(jié)合TR與B的非線性關(guān)系,確定每次主軸方向的磁場(chǎng)大小Bx,By,Bz,則待測(cè)磁場(chǎng)大小B可表示為

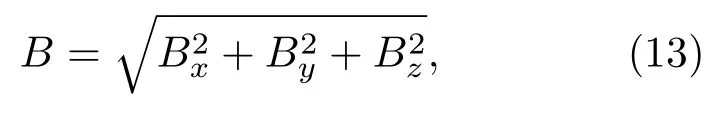
磁場(chǎng)大小即可確定.

3.3 確定磁場(chǎng)方向

由于x,y,z方向和各方向上磁場(chǎng)分量已知,磁場(chǎng)與x,y,z方向余弦分別為

由此可以確定磁場(chǎng)方向.每個(gè)磁場(chǎng)分量的方向有2個(gè)可能的取向,因此磁場(chǎng)方向有6個(gè)可能取向.為了確定磁場(chǎng)方向,可以先利用光學(xué)磁共振技術(shù)[31]觀察NV色心在外磁場(chǎng)下發(fā)生塞曼分裂的情況.

存在外磁場(chǎng)B時(shí),忽略高階小項(xiàng),哈密頓量中與磁場(chǎng)B有關(guān)的部分為

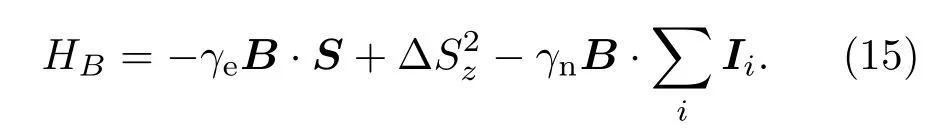
不考慮由13C和14N核自旋引起的超精細(xì)結(jié)構(gòu),則有

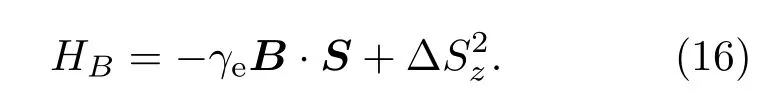
在Sz表象下,Sx,Sy,Sz的矩陣元分別如下(因子?略去未記):

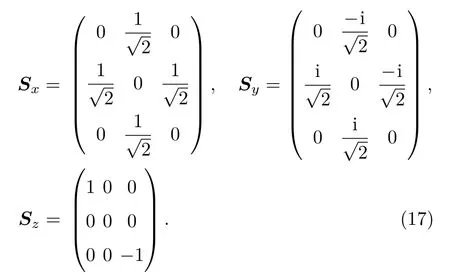
由定態(tài)薛定諤方程解能量本征值E得方程

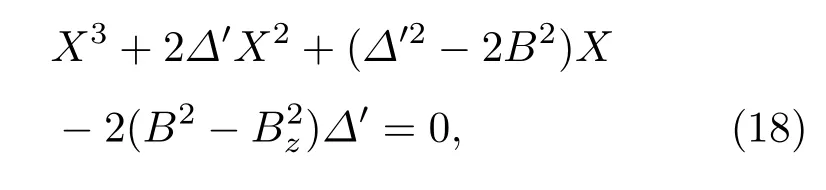
其中

若外界磁場(chǎng)B方向沿NV主軸方向,即B=Bz,則(18)式方程的解為

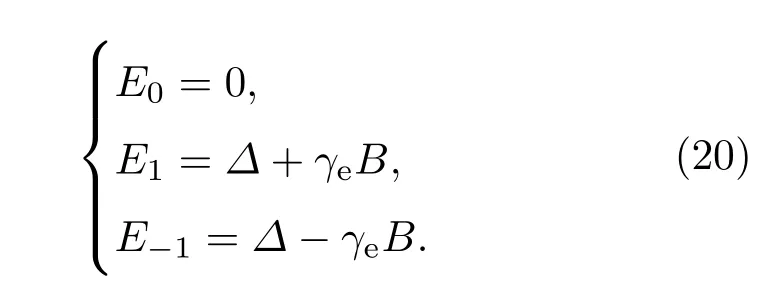
此時(shí)從|0〉態(tài)向|1〉態(tài)與|?1〉態(tài)躍遷的吸收或放出的光子頻率分別為Δ±γeB.當(dāng)NV主軸與外磁場(chǎng)方向相同時(shí),對(duì)該NV色心掃描光磁共振譜,理論結(jié)果如下:1)兩個(gè)共振峰關(guān)于Δ=2.87 GHz對(duì)稱;2)兩共振峰之間的頻率差δ=2γeB.由此可以確定外磁場(chǎng)方向.

3.4 測(cè)量靈敏度

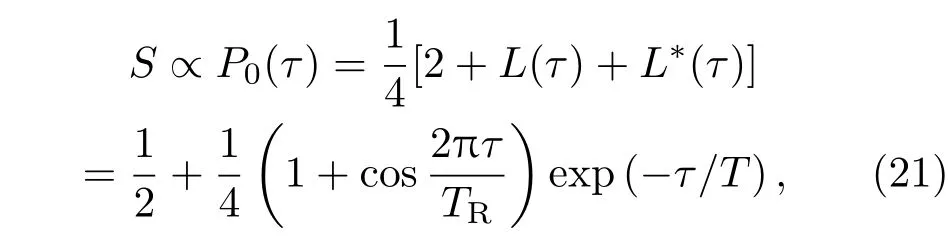
式中P0(τ)為系統(tǒng)末態(tài)中|0〉的布居數(shù).

由圖4可知,TR,T2的值均與外磁場(chǎng)大小B有關(guān).T2對(duì)B變化的響應(yīng)度遠(yuǎn)小于TR,因此,外磁場(chǎng)大小B變化一個(gè)小量δB時(shí),可將T2視為一個(gè)常數(shù),則由外磁場(chǎng)變化引起的熒光信號(hào)變化為

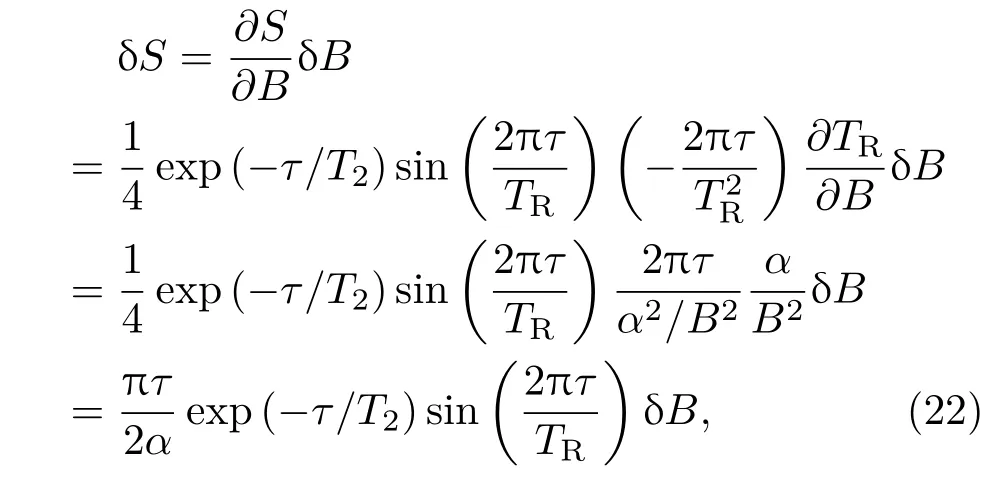
式中τ為積分時(shí)間,TR=αB?1((12)式),α=0.9366 ms·Gs.

同時(shí),由于熒光讀出時(shí)光子散射噪聲引起的讀出噪聲為

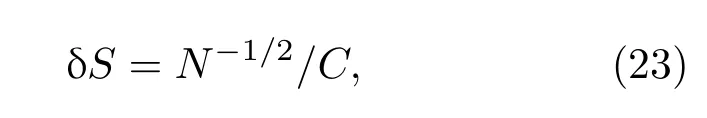
式中C為一個(gè)與收集效率有關(guān)的常數(shù),收集效率為5%時(shí),C≈0.3[32];N=T/τ為測(cè)量次數(shù),T為總的測(cè)量間隔.可測(cè)量的最小磁場(chǎng)改變量為

由此定義靈敏度為[32]

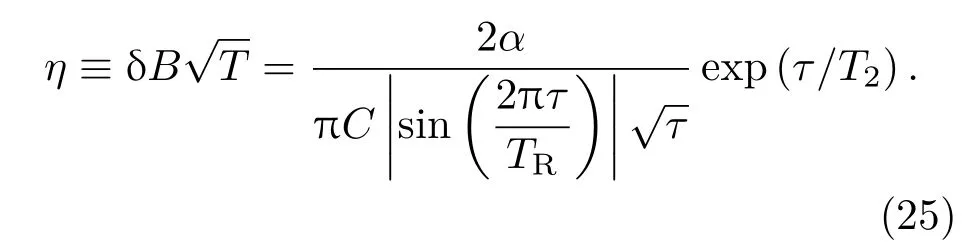
在采用的13C自然豐度的單個(gè)NV系統(tǒng)中,退相干時(shí)間T2≈0.5 ms,此時(shí)η≈20μT·Hz?1/2.對(duì)于含n個(gè)NV色心的集群樣品,由于熒光信號(hào)被放大n倍,信噪比增大,可使靈敏度提高倍.同時(shí),由(22)式可知延長(zhǎng)退相干時(shí)間也可以提高靈敏度.在單個(gè)NV色心系統(tǒng)中,電子自旋與13C核自旋之間的相互作用是造成NV退相干的主要原因.如圖5所示,隨著13C濃度增大,核與核之間的磁偶極相互作用造成各核自旋拉莫進(jìn)動(dòng)的不同步,進(jìn)而導(dǎo)致電子自旋退相干更加劇烈,退相干時(shí)間T2縮短.因此采用合適的脈沖序列和經(jīng)12C純化的金剛石樣品延長(zhǎng)退相干時(shí)間[33],從而顯著提高測(cè)量弱磁場(chǎng)的靈敏度.目前對(duì)于13C自然豐度的樣品T2可達(dá)0.6 s[16],另外可以通過(guò)同位素純化,將13C濃度降低到1/10000以內(nèi)[33],此時(shí)η≈60 nT·Hz?1/2.

表1 幾種主要的磁力計(jì)及其靈敏度Table 1.Sensitivities of different magnetometers.

為了對(duì)比NV色心和其他磁力計(jì)測(cè)量微弱磁場(chǎng)的精度,表1列舉了幾種主要磁力計(jì)的靈敏度.超導(dǎo)量子干涉儀的靈敏度雖然高于本文測(cè)弱磁場(chǎng)方法,但需要低溫(4 K)工作條件,對(duì)室外勘測(cè)不利.本文方法靈敏度已足以進(jìn)行地磁場(chǎng)量級(jí)的弱磁場(chǎng)測(cè)量,且可通過(guò)施加脈沖優(yōu)化和同位素純化的方法進(jìn)一步提高測(cè)量靈敏度.

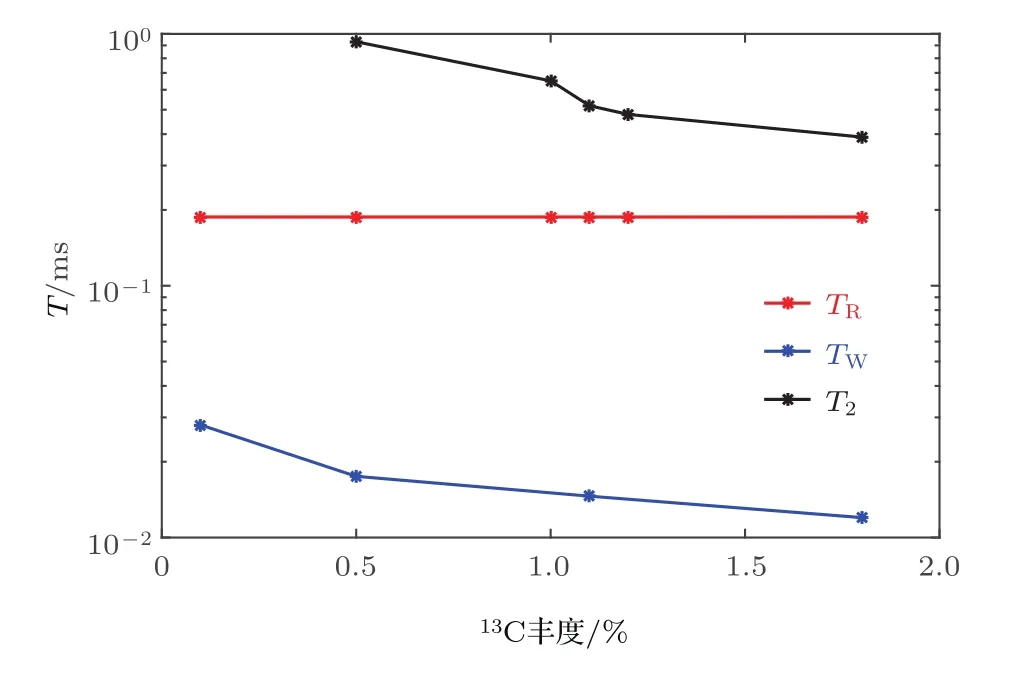
圖5 13C豐度對(duì)TW,TR,T2的影響(B=5 Gs)Fig.5.Effect of13C abundance on timescales TW,TR,T2(B=5 Gs).

4 結(jié) 論

地磁場(chǎng)強(qiáng)度約為0.5 Gs,屬于弱磁場(chǎng),在人類和動(dòng)物生活、科學(xué)研究等方面有重要應(yīng)用[34].本文借鑒鳥(niǎo)類感磁機(jī)理,提出了一種利用量子相干系統(tǒng)精確測(cè)量靜態(tài)弱磁場(chǎng)的方法.通過(guò)哈密頓量求解,簡(jiǎn)要分析了金剛石中NV色心電子自旋退相干的原因,模擬了高純度金剛石中單個(gè)NV色心與周?chē)?3C核自旋熱庫(kù)的耦合,得到了電子自旋|0〉態(tài)與|1〉態(tài)的相干性隨演化時(shí)間和外部磁場(chǎng)大小的分布,進(jìn)而得到退相干特征時(shí)間TW,TR,T2與外部磁場(chǎng)大小B的冪函數(shù)形式的高精確度關(guān)系.分別分析TW,TR,T2對(duì)外磁場(chǎng)B的響應(yīng)度,確定將TR作為本文方法中指示外磁場(chǎng)的“標(biāo)尺”,即對(duì)于一個(gè)特定的NV色心系統(tǒng),電子自旋退相干過(guò)程的TR與外磁場(chǎng)B有嚴(yán)格的對(duì)應(yīng)關(guān)系.只要在光學(xué)磁共振實(shí)驗(yàn)中確定TR,由TR-B曲線即可得到該環(huán)境下NV主軸方向的靜磁場(chǎng)分量,通過(guò)在相互正交方向上的三次測(cè)量,即可確定外磁場(chǎng)的三維分布.對(duì)于該方法造成的磁場(chǎng)方向的不確定性,可利用連續(xù)的光磁共振譜實(shí)驗(yàn)解決.NV色心主軸方向與外磁場(chǎng)方向平行時(shí),塞曼分裂的連續(xù)光磁共振譜將關(guān)于Δ=2.87 GHz對(duì)稱,通過(guò)調(diào)整NV色心指向,可大致確定磁場(chǎng)方向,由此消除該方法測(cè)量磁場(chǎng)方向的不確定性.本文方法對(duì)靜態(tài)弱磁場(chǎng)的測(cè)量靈敏度可達(dá)60 nT·Hz?1/2,且可通過(guò)增大樣品中NV色心濃度和同位素純化的方法達(dá)到更高的靈敏度.

[1]Kirtley J R 2010Rep.Prog.Phys.73 126501

[2]Lenz J,Edelstein S 2006IEEE Sens.J.6 631

[3]Oukhanski N,Stolz R,Zakosarenko V,Meyer H G 2002Physica C368 166

[4]Zhang X C,Zhao G P,Xia J 2013Acta Phys.Sin.62 218702(in Chinese)[張溪超,趙國(guó)平,夏靜2013物理學(xué)報(bào)62 218702]

[5]Phillips J B,Deutschlander M E,Freake M J,Borland S C 2001J.Exp.Biol.204 2543

[6]Liang C H,Chuang C L,Jiang J A,Yang E C 2016Sci.Rep.6 23657

[7]Cai C Y,Ai Q,Quan H T,Sun C P 2012Phys.Rev.A85 022315

[8]Rodgers C T,Hore P J 2009Proc.Natl.Acad.Sci.USA106 353

[9]Kominis I K 2009Phys.Rev.E80 056115

[10]Cai J M,Guerreschi G G,Briegel H J 2010Phys.Rev.Lett.104 220502

[11]Yang L P,Ai Q,Sun C P 2012Phys.Rev.A85 032707

[12]Doherty M W,Manson N B,Delaney P,Jelezko F,Wrachtrup J,Hollenberg L C L 2013Phys.Rep.528 1

[13]Dobrovitski V V,Fuchs G D,Falk A L,Santori C,Awschalom D D 2013Annu.Rev.Condens.Matter Phys.4 23

[14]Neumann P,Beck J,Steiner M,et al.2010Science329 542

[15]Liu G Q,Xing J,Ma W L,Li C H,Wang P,Po H C,Liu R B,Pan X Y 2017Phys.Rev.Lett.118 150504

[16]Bar-GillN,Pham L M,JarmolaA,BudkerD,Walsworth R L 2013Nat.Commun.4 1743

[17]Tao M J,Hua M,Ai Q,Deng F G 2015Phys.Rev.A91 062325

[18]Ladd T D,Jelezko F,La flamme R,Nakamura Y,Monroe C,O’Brien J L 2010Nature464 45

[19]Zhao N,Honert J,Schmid B,Klas M,Isoya J,Markham M,TwitchenD,JelezkoF,LiuRB,FedderH,Wrachtrup J 2012Nat.Nanotech.7 657

[20]Maze J R,Stanwix P L,Hodges J S,Hong S,Taylor J M,Cappellaro P,Jiang L,Gurudev-Dutt M V,Togan E,Zibrov A S,Yacoby A,Walsworth R L,Lukin M D 2008Nature455 644

[21]Balasubramanian G,Chan I Y,Kolesov R,Al-Hmoud M,Tisler J,Shin C,Kim C,Wojcik A,Hemmer P R,Krueger A,Hanke T,Leitenstorfer A,Bratschitsch R,Jelezko F,Wrachtrup J 2008Nature455 648

[22]Shi F,Zhang Q,Wang P F,Sun H B,Wang J R,Rong X,Chen M,Ju C Y,Reinhard F,Chen H W,Wrachtrup J,Wang J F,Du J F 2015Science347 1135

[23]Zhao N,Ho S W,Liu R B 2012Phys.Rev.B85 115303

[24]Liu D Q,Chang Y C,Liu G Q,Pan X Y 2013Acta Phys.Sin.62 164208(in Chinese)[劉東奇,常彥春,劉剛欽,潘新宇2013物理學(xué)報(bào)62 164208]

[25]Huang P,Kong X,Zhao N,Shi F Z,Wang P F,Rong X,Liu R B,Du J F 2011Nat.Commun.2 570

[26]Gruber A,Drabenstedt A,Tietz C,Fleury L,Wrachtrup J,von Borczyskowski C 1997Science276 2012

[27]Childress L,Taylor J M,S?rensen A S,Lukin M D 2006Phys.Rev.Lett.96 070504

[28]Song X K,Ai Q,Qiu J,Deng F G 2016Phys.Rev.A93 052324

[29]Yang W,Liu R B 2009Phys.Rev.B79 115320

[30]Stanwix P L,Pham L M,Maze J R,Le Sage D,Yeung T K,Cappellaro P,Hemmer P R,Yacoby A,Lukin M D,Walsworth R L 2010Phys.Rev.B82 201201

[31]Chen X D,Zou C L,Gong Z J,Dong C H,Guo G C,Sun F W 2015Light-Sci.Appl.41

[32]Taylor J M,Cappellaro P,Childress L,Jiang L,Budker D,Hemmer P R,Yacoby A,Walsworth R,Lukin M D 2008Nat.Phys.4 810

[33]Ishikawa T,Fu K M C,Santori C,Acosta V M,Beausoleil R G,Watanabe H,Shikata S,Itoh K M 2012Nano Lett.12 2083

[34]Zhao L,Yan T J 2013Acta Physica Sin.62 067702(in Chinese)[趙龍,顏廷君 2013物理學(xué)報(bào) 62 067702]

Measurement of weak static magnetic field with nitrogen-vacancy color center?

Li Lu-SiLi Hong-HuiZhou Li-LiYang Zhi-Sheng Ai Qing?

(Department of Physics,Beijing Normal University,Beijing 100875,China)

28 May 2017;revised manuscript

12 August 2017)

The accurate measurement of the weak geomagnetic field is of significance for different disciplines.It can provide sufficient navigation information for both human beings and different natural animal species.Inspired by avian magnetoreception models,we consider the feasibility of utilizing quantum coherence phenomena to measure weak static magnetic fields.We propose an experimentally feasible scheme to measure weak static magnetic fields with nitrogenvacancy color center in diamond.Nitrogen-vacancy color centers are regarded as an ideal platform to study quantum science as a result of its long coherence time up to a millisecond timescale at room temperature.In a high-purity diamond,the hyper fine interaction with the surrounding13C nuclear spins dominates the decoherence process.In this paper,by the cluster-correlation expansion,we numerically simulate the decoherence process between|0〉and|+1〉states of the individual nitrogen-vacancy color center electron spin in the13C nuclear-spin baths with various magnitudes of external magnetic fields.By applying the Hahn echo pulse sequence to the system,we obtain the coherence of the nitrogenvacancy color center electron spin as a function of total evolution time and magnetic field.Furthermore,we obtain the high-accuracy relationship between the three decoherence-characteristic timescales,i.e.,TW,TR,T2,and magnetic fieldB.Finally,we draw a conclusion thatTRhas the highest sensitivity to the magnetic field in the three timescales.Thus,for a certain nitrogen-vacancy color center,TRcan be the scale for the magnitude of the magnetic field,or rather,the component along the nitrogen-vacancy electronic spin axis.When measuring an unknown magnetic field,we adjust the nitrogen-vacancy axis to the three mutually orthogonal directions respectively.By this means,we obtain the three components of the magnetic field and thus the magnitude and direction of the actual magnetic field.The accuracy can reach as high as 60 nT·Hz?1/2,and can be further improved by using an ensemble of nitrogen-vacancy color centers or diamond crystals purified with12C atoms.In summary,our scheme may provide an alternative method of accurately measuring the weak geomagnetic field by the nitrogen-vacancy color center under ambient condition.

weak magnetic field detection,nitrogen-vacancy color center in diamond,decoherence

PACS:06.20.–f,03.67.–a,07.55.Ge,85.75.SsDOI:10.7498/aps.66.230601

*Project supported by the Undergraduate Research Foundation of Beijing Normal University,China,the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.11505007),and the Open Research Fund of the State Key Laboratory of Low-Dimensional Quantum Physics,Tsinghua University,China(Grant No.KF201502).

?Corresponding author.E-mail:aiqing@bnu.edu.cn

(2017年5月28日收到;2017年8月12日收到修改稿)

基于金剛石氮-空位色心對(duì)精確測(cè)量微弱靜磁場(chǎng)進(jìn)行了探索.金剛石氮-空位色心電子自旋的退相干時(shí)間高度依賴于外磁場(chǎng),而不同的退相干特征時(shí)間對(duì)磁場(chǎng)的靈敏度不同.對(duì)金剛石氮-空位色心電子自旋在不同強(qiáng)度外磁場(chǎng)下的退相干過(guò)程進(jìn)行模擬,得到不同退相干特征時(shí)間與磁場(chǎng)大小的高準(zhǔn)確度關(guān)系,提出了基于響應(yīng)度最高的退相干特征時(shí)間測(cè)量靜態(tài)弱磁場(chǎng)大小和方向的方法,并分析了該方法測(cè)量靜態(tài)弱磁場(chǎng)的靈敏度,證明該方法的測(cè)量靈敏度比一般磁場(chǎng)測(cè)量?jī)x器更高.

10.7498/aps.66.230601?北京師范大學(xué)本科生科研訓(xùn)練與創(chuàng)新創(chuàng)業(yè)項(xiàng)目、國(guó)家自然科學(xué)基金青年科學(xué)基金(批準(zhǔn)號(hào):11505007)、清華大學(xué)低維量子物理國(guó)家重點(diǎn)實(shí)驗(yàn)室開(kāi)放研究基金(批準(zhǔn)號(hào):KF201502)資助的課題.

?通信作者.E-mail:aiqing@bnu.edu.cn