人致荷載研究綜述

陳 雋

(1.同濟大學 土木工程學院，上海 200092; 2. 同濟大學 土木工程防災國家重點實驗室，上海 200092)

人致荷載研究綜述

陳 雋1,2

(1.同濟大學 土木工程學院，上海 200092; 2. 同濟大學 土木工程防災國家重點實驗室，上海 200092)

人致荷載是指建筑物的使用者在完成步行、跳躍、奔跑、舞蹈、屈伸、突然起立/坐下、上下樓梯等動作時施加于支撐結構上的動力作用，可引起建筑樓蓋、人行橋、長懸臂結構、體育看臺、柔性樓梯等大跨輕柔工程結構的振動，嚴重時可導致結構的振動舒適度問題。人致荷載是人致結構振動問題工程設計與舒適度評估的重要基礎。在總結人致荷載特點及其分類的基礎上，以步行、跳躍荷載為主，介紹了人致荷載研究的現狀和主要進展，分析了目前研究面臨的試驗和建模的挑戰，并初步探討了今后需要解決的一些問題。

人致荷載；振動舒適度；大跨結構；綜述

建筑結構中的使用者在完成步行、跳躍、奔跑、舞蹈、屈伸、突然起立、踏步以及上下樓梯等動作時對支撐結構所施加的動力作用稱為人致動力荷載，簡稱人致荷載，由其引起的建筑樓蓋、人行橋、長懸臂結構、柔性樓梯、體育看臺等大跨柔性工程結構的振動稱為人致結構振動。若結構振幅超過一定限值，則暴露于振動環境中的人員可出現注意力下降、頭暈、心慌等生理或心理上的不舒適感覺，稱為振動舒適度問題。此外，對于擁有振動敏感設備的醫院、廠房和實驗室等民用或工業建筑，人致結構振動還可能造成儀器定位精度下降、廢品率增加甚至機械轉子破壞等問題，可以和振動舒適度問題一起合并稱為人致工程結構振動的適用性問題。

人致工程結構振動問題由來已久，部隊齊步行軍過橋造成橋梁破壞的事例最廣為人知[1]。近年來更是隨著日本T橋[2]、英國千禧橋[3]、韓國TechnoMart大樓[4]等事件，以及世界范圍內大跨樓蓋、懸挑結構等輕柔結構的大量興建而受到研究者和工程界的高度關注[5-7]。相關研究工作沿著人致荷載的試驗/理論建模、人致結構振動分析方法和振動舒適度評價標準三個方向展開，分別涵蓋此問題的振源、傳播途徑和振動接收者三要素。這其中，評價標準的研究側重于振動對“人”的主觀感受影響的客觀定量，涉及人體工程學、生物醫學甚至心理學等領域，需要通過多學科交叉來完成。因此，有關振動舒適度評價標準的研究自成體系。結構振動分析方法用于計算人致荷載作用下的結構振動幅度，研究重點是提出面向工程設計的簡化方法，目前的難點是人群荷載作用下的人-結相互作用問題，響應計算結果的準確性仍然主要取決于人致荷載模型的合理性。因此，本綜述重點討論人致荷載研究的現狀和發展趨勢。

1 人致荷載的分類與特點

1.1 人致荷載的分類

人致荷載的研究主要面向單人荷載和人群荷載兩種情形，前者是后者的基礎。根據人的雙足在運動時是否始終與地面或支撐面有接觸，可把單人荷載分為連續型和非連續型兩類。它們的表達形式以及施加方式不同，前者包括步行、屈伸、突然起立/起立、踏步等，后者包括跳躍、跑動、舞蹈等。其中，屈伸(英文稱bounce或bob)是指雙足不離開地面的身體重心的上下運動，常見于體育比賽或演唱會中觀眾的歡慶動作。根據荷載的動力特性，人致荷載也可分為周期性和瞬時性。結構分析時，前者一般考慮其穩態反應，后者則需考慮瞬態反應。此外，根據是否有音樂、口令等外部引導因素，人致荷載也可分為一般性荷載和有節奏荷載兩類，各自對應的典型情況為建筑樓蓋(人行橋)上行人的步行以及體育場館中人群的集體跳躍。對于節奏性荷載類型，結構振動設計中往往需要考慮人群的協同性影響。

一般把人致荷載的峰值與人體靜體重的比定義為峰值因子kp，常見人致荷載的kp從小到大一般為步行、屈伸、跑動、跳躍等。表1總結了常見人致荷載的類型和特點。

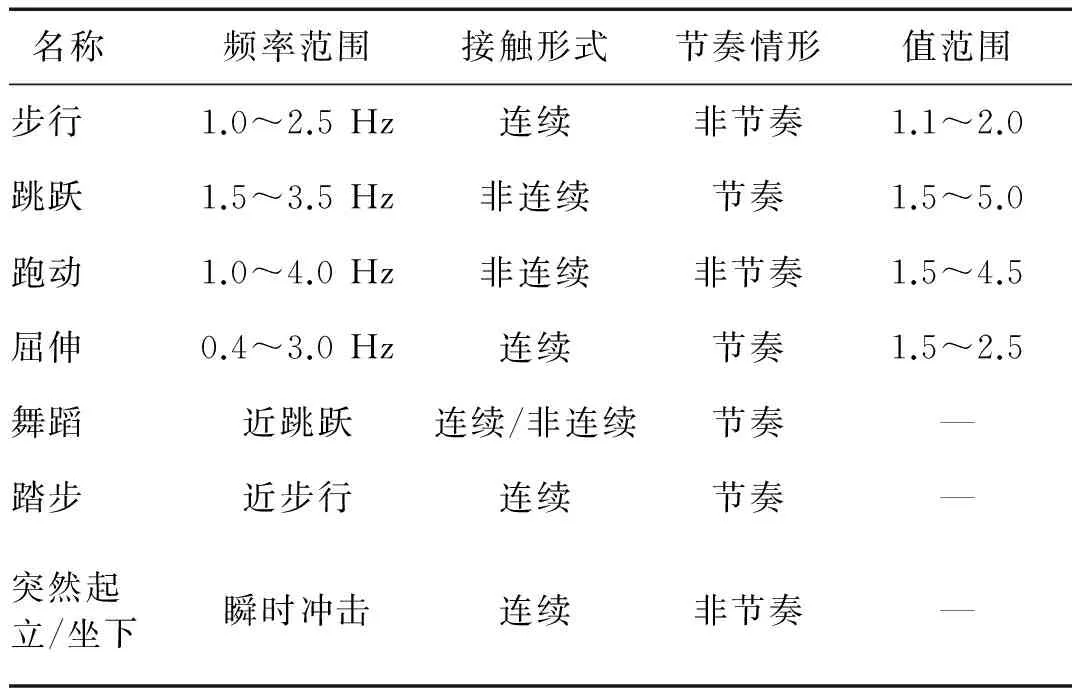
表1 常見人致荷載類型與特點Tab.1 Classification of human-induced loads

1.2 步行與跳躍荷載的特點與區別

顯然，無論哪種分類方法，步行和跳躍都是人致結構振動問題中最重要的兩種荷載形式，它們之間還具有如下的一些區別：① 作用點位置不同。步行是空間移動的連續性接觸荷載，跳躍則是固定作用點的非連續性接觸荷載，因此結構數值分析中應采用不同的荷載模擬方法以反應步行的移動特征。② 作用方向不同。對于人行橋等長線性結構，步行可以引起結構的豎向和水平振動，且水平振動可能成為控制作用，應重點考慮；跳躍荷載盡管也有水平分量[8]，但一般只考慮其引起的結構豎向振動；③ 作用性質不同。跳躍荷載具有沖擊荷載的特征，對于高頻樓板(>10 Hz)的影響大于步行荷載；④ 動力效應不同。跳躍荷載的峰值因子高于步行荷載，可引起更大幅度的結構振動；⑤ 頻率范圍不同。步行頻率指單位時間內的單步數，1.5 Hz即為1分鐘內走90步，步行荷載的頻率范圍大致在1.0～2.5 Hz；跳躍頻率指單位時間內的跳躍次數，其范圍大致在1.5～3.5 Hz。一般考慮步行荷載的4～5階倍頻、跳躍荷載的5～6階倍頻，則受影響結構頻率上限分別10 Hz和20 Hz左右。⑥ 人群作用的協同性不同。在體育館、公共建筑等工程結構中，跳躍荷載更容易出現人群協同作用的情況，并且有節奏群體跳躍時的協同因子要高于人群步行，因而可能造成更顯著的結構振動。

正是由于步行和跳躍荷載的重要性，各國學者都開展了大量的試驗研究和荷載建模工作，從研究的歷史進程和發展趨勢看，主要圍繞著試驗手段的進步和建模思路的創新兩條主線。

2 人致荷載的試驗研究

通過試驗獲得大量步行、跳躍荷載記錄并分析其動力特性與影響要素，是人致荷載建模的重要步驟和先決條件。試驗方案與試驗裝置的選擇決定了數據記錄的可靠性以及后續荷載模型的合理性。目前，試驗手段主要有直接測試方法及間接測試方法兩大類，前者利用測力板直接記錄人行走時足底與測力板間的接觸力，后者則通過結構振動響應、人體運動加速度等間接獲得行人荷載。

2.1 步行荷載試驗

如圖1所示，步行荷載(在生物力學領域中也稱地反力)包括豎向Fz、左右側向Fx以及前進方向Fy三個分量，一般認為Fz和Fx對結構振動舒適度分析有意義。

Harper[9]采用記錄單向地反力的測力板完成了土木工程領域內最早的步行荷載試驗，指出了步行荷載曲線呈“M”型，其雙峰特征和單足腳跟著地至腳尖離地的行走物理過程對應。此后，Galbraith等[10]、Matsumoto等[11]、Ohlsson等[12]、Ebrahimpour等[13-14], Kerr等[15-16]，Kasperski等[17]，Racic等[18]、陳雋等[19]以及其他很多研究者都曾利用測力板進行了步行荷載實測。測力板數量從單塊變為多塊、性能也從單向發展為三向測試。上述這些試驗具有大致相同的流程：測試者按照指定步頻模擬自然狀態下的行走并準確踏在測力板上，獲得步行荷載的單步時程曲線，它們只是在測試者數量、測試工況數等方面有差別。試驗結果的累積逐步揭示了步行荷載的曲線形狀及其成因、動載因子對頻率的依賴性以及步頻、步長、步速等步態參數的隨機性等特點。

此外，測力跑步機也是常用的試驗方法[20-26]，優勢在于不需要很大的試驗空間就可以記錄連續步行荷載，同時可以方便地調整步行速度。由于測試者行為受跑步機履帶控制，對于測力跑步機試驗數據的代表性還存有爭論。

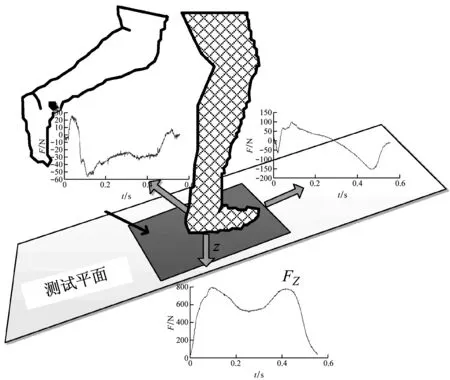
圖1 步行荷載的三個分量Fig.1 Three components of walking load

間接測試方法不采用測力板，通過對其他物理量的測試來反推步行荷載。一種方式是采用剛度很大的結構作為試驗裝置，測試其在人致荷載下的動力響應，再由已知的結構動力特性反演獲得結構上等效的步行荷載。Rainer等[27]采用這一思路，利用長17 m的兩跨連續桁架模型研究步行荷載。Sahnaci等[28]也采用類似的方法進行步行和跳躍荷載的研究。劉軍進等[29]利用剛性板及鋼梁下安裝力傳感器的方式記錄了行人單足落步、連續行走以及跳躍下的荷載曲線。這種間接法試驗不使用測力板，過程簡單并可得到連續步行荷載時程。但由于提取外部荷載時要濾除結構的慣性力部分，要求結構具有較高的基頻以錯開步行荷載的頻帶，因此對梁的跨度有限制，導致所得的實測步數有限，測試精度也有限。

另外一類間接測試方法是采用錄像(圖像)分析、三維動作捕捉、慣性傳感器甚至智能手機等技術獲得步行時人體的運動特征，并結合其他假定獲得步行荷載。例如Fujino、陳政清等分別通過錄像分析的方式得到了行人步頻的分布特性。張夢詩等[30]利用三維動作捕捉結合人體的單剛體力學模型計算獲得了步行荷載。Nimmen等[31]以及Bocian等[32]采用慣性傳感器記錄人體運動加速度，并結合已有的單人荷載數值模型[33]進行步行荷載的重構。Tan等[34]采用智能手機獲得步行者的運動加速度，再結合單剛體力學模型可計算得到步行荷載。

需要指出的是，盡管目前間接試驗技術的精度一般不高，并且可能是有限價值的結果(如僅能獲得步頻值)，但通過合理選擇試驗結構以及更合理的動力反演方法，利用間接測量方法實現人群荷載的同步測試是值得高度關注的手段。

2.2 跳躍荷載的試驗研究

與步行荷載試驗類似，跳躍荷載試驗也有直接測試和間接測試兩種方法。不同的是，由于跳躍的固定作用點特性，采用測力板即可獲得連續荷載記錄。Allen等[35]利用測力板研究人群有節奏運動(包括舞蹈和跳躍)時所產生的荷載作用，相關成果成為1985年版加拿大荷載規范的取值依據。Tuan等[36]采用0.6 m×0.4 m大小的測力平臺對22個測試者進行了單次跳躍、連續自由跳躍和非連續自由跳躍狀態的測試。Rainer等同樣利用測力板研究行走、跑動和跳躍時產生的作用力，研究發現實測最大跑動和跳躍荷載的峰值是當時規范推薦值的六倍，他們強調了合理的試驗方法和測試技術對獲得可靠結果的重要性。Pavic等采用測力板進行單人跳躍荷載試驗，結果表明由于人體重心在水平方向的加速度分量，豎向跳躍運動時也會產生水平分力。Parkhouse等[37]利用一塊裝有兩個測力板的地板(0.8 m×0.6 m)，測試了100人次共1 000條跳躍荷載的地反力時程，跳躍頻率有1.5 Hz，2.0 Hz、2.67 Hz和3.5 Hz四種。Agu等[38]采用相同的四種頻率并利用測力板進行了跳躍試驗。Yao等[39-40]設計了一個由懸臂鋼梁支撐的實驗平臺，可等效為單自由度體系并且可通過移動支撐的位置來調整其固有頻率。利用這一平臺Yao等研究了單人跳躍荷載以及人與結構的相互作用問題。實驗中，一體重為75 kg 的測試者在具有不同固有頻率的平臺結構上進行原地跳躍，跳躍力時程數據通過嵌于平臺內的測力板直接獲得，試驗主要進行了自由跳躍(約1.6 Hz)和按2.0 Hz頻率進行的原地跳躍。Racic等[41]在他們原有的剛性測力板的四周放置了安全平臺，用以保證試驗者在比較自然的狀態下進行跳躍試驗，獲得了55個人總共825個跳躍荷載實測數據，跳躍的頻率范圍增大到1.4 Hz～2.8 Hz，間隔為0.1 Hz。

對于間接試驗，Rainer采用17 m長兩跨連續桁架的間接測量方式進行跳躍荷載試驗，并反演跳躍荷載時程。Ebrahimpour等在研究人群跳躍的動力荷載時，用1.2 m×2.4 m大小的組合測力平臺對單次跳躍、連續周期跳躍和自由跳躍三種類型進行了測試，平臺采用4個應變計和9個位移傳感器(LVDTs)，并通過9自由度動力方程反算出人群跳躍荷載。Ji等[42]在提出跳躍荷載的傅里葉級數模型后，開展了間接試驗的驗證：單人在簡支梁中跨處隨著節拍器進行原地跳躍，記錄結構的動力響應，再根據單自由度結構動力方程，反演出跳躍荷載的力時程。Comer等[43]在研究看臺結構跳躍人群的同步性時，采用了看臺模擬裝置，由看臺響應推算出(等效)跳躍荷載力時程。Mazzoleni等[44]采用數字成像技術獲得測試者頭部、軀干和大腿三部分的加速度，結合人體動力學模型計算獲得跳躍荷載時程序。如前所述，間接測試方法精度相對直接法要低，但其在人群荷載的測試中具有優勢。

2.3 人群荷載的試驗研究

人致結構振動分析中實際需要考慮的是人群作用。然而由于試驗難度大，直接針對人群步行荷載動力特性的實驗研究非常有限，并且以間接試驗為主[45]。1996年，Ebrahimpour利用測力板測試過雙人、四人小組步行的合力，其中單人步行荷載由擬合試算的方式獲得。Comer等利用15塊測力板同時記錄小組人群跳躍荷載，是極少的人群荷載直接試驗研究。英國帝國理工學院利用倫敦千禧橋模型，測試了最多10人步行時所產生的總的水平向荷載，同樣無法給出單人的具體荷載[46]。Ji等[47]利用樓板響應的間接測試方法研究過64人跳躍時的荷載。

2.4 其他人致荷載試驗研究

相對于行走和跳躍，其他人致荷載類型出現的概率較低、場合也比較特殊。因此，相關試驗一般是伴隨步行或跳躍試驗開展。篇幅限制，這里僅對原地上下運動型荷載(Bounce)的研究做簡要總結。除去雙腳不離地的要求，Bounce和跳躍具有很高的相似性，上節所介紹的Tuan等的試驗中都另外開展了Bounce荷載的試驗。特別地，Comer等[48]設計制作了一個可容納15人的模擬體育看臺，其中每個座位下都有一個測力板，能夠同時采集15人的Bounce荷載時程。陳雋等[49]采用無線測力鞋墊測試了Bounce荷載特性。

3 人致荷載模型

合理的荷載模型與取值是進行結構設計與分析的前提，現有的人致荷載模型大體可分為確定性模型和隨機模型兩類。

3.1 確定性荷載模型

確定性荷載模型將行人的連續步行(或跳躍、bounce)視作一個周期性重復過程，假定每一步(跳)都完全相同。以步行荷載的豎向分量為例，可將其表示成式(1)的傅里葉級數形式，其他兩個方向上的表示形式相同。

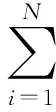
(1)

式中：G是人體靜體重，N為模型階數，av0為荷載時程的均值，連續步行時取為1.0，單步荷載時則小于1.0；是第i階傅里葉級數的系數，一般稱為動載因子DLF(Dynamic Load Factor),fp為步行頻率，φi是第i階相位角。

對于跳躍荷載，往往是給出每一次跳躍的荷載曲線(也稱為脈沖曲線)，一般采用半正弦(式(2))、半正弦平方(式(3a))或半余弦平方(式(3b))的形式，即

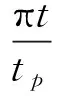
(2)

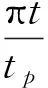
(3a)

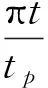
(3b)

式中：kp為峰值因子；tp是每次跳躍的觸地時間。

將式(2)或式(3)獲得單次跳躍曲線首尾相連，即可獲得連續跳躍荷載，也可將上兩式展開成式(1)的傅里葉級數形式，并得到對應各階的DLF值。基于上述三個式子，不同學者基于自己的試驗提出了不同的模型系數，具體見表2。

3.2 隨機荷載模型

確定性模型假定人致荷載為周期性重復過程，即每一步(跳)完全相同。事實上，以步行為例，同一步行者的每一步不可能完全相同，不同步行者在相同頻率下的步行荷載也不相同。Sim等[50]將以上兩種隨機性分別稱為“個體內變異性”(inter-subject variability)和“個體間變異性”(intra-subject variability)。Brownjohn等研究指出，由于人致結構振動計算一般采用共振假定，確定性周期模型的頻譜為Dirac函數，能量集中在共振頻率處，而實際能量在共振頻率附近有泄露，因此確定性模型可能會高估結構的動力響應，特別是高階共振的情況。他認為將步行荷載視作窄帶隨機過程更合理。遵循這樣一種思路，?ivanovic等[51]在傅里葉級數模型基礎上把步頻、步長、荷載幅值等視作符合正態分布的隨機變量，通過實驗數據統計分析給出了變量的概率分布規律以及主諧波和次諧波名義幅值的表達式，并假定各階相位角在[-π，π]之間均勻分布，建立了步行荷載隨機模型。

跳躍荷載隨機模型研究中，同樣有將確定性荷載模型中的控制參數處理為隨機變量的方式，并且主要針對單次跳躍的脈沖曲線(即一次跳躍的荷載時程曲線)。Racic等考慮脈沖形狀、單次跳躍持時、脈沖幅值三個隨機因素，采用多個高斯函數的疊加來擬合跳躍脈沖曲線形狀，通過變換高斯函數的數量可實現對三種基本脈沖曲線形狀的再現，文中最多用到100個高斯函數來反映曲線的局部特性，同時該隨機模型是基于實測數據庫。Sim等基于1 000條實測單人跳躍荷載曲線建立了一隨機荷載模型，考慮了脈沖曲線形狀、幅值和沖量大小，同時采用脈沖曲線形心與節拍器時刻的差來反映相位的變化。受試驗數據限制，文中只給出了三個頻率的計算參數。陳雋等[52]也提出了類似的隨機跳躍荷載模型，針對不同的跳躍頻率分別采用半正弦和半正弦平方作為脈沖荷載曲線，同時把接觸率和跳躍頻率作為兩個獨立隨機變量，并由試驗數據分析給出它們的概率分布特性。

功率譜模型(或相干函數模型)是描述隨機荷載更合理的方式，是否有公認的功率譜模型被認為是相關研究是否成熟的標志之一[53]。然而目前針對步行和跳躍荷載的功率譜模型研究還非常有限。Ohlsson等在其博士論文中指出了步行荷載頻域模型的重要性。Eriksson[54]根據幾個實測步行荷載樣本的功率譜曲線指出，譜線中每個峰值都有一定的譜線寬度，表明其是一個窄帶隨機過程，僅采用動載因子在時域上描述并不能準確地表達步行荷載的特性。Brownjohn利用測力跑步機獲得連續步行荷載記錄并研究了步行荷載的功率譜曲線，但未給出具體表達式。

3.3 荷載模型小結

表2、3、4分別總結了步行、跳躍和Bounce的部分已有荷載模型及其參數取值。圖2是表2所有步行荷載模型作用下，單位質量單自由度系統反應譜曲線的比較，跳躍和Bounce的反應譜曲線結果類似。從圖2可見，由于在模型階數、動載因子以及相位角等參數上的巨大差別，不同荷載模型所獲得的結構動力響應差別很大，可以導致完全不同的振動舒適度的評價結果。

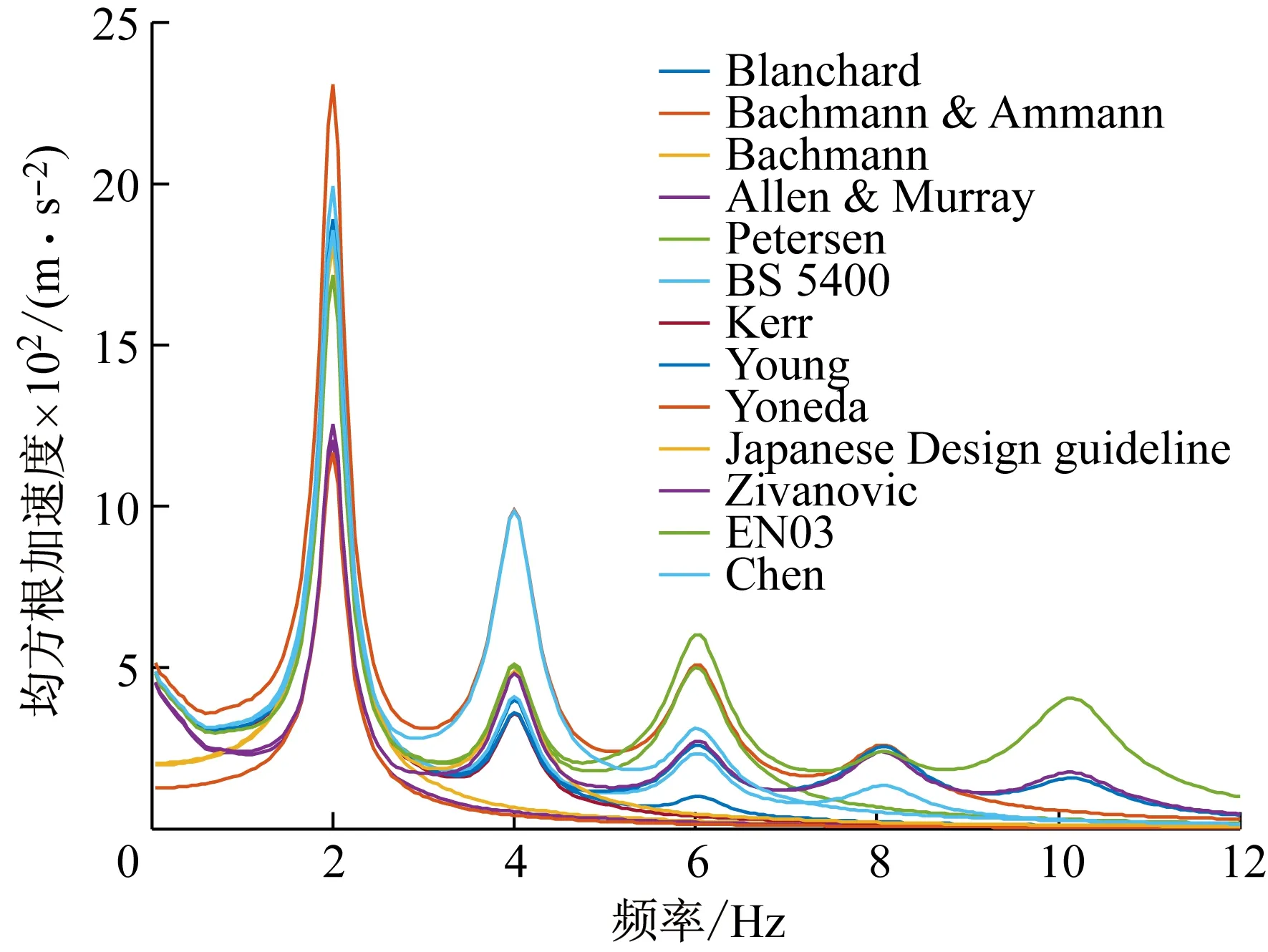
圖2 步行荷載模型單自由體系反應譜曲線比較

Fig.2 Comparison of response spectrum curves of SDOF system to different walking load models

表2 部分步行荷載模型及其動載因子(豎向)Tab.2 Avalialbe walking load models and their DLF values (vertical direction only)

表3 部分跳躍荷載模型及其參數取值Tab.3 Available jumping load models and their parameters

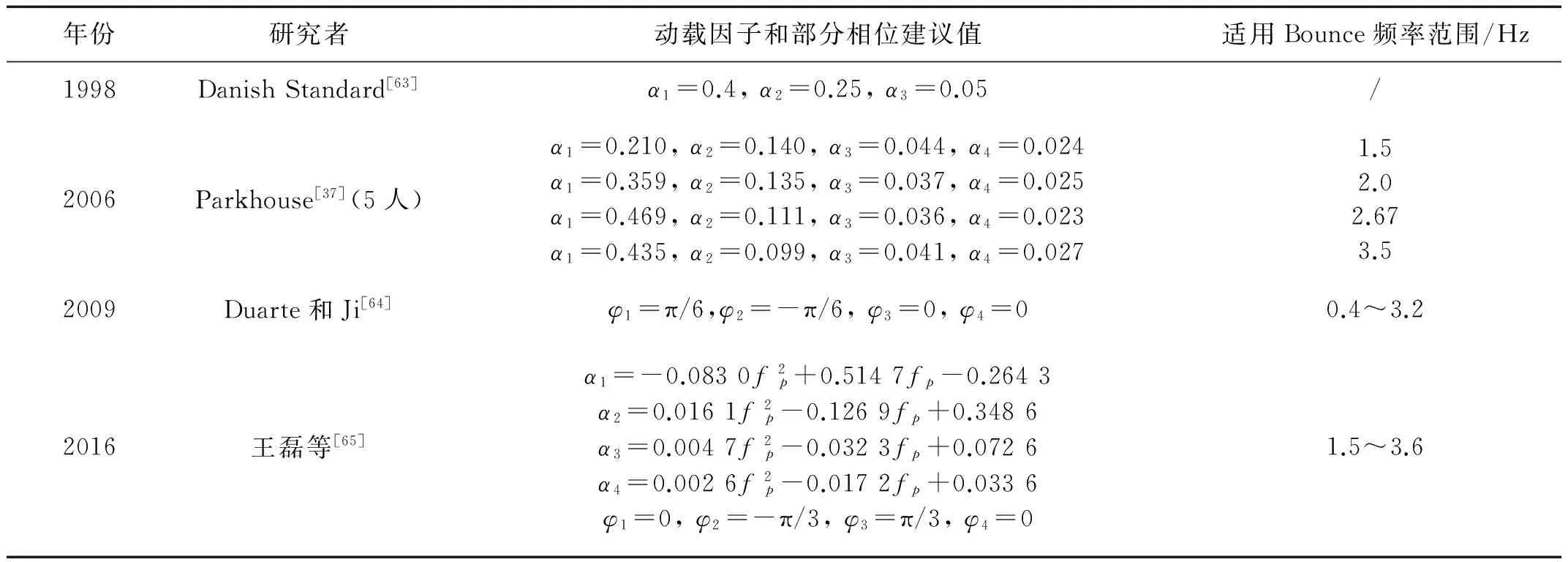
表4 部分Bounce荷載模型及其參數取值Tab.4 Available bounce models and theirs parameters

4 需進一步深入研究的問題

綜合以上關于人致荷載試驗與理論建模研究的現狀，結合面向人致結構振動分析的基本需求，可以從試驗和建模兩個方面梳理出人致荷載領域一些值得深入研究的問題。

4.1 荷載試驗技術的創新與突破

測力板從單向到三向、單塊到多塊; 從測力板到測力跑步機；從有線測試到無線測試乃至非接觸式測試，設計采用更合理的試驗裝置一直是人致荷載試驗研究發展的基本主線。針對土木工程領域的需求，通過傳感器技術、信號分析、虛擬現實乃至生物醫學等多學科領域交叉創新的途徑，有望迅速解決如下一些技術難題。

(1)新型單人荷載試驗技術的開發。單人荷載試驗技術要突破測試時間和空間的限制，同時應保證測試者在自然運動狀態下獲得連續的三向地反力時程。直接測試法中無線測力鞋墊是一種可行的方案，間接測試法可能的途徑很多，也最有可能出現突破。

(2)振動表面上單人荷載的試驗技術。現有的人致荷載試驗絕大多數在剛性、靜止地面上完成，在柔性及運動表面(即振動的結構表面)上行人的步態會發生變化，從而引起荷載的變化，并進一步改變結構的振動狀態，即會出現所謂的人與結構的相互作用問題。相應的試驗技術應能同步記錄行人步態特征、界面力以及結構響應三方面的信息。圖像分析、動作捕捉、高速攝影以及虛擬現實技術有望用來解決這一問題。

(3)小組/人群荷載試驗技術的創新。對于多人或人群試驗，除去突破測試時間和空間的限制外，還要進一步解決多人同步性測試和大測試樣本之間的矛盾。此時，高精度的單人試驗技術能否直接推廣到多人也存有挑戰。人群荷載試驗技術是目前國際范圍內的研究熱點，尚未出現公認合理有效的試驗技術。

(4)荷載試驗的標準化要求。不同于以往的任何荷載類型，人致荷載的試驗樣本極其特殊。不同學者的試驗，在測試樣本數量、參與者年齡段、體重分布、測試時間長度、測試工況順序(例如，是遞增完成不同頻率的工況，還是隨機完成)等試驗標準上差異顯著，試驗結果離散性大且難以合理解釋。人致荷載試驗方法的標準化是今后不同國家人致荷載規范對比和統一的基礎。

(5)人致荷載數據庫的建立。累積試驗數據并建立與地震、臺風類似的數據庫對于荷載的理論建模以及人致結構振動分析方法的研究具有支撐意義。標準化的試驗步驟使得研究者可以充分利用不同學科，如康復醫學、步態分析和運動醫學等，的試驗數據。

4.2 新一代人致荷載的分析模型

伴隨試驗技術的不斷突破以及試驗數據的不斷積累，如下一些人致荷載建模的問題有望得到更深入的探索和闡述。

(1)人致荷載物理模型的建立。目前基于現象學研究范式所獲得的荷載統計模型(見3.3小節)，初步解決了工程設計的急需，但不能把握“人致荷載源于人體運動”的這一物理機制。急需建立新一代基于物理機制的荷載模型，已有的嘗試包括單剛體、多剛體、倒擺、雙足行走模型等[66]。物理模型對于解釋人群作用下結構系統阻尼變化(例如負阻尼)、人與結構相互作用等現象，從而準確計算結構的動力響應至關重要。在物理模型中如何體現人的“智能”，即行人根據振動環境對自己的步態的調整、以及對自己行為的控制，是極具挑戰性的理論問題。

(2)人致荷載的功率譜模型的建立。有無公認的功率譜模型，往往是隨機荷載建模研究是否成熟的標志，以此為標準人致荷載的研究還遠未成熟。在確定性周期模型基礎上，從隨機過程的角度建立人致荷載的功率譜模型，對于人致結構振動可靠度分析以及振動的疲勞分析具有應用價值。

(3)人群荷載模型的建立。工程結構設計中急需的人群荷載模型目前仍處在研究階段，尚未有普遍認可的模型。其建模的核心是如何描述人群中個體間的協同性，即人群中單人間保持動作同步的程度。因此，在成熟的單人荷載模型基礎上，由實測數據獲得人群中不同個人之間協同性的相關性結構及其控制要素的分布特性是關鍵。

(4)面向工程結構設計的人致荷載的概率取值標準。表2、3、4中不同研究者提供的DLF系數，有的是試驗數據的均值，也有的是含有一定保證率的值，標準不一。為了與現有的荷載規范體系的可靠度基礎一致，應該對不同類型的人致荷載的回歸期、保證率等取值標準進行研究。

[1] WOLMUTH B, SURTEES J. Crowd-related failure of bridges[J]. Proceedings of the Institution of Civil Engineers-Civil Engineering, 2003, 156(3): 116-123.

[2] FUJINO Y, PACHECO B M, NAKAMURA S I, et al. Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge[J]. Earthquake Engineering & Structural Dynamics, 1993, 22(9): 741-758.

[3] DALLARD P, FITZPATRICK T, FLINT A, et al. London Millennium Bridge: pedestrian-induced lateral vibration[J]. Journal of Bridge Engineering, 2001, 6(6): 412-417.

[4] LEE S H, LEE K K, WOO S S, et al. Global vertical mode vibrations due to human group rhythmic movement in a 39 story building structure[J]. Engineering Structures, 2013, 57: 296-305.

[5] RACIC V, PAVIC A, BROWNJOHN J M W. Experimental identification and analytical modelling of human walking forces: Literature review[J]. Journal of Sound and Vibration, 2009, 326(1): 1-49.

[6] 陳政清, 華旭剛. 人行橋的振動與動力設計[M]. 北京：人民交通出版社, 2009.

[7] 李愛群, 陳鑫, 張志強, 大跨樓蓋結構減振設計與分析[J]. 建筑結構學報, 2010, 31(6): 160-170.

LI Aiqun, CHEN Xin, ZHANG Zhiqiang. Design and analysis on vibration control of long-span floor structures[J]. J. of Building Structures, 2010, 31(6): 160-170.

[8] PAVIC A, YU C H, BROWNJOHN J M W, et al. Verification of the existence of human-induced horizontal forces due to vertical jumping[J]. Proceedings of IMAC XX, 2002: 4-7.

[9] HARPER F C, WARLOW W J, CLARKE B L. The forces applied to the floor by the foot in walking[M]. HM Stationery Off, 1961.

[10] GALBRAITH F W, BARTON M V. Ground loading from footsteps[J]. The Journal of the Acoustical Society of America, 1970, 48(5): 1288-1292.

[11] MATSUMOTO Y, NISHIOKA T, SHIOJIRI H, et al. Dynamic design of footbridge[C]. IABSE proceedings, 1978: 17-18.

[12] OHLSSON S V, GSKOLA C T H. Floor vibrations and human discomfort[M]. Division of Steel and Timber Structures, 1982.

[13] EBRAHIMPOUR A, HAMAM A, SACK R L, et al. Measuring and modeling dynamic loads imposed by moving crowds[J]. Journal of Structural Engineering, 1996, 122(12): 1468-1474.

[14] EBRAHIMPOUR A, SACK R L. Modeling dynamic occupant loads[J]. Journal of Structural Engineering, 1989, 115(6): 1476-1496.

[15] KERR S C, BISHOP N W M. Human induced loading on flexible staircases[J]. Engineering Structures, 2001, 23(1): 37-45.

[16] KERR S C. Human induced loading on staircases[D]. University of London, 1998.

[17] SAHNACI C, KASPERSKI M. Random loads induced by walking[J]. Proceedings of the Sixth European Conference on Structural Dynamics, 2005(1): 441-446.

[18] RACIC V, BROWNJOHN J M W. Stochastic model of near-periodic vertical loads due to humans walking[J]. Advanced Engineering Informatics, 2011, 25(2): 259-275.

[19] 陳雋, 彭怡欣, 王玲. 基于步態分析技術的三向單足落步荷載曲線試驗建模[J]. 土木工程學報, 2014，47(3): 79-87.

CHEN Jun, PENG Yixin, WANG Ling. Experimental investigation and mathematical modeling of single footfall load using motion capture technology[J]. China Civil Engineering Journal, 2014, 47(3): 79-87.

[20] WHITE S C, YACK H J, TUCKER C A, et al. Comparison of vertical ground reaction forces during overground and treadmill walking[J]. Medicine and Science in Sports and Exercise, 1998, 30(10): 1537-1542.

[21] BELLI A, BUI P, BERGER A, et al. A treadmill ergometer for three-dimensional ground reaction forces measurement during walking[J]. Journal of Biomechanics, 2001, 34(1): 105-112.

[22] BROWNJOHN J M W, PAVIC A, OMENZETTER P. A spectral density approach for modelling continuous vertical forces on pedestrian structures due to walking[J]. Canadian Journal of Civil Engineering, 2004, 31(1): 65-77.

[23] 袁旭斌, 孫利民, 人行橋人致振動特性研究[D]. 上海：同濟大學, 2006

[24] PAOLINI G, DELLA CROCE U, RILEY P O, et al. Testing of a tri-instrumented-treadmill unit for kinetic analysis of locomotion tasks in static and dynamic loading conditions[J]. Medical Engineering & Physics, 2007, 29(3): 404-411.

[25] RACIC V, BROWNJOHN J M W. Mathematical modelling of random narrow band lateral excitation of footbridges due to pedestrians walking[J]. Computers & Structures, 2012, 90: 116-130.

[26] 陳雋, 王浩祺, 彭怡欣. 行走激勵的傅里葉級數模型及其參數的實驗研究[J]. 振動與沖擊, 2014, 33(8): 11-15.

CHEN Jun, WANG Haoqi, PENG Yixin. Experimental investigation of Fourier-series model of walking load and its coefficients[J]. Journal of Vibration and Shock, 2014, 33(8): 11-15.

[27] RAINER J H, PERNICA G, ALLEN D E. Dynamic loading and response of footbridges[J]. Canadian Journal of Civil Engineering, 1988, 15(1): 66-71.

[28] SAHNACI C, KASPERSKI M. A load model for running, in 7th Eruopean Conference on Structural Dynamics EURODYN2008[C]. 2008: 7-9 July, Southampton, p. E260.

[29] 劉軍進, 肖從真, 潘寵平. 跳躍和行走激勵下的樓蓋豎向振動反應分析[J]. 建筑結構, 2008, 38(11):108-110.

LIU Junjin, XIAO Congzhen, PAN Chongping. Investigation on response of floor vibration under jumping and walking excitation[J]. Building Structure, 2008, 38(11): 108-110.

[30] 張夢詩, 陳雋, 彭怡欣, 等, 基于動作捕捉與剛體動力學的步行荷載重構與仿真[J]. 應用基礎與工程科學學報, 2013，21(5): 961-972.

ZHANG Mengshi, CHEN Jun, PENG Yixin, et al. Reproduction and simulation of walking induced load via motion capture technique and inverse dynamics of rigid body models[J]. Journal of Basic Science and Engineering, 2013, 21(5): 961-972.

[31] VAN Nimmen K, LOMBAERT G, JONKERS I, et al. Characterisation of walking loads by 3D inertial motion tracking[J]. Journal of Sound and Vibration, 2014, 333(20): 5212-5226.

[32] BOCIAN M, BROWNJOHN J M W, RACIC V, et al. A framework for experimental determination of localised vertical pedestrian forces on full-scale structures using wireless attitude and heading reference systems[J]. Journal of Sound and Vibration, 2016, 376: 217-243.

[33] LI Q, FAN J S, NIE J G, et al. Crowd-induced random vibration of footbridge and vibration control[J]. Journal of Sound and Vibratoin, 2010, 329: 4068-4092.

[34] TAN H, CHEN J, PAN Z Y. Experimental verification of mobile phones for vibration measurements[C]//In the 7thConference on Structural Health Monitoring of Intelligent Infrastructure, 2015: July 1-3, Torino, Italy.

[35] ALLEN D E, RAINER J H, PERNICA G. Vibration criteria for assembly occupancies[J]. Canadian Journal of Civil Engineering, 1985, 12(3): 617-623.

[36] TUAN C Y, SAUL W E. Loads due to spectator movements[J]. Journal of Structural Engineering, 1985, 111(2): 418-434.

[37] PARKHOUSE J G, EWINS D J. Crowd-induced rhythmic loading[J]. Proceedings of the Institution of Civil Engineers: Structures and Buildings, 2006, 159(5): 247-259.

[38] AGU E, KASPERSKI M. A statistical approach to loads induced by bobbing[C]. Structural Dynamics EURODYN, 2008.

[39] YAO S, WRIGHT J R, PAVIC A, et al. Experimental study of human-induced dynamic forces due to jumping on a perceptibly moving structure[J]. Journal of Sound and Vibration, 2006, 296(1): 150-165.

[40] YAO S, WRIGHT J R, PAVIC A, et al. Forces generated when bouncing or jumping on a flexible structure[C]. Proceedings of the International Conference on Noise and Vibration, 2002, 2: 563-572.

[41] RACIC V, PAVIC A. Stochastic approach to modelling of near-periodic jumping loads[J]. Mechanical systems and signal processing, 2010, 24(8): 3037-3059.

[42] JI T, ELLIS B R. Floor vibration induced by dance-type loads: theory[J]. Structural Engineer, 1994, 72: 37-37.

[43] COMER A, BLAKEBOROUGH A, WILLIAMS M S. Crowd coordination in jumping tests on a model grandstand[C]. 7th Eur. Conf. on Struct. Dyn, 2008.

[44] MAZZOLENI P, ZAPPA E. Vision-based estimation of vertical dynamic loading induced by jumping and bobbing crowds on civil structures[J]. Mechanical Systems and Signal Processing, 2012, 33: 1-12.

[45] JONES C A, REYNOLDS P, PAVIC A. Vibration serviceability of stadia structures subjected to dynamic crowd loads: a literature review[J]. Journal of Sound and Vibration, 2011, 330(8): 1531-1566.

[46] SETRA F. Assessment of vibrational behavior of footbridge under pedestrian loading[R]. Technical guide SETRA, Paris, France, 2006.

[47] ELLIS B R, JI T J. Loads generated by jumping crowds: Experimental Assessment[C]. Taylor & Francis Group, 2002.

[48] COMER A J, BLAKEBOROUGH A, WILLIAMS M S. Rhythmic crowd bobbing on a grandstand simulator[J]. Journal of Sound and Vibration, 2013, 332(2): 442-454.

[49] 陳雋, 王磊, 樓佳悅, 等. 單人Bounce荷載下樓蓋結構加速度反應譜設計[J]. 振動與沖擊, 2015, 34(5): 14-19.

CHEN Jun, WANG Lei, LOU Jiayue, et al. Acceleration response spectrum for predicting floor vibration due to single human bounce load[J]. Journal of Vibration and Shock, 2015, 34(5): 14-19.

[50] SIM J, BLAKEBOROUGH A, WILLIAMS M S, et al. Statistical model of crowd jumping loads[J]. Journal of Structural Engineering, 2008, 134(12): 1852-1861.

[52] 陳雋, 王玲, 陳博, 等, 跳躍荷載動力特性與荷載模型實驗研究[J]. 振動工程學報, 2014, 27(1): 16-24.

CHEN Jun, WANG Ling, CHEN Bo, et al. Dynamic properties of human jumping load and its modeling: experimental study[J]. Journal of Vibration Engineering, 2014, 27(1): 16-24.

[53] 李杰, 閆啟. 結構隨機動力激勵的物理模型: 以脈動風速為例[J]. 工程力學, 2009, 26(增刊1): 175-185.

LI Jie, YAN Qi. Physical models for the stochastic dynamic excitations of structures: in the case of fluctuating wind speed[J]. Engineering Mechancis, 2009, 26(Sup1): 175-185.

[54] ERIKSSON P E. Vibration of low-frequency floors-dynamic forces and response prediction[M]. Chalmers University of Technology, 1994.

[55] BLANCHARD J, DAVIES B L, SMITH J W. Design criteria and analysis for dynamic loading of footbridges[C]//Proceeding of a Symposium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory, Crowthorne, Berkshire, England, 1977: May 19.

[56] BACHMANN H, AMMANN W. Vibrations in structures: induced by man and machines[M]. Zurich, Switzerland: Int. Association for Bridge and Structural Engineering, 1987.

[57] ALLEN D E, MURRAY T M. Design criterion for vibrations due to walking[J]. Engineering Journal, 1993, 30(4): 117-129.

[58] PETERSEN C H. Dynamik der baukonstruktionen[M]. Vierweg, Braunschweig /Wiesbaden, Germany, 1996.

[59] INSTITUTION B S. Appendix C vibration serviceability requirements for foot and cycle track bridges[S]. BS 5400, Part 2, BSI, London, UK, 1999.

[60] YOUNG P. Improved floor vibration prediction methodologies[C]. ARUP Vibration Seminar, 2001, 4.

[61] AIJ Recommendations for Loads on Buildings, Chapter 4[S]. Japan, 2004.

[62] Design of Footbridge, Footbridge Guidelines EN03, Chapter 4.5 Step 5: Determination of maximum acceleration[S]. Germany, 2008.

[63] DS, Code of Practice for Loads for the Design of Structures[M]. Denmark, 1998.

[64] DUARTE E, JI T. Action of individual bouncing on structures[J]. Journal of Structural Engineering, 2009, 135(7): 818-827.

[65] 王磊, 陳雋, 樓佳悅, 等, 單人Bounce荷載的實驗建模研究[J]. 振動與沖擊, 2016, 35(17): 55-60.

WANG Lei, CHEN Jun, LOU Jiayue, et al. Modeling with tests for single human bounce load[J]. Journal of Vibration and Shock, 2016, 35(17): 56-60.

[66] QIN J W, LAW S S, YANG Q S, et al. Pedestrian-bridge dynamic interaction, including human participation[J]. Journal of Sound and Vibration, 2013, 332(4): 1107-1124.

Areviewofhuman-inducedloadsStudy

CHEN Jun1,2

(1. College of Civil Engineering, Tongji University, Shanghai, 200092, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai, 200092, China)

Human-induced loads are dynamic actions exerted on supporting parts of structures by their users due to users’ walking, jumping, running, dancing, bend and stretch, suddenly seating sown or standing up, and going up and down stairs to cause vibrations of long-span light and flexible engineering structures, such as, long-span floors, pedestrian bridges, long cantilevered structures, sports grandstands and flexible stairs; if those loads are serious, it may lead to vibration serviceability problems. Studying human-induced loads is an important foundation for structures’ engineering design and comfort evaluation due to human-induced vibrations. Here, based on summarizing the characteristics of human-induced loads and classifying them, the state-of-the-art studies and developments of human-induced loads were then reviewed, the loads due to human’s walking and jumping were focused on, challenges of advanced test techniques and modeling faced by researchers were analyzed, the problems to be solved in future were discussed preliminarily.

human-induced loads; vibration serviceability; long-span structures; literature review

國家自然科學基金(51478346)；土木工程防災國家重點實驗室(SLDRCE14-B-16)

2016-07-13 修改稿收到日期：2016-08-13

作 者 陳雋 男，博士，教授，博士生導師，1972年生

TU311

A

10.13465/j.cnki.jvs.2017.23.001