基于層次變權的物流網絡流量分配模型
周曉
福建江夏學院工商管理學院,福建 福州 350108
隨著經濟全球化的不斷深入,物流對社會經濟發展的推動作用日益凸顯。物流網絡是物流活動開展的載體,網絡靜態的結構布局和動態的貨流量分布都會對物流效率和效益產生影響。如何在靜態的物流網絡中動態地分配貨流量,以滿足生產、交換和消費的需要是一個值得思考的問題。
關于物流網絡的貨流量分配問題,尋找最短路徑進行貨流量分配是決策者常用的方法。針對最短路徑問題,已有大量的研究成果[1-9]。大多數學者以距離、時間、成本中某種單一屬性度量路徑的長度,進而研究最短路徑的求解算法。如文獻[6]以時間作為路徑的長度單位,在考慮線路容量約束的條件下,對隨機流網絡的最短路徑問題進行了研究。在實際情況中,我們對路徑的選擇不僅僅只關注時間或者距離的長短,還會考慮所耗費成本的多少等其他因素,因此,最短路徑的選擇應是多因素綜合權衡之后的結果。有學者從多屬性角度研究了最短路徑問題,如文獻[8]對物流運輸網絡多目標最短路問題進行了研究,在將多目標轉化為單目標時,對每個目標的權重分配充分考慮了決策者的偏好。然而,以往的研究方法忽略了路徑屬性的動態性,物流網絡中節點和線路的通過時間和通過成本等會隨著所流經貨物量的大小的不同而變化,因此對各因素屬性的權衡不應固定不變。
近年來,變權理論日益受到關注,針對變權理論及其應用的研究成果不斷出現[10-15]。變權理論的核心思想是:影響因素的權重隨著因素狀態值的變化而變化,使因素的權重能更好地體現相應因素在決策中的作用。物流網絡具有復雜性和動態性特征,因此,在進行物流網絡的路徑選擇及貨流量分配時,應從動態的角度考慮多種因素的綜合影響。本文在分析物流網絡構成要素及要素屬性之間相互關系的基礎上,對這些因素由底至頂進行分層,結合決策者的因素偏好,依據變權理論,研究各層因素權重的構成與計算方法,從而建立物流網絡層次變權模型,在此基礎上對物流網絡的貨流量分配優化問題進行研究。
1 物流網絡層次變權模型的構建
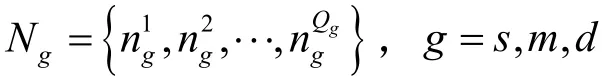
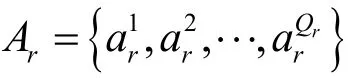
屬性層的屬性值往往以不同的物理單位進行度量,故屬性值之間不具可比性。利用式(1)對屬性值進行無量鋼化,使關聯屬性具有可比性,進而可進行權重分配。
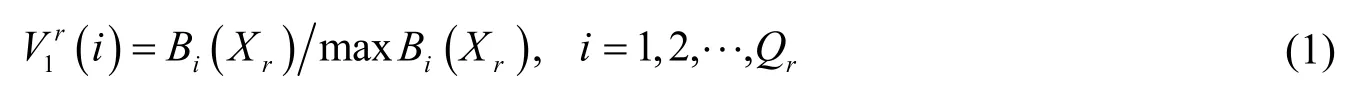
式中,Xr為r的貨流分配向量,Bi(Xr)為r的屬性i的屬性值向量,為r在屬性層(第1層)中屬性i的狀態值向量。并且,屬性層之上的每層因素的狀態值由其直接下層相關因素的狀態值和變權決定,即:
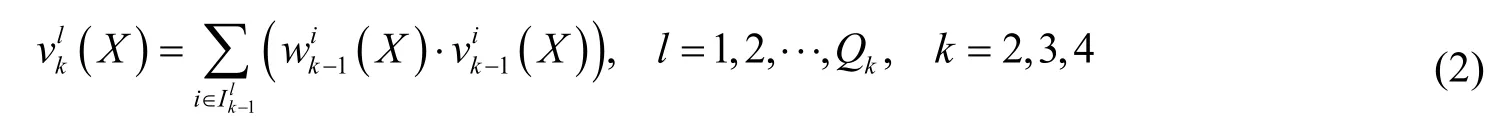
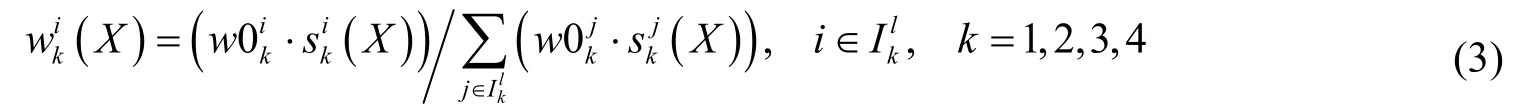
2 物流網絡變權路徑選擇及貨流分配
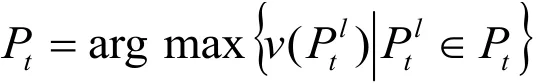
3 算例分析
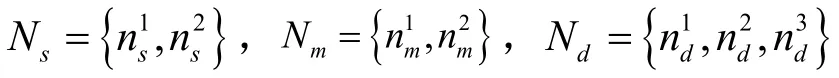

表1 節點線路屬性參數Table 1Attribute parameters of nodes and lines
3.1 屬性層的狀態與變權
3.1.1 節點屬性狀態與變權計算 供應節點、需求節點和中間節點屬性值向量分別為:
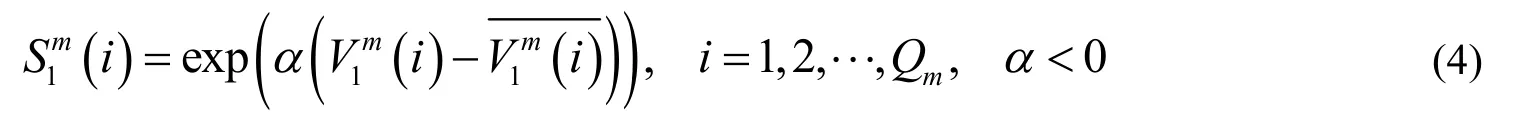
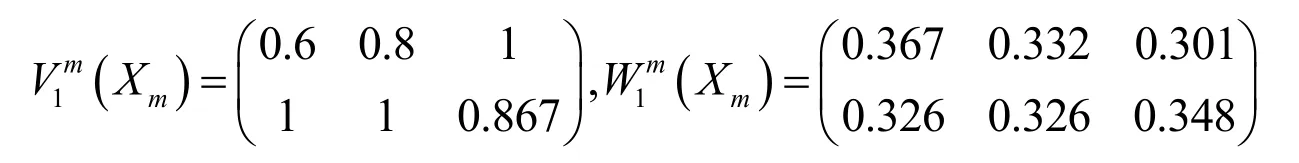
由此可見,對于中間節點,其飽和度、時間和成本三個屬性的權重并非固定不變,而是隨著每一輪次貨流量分配的變化,屬性狀態值會發生改變,結合決策者的偏好,各屬性權重不斷調整。其他各層要素的權重分配亦是如此。
3.1.2 線路屬性狀態與變權計算 線路屬性值向量定義為:
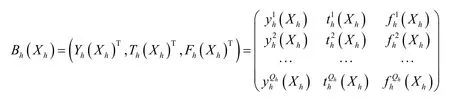
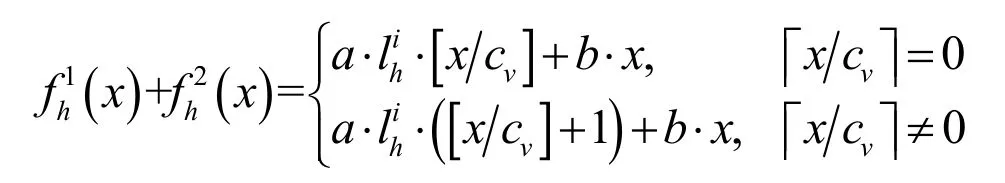
3.2 節點線路層、子路徑層和總路徑層的狀態與變權
根據物流網絡層次變權模型,除了最底層的屬性層,其余各層因素的狀態值都是由直接下層中相關屬性因素的狀態值及變權來決定,如式(2)所示。本算例中,對節點線路層和子路經層進行評價時,我們考慮其構成屬性的均衡性,故采用懲罰型狀態變權函數,如式(4)所示;而對總路徑層,由于在一級路徑和二級路徑中實施的干線運輸和支線運輸分別耗費的時間和成本具有較大差異,因此在進行子路經權重調整時,更側重對一級路徑的考慮,故采用如式(5)所示的激勵型狀態變權函數進行變權計算。
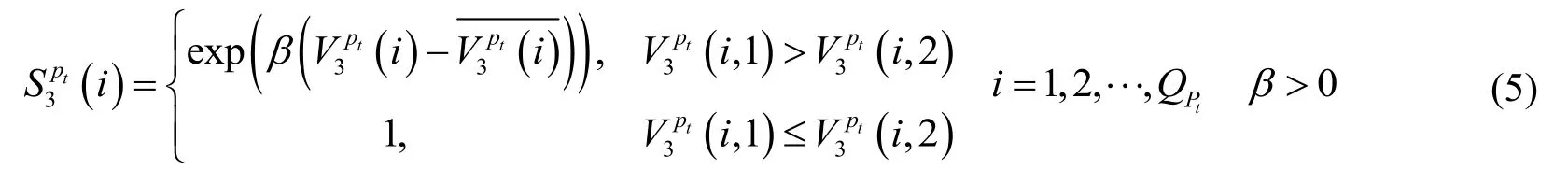
3.3 總路徑選擇及貨流量分配
通過3.1和3.2小節的計算,最終得到物流網絡中所有總路徑的狀態值如表2所示。

表2 總路徑狀態值Table 2 State values of whole paths
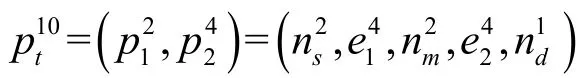
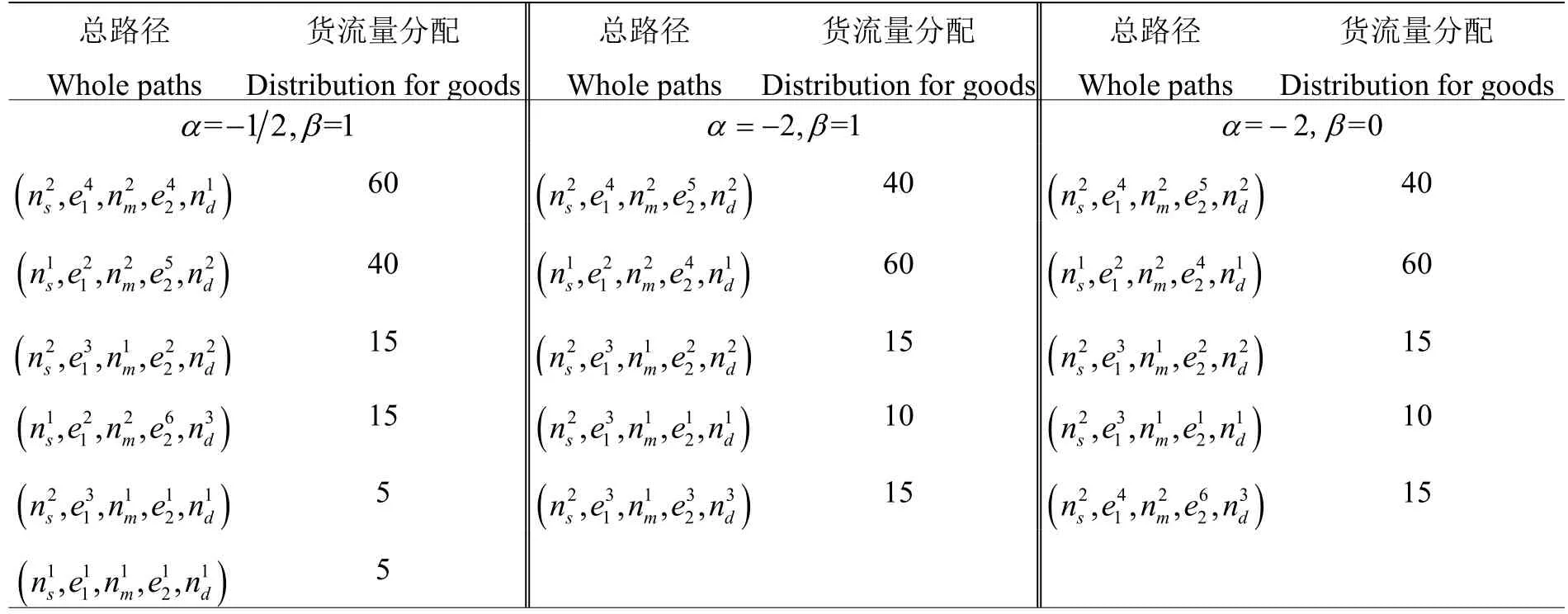
表3 總路徑選擇及貨流量分配結果Table 3 Whole path selection and freight flow distribution
4 結論
在物流網絡路徑選擇并進行貨流量分配決策時,單一的常權的路徑度量方式不能體現現實物流網絡的動態特性。本文構建物流網絡層次變權模型,研究各層因素的動態變化與決策者的決策意愿影響下的因素變權方法,以多因素的變權綜合描述物流網絡總路徑,并在此基礎上得到貨流量的分配方式。該方法不僅避免了以往路徑選擇方法中影響因素的不可替代性,增強了決策方法的科學性,而且將決策者意愿充分體現在決策過程中,使決策方法更具實用價值。
[1]Tajdin A,Mahdavi I,Mahdavi-Amiri N,et al.Computing a fuzzy shortest path in a network with mixed fuzzy arc lengths using α-cuts[J].Computers and Mathematics with Applications,2010(4):989-1002
[2]Ioachim I,Gélinas S,Soumis F,et al.A dynamic programming algorithm for the shortest path problem with time windows and linear node costs[J].Networks,2015,31(3):193-204
[3]Santos L,Coutinho-Rodrigues J,Current JR.An improved heuristic for the capacitated arc routing problem[J].Computers&Operations Research,2009(9):2632-2637
[4]W?stlund J.Random assignment and shortest path problems[J].Dmtcs Proceedings,2015(S):1-1
[5]Wu X,Nie Y.Implementation Issues for the Reliable A Priori Shortest Path Problem[J].Transportation Research Record Journal of the Transportation Research Board,2016,2091:51-60
[6]Lin YK.Time version of the shortest path problem in a stochastic-flow network[J].Journal of Computational and Applied Mathematics,2009(1):150-157
[7]李引珍,何瑞春,郭耀煌.結點有約束的交通網絡最短路徑模型[J].運籌與管理,2005(4):40-43
[8]韓世蓮,劉新旺,HANShi-lian,等.物流運輸網絡多目標最短路問題的模糊滿意解[J].運籌與管理,2014(5):55-61
[9]溫惠英,沈毅賢.基于層次分析法的物流配送車輛導航路徑規劃求權方法[J].公路交通科技,2008(8):114-118
[10]周 曉,張 錦,張 菲,等.基于變權的多目標物流網絡貨流分配方法[J].西南交通大學學報,2012,47(1):151-157
[11]余高鋒,劉文奇,石夢婷.基于局部變權模型的企業質量信用評估[J].管理科學學報,2015(2):85-94
[12]李德清,郝飛龍.狀態變權向量的變權效果[J].系統工程理論與實踐,2009(6):127-131
[13]李德清,曾文藝.變權決策中均衡函數均衡效果[J].系統工程理論與實踐,2016,36(3):712-718
[14]余高鋒,李登峰,劉文奇.考慮決策者心理行為特征的激勵型變權決策方法研究[J].系統工程理論與實踐,2017,37(5):1304-1312
[15]Li DQ,Hao FL,Mathematics D.Variable weights multifactor decision making based on linguistic factor state values[J].Systems Engineering-Theory&Practice,2014,34(1):176-181

