四旋翼無人機懸停飛行自適應PD控制器設計

李艾棠， 譚功全， 郭金虎

(四川理工學院自動化與信息工程學院， 四川自貢643000)

四旋翼無人機懸停飛行自適應PD控制器設計

李艾棠， 譚功全， 郭金虎

(四川理工學院自動化與信息工程學院， 四川自貢643000)

提出一種基于模型參考的自適應PD控制器設計方法，用于質量可變的四旋翼無人機的懸停飛行控制。由無人機的動力學方程對懸停飛行時姿態角近似處理得出參考模型，根據參考模型選取一個與實際系統相似并且有期望動態特性的二階系統。基于Lyapunov穩定性理論的方法，通過被控對象的輸出與參考模型輸出之間的誤差確定控制器的參數，當被控對象參數發生變化時，自適應機構通過參數估計調整PD控制器的輸出，使被控對象參數的估計值總能跟蹤其實際值，并分別與常規的PD控制器和加入了限速補償環節的PD控制器進行仿真實驗對比。結果表明，該控制器的控制信號比常規的PD控制器超調量小；比加入了限速補償環節的PD控制器調節速度快，穩定性更好。對于四旋翼無人機的懸停有更好的控制效果。

四旋翼無人機；比例微分控制器；懸停飛行；自適應

引言

四旋翼飛行器結構簡單、機動性強、靈活性高，一般有定高、繞圈、懸停等多種飛行模式，可以飛至離目標更近的區域進行懸停，不像傳統的大型直升機由于巨大的旋翼而不能靠近目標，也不像傳統固定翼飛行器不能懸停[1]。而懸停模式作為最簡單的一種飛行模式，通常被用作實驗模式以獲取無人機的某些動力學參數以及驗證控制器的可靠性。無人機在懸停過程中其傾斜角為零，不需要考慮水平方向上的運動[2]，因此其動力學模型可以作簡單的線性化處理。

四旋翼無人機的控制方法主要有：PID控制[3-4]、滑模控制[5](Sliding-Mode)、反步法[6-8](Backstepping)、線性二次型[9-10](LQ)、神經網絡自適應[11]、反饋線性化[12-13](Feedback Linearization)以及H∞[14-15]控制等。

在軍事偵察、日常航拍、氣象監測、森林防火這些領域的應用時，無人機動力學參數基本是不發生變化的，對于這樣的情況使用常規的控制方法設計的控制器已經能夠很好地控制無人機的飛行，但在某些實際應用領域中，無人機的動力學參數是會發生變化的，如噴灑農藥的無人機，其質量會隨著農藥量的減少而減小；運送快遞包裹的無人機質量也會隨著包裹的質量不同而不同，同時它們繞機體坐標系三軸旋轉的轉動慣量也會隨著質量的變化而變化。這時無人機系統將變為時變系統，常規的PD控制器已經不能很好地對其進行控制，那么就需要一種更好的方法來設計控制器。

本文采用自適應控制理論與PD控制器相結合的方法設計出了一種模型參考自適應PD控制器(Model Reference Adaptive PD Controller)用于質量可變的四旋翼無人機的懸停控制，并對其進行了Matlab/Simulink仿真，進一步驗證了這種控制器的效果。

1 四旋翼無人機的動力學模型

四旋翼無人機的動力學模型可通過牛頓-歐拉方法[16]、歐拉-拉格朗日方法[17]、四元數法[18]等多種方法建立，本文不再贅述。忽略空氣阻力，在小角度條件下四旋翼無人機的近似動力學數學模型可以表示為：

(1)

式中：x、y、z表示無人機的質心在慣性坐標系中的坐標；φ、θ、ψ表示無人機的三個傾斜角，m表示無人機的質量，b表示螺旋槳的升力系數；τφ、τθ、τψ分別表示偏航力矩、俯仰力矩和滾轉力矩；Ωi(i=1,2,3,4)表示四個旋翼的旋轉角速度。

四旋翼無人機懸停時θ≈0、φ≈0，其飛行高度近似滿足：

(2)

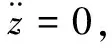
(3)

將式(3)代入式(2)，得：

(4)

記無人機的控制輸入為：

(5)

式中k0的值與輸出信號的占空比相關。

聯立式(4)與式(5)，得：

(6)

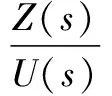
(7)

此即為四旋翼無人機系統在懸停模式下的傳遞函數。

2 模型參考自適應PD控制器設計

2.1 模型參考自適應PD控制的原理

模型參考自適應控制系統的基本結構如圖1所示，它由兩部分組成：由控制器和被控對象組成內環，由參考模型和自適應機構組成外環。實際上就是在常規的負反饋控制回路上并聯一個參考模型以及自適應控制器[19]。

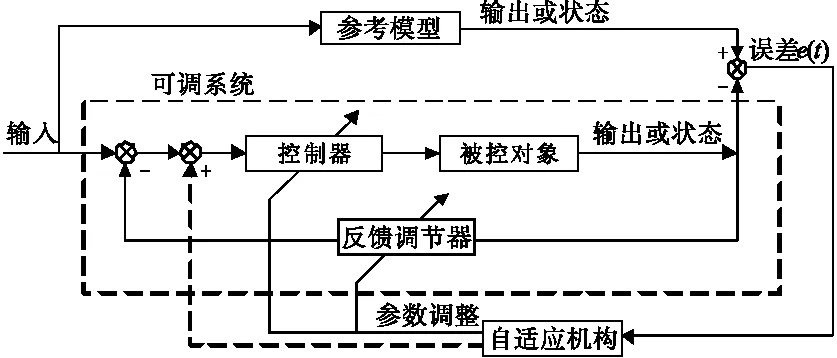
圖1模型參考自適應控制系統

在該控制系統中，被控對象的參數是不確定或可以發生改變的，控制器有一個初始參數，而參考模型是一個具有較好動態及靜態特性的系統，將目標信號同時作用在控制器及參考模型上，對被控對象的輸出或狀態及參考模型的輸出模型及狀態進行比較，將它們的誤差信息按照一定的規律計算，產生一個輔助的輸入信號或產生控制器的參數變量[20]。目的是使得被控對象的輸出能夠盡可能地跟蹤參考模型的輸出，當被控對象的參數發生變化或系統受到外界干擾使得輸出偏離平衡位置時，誤差將會增大，這時自適應機構再次調整控制系統的參數使得被控對象的輸出再次趨近于參考模型的輸出。

模型參考自適應控制器設計的核心是通過被控對象的輸出與參考模型的輸出之間的誤差確定控制器的參數，有兩種方法：一種是利用優化方法尋找控制器的最優參數，使得系統滿足某個評價指標，通常使用的指標是使J達到最小：

(8)

另一種方法是基于穩定性理論保證控制系統的穩定性，通常用的是基于Lyapunov穩定性理論的設計方法，本文通過第二種方法來確定控制器的參數。

2.2 模型參考自適應PD控制器的數學模型

設計了一種基于期望動態特性的PD控制器來控制四旋翼無人機的飛行高度，控制對象為二階積分過程，控制系統的閉環特征方程為：

(9)

期望的閉環特征方程為：

(10)

聯立式(9)、式(10)可得：

(11)

PD控制器的參數kc及kd與被控對象的參數k相關，由式(11)可知，總能找到合適的kc及kd，使得控制系統具有期望的動態響應，當被控對象參數k發生變化時，自適應機構通過對其進行估計來自適應調整PD控制器的輸出。

由式(7)知，參考模型選取一個與實際系統相似并且有期望動態特性的二階系統，參考模型中的被控對象參數不變，其結構如圖2所示。

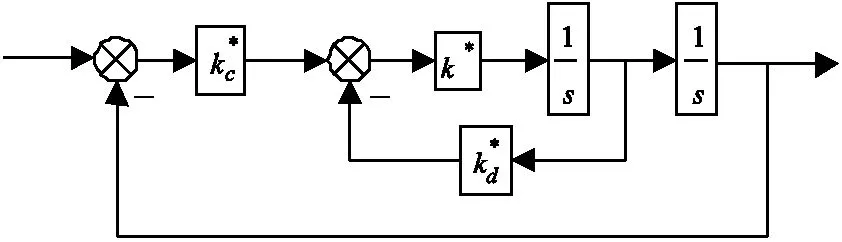
圖2參考模型的結構

基于式(10)的期望動態特性的PD控制器增益與被控對象的參數滿足如下關系：

(12)

故，參考模型的結構可簡化為圖3所示。

該系統的閉環傳遞函數為：

(13)

對應的微分方程為：

(14)

取系統的狀態變量為：

x1d=y

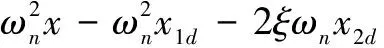
(15)

式中，x為系統輸入，y為系統輸出。

同理，實際的控制系統的結構如圖4所示。

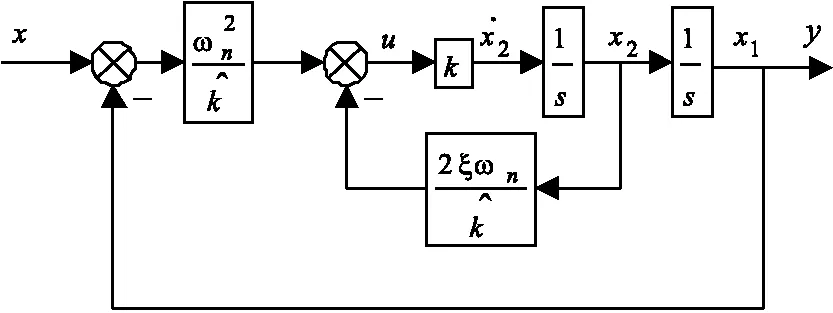
圖4實際系統的結構

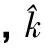
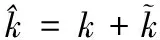
(16)

實際控制系統的閉環傳遞函數為：

(17)

對應的微分方程為：

(18)

取系統的狀態變量為：

x1=y

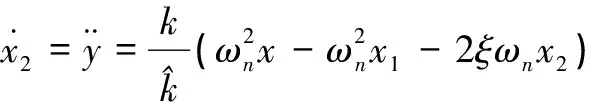
(19)

PD控制器的控制輸出為：

(20)

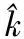
(21)

對式(21)兩端求導，得：

(22)

構造Lyapunov函數：

(23)

對式(23)兩端同時求導，得：

(24)

(25)

所以，被控對象的參數估計值為：

(26)

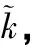
2.3 受干擾時的懸停控制

無人機在飛行過程中受到的外界干擾主要為風力干擾及電磁干擾。電磁干擾可以視為一種白噪聲干擾，可在姿態解算時通過濾波加以消除，而影響無人機飛行高度的風力干擾主要是發生在下擊暴流天氣中的向下氣流[21]。下擊暴流是一大團下降到地面的冷空氣，當這些氣流接近地面是，氣流改變方向，向外輻射流出。由于下擊暴流是一種不可預測的天氣現象，若無人機在飛行過程中遇到這種天氣，可認為是無人機的質量發生了改變，這和我們設計之初提出的理念一樣。而當無人機遇到側風干擾時，無人機的姿態發生變化，即無人機的姿態角發生變化(主要為偏航角)，這時自適應機構通過控制姿態角對無人機的姿態進行修正，使之繼續保持懸停。下面主要分析對偏航角的控制。

單獨對無人機只有偏航角發生變化時，俯仰角、橫滾角近似不變，且滿足俯仰角θ≈0，橫滾角φ≈0，無人機偏航運動的動力學方程為：

(27)

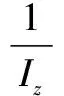
(28)

偏航角的控制器的控制率為：

(29)

傳遞函數為：

(30)

參數整定方法同上，參數整定結果為：

(31)

從式(31)可以看出，自適應機構對偏航角的控制類似于高度控制，總可以使控制參數估計值跟蹤其真實值，進而對偏航角進行修正，姿態恢復。

3 仿真驗證

對該系統設計Matlab仿真，用階躍信號加方波信號來表示期望高度，用斜波信號加方波信號來表示被控對象的實際參數變化，Lyapunov函數中的參數γ=0.1，參考模型的阻尼比ξ=0.9，無阻尼自然頻率wn=2[22]，被控對象的參數在誤差范圍內的近似值0.025，仿真結果如圖5所示。

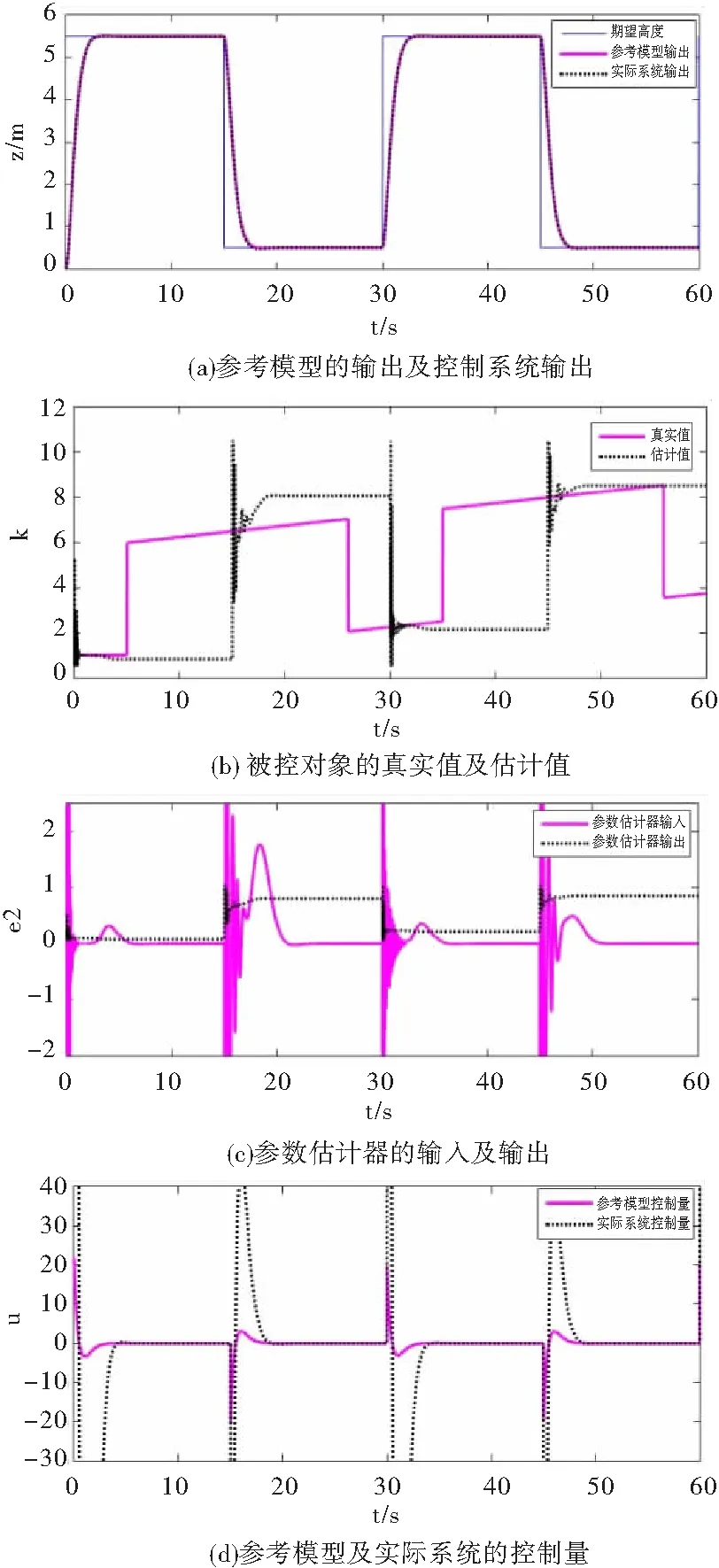
圖5模型參考自適應PD控制系統仿真結果

圖5(a)表示輸入系統的期望高度以及參考模型及實際系統的響應輸出，從響應結果來看，實際控制系統能很好地跟蹤參考模型的輸出，模型參考選取的正確性進一步得到驗證。

圖5(b)表示被控對象的參數k的真實值及估計值，當實際控制系統與參考模型之間有誤差時，參數估計器開始計算被控對象的實際參數，當誤差為零時被控對象的參數不被修正，也說明當無人機質量發生變化時，即k發生變化，自適應系統產生的估計值總能夠跟蹤k的值，對無人機進行懸停控制。

圖5(c)表示參數估計器的輸入及輸出，輸入為參考模型與實際控制系統的狀態變量之間的誤差，輸出為被控對象的參數值，

圖5(d)為參考模型及實際系統的控制量，結合仿真結果可知，當實際系統與參考模型的輸出之間無誤差時，被控對象參數的估計值不會更新，而當實際系統與參考模型的輸出之間出現誤差時，參數估計器才會對被控對象參數進行估計，從而改變控制器的輸出。

在實際的控制過程中，同樣存在輸入飽和的問題，將本文設計的模型參考自適應PD控制器(記為PD1)分別與常規PD控制器(記為PD2)及加入限速補償環節的PD控制器(記為PD3)進行比較，用三者分別對四旋翼無人機的飛行高度進行控制，設定期望高度為20 m，無人機電機轉速的安全范圍設定為700～1000 rpm，在Matlab中進行仿真，仿真結果如圖6所示。

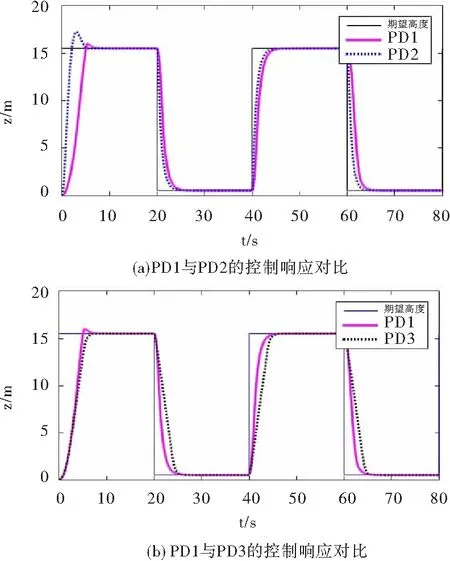
圖6幾種PD控制器的比較

圖6(a)為模型參考自適應PD控制器與常規PD控制器的控制響應對比，顯然，常規的PD控制器有較大的超調，對于期望的懸停控制高度有較大的波動，對于精度要求較高的場合，懸停高度可能在超調階段已經超出實際允許的范圍，顯然模型參考自適應PD控制器效果更好；圖6(b)為模型參考自適應PD控制器與加入限速補償環節的PD控制器的控制響應對比，由仿真結果可知，二者的調節時間基本相等，加入限速補償環節的PD控制器的調節過程較平緩，控制信號對無人機懸停高度控制緩慢，因而無人機姿態調整較平緩、時效性差，而模型參考自適應PD控制器雖然在調節前期有很快的調節速度，但為防止過大超調，在調節后期速度稍微放緩，綜合而言，模型參考自適應PD控制器對懸停高度控制有更好的效果。

4 結束語

本文考慮一類時變系統的自適應控制，被控對象是動力學參數可變的四旋翼無人機的飛行高度，采用了模型參考自適應PD控制的方法，對控制器的原理進行了介紹，并設計了適用于四旋翼無人機懸停控制的控制器[23]。

模型參考自適應控制器選擇具有較好響應的二階系統作為參考模型，基于Lyapunov穩定性理論對被控對象的參數進行了估計，利用估計的參數對PD控制器進行自適應校正，從Matlab仿真結果可以看出，本文設計的控制器對四旋翼無人機的飛行高度有很好的控制效果。

[1] CAPELLO E,SCOLA A,GUGLIERI G,et al.Mini quadrotor UAV:design and experiment[J].Journal of Aerospace Engineering,2012,25(4):559-573.

[2] 楊瑞,王小麗,王強,等.風力機尾流場及相互作用的實驗研究[J].四川理工學院學報:自然科學版,2015,28(4):11-16.

[3] SALIH A,MAHMOUD M,MOHAMED H,et al.Flight PID Controller design for a UAV quadrotor[J].Scientific Research and Essays,2010,5(23):3660-3667.

[4] ERGINER B,ALTUG E.Modeling and PD control of a quadrotor VTOL vehicle[C]//Proceedings of the 2007 IEEE Intelligent Vehicles Symposium,Istanbul,Turkey,June 13-15,2007:894-899.

[5] DIERKS T,JAGANNATHAN S.Neural network output feedback control of a quadrotor UAV[C]//Proceedings of the 47thIEEE Conference on Decision & Control,Cancun,Mexico,December 9-11,2008:3633-3639.

[6] 聶博文.微小型四旋翼無人直升機建模及控制方法研究[D].長沙:國防科學技術大學,2006.

[7] K?KSAL N,HAO A N,FIDAN B.Two-Level nonlinear tracking control of a quadrotor unmanned aerial vehicle[J].Ifac Papersonline,2016,49(17):254-259.

[8] AL-HIDDABI S A.Quadrotor control using feedback linearization with dynamic extension[C]//Proceeding of the 6th International Symposium on Mechatronics and its Applications(ISMA09),Sharjah,UAE,March 23-26,2009:82-84.

[9] BOUABDALLAH S,NOTH A,SIEGWAN R.PID vs LQ control techniques appliedto an weight augmentation high energy conruniption indoor micro quadrotor[C]//Proceedings of 2004 IEEE/RSJ International Conference On Intelligent Robots and Systems,Sendai,Japan,September 28-October 2,2004:2451-2456.

[10] BAUER P,RITZINGER G,SOUMELIDIS A,et al.LQ servo control design with Kalman filter for a quadrotor UAV[J].Periodica Polytechnica Transportation Engineering,2008,36(5):9-14.

[11] DAS A,LEWIS F,SUBBARAO K.Backstepping approach for controlling a quadrotor using Lagrange form dynamics[J].Journal of Intelligent & Robotic Systems,2009,56(1-2):127-151.

[12] LEE D,KIM H J,SASTRY S.Feedback linearization vs adaptive sliding mode control for a quadrotor helicopter[J].International Journal of Control Automation & Systems,2009,7(3):419-428.

[13] BOROUJENI Z,MOHAMMADI M,BOROUJENI S,et al.Adaptive feedback linearizing tracking control of a quadrotor helicopter[C]//Proceedings of the 2nd International Symposium on Computing in Science and Engineering,Izmir,Turkey,June 1-4,2011:2035-2041.

[14] Mokhtari A,Benallegue A,Daachi B.Robust feedback linearization and GH∞ controller for a quadrotor unmanned aerial vehicle[J].Journal of Electrical Engineering,2006,57(1):20-27.

[15] RAFFO G V,ORTEGA M G,RUBIO F R.An integral predictive/nonlinear H∞ control structure for quadrotor helicopter[J].Automatica(Journal of IFAC),2010,46(1):29-39.

[16] FERMI G,NICOLAS M,AHMAD H,et al.Bounded attitude control of rigid bodies:Real-time experimentation to a quadrotor mini-helicopter[J].Control Engineering Practice,2011,19(8):790-797.

[17] 丁少賓,肖長詩,劉金根,等.X型四旋翼無人機建模及四元數控制[J].系統仿真學報,2015,27(12):3057-3062.

[18] ANEZKA C,TOMAS F,LUBOS C,et al.Mathematical modelling and parameter identification of quadrotor[J].Procedia Engineering,2014,96:172-181.

[19] 朱冰.四旋翼飛行器的模型參考自適應控制研究[J].計算機測量與控制,2014,22(6):1745-1776.

[20] 楊艷萍,張大偉.基于粒子群優化設計算法的輸出跟蹤控制[J].自動化技術與應用,2016,35(1):8-13.

[21] ROGELIO L.Unmanned aerial vehicles:embedded control[M].New Jersey:John Wiley & International Rights Sons,Inc,2010.

[22] 陳永會,譚功全,沈勇.阻尼比約束的時滯系統最優PI調節器設計[J].控制工程,2015,22(4):720-724.

[23] 魏青銅,陳謀,吳慶憲.輸入飽和與姿態受限的四旋翼無人機反步姿態控制[J].控制理論與應用,2015,32(10):1361-1369.

Design of Hover Flying Adaptive PD Controller for Four Rotor Unmanned Aerial Vehicle

LIAitang,TANGongquan,GUOJinhu

(School of Automation & Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)

An adaptive PD controller design method based on model reference is proposed, which is used to control the suspension of the four rotorcraft with variable quality. The reference model is obtained by approximating the attitude angle of the hovercraft by the kinetic equation of the UAV, and a second order system is selected according to the reference model which is similar to the actual system and has the expected dynamic characteristics. Based on the method of Lyapunov's stability theory, the parameters of the controller are determined by the error between the output of the controlled object and the output of the reference model. When the controlled object parameter changes, the PD controller is adjustedby parameter estimation of the adaptive mechanism, so the estimated value of the controlled object parameter can always track its actual value. The conventional PD controller and the PD controller with the speed limit compensation are compared with it respectively.The results show that the control signal of the controller is smaller than that of the conventional PD controller. It is faster and more stable than the PD controller with the speed limit compensation,and also has a better control effect for the four-rotor UAV hover.

four-rotor unmanned aerial vehicle; proportional differential controller; hover flight; adaptive

1673-1549(2017)06-0054-07

10.11863/j.suse.2017.06.10

2017-09-06

四川省教育廳科研基金(12ZA097;14ZA0205)

李艾棠(1991-),男,四川德陽人,碩士生,主要從事電力系統及智能控制方面的研究,(E-mail)565562454@qq.com

譚功全(1970-),男,重慶壁山人，教授,主要從事控制理論及其應用、嵌入式系統及其應用等方面的研究。

TP13

A