三角變換的常用方法

饒子揚

(河北省唐山市第二中學(xué) 063000)

三角變換的常用方法

饒子揚

(河北省唐山市第二中學(xué) 063000)

三角題的形式多樣，解題方法靈活多樣.本文就三角解題中的常用方法——代換法，加以分類例析，供同學(xué)們參考.

三角解題；代換；方法

求解三角問題時，根據(jù)題目特點，常需要考慮選擇恰當(dāng)?shù)姆椒ǎ故阶雍喕瑔栴}明朗，進而容易獲解.本文就常用的變換分類舉例加以說明，參考教科書是人教版課標(biāo)數(shù)學(xué)4必修.

一、“1”的代換

利用常數(shù)代換1=sin2α+cos2α,1=tan45°等可把常數(shù)寫成三角式，為利用三角公式解題帶來便利.

二、平均值代換

三、對偶代換

在三角式中，我們稱f(sinx)與f(cosx)互為對偶式，利用兩個對偶式的和、差、積、平方和等，可簡化式子.

例3 (教科書P138頁B3題)求sin220°+cos250°+sin20°cos50°的值.

解記A=sin250°+cos250°+sin20°cos50°,

構(gòu)造對偶式B=cos220°+sin250°+cos20°sin50°.

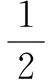
四、字母代換

將某些三角函數(shù)式用一個字母表示，可以化復(fù)雜的三角式為代數(shù)式，明晰字母間的數(shù)量關(guān)系，回避復(fù)雜的三角公式的變換，從而優(yōu)化解題.

例4 求sin54°-sin18°的值.

解記x=sin54°=cos36°,y=sin18°=cos72°.由cos72°=2cos236°-1,得y=2x2-1.又cos36°=1-2sin218°=1-2cos272°,故有x=1-2y2.

所以x+y=2(x2-y2)=2(x+y)(x-y).

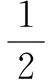
五、三角代換

將題目中的三角式再進行三角代換，可簡化原來的三角式，開辟新的解題思路.

六、整體代換

將待求的較復(fù)雜的式子設(shè)為一個字母，可簡化表達形式，方便解題.

[1]陳京敖.一道課本例題的高考變式之路[J].中學(xué)數(shù)學(xué)，2014(2)：48-50.

[2]張建虎.用角代換解三角題[J].中學(xué)生數(shù)學(xué)，2010(11)上：17～18.

[3]張銳.一個問題的誤解辨析[J].中學(xué)生數(shù)學(xué)，2010(12)上：42～43.

G632

A

1008-0333(2017)31-0037-02

2017-07-01

饒子揚，河北省唐山市第二中學(xué)，高二學(xué)生.

楊惠民]