談談判別式的解題功能

常思源

(河北省唐山市第二中學 063000)

談談判別式的解題功能

常思源

(河北省唐山市第二中學 063000)

在高中數(shù)學學習中，注重數(shù)學思想方法的學習和總結，掌握多種多樣的數(shù)學方法，這對提高解答數(shù)學問題的能力是十分重要的.本文針對數(shù)學解題中應用廣泛的“判別式”法，列舉了它的多種用途，這對提高解題能力具有參考價值.

數(shù)學解題；一元二次方程；判別式；功能

一、求值域

例1 已知實數(shù)a、b、c滿足a+b+c=0,a2+b2+c2=1,則a的取值范圍是____.

解將c=-(a+b),代入a2+b2+c2=1中，消去c，再以b為主元，a為參數(shù)整理成2b2+2ab+2a2-1=0.

將上式視為關于b的一元二次方程，由b是實數(shù)，知該一元二次方程有實根，故Δ=4a2-8(2a2-1)≥0.

點評本例解法中，先消去(c)化三元為二元，再選定主元(b)和待求參數(shù)(a)，從而構造出一元二次方程，利用判別式非負使問題獲解.以上的解題思路自然順暢，是我們解答數(shù)學題的常規(guī)策略，是我們每個高中生都應掌握的基本技能.

二、求最值

例2 曲線x2-2xy-3y2=1上的點到坐標原點的距離的最小值為____.

由t(x2-2xy-3y2)=x2+y2,整理成(t-1)x2-2txy-(3t+1)y2=0.

(1)當y=0時，可求得t=1.

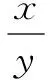
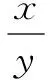
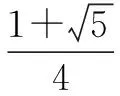
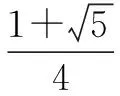
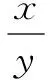
三、證明不等式

例3 設a、b是實數(shù)，且a3+b3=2,求證0

而上式中的k2+2k+4的判別式Δk=22-4×1×4=-12<0,故恒有k2+2k+4>0,那么不等式化成k(k-2)≤0(k≠0).

解得0

點評本例解題中先從條件式中通過引入?yún)?shù)k來表達a+b，ab，從而逆用韋達定理構造出一元二次方程，為利用判別式創(chuàng)造了條件.但解題中應關注一些隱含條件(k≠0)(k2+2k+4>0)，才能使解題即嚴謹又簡化.

四、求參數(shù)的值

Δ1=a2-4(b+1)≥0且Δ2=a2-16(4-b)≥0①.

Δ1=a2-4(b+1)≤0且Δ2=a2-16(4-b)≤0②.

由①和②可知有

點評本解法對值域[-1,4]的深層次含義進行挖掘，分別利用方程有實根和不等式恒成立，從兩個方面思考，列出兩個判別式的不同符號，從而導出兩個判別式都為零，充分體現(xiàn)了思維的靈活與廣闊性，對判別式的含義理解深邃.

總之，判別式的應用是十分廣泛的，以上僅對代數(shù)方面的應用略談幾例，實際上，判別式在幾何、三角、解析幾何等諸多方面都有應用.可以說，判別式法是求解數(shù)學問題常用的、廣泛的、重要的工具，我們應熟練掌握，善于運用.

[1]趙建勛.判別式法解題舉例[J].中學生數(shù)學(高中)，2014(1)：15-16.

[2]趙興根.例析反向思維在初中數(shù)學解題中的應用[J].福建中學數(shù)學，2014(3)：42.

[3]楊春娟.含參一元二次不等式的解法與恒成立問題[J].中學生數(shù)學(高中)，2015(2)：28.

G632

A

1008-0333(2017)31-0040-02

2017-07-01

常思源，河北省唐山市第二中學，在校學生.

楊惠民]