用構造法巧解不等式問題
母賀楠
(河北省唐山市樂亭縣第一中學 063600)
用構造法巧解不等式問題
母賀楠
(河北省唐山市樂亭縣第一中學 063600)
在高中三年的學習中,我們學到了許多數學知識.如何將知識轉化為能力,成為我們解決問題的工具,針對這一問題,本文僅就不等式問題的求解,談些認識與體會.
構造法;不等式問題;模型
構造法是對數學知識的開拓性、創造性運用,對發展數學思維,提升數學素養有著重要的作用.本文僅就不等式(最值)的有關問題,說明構造數學模型的若干途徑.
一、構造相應函數
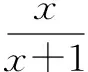
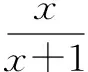
點評函數是高中數學知識的主線.根據題目中式子的特征,構造相應的函數模型,利用函數的性質(單調性,奇偶性,最值)解題,是最基本最重要的方法.
二、構造方程
例2 設x,y為實數,若4x2+y2+xy=1,則2x+y的最大值為____.
解令2x+y=k,即y=k-2x,代入已知式,整理得6x2-3kx+k2-1=0.
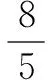
點評根據解題需要構造出相應的方程,是常用方法.構造的途徑有利用根的定義,韋達定理,判別式等.
三、構造三角式
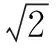
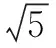
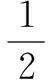
點評本題的常規解法是用直線方程與圓的方程聯立,求出弦長,再求面積的最大值,十分煩瑣.而上述解法恰當引入角變量θ,轉化為三角式問題,解法巧妙簡捷.
四、構造數列
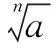

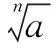
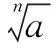
點評將待證式變形后,逆向思維,觀察出分式是等比數列前n項和,通過構造相關數列,使問題簡捷獲解.
五、構造二項式
例5 求證2n>2n+1(n∈N*且n≥3).
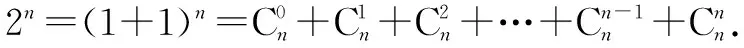
由n≥3知展開式至少有4項,故
點評以上證明不用常規的數學歸納法,而巧構二項式,速證不等式.
六、構造向量
例6 設x、y、z>0,xyz=1,求證
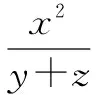
分析將左邊各分式看成某式的平方,來構造兩個向量的模與數量積,然后利用模與數量積的不等式求解.
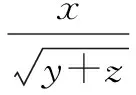
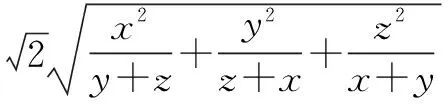
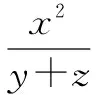
構造法解題是以堅實的基礎知識為根基的,通過敏銳的觀察,廣泛的聯想來實現的.這需要平時的積累.
[1]張志兵.例談“構造法”在高中數學解題中的應用[J].數學教學研究,2013(7).
[2]蘇亦亞.淺談“構造法”在高中數學解題中的運用[J].中學數學,2014(6):62~63.
[3]孫春生.構造法中的奇葩[J].中學生數學,2010(11):39~41.
G632
A
1008-0333(2017)31-0046-02
2017-07-01
母賀楠,河北省唐山市樂亭縣第一中學,高三學生.
楊惠民]

