突破中學數(shù)學“假性理解”的“三維思考”

朱云虎

(江蘇省南通市通州區(qū)金沙中學 226500)

突破中學數(shù)學“假性理解”的“三維思考”

朱云虎

(江蘇省南通市通州區(qū)金沙中學 226500)

數(shù)學的體現(xiàn)形式有三種：文字形態(tài)，式子形態(tài)，圖象形態(tài)，這三種形態(tài)成為“數(shù)學三維”，巧妙的將這三者之間進行轉(zhuǎn)化，就可以構建起學生的數(shù)學能力.

文字；式子；圖象；數(shù)學三維；數(shù)學能力

中學數(shù)學中“假性理解”是一個比較普遍的現(xiàn)象，在不同的學生層次中均有表現(xiàn).具體的表現(xiàn)：學生常常發(fā)現(xiàn)無法獨立讀懂題意，解題過程中無法利用題中的條件等等.當教師在解讀題目的時候，學生常常又能自我的突破，為什么會出現(xiàn)這種情形？經(jīng)過多年比較，發(fā)現(xiàn)教師的思維方式和學生有很大的區(qū)別.教師比較關注于條件的自身分析，而學生卻更多地依賴于已有類試題的解題思路.本文就對教師的自身思維分析，來闡述“數(shù)學三維”的使用特點，以引導學生的思維生成.

一、三維的特征

1.文字的特殊性

文字是常見的信息的載體，是我們記載信息的一種重要的手段，可以確的表述某種客觀事實.它的缺點是“讓部分簡單的事實描述起來復雜化”，失去了某種簡潔性和直觀性.

2.式子的特殊性

式子是數(shù)學內(nèi)容表現(xiàn)的主要形式，也是學生解答解答題的主要形式.式子的最大優(yōu)點是嚴謹?shù)谋憩F(xiàn)數(shù)學的內(nèi)容，所謂的“0就是0，1就是1”，沒有言語誤解的可能性.缺點是式子過于抽象化，不易理解.

3.圖象的特殊性

圖象是體現(xiàn)數(shù)量關系和變量關系最好的載體，通過圖象我們可以清晰的看出量與量之間變化的過程，用圖象來體現(xiàn)數(shù)學具有直觀、明了.缺點是無法準確的表述兩個量之間的定性關系.

4.三維的關系

數(shù)學問題的具體體現(xiàn)通過文字的描述、式子的表達、圖象的直觀來表示數(shù)學相關的知識，這三種維度都是數(shù)學知識的具體體現(xiàn).但每個維度都有其優(yōu)點和缺點，如何通過三者之間的合理轉(zhuǎn)化利用其各自的優(yōu)點解決問題是我們解決數(shù)學問題的關鍵所在.

二、三維度之間的應用特點

1. 文字與式子之間的轉(zhuǎn)化

例1 已知一次函數(shù)f(x)滿足f(f(x))=4x+3，則f(x)= .

所以f(x)=2x+1或f(x)=-2x-3

評注題中一次函數(shù)的具體顯現(xiàn)f(x)=ax+b是解決這一問題的關鍵.

變式已知函數(shù)g(x)=x+1，二次函數(shù)f(x)滿足f(g(x))=x2+3x+3，則f(x)= .

例2 (2015年福建文科)若函數(shù)f(x)=2|x-a|(a∈R)滿足f(1+x)=f(1-x),且f(x)在[m，+∞)單調(diào)遞增，則實數(shù)m的最小值等于____．

解析由f(1+x)=f(1-x)得函數(shù)f(x)的圖象關于x=1對稱，由f(x)=2|x-a|可得圖象關于x=a對稱， 故a=1，則f(x)=2|x-a|.由復合函數(shù)單調(diào)性得f(x)在[1，+∞)遞增，故m≥1，所以實數(shù)m的最小值等于1．

評注本題思路的關鍵在于從函數(shù)式子中看出對應函數(shù)所要表達的內(nèi)涵：對稱性和單調(diào)性.從而使得信息明朗化，利于數(shù)學實際問題的解決.

2.文字與圖象之間的轉(zhuǎn)化

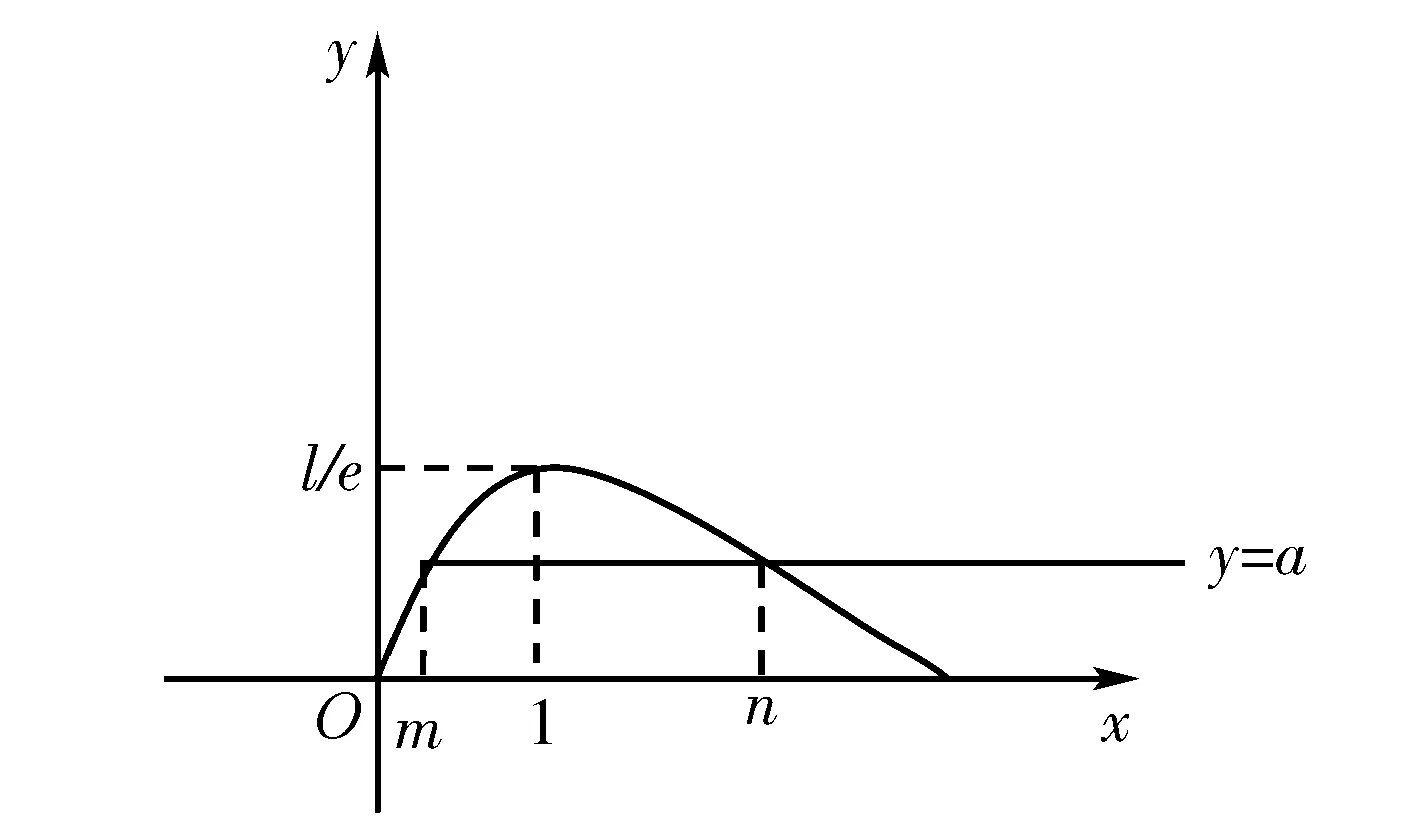
評注本題解決的關鍵是將題中的大量文字信息變成圖象信息，即作出表現(xiàn)意思的圖象.

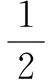
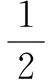
評注本題的關鍵在于從圖形中看出“同時函數(shù)圖象上的點到對稱軸的距離越大則相應的函數(shù)值越大”，從而正確的建立起|x1|>|x2|?f(x1)>f(x2)，解決問題.

3.式子與圖象之間的轉(zhuǎn)化

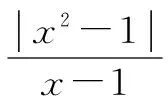
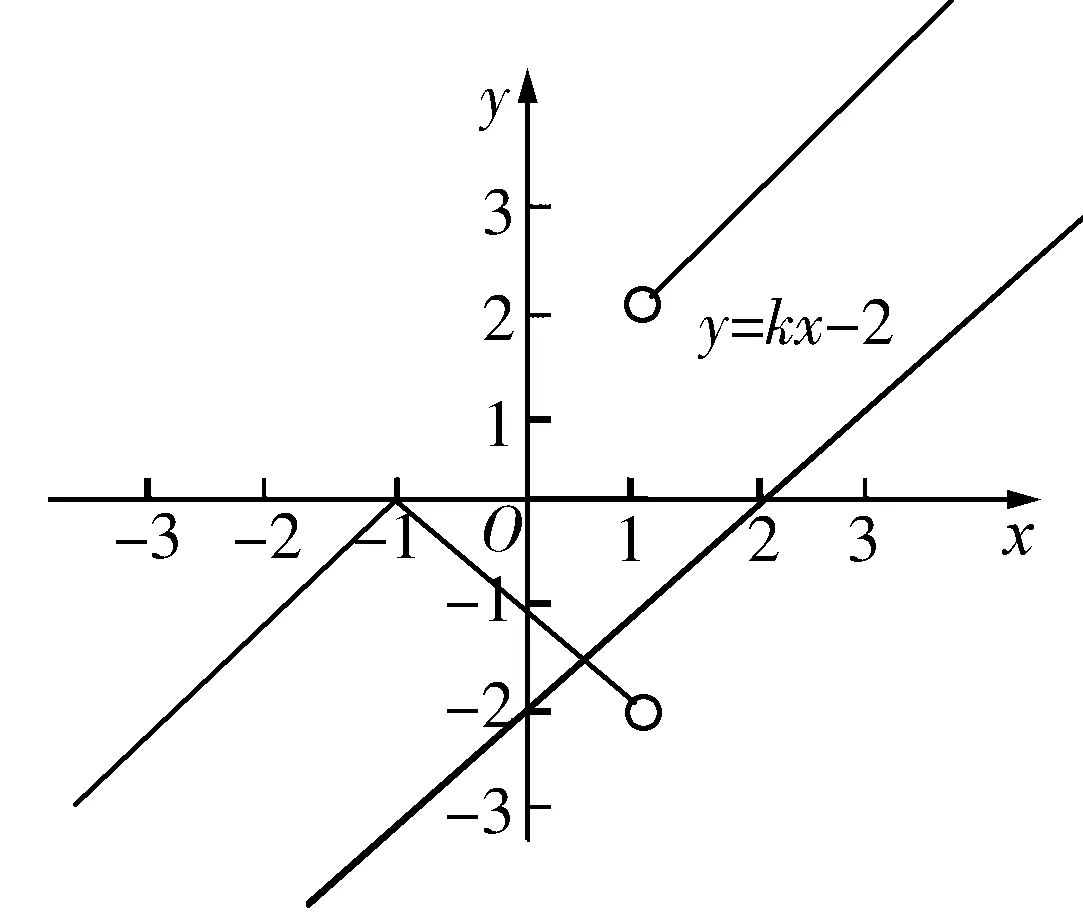
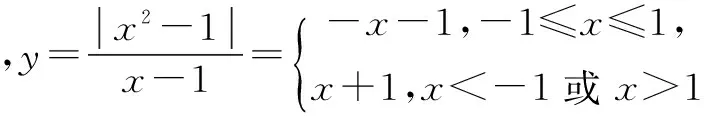
數(shù)學思維活動是一個嚴密的活動，更是一個開放的活動.它的基礎在于學生要求比較好的知識基礎，同時也要有豐富的聯(lián)想.其中的聯(lián)想其實就是對題中所涉及的知識點進行靈活的轉(zhuǎn)化，特別是三個維度之間的合理轉(zhuǎn)化，通過合理的轉(zhuǎn)化可以更為深刻的認識到知識的本質(zhì)，認識到知識在具體題中的應用要求，觸摸到各個知識點之間的交匯之處，從而生成解題的思路.因此，從某種意義上來說，學生對三維的處理能力代表著學生的解題能力，也代表著學生的思維水平.培養(yǎng)好學生的三維能力，是解決學生“假性理解”的一個重要舉措.

[1]單墫，等.普通高中課程標準實驗教科書必修1[M].南京：江蘇鳳凰教育出版社

G632

A

1008-0333(2017)31-0024-02

2017-07-01

朱云虎(1979.1-)，漢，本科，江蘇省南通人,中學一級教師，從事中學數(shù)學教學研究.

楊惠民]