探索關聯規則可視化的結構化關聯映射圖

易 黎 胡雅萌,2 彭艷兵

1(南京烽火軟件科技有限公司 江蘇 南京 210019) 2(武漢郵電科學研究院 湖北 武漢 430074)

探索關聯規則可視化的結構化關聯映射圖

易 黎1胡雅萌1,2彭艷兵1

1(南京烽火軟件科技有限公司 江蘇 南京 210019)2(武漢郵電科學研究院 湖北 武漢 430074)

對于大量的高維度的交易數據，利用關聯規則進行數據挖掘，用戶難以進行解釋和利用。主要兩個原因：常規關聯規則挖掘算法可產生大量關聯規則；一些關聯規則可部分重疊。若用戶能自主選擇，在關聯規則挖掘中所使用的相關項集，則可解決該問題。提出一種新的視覺探索工具，結構化關聯映射圖，使用戶能夠以視覺方式找到相關項集的組。該方法使用健康檢查結果數據集進行驗證，并且實驗結果表明具有最高2×2規則貢獻的和值的結構化關聯映射圖有助于顯著減少關聯分析的復雜性，并且能夠集中于搜索空間的特定區域關聯規則挖掘，同時避免不相關的關聯規則。

可視化 關聯規則挖掘 分層聚類 結構化關聯映射圖

0 引 言

隨著生活水平的提高，預防保健成為公眾關注的焦點，Boulware等[1]認為大眾健康檢查(MHE)在監測和評估個人健康水平方面發揮了重要作用，Kweon等[2]也提到MHE結果數據為在國家和個人層面制定衛生政策或戰略提供了堅實的基礎。邊根慶等[3]表明了數據挖掘能為我們提供有價值的重要信息或知識，從而產生不可估計的經濟效益。李春青[4]認為關聯規則算法是數據挖掘算法中重要的分析方法，能夠挖掘數據中各項關聯。然而，分析從大眾健康檢查收集來的數據集相當困難，因為它們包括許多相關變量，探索高維交易數據內的關聯規則時，數據過于復雜抽象，因而難以被直觀的展示出來。

肖晗等[5]提出通過數據挖掘產生的關聯規則會存在大量無用和不感興趣的規則，同時劉曉蔚[6]提到傳統的類關聯規則挖掘算法在挖掘完整的規則數據集時往往需要消耗很長的時間。此外，Yang[7]提到關聯規則的前提和后果是在所有項的集合的冪集上定義的，并且它們項之間表現出了多對多的關系。而Ferreira等[8]提出可視化技術可以處理大量而復雜的規則。

用于表示大量關聯規則的最常見和簡單的方法是表格。由于其簡單性，基于表格的視圖用于許多常規數據挖掘軟件中，并且這種表格中的規則通常通過諸如置信度或提升的興趣度度量排序。然而，Sekhavat等[9]提出若發現太多關聯規則，分析器在解釋列表和從表中找到有趣的規則仍有困難。

本文介紹了一種稱為結構化關聯圖的新型可視化方法，是關聯規則集合簇熱圖的變體，用于總結高維交易數據中二元變量之間的關系。所提出的方法基于關聯規則挖掘和聚類分析的常規數據挖掘技術，并且其使得用戶能夠容易地找到由一組相關聯的二進制變量形成的感興趣區域，這個區域可構成感興趣的許多關聯規則。由于結構化關聯映射圖是基于矩陣的方法，它很容易實現和解釋。與基于經典矩陣的技術相比，結構化關聯映射圖更適合于解釋給定項集間的多對多關系。

1 研究方法

1.1 挖掘過程

圖1 基于結構化關聯映射圖的關聯規則挖掘過程

圖1描述了基于結構化關聯映射圖的關聯規則挖掘過程，上半部分描述其構建階段，下半部分總結其利用階段。在構建階段，矩陣與以不同方式構造的兩個樹形圖組合，獲得結構化關聯映射圖。創建后，結構化關聯映射圖用于可視化識別感興趣的區域和組，感興趣組由關聯規則挖掘算法探索。

1.2 行項集(因素項)分析

行項集分析的目的是通過對因子項應用層次聚類算法來生成因子項樹形圖。Michael等[10]提出式(1)中的親和度是兩個項集a和b的相似性度量，而式(2)中的Jaccard距離可以用于測量它們之間的距離，其中sup(X)表示項集集合X。在本文中，式(2)中的距離度量用于生成因子項集樹形圖。

(1)

Jd(a,b)=1-A(a,b)

(2)

DF因子項的平方距離矩陣可如式(3)獲得，其中mf是因子項的數量，并且dfij=Jd(Fi，Fj)，Fi和Fj為因子項集。 注意，如果i=j且dfij=dfji，則dfij=0。

(3)

在本文中，凝聚層次聚類算法應用于距離矩陣DF，以生成樹形圖。聚集聚類算法需要確定兩個聚類(項集)之間的距離的鏈接標準。Tan等[11]提出常用的鏈接標準是單鏈(SL)、完全鏈(CL)、平均鏈(AL)和Ward’s標準(WC)。本文通過對比四種標準，找出最優值。而用于對樹形圖的子樹進行排序的方法使用基于支持度量(OM)，這是一個簡單的自上而下排序方法，從最高合并點開始。在每個合并點，此方法查找哪個子樹具有支持最高的項集，并將其放在樹形圖的左側(上側)。

1.3 列項(響應項)分析

通過層次聚類算法獲得響應項DR的距離矩陣，來生成響應項樹形圖。

在本文中，響應項Rj的定義如下：

PF(Rj)=[L1j,L2j,…,Lmj j]

(4)

式中：Lij是Fi對Rj的影響。規則“{Fi}→{Rj}”的興趣度量用Lij表示，并且本文通過使用升力測量來計算Lij如下：

(5)

考慮因子項的影響的分布，Rj和Rk之間的距離drjk計算如下：

(6)

式中：PF(Rj)·PF(Rk)是兩個輪廓向量PF(Rj)和PF(Rk)的內積，|PF(Rj)| 是PF(Rj)的長度。

1.4 結構化關聯映射圖的評價

本文引用一種基于興趣的評估方法，即2×2規則貢獻的和，由“相鄰”項組成的概念。

如下計算2×2規則貢獻的和測量：

(7)

式中：CN({F(i)，F(i + 1)}→{R(j)，R(j + 1)})是{F(i)，F(i + 1)}→{R(j)，R(j + 1)}的規則。 如果先導和后繼項集都連接到縮減的結構化關聯映射圖的樹形圖中，則該規則被關閉，并且其貢獻計算如下：

CN(closedrule)=LIFT(closedrule)

(8)

式 (8)中的CN(closedrule)表示閉合規則應當具有高興趣度值，因此分析器傾向于期望它們是有趣的規則。

如果在縮減結構化關聯映射圖的樹形圖中既沒有連接先導項也沒有連接后繼項，則打開關聯規則，并且如下獲得其貢獻：

CN(openedrule)=

(9)

式(9)中的CN(openedrule)意味著打開的規則具有低興趣度值。因此，打開的規則的貢獻是其升力的倒數，如果它具有正升力值。如果打開規則的提升為0，則規則的貢獻被設置為任意值M，并且本文中M=1。

1.5 結構化關聯映射圖利用率

結構化關聯映射圖用于可視化探索給定事務數據內的二進制變量之間的關系。并且，結構化關聯映射圖通過應用關聯規則挖掘算法幫助用戶更深入地找到要研究的感興趣區域。

設S(a，b，p，q)表示由代表F(a)，F(a + 1)，…，F(a + p-1)的行和代表R(b)、R(b + 1)、R(b + q-1)的列，當p,q≥2時，組成的結構化關聯映射圖的p×q子矩陣。如果滿足以下兩個條件，則將S(a，b，p，q)稱為感興趣區域：

(1)S(a，b，p，q)中的幾乎所有eijs指示F(i)和R(j)之間的正相關，或eijs指示F(i)和R(j)之間的負相關(a≤i≤a+p-1，b≤j≤b+q-1)。

(2)F(a)，F(a + 1)，…，F(a + p-1)在要素項集樹形圖中以較低的級別合并，且R(b)、R(b + 1)、R(b + q-1)在響應項樹形圖中的較低級合并。

如果S(a，b，p，q)是感興趣區域，則與該子矩陣G(a，b，p，q)相關的項集合被稱為感興趣組。

G(a,b,p,q)= {F(a),F(a+1),…,F(a+p-1)}∪

{R(b),R(b+1),…,R(b+q-1)}

(10)

2 應用實例

2.1 大眾健康檢查結果數據集

原始數據從韓國278個青少年的大眾健康檢查收集。其中，兩類變量表示受試者的身體狀況或病史，由專職醫務人員檢查。其他類別中的變量表示主觀癥狀和個人生活方式，基于受試者對感知健康狀況的陳述。圖2為大眾健康檢查結果數據集的項集分類。

圖2 大眾健康檢查結果數據集的項集分類

通過使用結構化關聯映射圖來探尋個人牙齒健康可視化變量之間的關系。本文選擇生活方式變量作為因子項，主觀癥狀和牙科疾病變量作為響應項，分析形式“{Ilife}→{Isymptom∪Idisease}”的關聯規則。

2.2 結 論

一旦項集被分類，下一步是生成因子項集樹形圖。為此，凝聚層次聚類算法應用于因子項的距離矩陣DF，通過使用式(2)獲得。

然后，我們可以通過使用式(4)-式(6)生成響應項，并且這些響應項用于計算響應項DR的距離矩陣。同樣，響應項樹形圖通過應用層次聚類算法獲得。

由于我們有4個因素項集樹狀圖和相同數量的響應項集樹狀圖，可以構造4個不同的結構化關聯映射圖。可以通過使用式(8)-式(10)中描述的2×2規則貢獻的和測量來評價它們的性能，評價結果總結在表1中。在表1中，每行指示因子項集樹形圖的排序方法和鏈接標準，而每一列指定響應項集樹形圖的排序方法和鏈接標準。

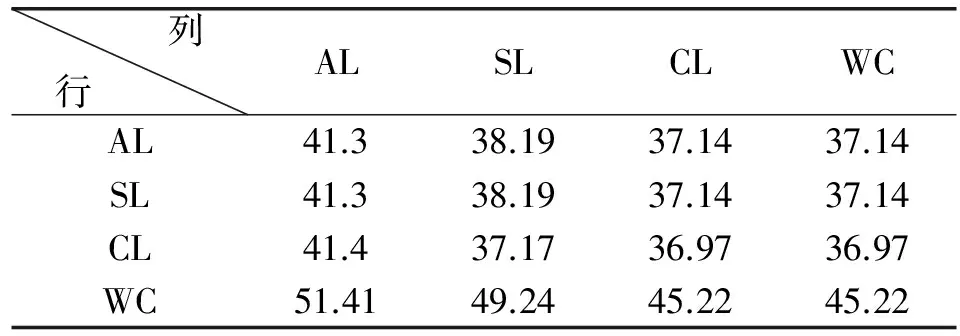
表1 不同結構化關聯映射的2×2規則貢獻的和值

圖3 2×2規則貢獻的和值的分布

圖4 結構化關聯映射圖與最高2×2規則貢獻的和(結構化關聯映射圖與OM-WCOM-AL)

表1的第i行和第j列中的元素表示通過組合第i個因子項集樹形圖和第j個響應項集樹形圖構建的結構化關聯映射圖的2×2規則貢獻的和值，并且可以看出結構化關聯映射圖的性能根據組合樹形圖的結構而顯著變化，如圖3所示。在表1中列出的16個不同的結構化關聯映射圖中，我們必須選擇具有WC/AL的結構化關聯映射圖(因子項集樹形圖結構/響應項集樹狀圖結構)，因為它使2×2規則貢獻的和測量的值最大化。因此，我們可以獲得如圖4所示的優化的結構化關聯映射圖。其中每個方塊eij根據關聯規則“{F(i)}→{R(j)}”的提升值被著色，如下：① 方塊內含三角指示升力值高于1(正相關)，而普通方塊意味著升力值低于1(負相關)。② 較深色的瓷磚表示較強的相關性，無色瓷磚表示升力值約為1(F(i)和R(j)之間的周相關性)。

3 結 語

本文提出了一種稱為結構化關聯映射圖的新型可視化方法，精心設計來表示大型交易數據中項集之間的復雜關系。其與經典簇熱圖相似，因為矩陣與兩個樹形圖組合。然而，結構化關聯映射的樹形圖以更復雜的方式構建，以避免對多對多關聯規則的誤解。優化了之前工作中引入的結構化關聯映射的抽象概念，并開發了構建優化其詳細概念和增強的過程。

[1] Boulware L E,Barnes G J,Wilson R F,et al.Value of the periodic health evaluation[J].Evidence Report/technology Assessment,2006(136):1.

[2] Kweon S,Kim Y,Jang M J,et al.Data resource profile:the Korea National Health and Nutrition Examination Survey (KNHANES)[J].International Journal of Epidemiology,2014,43(1):69-77.

[3] 邊根慶,王月.一種基于矩陣和權重改進的Apriori算法[J].微電子學與計算機,2017,34(1):136-140.

[4] 李春青.基于關聯規則算法的數據挖掘研究[J].軟件導刊,2017,16(2):147-149.

[5] 肖晗,黃誠.基于量化關聯規則的敏感性分析[J].計算機應用,2017,37(S1):1-6.

[6] 劉曉蔚.基于等價類規則樹的高效關聯規則挖掘算法[J].計算機應用與軟件,2015,32(1):313-319.

[7] Yang L.Pruning and visualizing generalized association rules in parallel coordinates[J].IEEE Transactions on Knowledge & Data Engineering,2005,17(1):60-70.

[8] Ferreira d O M C,Levkowitz H.From visual data exploration to visual data mining:a survey[J].Visualization & Computer Graphics IEEE Transactions on,2003,9(3):378-394.

[9] Sekhavat Y A,Hoeber O.Visualizing Association Rules Using Linked Matrix,Graph,and Detail Views[J].International Journal of Intelligence Science,2013,3(1):34-49.

[10] Hahsler M,Buchta C,Gruen B,et al.Mining Association Rules and Frequent Itemsets[EB/OL].2017.https://cran.r-project.org/web/packages/arules/arules.pdf.

[11] Tan P N,Steinbach M,Kumar V.Introduction to Data Mining,(First Edition)[M].Addison-Wesley Longman Publishing Co.Inc.2005.

EXPLORINGSTRUCTUREDASSOCIATIONMAPOFASSOCIATIONRULESVISUALIZATION

Yi Li1Hu Yameng1,2Peng Yanbing1

1(FiberHomeStarrySkyCo.,Ltd.,Nanjing210019,Jiangsu,China)2(WuhanResearchInstituteofPostsandTelecommunications,Wuhan430074,Hubei,China)

The users often face difficulties in interpreting and exploiting the association rules extracted from large transaction data with high dimensionality. There are two main reasons. Firstly, too many association rules can be produced by the conventional association rule mining algorithms, and secondly, some association rules can be partly overlapped. This problem can be solved if the users can select the relevant items to be used in association rule mining. In this context, this paper aims to propose a new visual exploration tool, structured association map, which enables the users to find the group of the relevant items in a visual way. For illustration, this procedure is applied to a mass health examination result data set, and the experiment results demonstrate that structured association map with maximum sums of 2×2 regular contributions value helps to reduce the complexities of association analysis significantly and it enables to focus on the specific region of the search space of association rule mining while avoiding the irrelevant association rules.

Visualization Association rule mining Hierarchical clustering Structured association mapping

2017-05-15。易黎，工程師，主研領域：大數據分析。胡雅萌，碩士生。彭艷兵，教授級高級工程師。

TP391.4

A

10.3969/j.issn.1000-386x.2017.12.013