基于偽隨機陣列和正弦光柵的結構光標定

王靜強 劉桂華 趙碧霞 王玉玫

(西南科技大學特殊環(huán)境機器人技術四川省重點實驗室 四川 綿陽 621010)

基于偽隨機陣列和正弦光柵的結構光標定

王靜強 劉桂華 趙碧霞 王玉玫

(西南科技大學特殊環(huán)境機器人技術四川省重點實驗室 四川 綿陽 621010)

針對投影儀-攝像機結構光系統(tǒng)標定精度低的問題，提出一種基于偽隨機陣列與正弦光柵結合的標定算法。該方法直接對標定板角點進行編碼，根據(jù)角點在不同坐標系下的點對關系求解系統(tǒng)參數(shù)，提高了傳統(tǒng)的編碼精度和結構光系統(tǒng)標定精度。在正弦光柵條紋中心處投射偽隨機陣列，根據(jù)偽隨機陣列窗口的唯一性和相移法可求出正弦光柵的真實相位；分別在水平和豎直方向投射正弦光柵，根據(jù)不同方向的真實相位值形成對標定板角點的唯一編碼；根據(jù)編碼值獲得標定板角點在投影儀像平面、攝像機像平面和世界坐標系下對應點集，根據(jù)相機標定算法可得到投影儀、相機的內(nèi)外參數(shù)。該方法直接對標定板角點高精度編碼，求解世界坐標點和像素坐標點的對應關系，僅需要普通棋盤格標定板可實現(xiàn)高精度標定。實驗結果表明最大反投影殘差為0.7像素，棋盤格角點重建均方差為0.08 mm。

偽隨機陣列 正弦光柵 投影儀標定

0 引 言

在三維測量領域，基于機器視覺的測量技術有著廣泛的應用。光柵和偽隨機碼投影技術是主動光三維視覺主要的編碼方法，具有高精度、高分辨率、非接觸式等優(yōu)點。在視覺引導、工業(yè)測量、逆向工程等方面有著廣闊的研究前景。由單相機-投影儀組成的結構光測量系統(tǒng)，利用投影儀投射圖形可以作為相機成像的逆過程的原理，將投影儀和相機作為兩個約束，滿足三角測量的必備條件。傳統(tǒng)的系統(tǒng)測量需要由投影儀投射偽隨機碼、格雷碼、正弦光柵等編碼圖案，攝像機采集經(jīng)由物體深度信息調(diào)制的變形圖案，根據(jù)圖像中編碼圖案的變化來恢復物體的三維信息。其中系統(tǒng)的結構參數(shù)標定對重建結果影響很大，主要包括相機和投影儀的內(nèi)參數(shù)以及外參數(shù)標定。

高治華提出的投射圓點圖案的標定方法[1]，首先將圓點圖案投射在圓心標定板上，根據(jù)射影變換原理建立投影儀圖像和攝像機圖像的對應關系。這種方法依賴于攝像機標定的精度，而且需要解出投射的圓形圖案和標定板標記點的位置關系，然后才能得到圓形標志點在平板上和投影儀圖像坐標，增加疊加誤差造成標定精度下降。才啟勝等提出的基于神經(jīng)網(wǎng)絡的結構光標定法[2]，該方法雖然簡化了建模的復雜度和提升了適應性，但得到投影儀近似模型且訓練需要數(shù)據(jù)量大、耗時長。唐蘇明等提出基于偽隨機碼標定法將偽隨機碼用在角點編碼中[3-4]，在一定程度上改善了算法，但在求取標記點世界坐標時采用交比不變性，依然有累計誤差。雷震等提出可切換棋盤格與白板的特制標定板來標定結構光系統(tǒng)[5]。在白板上投射網(wǎng)格圖案，利用攝像機的標定結果求取特征點三維坐標，其系統(tǒng)標定精度嚴重依賴于攝像機標定。陸軍等提出了基于格雷碼和線移編碼的結構光系統(tǒng)標定法[6]，該方法將格雷碼應用于標定，減少了棋盤格背景對編碼圖案的影響，提高了精度，但格雷碼編碼與解碼耗時，不利于在線實時標定。Ouellet等提出的標記圓標定法[7]，投射標記圓在標定板上，在攝像機像平面中根據(jù)攝影變換求出標記點三維坐標。該方法使用投射的標記圓在不同坐標系下的坐標點，對結構光系統(tǒng)標定。相比于直接利用標定板的標準圓心在不同坐標系下的坐標的方法，該方法增加了累計誤差且受相機的標定精度影響較大。

本文提出了基于偽隨機陣列和正弦光柵相結合的投影儀-相機標定方法。分別在水平和豎直方向向標定板投射正弦光柵[7-9]和偽隨機碼[10-11]。用偽隨機陣列對投射在標定板上的正弦光柵條紋進行定級，水平和豎直方向的相位真實值對棋盤格角點形成唯一的編碼，根據(jù)編碼值實現(xiàn)世界坐標點和相機坐標點、投影儀坐標點的完全對應。根據(jù)張正友標定法[3]可實現(xiàn)對相機-投影儀的內(nèi)外參數(shù)標定，本文方法直接對標準的標定板角點進行唯一編碼，并使用標定板角點在不同坐標系下的對應關系標定系統(tǒng)參數(shù)，減少了傳統(tǒng)方法中使用投射的標記點進行系統(tǒng)標定時所造成的累積誤差且不依賴于攝像機的標定結果。

1 系統(tǒng)方案

系統(tǒng)的總體方案設計如圖1所示。首先控制投影儀和相機，當投影儀在水平和豎直方向向標定板投射初始相位為0、π/2、π，3π/2的正弦光柵時，雙目相機采集不同相位的圖片。然后投射偽隨機碼陣列，用同樣的方式記錄標定板上的圖案。

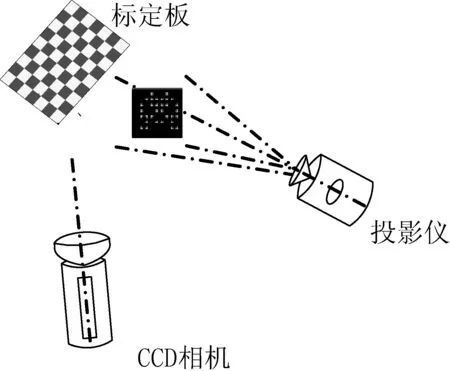
圖1 系統(tǒng)平臺設計

系統(tǒng)流程如圖2所示。根據(jù)相機拍攝的水平和豎直方向正弦光柵和偽隨機碼，可以解得兩個方向的真實相位值，提取棋盤格的角點。根據(jù)角點的像素坐標和水平與豎直方向的相位真實值，實現(xiàn)對棋盤格角點的唯一編碼。在投影儀投射的圖案中，每個像素都有其唯一的編碼，利用編碼值可以求出標定板角點在投影儀坐標系、世界坐標系、相機坐標系下的坐標。根據(jù)張正友標定法求出相機和投影儀的內(nèi)參數(shù)及投影儀和相機之間旋轉(zhuǎn)平移矩陣。

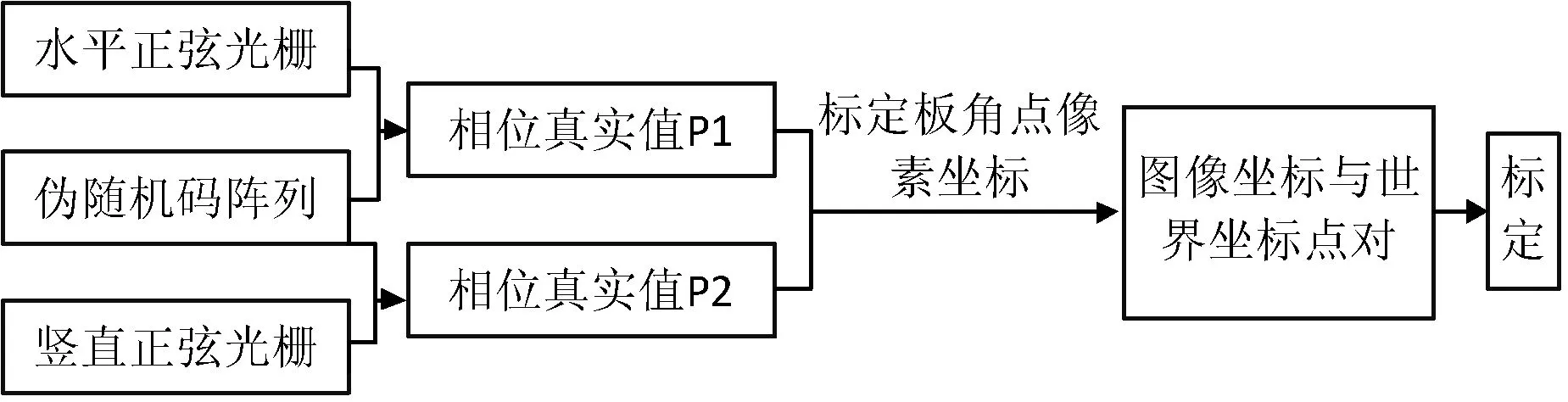
圖2 系統(tǒng)流程圖

2 算法設計

2.1 偽隨機陣列應用

2.1.1 偽隨機碼生成

偽隨機序列由本原多項式式(1)指定的移位寄存器產(chǎn)生。

H(x)=xm+km-1xm-1+…+k2x2+k1x+k0

(1)

選取的移位寄存器有四種狀態(tài)，且令本原多項式系數(shù)GF(q)={0,1,w,w2}，w為本原。移位寄存器可以輸出一個周期為T的偽隨機序列。

T=qm-1

(2)

式中：m為寄存器個數(shù)，q為存儲器狀態(tài)數(shù)。偽隨機序列輸出時需要不斷地更新最左邊移位寄存器的值pa+m。

pa+m=h(pa+m-1,pa+m-2,…,pa)

(3)

本文選取存儲器的狀態(tài)為0和1。構建的偽隨機序列周期為64，偽隨機陣列為7行9列。陣列特性窗口為3行2列，m=6。故本原多項式為h(x)=x6+x+1，反饋移位寄存器如圖3所示。

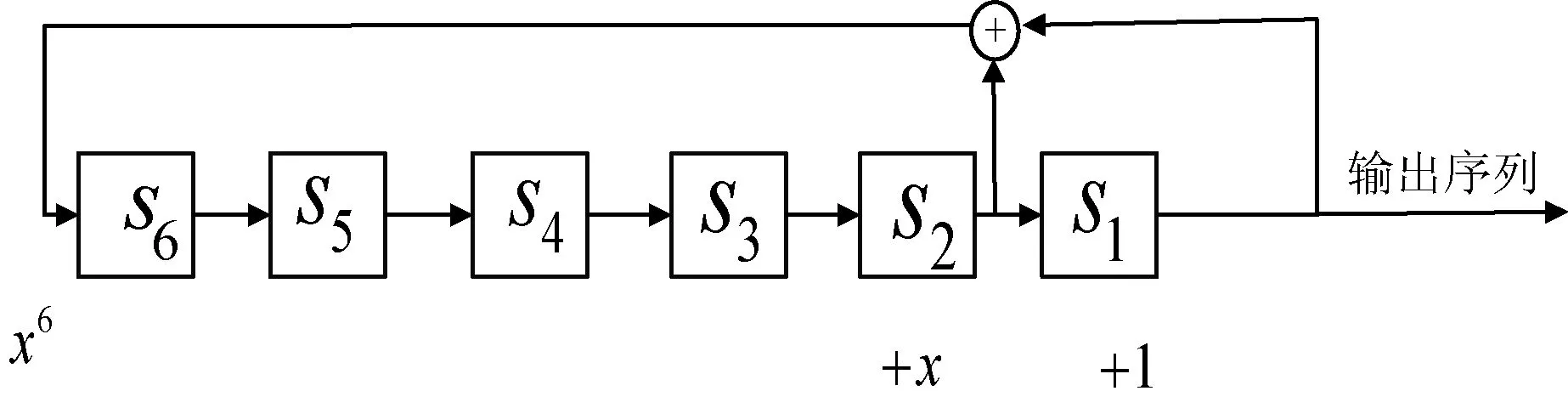
圖3 移位寄存器圖

式中：⊕表示摸2加法。設序列初始值為000001，則生成周期為63的偽隨機序列為：

00000100001100010100111101000111001001011011101

1001101010111111。

2.1.2 偽隨機陣列編碼

偽隨機陣列在指定的窗口大小下具有唯一特性，假設構成偽隨機陣列為A，

(4)

根據(jù)式(4)得到的周期為7行9列的偽隨機陣列如圖4(a)所示。將該陣列應用在標記圓編碼中，得到如圖4(b)所示偽隨機編碼圓。

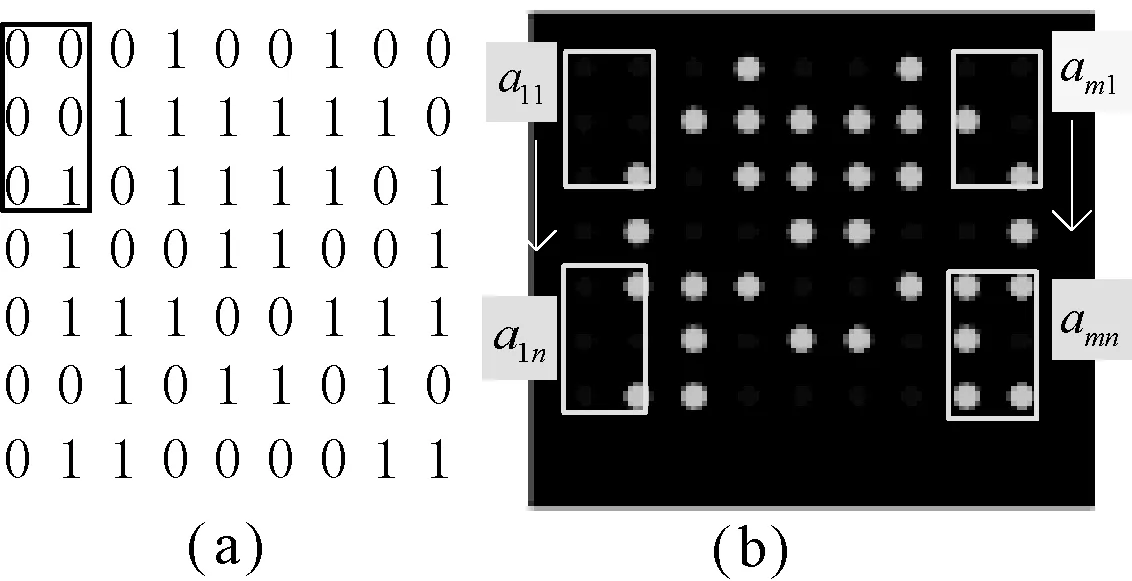
圖4 偽隨機編碼圓圖

2.2 正弦光柵相位解包裹

正弦光柵的解碼包括相位主值的求取和真實相位值的展開兩步[12-13]。在本文采用四步相移法計算包裹相位。由于正弦光柵投射到漫反射物體表面后，CMOS相機獲取的變形柵圖像滿足公式：

F0(x,y)=A(x,y){B(x,y)+C(x,y)cosφ(x,y)}

(5)

式中：A(x,y)表示物體表面的反射率、B(x,y)為背景光強，C(x,y)為條紋幅度，φ(x,y)是初始相位。

根據(jù)式(5)可以得出：

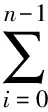
(6)

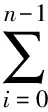
(7)

從式(3)、式(4)中可以計算出n幀相移的相位函數(shù)[7]：

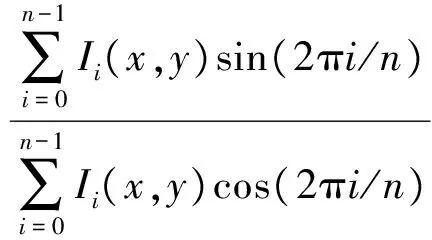
(8)

本文選擇四步相移法，故n=4，根據(jù)式(5)解得相位主值為：

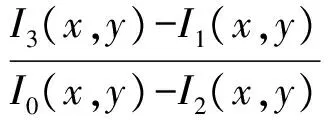
(9)

2.3 正弦光柵相位真實值求取

根據(jù)式(9)得到的正弦光柵的相位主值在[-π,π]，需要求出真實的相位值才能用于棋盤格角點編碼。本文利用偽隨機陣列窗口的唯一特性對正弦光柵條紋進行定級，首先將本原為0和1的偽隨機陣列用紅色和綠色圓表示。如圖4所示，編碼圖案的圓心與正弦光柵的條紋中心一一對應，編碼圓和正弦光柵分別投射于標定板上，根據(jù)透視投影原理，圓心在同一直線上的編碼圓在標定板上的像仍然共線。如圖4所示，3行2列的窗口中，左上角第一個圓心定義為a11，從a11到a1n定義為1級，從am1到amn定義為m級。則條紋級數(shù)q由式(10)求出:

(10)

式中：a為在標定板上提取到的編碼圓陣列中子窗口為3行2列的編碼值。

由攝像機拍攝標定板上的編碼圓圖案，提取圓心并根據(jù)圓心的窗口特性確定圓心所在的級數(shù)。將編碼相同的圓心擬合為直線，該直線在平面標定板上與正弦光柵的條紋中心線重合，因此每條直線的級數(shù)代表正弦光柵的條紋級數(shù)。

由式(9)得到正弦光柵的相位主值φ，由式(10)求出正弦光柵條紋級數(shù)q，將φ和q代入式(11)可以得到相位真實值φ。

φ=φ+2qπ

(11)

2.4 標定板角點編碼與對應點匹配

由于采用水平和豎直方向的光柵投射于棋盤格標定板上，對于棋盤格的每個角點Ci，在水平方向上正弦光柵相位真實值為ph，在豎直方向上正弦光柵相位真實值為pv，在水平和豎直方向上ph和pv的值是唯一的，因此世界坐標系下任意角點Ci的編碼值設為(pv,ph)，如圖5所示。

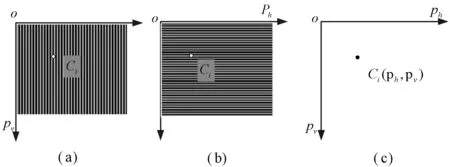
圖5 角點編碼圖

2.5 結構光系統(tǒng)坐標標定

攝像機模型視為理想的小孔成像模型如圖6所示。

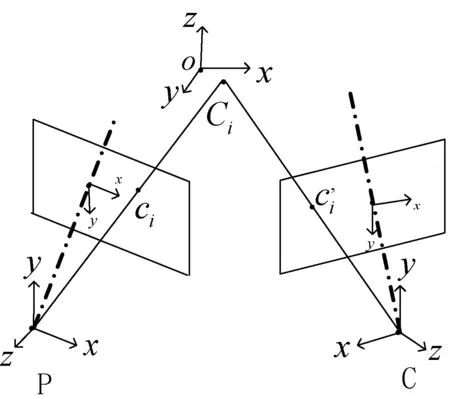
圖6 投影儀模型圖

根據(jù)透視投影原理可得到任意空間點在像平面的對應關系：

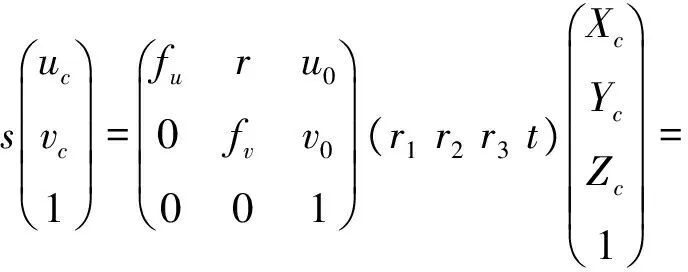
(12)

靶標平面的角點Ci與投影儀像平面對應點ci之間的變換關系為：

sci=(h1h2h3)Ci=HCi

(13)

將點集Si(Ci，ci)代入目標函數(shù)：

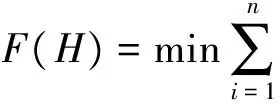
(14)

可求得H，H求出后由旋轉(zhuǎn)矩陣的正交性可得：

(15)

求出A后，每一次標定的外參數(shù)為：

(16)

將世界坐標系下棋盤格角點Ci重投影到投影儀像平面構建目標函數(shù)：

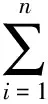
(17)

最小化目標函數(shù)求得在投影儀的內(nèi)參數(shù)和在投影儀坐標系下的外參數(shù)。同理，根據(jù)點集Si(Ci，ci)可求得相機的內(nèi)參數(shù)A′,外參數(shù)R′、T′。設相機坐標系為全局坐標系，需要將投影儀坐標系變換到像機坐標系下，則投影儀透視矩陣為：

H=A[RT]-1R′T′

(18)

根據(jù)三角測量原理,空間中任意一點Ci的三維坐標可由式(10)計算得到：

(19)

式中：H為攝像機透視矩陣，H′為相機透視矩陣。

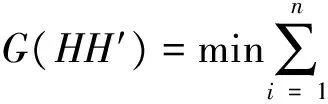
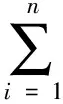
(20)

式中：M為式(10)得出的三角測量方程；P為透視投影方程。最小化目標函數(shù)可得投影儀-相機模型的結構參數(shù)。

3 實驗結果及分析

實驗平臺如圖6所示，采用Inter i7730處理器，三菱MD-565X投影儀分辨率為1 280×1 024，BASLER PIA 2400工業(yè)相機，分辨率為1 280×1 024。

圖7 實驗平臺圖

首先水平和豎直方向的正弦光柵以及偽隨機碼投射于標定板上，為了減小棋盤格角點對編碼造成影響，用一層薄紙覆蓋在標定板表面，如圖8所示。

圖8 光柵和偽隨機碼投影圖

分別在水平和豎直方向上利用四步相移法，求出標定板上正弦光柵的相位主值，將偽隨機編碼圓進行圓心提取并確定圓心編碼值。根據(jù)偽隨機陣列3行2列的窗口特性，由式(10)可以確定每個圓心的所在正弦光柵的條紋等級。將條紋等級相同的圓心擬合為直線，將條紋級數(shù)直線與正弦光柵相位主值結合解得兩個方向的相位主值，如圖8中所示。

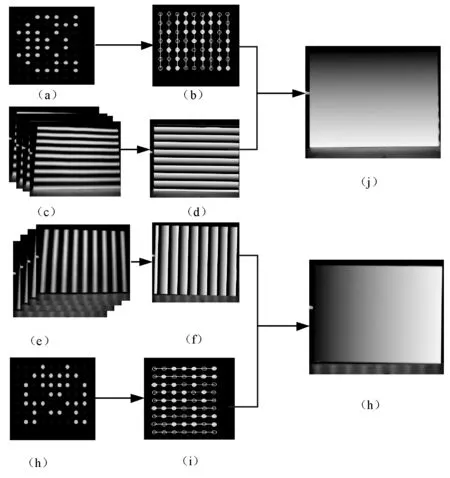
圖9 相位真實值圖

圖9(a)為水平方向偽隨機碼，(b)中偽隨機碼擬合直線代表正弦光柵條紋級數(shù)，(c)為四幅相位初始值相差π/2的正弦光柵，(d)為求得的相位主值，(j)、(h)為根據(jù)相位主值和條紋級數(shù)解得的水平和豎直方向的正弦光柵相位真實值。

根據(jù)水平和豎直方向的相位真實值對棋盤格的角點進行編碼，如圖10所示。

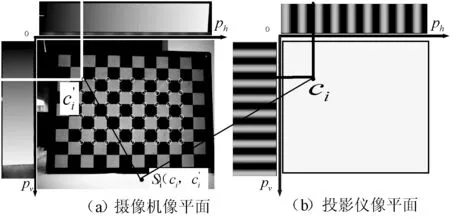
圖10 角點解碼對照圖

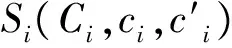
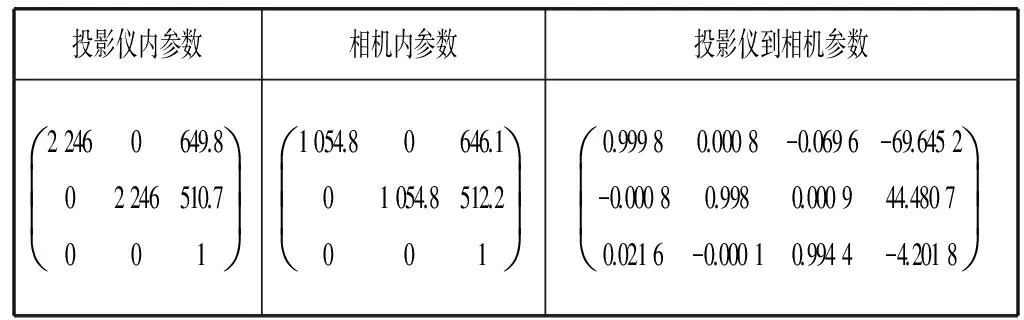
表1 投影儀-相機參數(shù)

為了驗證標定精度，將世界坐標系下棋盤格角點反投影到投影儀像平面，如圖11所示，得到反投影均方差為0.7個像素。

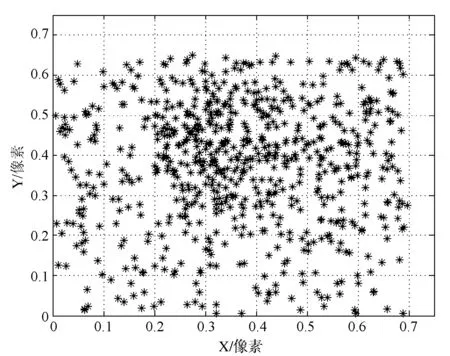
圖11 投影儀反投影殘差圖

將棋盤格角點進行三維重建，得到的角點之間的距離與真實角點之間的距離的做差，根據(jù)不同的標定步數(shù)，得到均方誤差分布，如圖12所示。

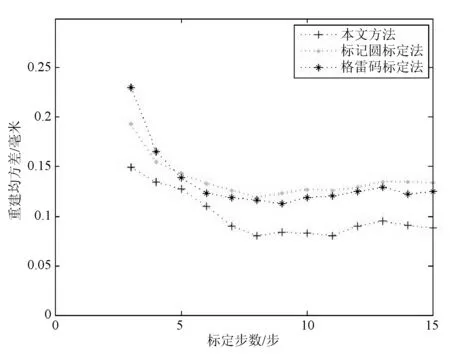
圖12 重建角點誤差圖

由圖11知，8步時可以達到最優(yōu)標定。基于標記圓的標定方法需要在攝像機平面中，求出投射的圓形圖案和標定板標志點的位置關系，根據(jù)射影定理得到圖案在不同坐標系下的坐標。攝像機的精度對系統(tǒng)影響較大。格雷碼標定法采用交比不變性求解投射的格雷碼標志點，采用間接的數(shù)據(jù)對系統(tǒng)進行標定，造成累計誤差較大。本文方法直接對棋盤格角點進行編碼，根據(jù)編碼值直接尋找角點在不同坐標系下對應點集，計算系統(tǒng)的結構參數(shù)，直接用標定板標準角點點集對系統(tǒng)進行標定，消除了使用間接數(shù)據(jù)造成的誤差且不依賴于攝像機標定精度。本文方法與基于標記圓的標定法和格雷碼標定法作對比，本文算法精度可以達到0.08 mm，精度明顯高于標記圓標定法和格雷碼標定法。

4 結 語

針對傳統(tǒng)投影儀-相機結構光系統(tǒng)標定精度低的問題，本文提出了基于偽隨機陣列和正弦光柵相結合的方法。該方法不依賴于相機標定，直接對棋盤格角點進行編碼，不同于傳統(tǒng)標定法中根據(jù)交比不變性得到的不同坐標系下的角點坐標。直接得到用于標定的角點坐標，使反投影均方差減小到0.7個像素，角點重建最大均方誤差為0.08 mm，提高了標定精度。

[1] 高治華, 王昭, 黃軍輝,等. 基于射影變換的結構光測量系統(tǒng)中投影儀標定方法[J]. 中國激光, 2012, 39(10):154-161.

[2] 才啟勝, 相里斌, 方煜,等. 基于神經(jīng)網(wǎng)絡的結構光系統(tǒng)標定[J]. 光子學報, 2016, 45(5):81-86.

[3] Zhang Z. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//The Proceedings of the Seventh IEEE International Conference on Computer Vision. IEEE, 2002:666-673.

[4] 唐蘇明, 張旭, 屠大維. 偽隨機編碼結構光系統(tǒng)的標定[J]. 儀器儀表學報, 2014, 35(6):1354-1362.

[5] 雷震, 劉曉軍, 盧文龍,等. 一種結構光測量技術中的投影儀標定方法[C]//全國光學測試學術交流會,2014.

[6] 陸軍, 宋成業(yè). 基于格雷碼和線移編碼的結構光系統(tǒng)標定[J]. 光電子·激光, 2012(6):1146-1151.

[7] Quellet J N, Rochette F, Hebert P. Geometric calibration of a structured light system using circular control points[C]//The Fourth International Symposium on 3D Data Processing, Visualization, and Transmission, 2008 June 18-20. Atlanta: IEEE Computer Society, 2008:16-18.

[8] 范國鵬, 周莉, 殷明,等. 基于時空轉(zhuǎn)換法的正弦波光柵尺位移測量系統(tǒng)設計[J]. 傳感技術學報, 2015, 28(9):1367-1372.

[9] 昌馳, 朱革, 付敏,等. 基于光場耦合的時柵位移傳感器設計[J]. 傳感器與微系統(tǒng), 2016, 35(2):113-115.

[10] Dong Z, Hu N. A method for the detection of long pseudo-random code DSSS signals based on the processing of delay-multiply (II)-the estimation of the information symbol period and the pseudo-random code sequence[C]//IEEE International Conference on Communication Technology. IEEE, 2008:233-236.

[11] Zhang S N, Zhao H C, Bing W U. LFM Interference Excision Technique in Pseudo-random Code Fuse Based on Fractional Fourier Transform[J]. Acta Armamentarii, 2006, 27(1):32-36.

[12] 尚忠義, 李偉仙, 董明利,等. 基于四步相移光柵投影的三維形貌測量系統(tǒng)[J]. 應用光學, 2015, 36(4):584-589.

[13] 戴美玲, 楊福俊, 何小元. 基于雙頻彩色光柵投影測量不連續(xù)物體三維形貌[J]. 光學精密工程, 2013, 21(1):7-12.

CALIBRATIONOFSTRUCTUREDLIGHTBASEDONPSEUDORANDOMARRAYANDSINEGRATING

Wang Jingqiang Liu Guihua Zhao Bixia Wang Yumei

(SpecialEnvironmentRoboticsLaboratoryofSichuanProvince,SouthwestUniversityofScienceandTechnology，Mianyang621010，Sichuan，China)

Aiming at the low calibration accuracy of projector and camera structured light system, a calibration algorithm based on pseudorandom array and sine grating is proposed. This method directly encodes the corners of the calibration plate and solves the parameters of the system by the relationship between points in different coordinate systems. It improves the traditional coding precision and the calibration precision of structured light system. First, the pseudorandom array was projected at the center of the sine grating fringe, and the true phase of the sine grating was obtained according to the uniqueness of the pseudorandom array window and phase-shifting method. Secondly, sine grating was projected in horizontal and vertical directions respectively. Each corner of the calibration plate would have a unique code according to the true phase value of different direction. Lastly, the corresponding points in camera and projector as well as world coordinate system was obtained by the code value of corners. The projector and camera’s internal parameters as well as external parameters was figured out according to the corresponding points.This method encodes the corners of the calibration plate to solve the correspondence between the world coordinates points and the pixel coordinates point directly. It only needs common checkerboard calibrated plate can realize high precision calibration. The experimental results show the maximum back projection error is 0.7 pixels and the mean square deviation of corners is 0.08 mm.

Pseudorandom array Sine grating Projector calibration

2017-06-04。國家核能開發(fā)科研項目([2016]1295)；校創(chuàng)新團隊建設基金項目(14TDTK01)。王靜強，碩士生，主研領域：圖像處理及計算機視覺。劉桂華，教授。趙碧霞，碩士生。王玉玫，碩士生。

TP391

A

10.3969/j.issn.1000-386x.2017.12.022