基于數據場的數據勢能競爭與K-means融合的聚類算法
許家楠 張桂珠
(江南大學物聯網工程學院 江蘇 無錫 214122)
基于數據場的數據勢能競爭與K-means融合的聚類算法
許家楠 張桂珠
(江南大學物聯網工程學院 江蘇 無錫 214122)
K-means算法采用歐氏距離進行數據點的劃分,不能夠準確地刻畫數據集特征,而隨機選取聚類中心點的機制,也不能獲得好的聚類結果。為此,提出一種基于數據場的數據勢能競爭與K-means算法融合的聚類算法。算法中定義了數據場的概念,利用局部最小距離進行數據聚合勢能的競爭,然后利用勢能熵提取基于數據集分布的最優截斷距離,根據截斷距離與斜率確定出簇中心點,實現K-means聚類。在UCI數據集上的測試結果表明,融合后的算法具有更好的聚類結果。
數據競爭 數據場 勢能熵 斜率 復雜數據集
0 引 言
聚類分析又稱為聚類,是數據挖掘研究的一個重要方向,是一種將數據對象劃分為不同子簇的過程。每個子簇稱為一類,使得同一類簇的對象差異盡可能小,而不同子簇間的差異盡可能的大[1]。聚類中的方法主要可以分為劃分方法、層次方法、基于密度的方法、基于網格的方法和基于模型的方法。劃分方法中比較典型的有K-means[2]和K-medoids[3]等聚類方法;層次方法中有CURE[4]和CHAMELEON[5]等聚類方法;基于密度的方法中有DBSCAN[6]和OPTICS[7]等聚類方法;基于網格的方法中有STING[8]和WAVECLUSTER[9]等聚類方法;以及基于模型的統計學聚類方法和神經網絡聚類方法。其中K-means算法作為數據挖掘技術中基于劃分方法的一個經典算法,該算法具有理論可靠、算法簡單、收斂速度快而應用廣泛[10]。但是K-means算法存在諸多缺陷:聚類中心點的隨機選取,將導致算法陷入局部最優值;歐氏距離測度,不能夠準確描述數據集的分布信息,難以處理復雜結構的數據集。鑒于以上問題,有Lu等提出一種數據競爭(DC)的聚類算法,通過數據樣本點之間淘汰競爭找聚類中心點完成聚類[11]。DC算法對離群點與噪聲點不是很敏感,具有簡單高效的特點。
DC算法與大多數基于中心的算法一樣,對于球狀簇有很好的處理效果,但是難以處理非球狀以及多維尺度的數據簇,例如密度分布不均勻的數據集。DC算法是在數據相似性矩陣的基礎上進行聚類,而相似性矩陣采用歐氏距離測度,亦不能夠有效地描述數據集數據點之間的相互關系,處理復雜結構的數據集的能力不足。故針對DC算法的缺陷,一種對密度敏感的DC算法被提出,此算法對具有密度流行結構的數據集有較好的聚類效果,但是仍無法處理密度分布不均的數據集[12]。而Zelnik-Manor等提出的基于Self-Tuning相似度的自調節譜聚類算法[13],能夠有效地處理密度分布不均勻的數據集,但Self-Tuning難以應用到類似DC以及K-means這種沒有拉譜拉斯譜映射過程的聚類算法。對于上述算法存在的問題,本文提出了一種基于數據場數據勢能競爭的K-means算法(K-means Algorithm For Data Potential Energy Competition),簡稱K-DPEC算法。該算法根據數據場中簇中心點與同簇數據集中數據點之間相互吸引作用,不同簇聚類中心點相互排斥,且數據場中的簇中心點聚合了該簇中所有點的勢能量,即具有最大聚合能量的點被視為聚中心點。其次,根據數據的分布情況,采用勢能熵確定數據集的最優截斷距離以及結合斜率的想法選出簇中心點。最后利用K-means算法迭代劃分數據點實現聚類。通過仿真實驗表明,K-DPEC算法比原有的DC算法以及K-means算法具有更好的效果。
1 數據勢能競爭(DPEC)聚類算法
1.1 數據場
定義1數據集中內部數據點之間存在類似引力場的作用,使得數據集被吸引力及斥力分裂成不同的簇,而這樣的相互作用稱為數據場。
定義2數據場模型的目的是為了實現描述數據集中簇內數據點與簇中心點之間的關系,按照數據場的概念建立起來的。
Wang等提出數據場來描述數據空間中對象之間的相互作用[14]。在數據場中,數據集內簇中點與屬于該簇的數據點之間存在相互吸引作用,而不同的簇中心點之間存在排斥,并且相同簇內的數據點只會與簇中心點產生作用而不會與簇外數據點發生作用。在物理場中,每個數據對象都被視為一個粒子,勢能被證明存在,且廣泛應用于數據挖掘的任務中[15]。數據對象的勢能可以反應數據空間中數據點的分布,若使用相同的參數,在高密度區域的數據點具有高的勢能,而稀疏區域則具有較低的勢能[16]。許多基于數據場的算法被開發出來,運用在各個領域。為了計算勢能,一定要用到勢能函數。計算勢能的函數有很多,例如:高斯核、指數核、截斷核以及重力核,這里采用高斯核函數。在數據場中,數據簇中心點聚合了數據簇中所有勢能,具有勢能最大值。
數據點xi與數據點xj之間的作用力,使用勢能函數:
(1)
式中:σ是影響因子,對最終的勢能分布有影響,根據此公式,可以計算出勢能矩陣P。
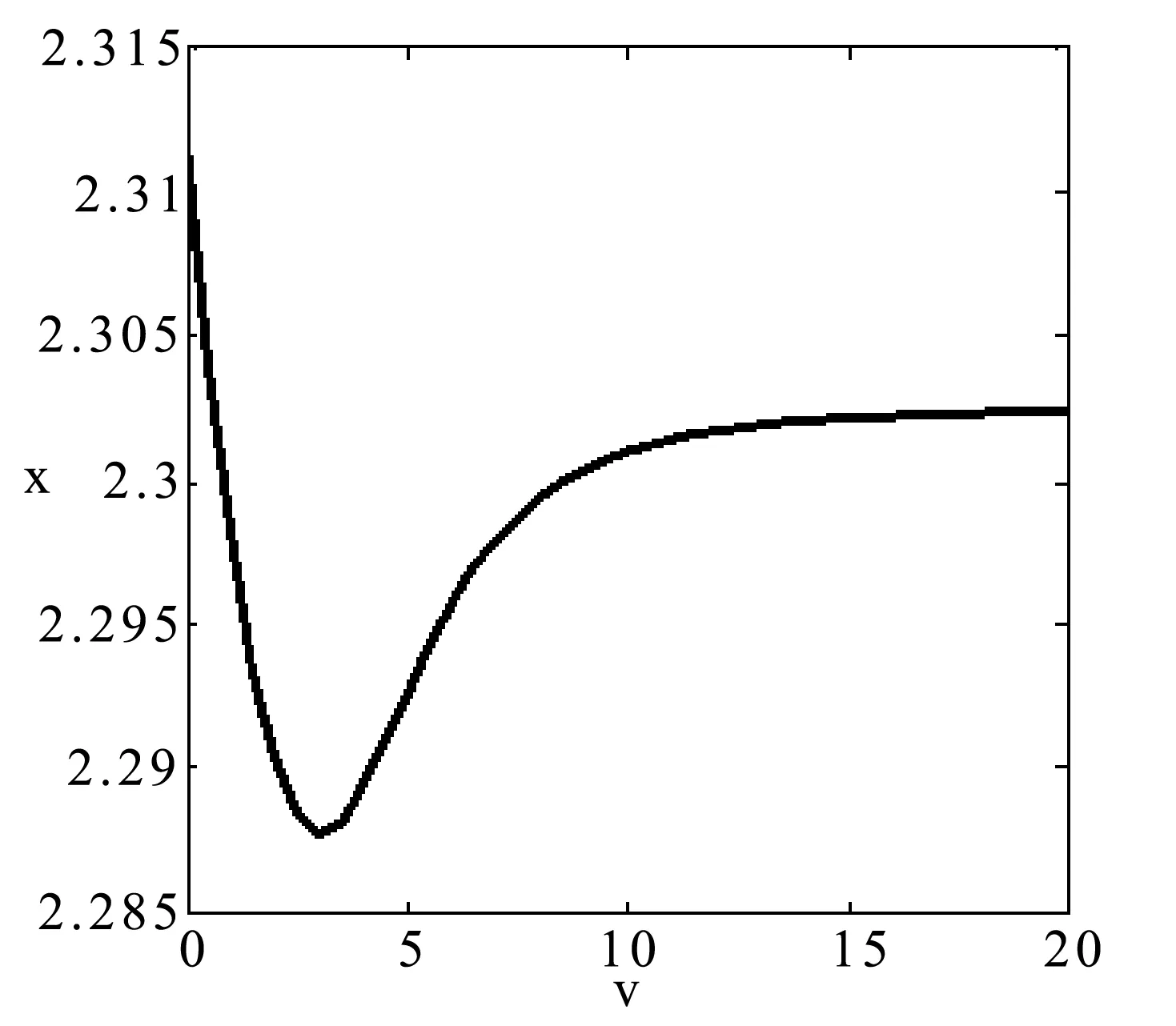
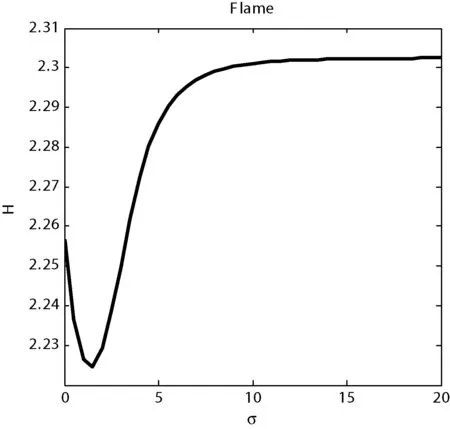
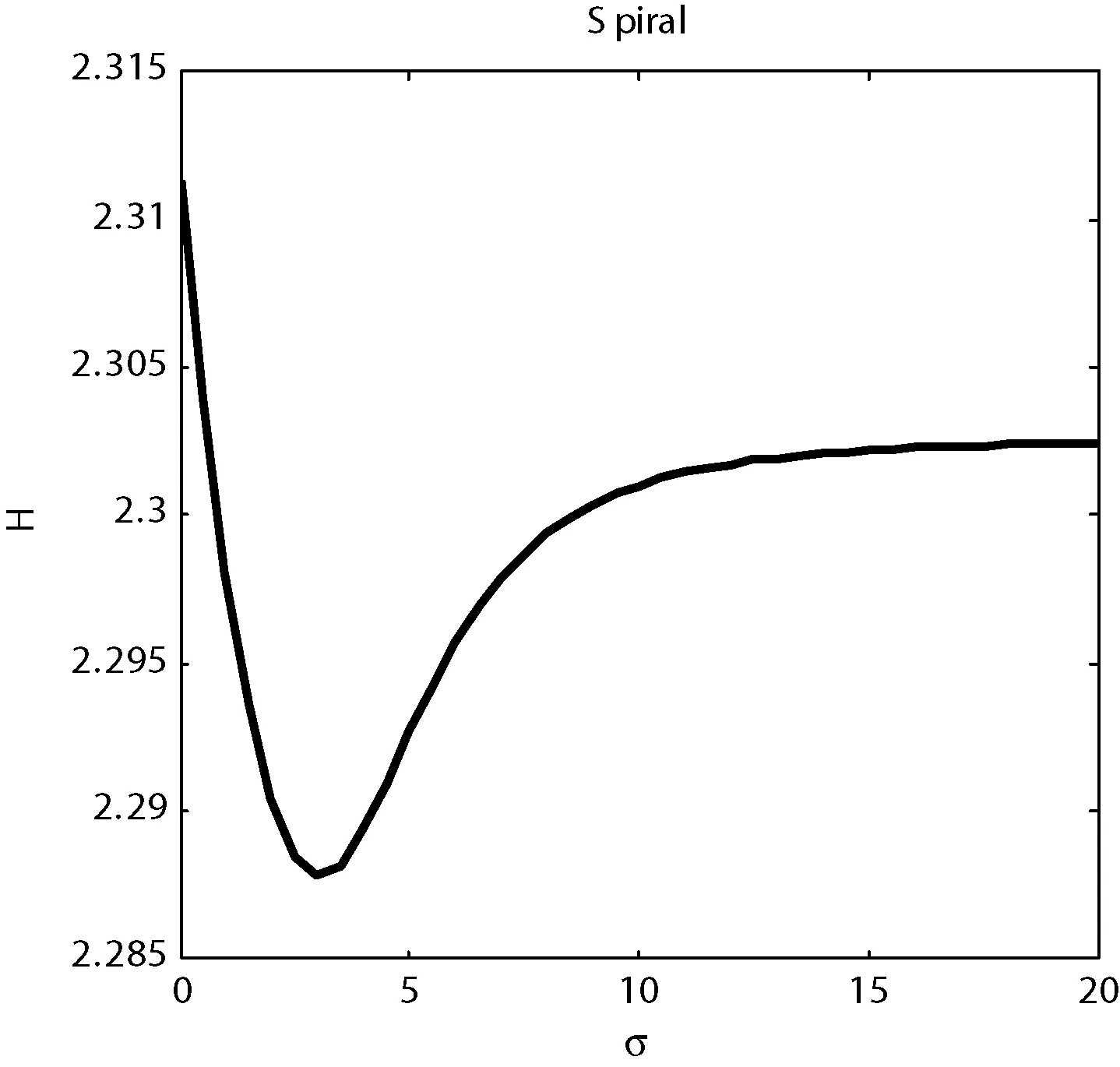
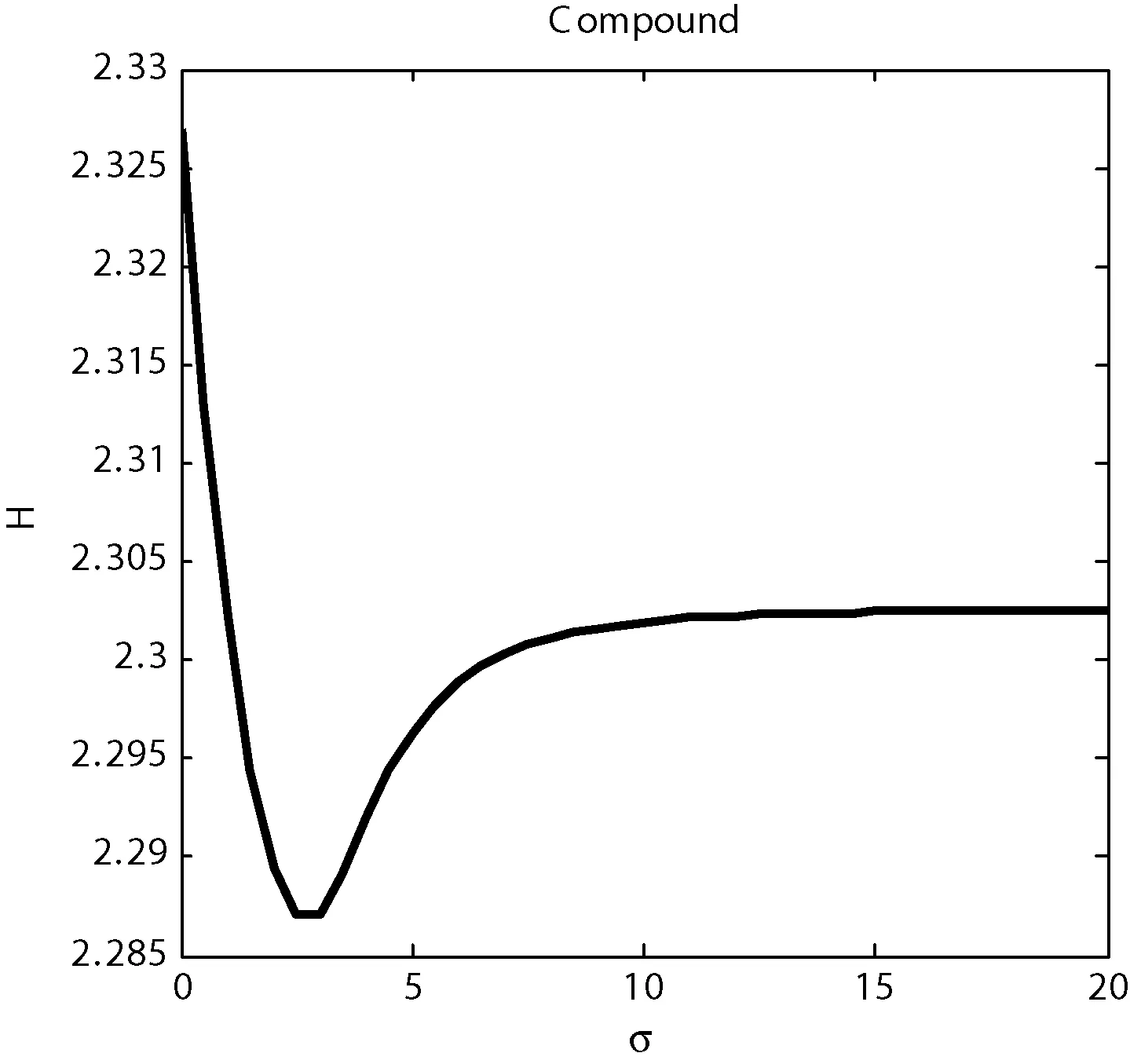
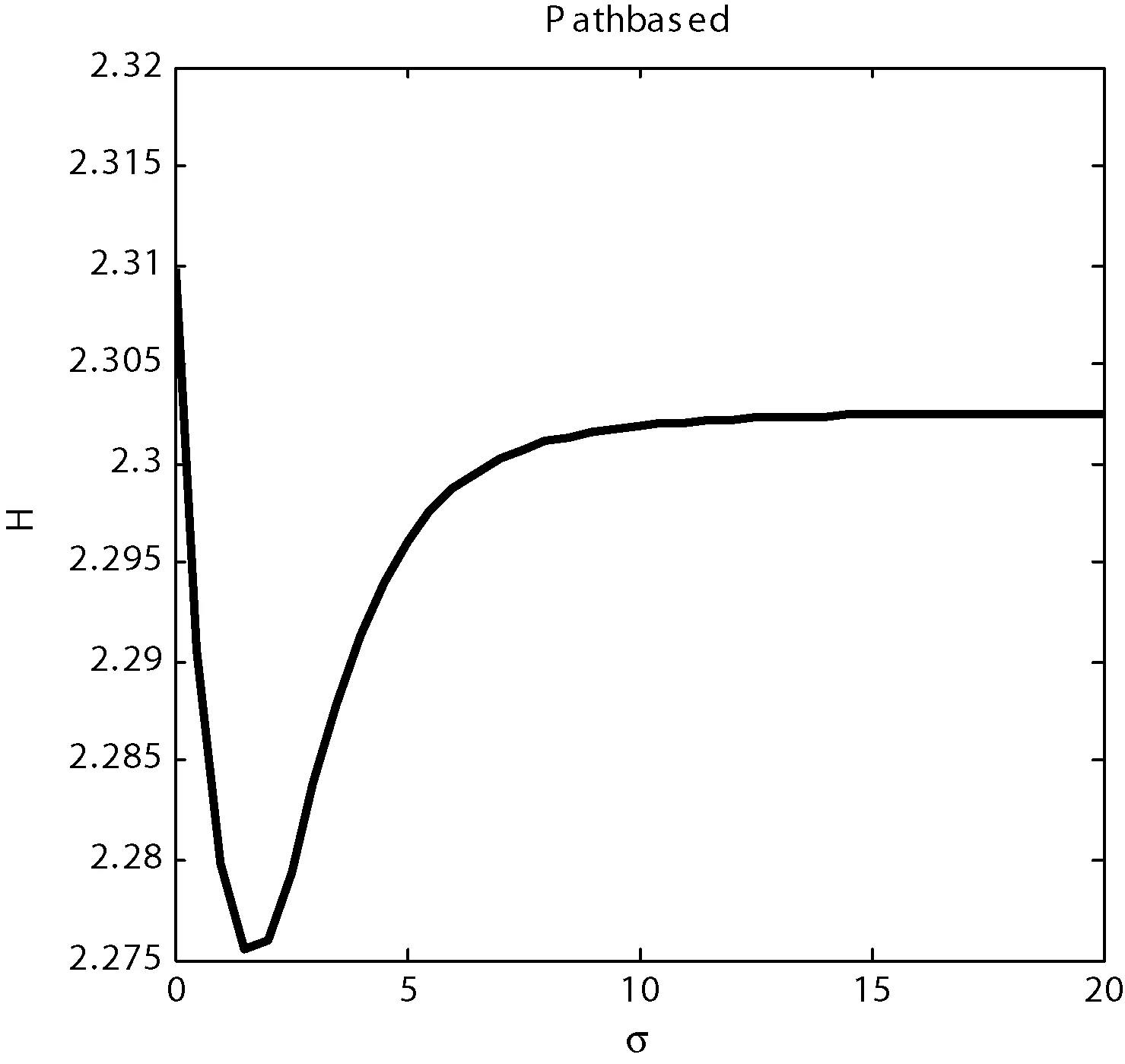
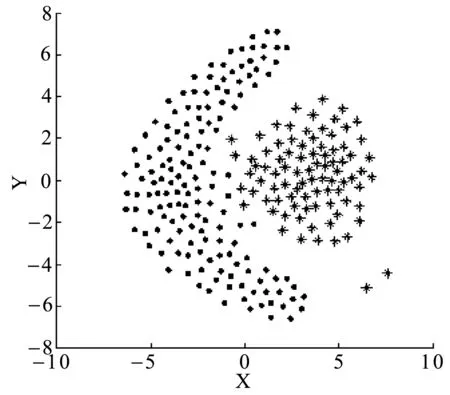
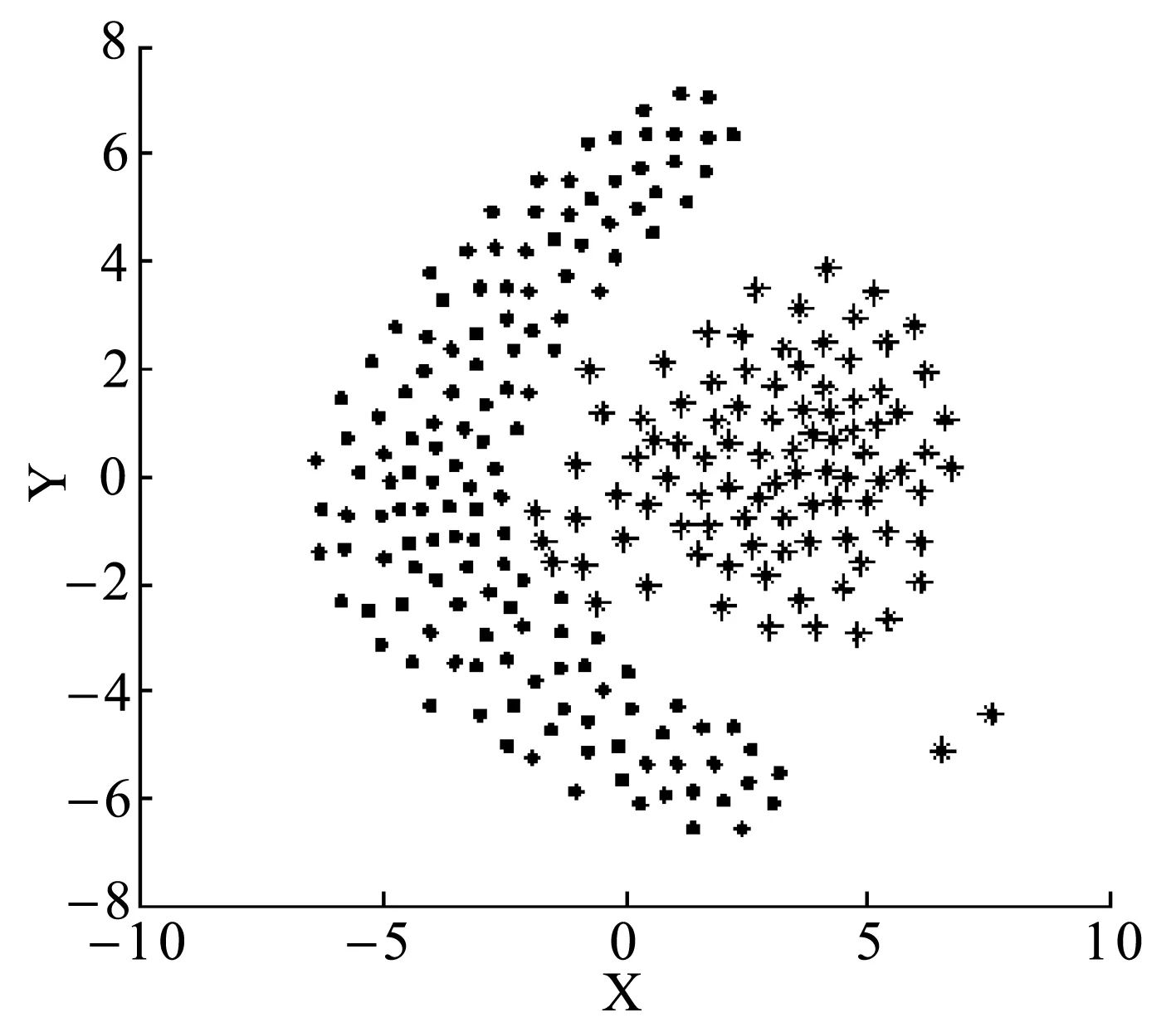
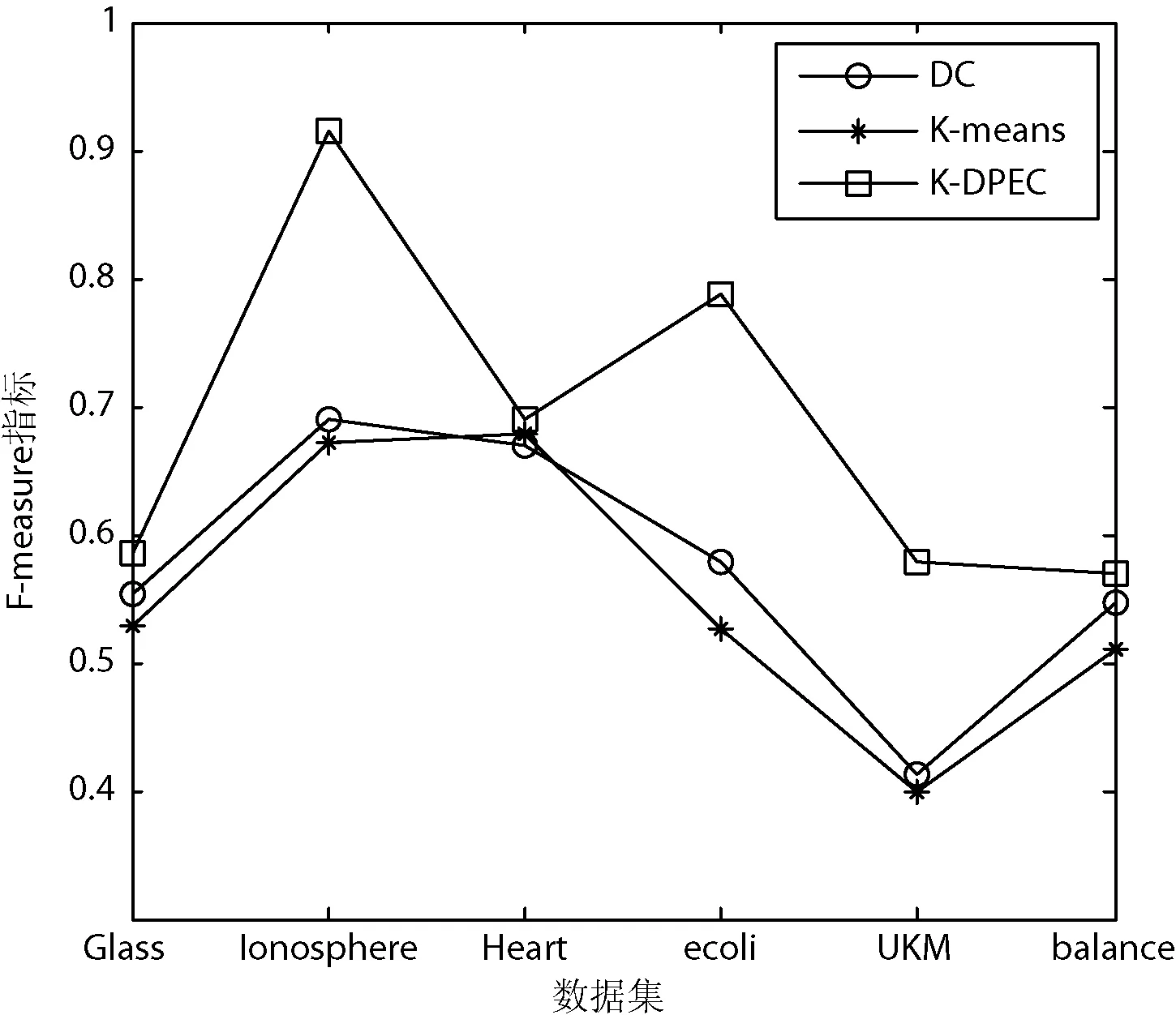
定義3距離數據點xi的最近的r個數據點稱為其鄰近點,則xi的聚合能量Ei為鄰近點與它的勢能總和。1 (2) 原DC算法采用歐氏距離計算兩點間相似度,并定義相似度矩陣,數據點的聚合能量則是其近鄰點的相似度總和。 1.2 基于數據場的聚類 從數據場的概念中可以看出,具有低勢能的數據點相比于高勢能的數據點更有成為簇成員的可能性。在數據場模型中,如果想要成為簇中心點的數據,則這些數據點必須具有足夠遠的距離。若存在數據點之間離得很近的情況,則會有兩種情況,其中一個數據點成為簇成員點,或者兩者都成為簇成員點。在這些數據點中,必須通過淘汰選擇的方式競爭出更有可能稱為簇成員的那個點,從數據集中決出非簇中心點。這種淘汰競爭的方式稱為數據競爭。 存在數據集X={x1,x2,…,xn},其中含有K個簇,n個數據點,dij為數據點之間的距離,D為數據集的距離矩陣。通過局部最小距離(LMD)選出參與數據競爭的數據點對。通過對距離矩陣D進行升序排序,得到首列為0的矩陣D′,如下所示: (3) 若xz是數據集X中存在的唯一離群點,且第一輪的數據競爭次數為n,所以第一輪第n次競爭勢必要為xz與其他某個非離群點的競爭,同時定會將xz標為數據簇的成員點,這也是采用局部最小距離方法的優點之一。采用局部最小距離,可以有效地阻止離群點成為數據簇的中心點,即對離群點不敏感。 當數據簇中的成員點的數目到達n-K時,到達數據競爭的結束條件。而剩下的K個數據點,則為聚類中心點。 聚類是一種無監督的學習,而不同的數據集分布、數據集的結構以及數據集的維度都是不同。基于數據集的這些特點,可以提取其攜帶的先驗信息,利用這些信息可以提高聚類的效果。 DPEC算法通過數據勢能競爭選出具有最大聚合能量的K個點,這些點只能作為最有可能的簇中心點。而算法存在一些問題,對密度分布不均勻的數據結構很難識別。密度分布不均勻的數據結構指的是數據結構中存在一些簇,這些簇的密度與其他簇具有明顯的差別。數據結構密度不均勻分布將導致數據場勢能分布不均勻,因此數據場中則會出現多個具有高勢能的峰值點,這些點也就是具有高聚合能量的點。數據結構中密度的分布不均勻,將導致數據場中同一個區域出現多個峰值勢能點,即可能出現如下情況: (1) 除了明顯的高勢能點,一些具有較低勢能但是具有相對較遠的距離的點都有可能是簇中心點,這些點很容易被忽略。采用數據勢能競爭只考慮到了聚合能量最大的點,將導致簇中心點的錯誤選取。 (2) 若數據場中的同一區域中出現多個勢能峰值點,即具有最大聚合能量的K個點中,有多個出現在同一簇中,則將導致一個簇被錯誤劃分為多個簇的情況。 當數據結構中存在較多簇,或者需要選取多個聚類中心點時,比較容易出現上述錯選的情況。由此可以看出,DPEC算法同樣存在缺陷,雖對離群點不是很敏感,但是對聚類中心點比較敏感,容易出現錯選的情況。針對不同的數據集,尤其是復雜的數據集。因此有必要描述數據集自身攜帶的信息,考慮數據集的分布特點,也就是從全局特征來考慮。針對數據集存在的這些問題,可以設置一個最優截斷距離,同時不同的數據集對應著不同的截斷距離,將在下面說明如何選取。 3.1 最優截斷距離 為了克服DPEC算法對密度分布不均勻的復雜數據集難以識別的缺陷以及簇中心點錯選的情況,可以設置一個截斷距離。為了能夠適應更多更復雜的數據結構,截斷距離的設置有必要具有靈活性,也就是不同的數據結構對應著不同的截斷距離。 對于不同的數據結構,僅僅憑人為經驗來選取是不可取的,截斷距離的選取對最終的聚類結果影響很大。相同的數據集,如果由不同的用戶根據經驗估計,聚類結果可能是不同的。對于不同的數據集,相同的用戶可以評估出不同的截斷距離。為了能夠客觀地選取出最優的截斷距離,通過使用數據場的勢能熵從原始數據集中自動提取截斷距離的最優值的方法。數據集中密度的分布可以用勢能分布來表示,同樣通過密度計算截斷距離方式可以轉為使用數據場中勢能函數的影響因子σ來確定。 在高密度的區域存在高勢能,低密度的區域存在低勢能。根據數據場的原理,若勢能分布不均勻,則不確定性最小[15]。而數據的不確定性通常可以用熵來表示,因此,本文使用熵來優化影響因子σ。 對于數據集X={x1,x2,…,xn},計算每個點的勢能{p1,p2,…,pn},這里使用式(1)計算可以得到,即勢能矩陣中已計算。熵的計算公式為: (4) 式中:Z=∑pi為歸一化因子。 當σ從0增長到∞的時候,熵的值首先迅速下降,然后緩慢增加,最后保持穩定。當熵達到最小時,此時的σ為最優值,如圖1所示。 圖1 最優截斷距離的選取 3.2 簇中心點的優化 由于復雜結構的數據集的密度分布不均勻,導致DPEC算法選出具有最大聚合能量的K個簇中心點可能不具有代表性,有必要對選出的簇中心點進行再次優化以及重新選擇。 通過進行數據勢能的競爭,將數據點根據勢能大小將高能量點放在前面形成降序隊列,會發現競爭后的勢能點會出現兩級分化,具有高勢能的點與絕大多數低勢能點之間存在一個臨界點。將臨界點前的勢能點視為潛在簇中心點,而這些潛在簇中心點的數量勢必大于K,所以有必要確定臨界點。臨界點的定義如下: g=max{i|||ki|-|ki+1||≥λ,i=1,2,…,n-2} (5) λ=α(j)/n-2 (6) (7) 式中:ki表示第i個數據點與第i+1個數據點之間的斜率;α(j)表示P′中相鄰兩點間斜率差的總和;λ表示P′中相鄰點的斜率差的平均值,當數據點間的斜率大于等于λ的所有點中,p值最小的點為臨界點。潛在簇中心點定義如下: 定義6潛在簇中心 pc={i|p′≥p′g,i=1,2,…,g} (8) 將臨界點前的潛在簇中心點進行篩選,將具有最大聚合能量的潛在簇中心點視為默認實際簇中心點。將默認的實際簇中心點,找出與實際簇中心點i最近距離的潛在聚類中心點j,計算兩個點的距離MinDist(i,j)。若MinDist(i,j)>dc,則將點j視為新的實際簇中心點;若MinDist(i,j) 定義7準則函數 (9) 4.1 K-means算法 K-means算法是屬于劃分方法中基于數據相似性度量的間接聚類算法,又稱K-均值算法。該算法將數據集X中的數據劃分為k個簇,劃分的同時采用準則函數來評估聚類的質量,目的是使得簇內數據對象具有高相似度,簇間數據對象具有低相似度。算法步驟如下: 輸入: ?k:簇的數目 ?X:包含n個對象的數據集 輸出:k個簇 步驟: (1) 從X中隨機選擇k個數據對象作為初始簇中心點; (2) Repeat; (3) 根據簇中對象的均值,將每個數據對分配到最相似的簇; (4) 更新簇均值,即重新計算每個簇中對象的均值; (5) Until不再發生變化。 4.2 K-DPEC算法思想 為了增強K-means算法準確選取聚類中心點以及處理復雜數據集的能力,提出了一種數據勢能競爭的K-means(K-DPEC)聚類算法。算法是這樣考慮的:將數據競爭(DC)算法進行了改進與優化,引入了數據場的概念,利用數據點的勢能競爭出簇中心點,提出了一種DPEC算法。同時,DPEC仍然存在缺陷,為了進一步準確選取簇中心點以及處理復雜數據集,采用勢能熵提取了數據集的截斷距離。因截斷距離的選取是從數據集的全局考慮,利用了數據集的先驗信息,同時結合臨界點的定義準確地選取出了簇中心點。最后將簇中心點作為K-means算法的初始簇中心點,將剩余的數據成員進行了數據劃分,直到準則函數的值不再發生變化,結束聚類。 算法步驟如下: 輸入:數據集X={x1,x2,…,xn},簇的數目k 輸出:k個簇C={c1,c2,…,ck} 步驟1利用勢能熵確定影響因子σ并計算截斷距離dc。 步驟2計算數據集的歐氏距離矩陣,根據式(1)計算數據點任意兩點之間的作用力,得到勢能矩陣。 步驟3根據勢能矩陣利用式(2)計算出各數據點的聚合勢能。 步驟4依次選取兩個數據點,利用局部最小距離法進行競爭,將聚合能量最大的點放在隊列隊首,形成降序隊列。 步驟5根據隊列數據點的勢能分布特征,利用式(5)計算斜率并確定臨界點,臨界點前的點視為潛在簇中心點。 步驟6根據截斷距離,篩選出實際簇中心點。 步驟7使用K-means算法將步驟6得到的簇中心點設為初始簇中心點,將其余非簇中心點迭代劃分,并重新計算各類簇的簇中心點以及聚類誤差平方和。 步驟8利用新的簇中心點重新聚類,計算聚類誤差平方和。 步驟9當準則函數的值不再發生變化,結束聚類。否則,重復進行。 為了驗證K-DPEC算法的性能,實驗數據集使用人工數據集與UCI數據集分別進行仿真實驗。實驗環境:Matlab R2013a開發,處理器Intel(R) Core(TM) i7-4710MQ,主頻2.50 GHz,內存8 GB,操作系統為Windows8 64位。 5.1 人工數據集 K-DPEC算法利用勢能熵進行最優截斷距離的選取,實驗中使用Flame、Spiral、Jain、Compound以及Pathbase人工數據集進行展示,數據集描述如表1所示。 表1 人工數據集描述 K-DPEC算法通過對人工數據集提取最優影響因子σ,如圖2-圖6所示,參數設置如表2所示。 圖2 Flame數據集最優σ選取 圖3 Spiral數據集最優σ選取 圖4 Jain數據集最優σ選取 圖5 Compound數據集最優σ選取 圖6 Pathbased數據集最優σ選取 數據集影響因子σ熵值H截斷距離dcFlame1.499012.227851.9294Spiral2.998902.287802.5971Jain1.001402.259500.8672Compound2.497802.287102.1632Pathbased1.389972.275111.2037 為了直觀地顯示算法在人工數據集上的效果,給出了在Flame數據集上的聚類效果。 從圖7至圖9,展示了DC算法、K-means算法以及K-DPEC算法在數據集Flame上的聚類效果。從圖7可以看出DC算法的聚類效果要好于圖8中K-means算法的聚類效果,而圖9中K-DPEC算法又優于DC算法的聚類效果,主要表現在兩簇交界處,這取決于截斷距離選取的優劣。K-DPEC算法通過對數據集的分布情況,利用勢能熵提取出最優截斷距離,對處理非球狀簇等復雜數據集具有很好的效果。 圖7 DC算法在Flame數據集的聚類效果 圖8 K-means算法在Flame數據集的聚類效果 圖9 K-DPEC算法在Flame數據集的聚類效果 5.2 UCI數據集 UCI數據庫為加州大學歐文分校提出的用于機器學習的數據庫,數據庫中的數據集被用來測試機器學習以及數據挖掘算法,且數據庫中的數據集都有確切的分類。UCI數據集描述如表3所示。 表3 UCI數據集描述 為了對聚類結果進行評價,實驗采用常見的F-measure指標評價方法。 F-measure指標是通過算法的準確率(Precision)與召回率(Recall)得到。類i與簇Ck的準確率與召回率如下: 式中:Nik代表類簇k中類別為i的數量;Nk代表類簇k中的樣本的數量;Ni代表類別為i的樣本數量。 F-measure計算公式如下: 式中:α為參數,此公式為準確率(Precision)與召回率(Recall)的加權調和平均。 當α=1時,則為評價聚類結果最常用的F1,公式如下: 數據集整體聚類劃分的F-measure的值則為: 式中:T為數據集真實的類簇集合,N為數據集中樣本數據的總數,C為算法聚類后得到的類簇集合,F-measure指標數值越大,則表示算法聚類越準確。 圖10給了DC算法、K-means算法以及K-DPEC算法的三種聚類算法在UCI機器學習數據集上聚類結果的F-measure指標。 圖 10 圖10展示了3種算法在6個UCI數據集上的F-measure指標的對比。從圖中可以看出K-DEPC算法在UCI數據集上的F-measure指標均好于DC算法與K-means算法,特別是在ionosphere數據集與ecoli數據集上的F-measure指標,得到了大幅的提升。 本文算法針對K-means算法隨機選取簇中心點及難以處理復雜數據結構等弊端,提出了一種基于數據場的數據勢能競爭與K-means算法融合的K-DPEC聚類算法。在K-means算法的基礎上引入改進后的DC算法,利用勢能代替原DC算法的相似度計算,并且引入勢能熵的概念以及斜率的思想,在處理復雜結構數據集和確定聚類中心點上具有較強的能力。通過仿真實驗,在人工數據集以及UCI數據集上的實驗結果,證明了本文算法的可行性。 [1] Xu R,Wunsch D.Survey of clustering algorithms[J].Neural Networks,IEEE Transactionson,2005,16(3):645-678. [2] Jain A K.Data clustering:50 years beyond K-means[J].Pattern recognition letters,2010,31(8):651-666. [3] Park H S,Jun C H.A simple and fast algorithm for K-medoids clustering[J].Expert Systems with Applications,2009,36(2):3336-3341. [4] Zhou Y J,Xu C,Li J G.Unsupervised anomaly detection method based on improved CURE clustering algorithm[J].Journal on Communications,2010,31:18-23. [5] Karypis G,Han E H,Kumar V.Chameleon:Hierarchical clustering using dynamic modeling[J].Computer,1999,32(8):68-75. [6] Jing Yang,Gao Jiawei,Liang Jiye.An Improved DBSCAN Clustering Algorithm Based on Data Field[J].Journal of Frontiers of Computer Science and Technology,2012,6(10):903-911. [7] Kalita H K,Bhattacharya D K,Kar A.A New Algorithm for Ordering of Points to Identify Clustering Structure Based on Perimeter of Triangle:OPTICS(BOPT)[C]//International Conference on Advanced Computing and Communications.IEEE,2007:523-528. [8] Ansari S,Chetlur S,Prabhu S.An Overview of Clustering Analysis Techniques used in Data Miniing[J].International Journal of Emerging Technology and Advanced Engineering,2013,3(12):284-286. [9] Amini A,Wah T Y,Saybani M R.A study of density-gridbased clustering algorithms on data streams[C]//Fuzzy Systems and Knowledge Discovery(FSKD),2011 Eighth International Conference on.IEEE,2011,3:1652-1656. [10] 施培蓓.數據挖掘技術中聚類算法的研究[D].江南大學,2008. [11] Lu Zhimao,Zhang Qi.Clustering by data competition[J].Science China Information Sciences,2013,56(1):1-13. [12] 蘇輝,葛洪偉,張歡慶.密度敏感的數據競爭聚類算法[J].計算機應用,2015,35(2):444-447. [13] Zelnik-Manor L,Perona P.Self-tuning spectral clustering[J].Advances in Neural Information Processing Systems,2004,17:1601-1608. [14] Li D,Wang S,Gan W,et al.Data Field for Hierarchical Clustering[J].International Journal of Data Warehousing & Mining,2011,7(4):43-63. [15] Wang S,Wang D,Caoyuan L I,et al.Clustering by Fast Search and Find of Density Peaks with Data Field[J].Chinese Journal of Electronics,2016,25(3):397-402. [16] Wang S,Fan J,Fang M,et al.HGCUDF:Hierarchical Grid Clustering Using Data Field[J].Chinese Journal of Electronics,2014,23(1):37-42. [17] Barany I,Vu V H.Central limit theorems for Gaussian polytopes[J].Annals of Probability,2006,35(4):1593-1621. CLUSTERINGALGORITHMFORCOMPETITIONOFDATAPOTENTIALENERGYANDK-MEANSBASEDONDATAFIELD Xu Jia’nan Zhang Guizhu (SchoolofIOTEngineering,JiangnanUniversity,Wuxi214122,Jiangsu,China) The K-means algorithm uses the Euclidean distance to divide the data points, cannot accurately characterize the data set, and randomly select the clustering center point mechanism, and cannot get good clustering results. In this paper, a clustering algorithm based on data field-based data potential competition and K-means algorithm is proposed. In this algorithm, the concept of data field is defined, and the local minimum distance is used to compete the potential of data aggregation. The optimal truncation distance based on the distribution of data set is extracted by using potential energy entropy. The cluster center point is determined according to the truncation distance and slope, and the K-means clustering is realized. The results of the UCI dataset show that the fusion algorithm has better clustering results. Data competition Data field Potential entropy Slope Complex dataset 2017-03-21。江蘇省自然科學基金項目(BK20140165)。許家楠,碩士生,主研領域:數據挖掘。張桂珠,副教授。 TP18 A 10.3969/j.issn.1000-386x.2017.12.051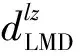
2 DPEC算法的缺陷
3 優化DPEC算法
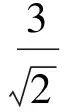
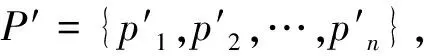
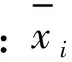
4 K-DPEC算法
5 實驗結果與分析




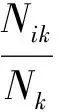
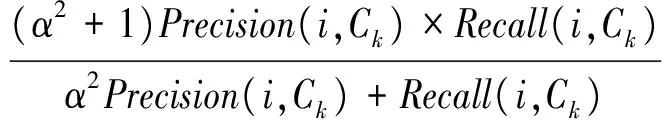
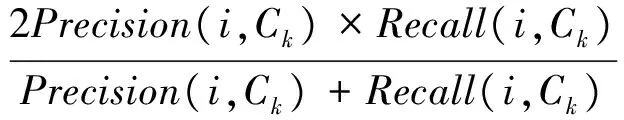
6 結 語

