一種改進的基于核密度估計的DPC算法

仇上正 張曦煌

(江南大學物聯網工程學院 江蘇 無錫 214000)

一種改進的基于核密度估計的DPC算法

仇上正 張曦煌

(江南大學物聯網工程學院 江蘇 無錫 214000)

快速搜索和找到密度峰DPC(clustering by fast search and find of density peaks)的聚類是一種新穎的算法，它通過找到密度峰來有效地發現聚類的中心。 DPC算法的精度取決于對給定數據集的密度的精確估計以及對截止距離dc(cutoff distance)的選擇。dc主要是用于計算每個數據點的密度和識別集群中的邊界點，而DPC算法中dc的估計值卻主要取決于主觀經驗值。提出一種基于核密度估計的DPC方法(KDE-DPC)來確定最合適的dc值。該方法通過引用一種新的Solve-the-Equation方法進行窗寬優化，根據不同數據集的概率分布，計算出最適合的dc。標準聚類基準數據集的實驗結果證實了所提出的方法優越于DPC算法以及經典的K-means算法、DBSCAN算法和AP算法。

概率密度估計 核密度估計 類簇中心 聚類

0 引 言

聚類在知識發現和數據挖掘的領域中起著重要作用。聚類算法試圖將大量數據分配成不同的不相交的類別，其中更相似的數據點被分配到同一群集中，而不相似的數據點被分組到不同的群集中[1]。聚類分析是一種無監督的機器學習方法，在數據挖掘中，有著很重要的應用，在目前是重要的研究方向之一[2]。人們借助聚類分析，不僅可以從大量數據中發現所需的知識與信息，還可以降低工作量，提升工作效率。

目前，世界上存在的聚類算法有層次聚類方法、分層聚類方法、基于密度的聚類方法和基于網格的聚類方法，以及集成式聚類算法。在基于劃分的算法中，K-means算法是目前運用最廣泛的算法之一[3]。然而，嚴重依賴于初始聚類中心使得K-means算法的聚類結果難以滿足目前人們的需求。

首先K-means算法很難發現非凸形狀的簇，對噪聲點和離群點敏感，而且嚴重依賴初始設定的K值。目前，K-means算法存在很大缺陷，文獻[4-6]提出了GKM(Global K-means)算法等一系列改進的方法，來優化K-means算法。

2014年6月，由Alex和Laio在《Science》上發表了一種自動確定類簇數量和類簇中心的新型快速聚類算法，簡稱 DPC[7]。DPC算法存在兩個優點：能快速發現任意形狀數據集的密度峰值點 (即類簇中心)，并且能夠高效進行樣本點分配，還可以快速進行離群點剔除工作。因此，DPC算法適用于大規模數據的聚類分析。然而，該算法存在一個重大的問題，在度量樣本密度的時候，該算法根據主觀經驗，原文作者Alex選擇2%作為截斷距離參數dc的值，對聚類結果影響較大，可能丟失聚類中心，也可能無法識別所有核心點。

為了彌補該算法的不足，本文提出了一種改進的基于核密度估計的DPC算法(KDE-DPC)。為了減少因人為經驗選取截斷距離參數dc的因素對聚類結果造成的影響，在計算核密度的時候，我們通過引用一種新的Solve-the-Equation方法[8]來進行窗寬優化，然后設計一套迭代算法得出最優窗寬，利用最優窗寬從而產生較好的核密度估計結果。該方法避免了人工輸入經驗參數dc值的弊端，根據不同數據集，自動計算出最優窗寬，提高了核密度計算的準確性，同時還提高了樣本分配邊界點的結果。實驗結果表明，該算法能夠提高聚類的準確性，能準確識別所有聚類中心，還能更好地分配邊界點。

1 相關研究

1.1 DPC算法

快速搜索和發現樣本密度峰值的聚類算法(DPC)能自動發現數據集樣本的類簇中心, 實現任意形狀數據集樣本的高效聚類。其基本原理是:理想的類簇中心(density peaks)具備兩個基本特征:1) 與鄰居數據點相比，類簇的中心點具有更大的密度;2) 與其他數據點相比，類簇中心點之間的距離相對較大。對于一個數據集，DPC 算法引入了樣本i的局部密度ρi和樣本i到局部密度比它大且距離它最近的樣本j的距離δi，來找到同時滿足上述條件的類簇中心，DPC算法的有效性很大程度上取決于密度和dc的準確估計。其定義如式(1)和式(2)所示:

(1)

其中:dij為樣本i,j之間的歐氏距離，dc為截斷距離，當x<0時，χ(x)=1，否則χ(x)=0。

δi=minj:ρj>ρi(dij)

(2)

對于局部密度最大的樣本i，其δi=maxdij。

由式(1)可知,文獻[7]引入的樣本局部密度受截斷距離dc影響。DPC算法中dc的選擇基于啟發式方法。數據集中的每個點鄰居的平均數量應該僅為整個數據集的1%～2%。因此，截斷距離dc與用戶關于數據集性質的觀察有關。為了避免截斷距離對樣本局部密度乃至聚類結果的影響, DPC 算法采用指數核[13]計算樣本密度：

(3)

根據聚類心中定義，聚類中心有較大的密度ρi和較大的距離δi。選取28個據點以遞減的密度順序顯示在圖1中。根據計算每個數據點的值畫出決策圖，如圖2所示。

圖1 數據點分布圖

圖2 聚類中心決策圖

從決策圖中可以發現點1和10具有較大的密度值和距離值，根據聚類中心定義，可以確定這兩個點位聚類中心。由于點26、27和28是孤立的，它們具有較高的δ和較低的ρ，可以被認為是噪聲或異常值。 因此，使用決策圖，可以容易地識別出期望的聚類中心。 在成功識別聚類中心之后，DPC算法基于它們在單個回合中的δ值，將剩余的數據點分配給最近的聚類中心，從而完成聚類。

1.2 核密度估計

核密度估計，是一種用于估計概率密度函數的非參數方法[9]，為獨立同分布F的n個樣本點，設其概率密度函數為f，核密度估計為公式：

(4)

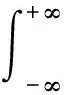
高斯核密度估計是一種常用的核密度估計方法：

(5)

式(5)的性能在很大程度上取決于窗寬h的選擇。均方積分誤差被用來衡量估計h的最佳標準：

(6)

高斯核密度估計具有一些限制，例如，敏感的參數h(帶寬)難以選擇、邊界偏置，以及欠平滑或過平滑等缺點。

2 改進的DPC算法

針對上述DPC算法的問題，本文提出一種改進的基于核密度估計的密度峰快速聚類算法(KDE-DPC)。該算法包括各步驟：

(1) 計算出核密度的最佳帶寬h；

(2) 根據h計算每個點的密度ρ；

(3) 計算出每個點的距離δ；

(4) 畫出決策圖；

(5) 從決策圖中選取聚類中心；

(6) 將點分配給聚類中心；

(7) 檢查邊界點，形成聚類簇。

2.1 最優帶寬h的選擇

由文獻[8]給出的核指數密度計算公式和核密度估計函數公式可以發現，dc相當于核密度估計函數公式中的窗寬h，我們想要得到最優的dc，可以轉變為得到最優的窗寬h。

上面提到評價h優劣的標準為MISE，在弱假設下，其中AMISE為漸進的MISE,而AMISE如下：

(7)

為了使MISE最小，則轉化為求極小值問題，如下：

(8)

其中:

通過式(8)得：

(9)

對于高斯核函數，R(K)=1，m2(K)=1。對于R(f″),我們引入一種新的方法Solve-the-Equation方法對R(f″)求解得：

(10)

由于式(10)中，在最優化hopt的表達式中含有未知量h，因此，我們設計一套迭代算法來計算最優的窗口值。令hopt=F(h),則計算最優窗口寬度值如下：

Step1h1=F(h0),h0=s,對于s的初始值我們對在后面闡述。初始化參數k，其中k為一極小值。

Step2當|h1-h0|>k時，循環執行下面步驟：

(1) 將h1的值賦給h0，即執行h0=h1；

(2) 對于新的h0值，利用表達式h1=F(h0)計算出新的h1值；

Step3返回窗口寬度最優值hopt=h1。

對于s的確定，我們采用如下標準：

其中:n為樣本觀察值的個數，σ為樣本觀察值的標準差。

2.2 算法性能分析

本文改進的算法復雜度主要由下面幾個方面決定：1) 計算樣本之間的距離，此過程的時間復雜度為O(n2)；2) 計算hopt，時間復雜度為O(n2)；3) 迭代求出最優h，時間復雜度為O(n)。

因此經過對比分析，相比于原算法，改進后的算法復雜度一樣。

3 實驗結果與分析

3.1 人工數據集實驗結果分析

為了評估我們提出的KDE-DPC方法的效果，我們將提出方法的實驗結果與DPC算法的結果作對比。所用的人工數據集如表1所示。DPC 算法是文獻[7]作者提供的源代碼。本文KDE-DPC算法采用 Matlab R2010a實現。本實驗的所有實驗運行環境均為Win 8 64 bit操作系統,Matlab R2010a軟件,12 GB內存,Intel(R) Core(TM)2 Quad CPU I5-5200U@2.7 GHz。

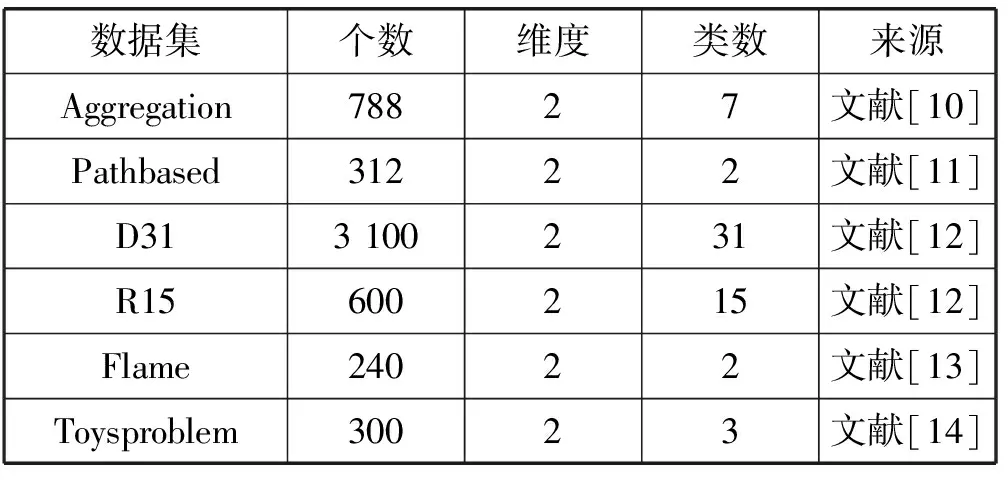
表1 數據集的基本信息

為了能更全面地展現本算法的效果，我們采用對比實驗來分析算法。圖3展現的是提出的KDE-DPC算法與DPC算法分別在D31數據集和R15數據集上做縱向對比實驗的結果。

圖3 DPC算法與KDE-DPC算法對R15數據集和D31數據集的聚類結果

從圖3中，我們可以發現提出的KDE-DPC算法能夠更好地處理噪聲點，準確分配樣本點。

表2展示了本文提出的KDE-DPC算法與DPC算法在識別聚類點和錯誤分類點方面的詳細比較。從表中可以發現KDE-DPC算法無論數據集的性質如何，都能準確識別聚類群的核心點。

表2 對比DPC和KDE-DPC檢測核心點和錯誤點的分類情況

因此，本文提出的KDE-DPC算法是一種能適用于不同數據集的有效的聚類通用解決方案。

3.2 真實數據集實驗結果分析

本文還采用真實的UCI數據集來驗證改進的KDE-DPC算法的聚類性能，并采用Acc、AMI和ARI三個聚類指標來做綜合評價。表3給出了本文KDE-DPC算法，以及對比算法DPC、AP、K-means、DBSCAN算法在真實UCI數據集上的聚類結果。

表3 DPC、AP、K-means、DBSCAN算法在真實UCI數據集上的實驗結果

從表3中可以明顯看出我們提出的KDE-DPC算法在Acc、AMI和ARI三項指標明顯優越于DPC、AP、DBSCAN，以及K-means等經典算法。

總之，本文提出的KDE-DPC算法在復雜度上與DPC算法相同，但在精度上明顯優越于DPC算法以及其他經典算法。

4 結 語

DPC算法思想新穎，而且簡單快速的特點。算法效率上明顯優越于其他經典算法，但是在參數dc的選擇上有很大的缺點。本文通過基于核密度估計優化的思想改進了該算法，達到了不錯的效果。并且，通過對人工數據以及真實數據的測試，驗證了本算法的優點。

在決策圖中，需要人工肉眼來選擇聚類中心，在很多情況下，聚類中心難以分辨，容易造成錯誤的聚類中心或者聚類中心的缺失。未來，我們將進一步優化該算法，能夠實現自動準確選取聚類中心的功能。

[1] Han J W,Kamber M.Data Mining Concepts and Techniques[M].2nd ed.New York:Elsevier Inc,2006:383-424.

[2] Lu J,Liong V E,Zhou X,et al.Learning Compact Binary Face Descriptor for Face Recognition[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2015,37(10):2041-2056.

[3] Jain A K.Data Clustering:50 Years Beyond K-means[M]//Machine Learning and Knowledge Discovery in Databases.Springer Berlin Heidelberg,2008:651-666.

[4] Likas A,Vlassis N,Verbeek J J.The global k-means clustering algorithm[J].Pattern Recognition,2003,36(2):451-461.

[5] Xie J,Jiang S,Xie W,et al.An Efficient Global K-means Clustering Algorithm[J].Journal of Computers,2011,6(2):271-279.

[6] Ester M,Kriegel H P,Sander J,et al.A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of ACM SIGKDD’96,Portland,1996:226-231.

[7] Rodriguez A,Laio A.Machine learning.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[8] Alexandre L A.A Solve-the-Equation Approach for Unidimensional Data Kernel Bandwidth Selection[OL].2008.http://www.di.ubi.pt/～lfbaa/entnetsPubs/bandwidth.pdf.

[9] Alan Julian Izenman.Review Papers:Recent Developments in Nonparametric Density Estimation[J].Journal of the American Statistical Association,1991,86(413):205-224.

[10] Gionis A,Mannila H,Tsaparas P.Clustering Aggregation[J].Acm Transactions on Knowledge Discovery from Data,2007,1(1):4.

[11] Chang H,Yeung D Y.Robust path-based spectral clustering[J].Pattern Recognition,2008,41(1):191-203.

[12] Veenman C J,Reinders M J T,Backer E.A maximum variance cluster algorithm[J].Pattern Analysis & Machine Intelligence IEEE Transactions on,2002,24(9):1273-1280.

[13] Fu L,Medico E.FLAME,a novel fuzzy clustering method for the analysis of DNA microarray data[J].Bmc Bioinformatics,2007,8(1):3.

[14] Pedregosa F,Gramfort A,Michel V,et al.Scikit-learn:Machine Learning in Python[J].Journal of Machine Learning Research,2011,12(10):2825-2830.

ANIMPROVEDDPCALGORITHMBASEDONKERNELDENSITYESTIMATION

Qiu Shangzheng Zhang Xihuang

(SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi214000,Jiangsu,China)

Clustering by fast search and find of density peaks (DPC) is a novel algorithm that efficiently discovers the centers of clusters by finding the density peaks. The accuracy of DPC depends on the accurate estimation of densities for a given dataset and also on the selection of the cutoff distance (dc). Mainly, dc is used to calculate the density of each data point and to identify the border points in the clusters. However, the estimation of dc largely depends on subjective experience. This paper presents a method based on kernel density estimation (KDE-DPC) to determine the most suitable dc. This method performs window width optimization by referencing a new Solve-the-Equation method. According to the probability distributions of the different data sets, the optimal dc is obtained. The experimental results of standard clustering benchmark data sets confirm that the proposed method is superior to DPC algorithm, as well as classic K-means algorithm, DBSCAN algorithm and AP algorithm.

Probability density estimation Kernel density estimation Cluster center Clustering

2016-12-22。江蘇省產學研合作項目(BY2015019-30)。仇上正，碩士生，主研領域：計算機應用技術。張曦煌，教授。

TP391

A

10.3969/j.issn.1000-386x.2017.12.053