基于距離平方差的目標定位估計算法研究

鄭濱紅

（宜春幼兒師范高等專科學校初等教育學院，江西 高安 330800）

基于距離平方差的目標定位估計算法研究

鄭濱紅

（宜春幼兒師范高等專科學校初等教育學院，江西 高安 330800）

無線傳感器網(wǎng)絡(luò)定位技術(shù)作為無線傳感器網(wǎng)絡(luò)的重要支撐技術(shù)之一，具有很大的實際價值和研究意義。無線傳感器網(wǎng)絡(luò)的目標定位估計技術(shù)主要應用于目標跟蹤和目標運動分析，在工業(yè)領(lǐng)域具有廣闊的發(fā)展前景。無線傳感器網(wǎng)絡(luò)由許多在空間中分布的傳感器組成，這些傳感器能夠測量出傳感器與定位目標之間的距離，但是該觀測距離因為受環(huán)境影響所以是有噪音的。目前基于距離的最小二乘估計的定位算法已得到廣泛關(guān)注，但是該問題是一個非凸問題，精確求解十分困難。因此學者們提出了基于距離平方的最小二乘估計的定位算法，該算法的數(shù)學模型雖然相對精確，但是計算起來十分復雜。本文基于距離平方差，提出了新的目標定位估計算法，該算法計算簡單，穩(wěn)定性強，且能得到與基于距離平方的最小二乘估計的定位算法相當?shù)慕Y(jié)果。仿真實驗結(jié)果表明，無論在低噪音水平、中噪音水平還是高噪音水平下，本文提出的新算法都更有優(yōu)勢，在工程領(lǐng)域有極高的應用價值。

無線傳感器網(wǎng)絡(luò)；距離估計；目標定位；最小二乘

0 引言

無線傳感器網(wǎng)絡(luò)是隨著無線通信、嵌入式技術(shù)、傳感器技術(shù)、微機電技術(shù)及分布式信息處理技術(shù)的進步而發(fā)展起來的一門新興的信息獲取技術(shù)。無線傳感器網(wǎng)絡(luò)的發(fā)展最初起源于戰(zhàn)場監(jiān)測等軍事應用，而現(xiàn)今無線傳感器網(wǎng)絡(luò)被應用于很多民用領(lǐng)域，如環(huán)境與生態(tài)監(jiān)測、健康監(jiān)護、家庭自動化、以及交通控制等。無線傳感器網(wǎng)絡(luò)定位技術(shù)作為無線傳感器網(wǎng)絡(luò)的重要支撐技術(shù)之一，無疑是具有很大的實際研究價值和意義的。無線傳感器網(wǎng)絡(luò)最重要的運用在于目標定位估計，這一技術(shù)主要應用于目標跟蹤和目標運動分析[1-4]。

無線傳感器網(wǎng)絡(luò)由許多在空間中分布的傳感器組成，由于傳感器具有體積小、價格低、自組織、隱蔽性好等特點，同時還兼?zhèn)錈o線通信及網(wǎng)絡(luò)隨機部署等功能，因此非常適合用于目標的定位和跟蹤。在無線傳感器網(wǎng)絡(luò)中有一個輻射目標源，該目標源向周圍輻射信號，同時無線傳感器網(wǎng)絡(luò)中的傳感器接收目標源的信號，傳感器能夠基于接收信號測量出傳感器與定位目標之間的距離，但是該觀測距離因為受環(huán)境影響所以是有噪音的。近年來，利用傳感器的測量距離來定位一個輻射目標源的位置坐標的問題已經(jīng)在信號處理領(lǐng)域引起了極大的關(guān)注[5-7]。

基于距離的最小二乘估計的定位算法已得到廣泛關(guān)注，該算法的模型本質(zhì)上是對目標定位的最大似然估計[5],但是該問題是一個非凸問題，精確求解十分困難[6-7]。因此 Beck等人提出了基于距離平方的最小二乘估計的定位算法，該算法能夠計算出一個不錯的定位，但是計算過程過于復雜[6]。本文基于距離的平方差，提出了新的目標定位估計算法，該算法計算簡單，穩(wěn)定性強，且能得到與基于距離平方的最小二乘估計的定位算法相當?shù)慕Y(jié)果。無論在低噪音水平、中噪音水平還是高噪音水平下，新算法相比 Beck等人提出的計算十分復雜的算法都更有優(yōu)勢。

1 基于距離的目標定位估計

1.1 物理模型介紹

本文考慮在空間中分布的m個傳感器，用s∈Rn表示第i個傳感器的坐標向量（在實際場景

1.2 基于距離的最小二乘估計模型

估計目標源位置的坐標向量的最基本的方法是基于距離觀測值ir的最小二乘（range-based least squares，RLS）估計模型：

（RLS）問題的最優(yōu)解稱為目標源坐標的基于距離的最小二乘估計。特別地，當ε服從高斯分布，且協(xié)方差矩陣與單位矩陣成比例時，（RLS）問題的最優(yōu)解事實上就是對目標源坐標的最大似然估計[5]。（RLS）問題是非凸的，所以找到它的精確解是十分困難的。為求解該問題，人們通過半正定松弛技術(shù)將（RLS）問題轉(zhuǎn)化為半定規(guī)劃問題[5]。半定規(guī)劃問題可利用內(nèi)點法[8]在多項式時間內(nèi)有效求解。但是，半定規(guī)劃問題得到的最優(yōu)解并不是（RLS）問題的最優(yōu)解，該算法有時會得到很差的估計定位。所以人們開始嘗試構(gòu)造不同的模型來得到更好的定位算法。

1.3 基于距離平方的最小二乘估計算法

估計目標源位置的坐標向量的另一種方法是基于距離觀測值ir的平方的最小二乘（squared-rangebased least squares，SRLS）估計模型：

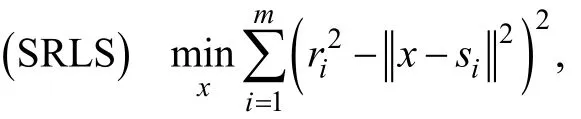
（SRLS）問題的最優(yōu)解稱為目標源坐標的基于距離平方的最小二乘估計。注意到，（SRLS）問題的最優(yōu)解只是對目標源坐標的最大似然估計的次優(yōu)解，因為平方誤差的協(xié)方差矩陣與單位矩陣不成比例[9]。與（RLS）問題一樣，（SRLS）問題也是非凸的，但是Beck等人提出了求解該問題的可執(zhí)行的算法[6]。（SRLS）問題等價于如下的約束優(yōu)化問題：

進一步地，令：

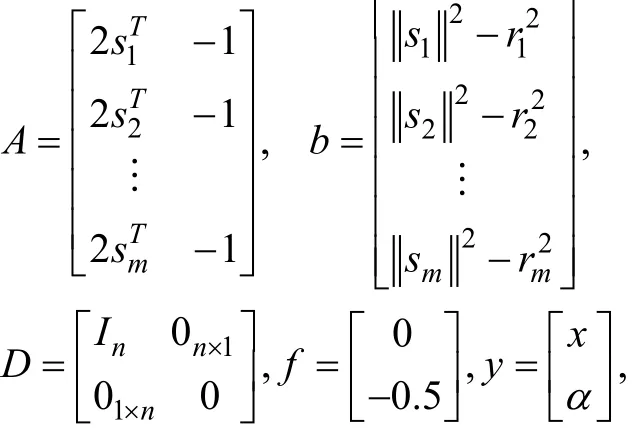
則（SRLS）問題可寫成如下的形式：

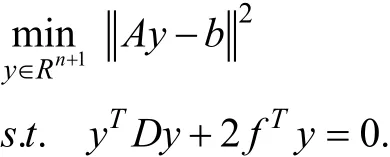
Beck等人提出了求解（SRLS）問題的算法如下[6]：

算法1：Beck求解（SRLS）問題的算法

步驟1：計算矩陣 A , D，計算向量 b, f。

步驟 4：目標源坐標的基于距離平方的最小二乘估計為y?(λ0)的前n項，即

算法1雖然能夠計算出一個不錯的定位，但是計算過程過于復雜。所以我們在下一節(jié)中將提出一個既能計算簡單又能達到定位精度的新算法。

1.4 基于距離平方差的最小二乘估計新算法

假設(shè)無線傳感器網(wǎng)絡(luò)中第1個傳感器位于坐標原點，那么我們可以得到估計目標源位置的坐標向量的新方法：基于第i個傳感器與第 1個傳感器的距離觀測值的平方差（squared-range-difference，SRD），利用最小二乘（least squares，LS）策略來估計目標源的坐標向量x，即求解如下的優(yōu)化問題：

其中：

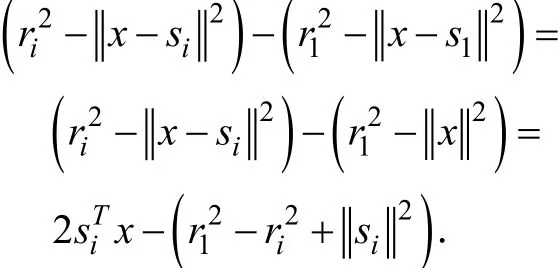
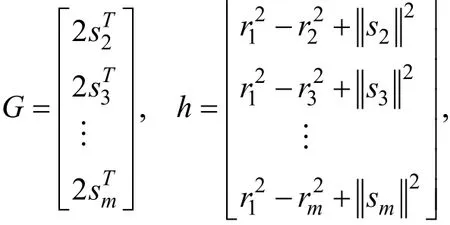
令：則（SRDLS）問題可寫成如下形式：

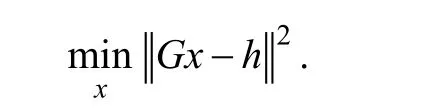
算法2：基于距離平方差的最小二乘估計新算法

步驟1：計算矩陣G與向量h。

雖然（SRDLS）模型沒有（SRLS）模型精確，但是本文基于（SRLS）模型提出的新算法計算簡單，穩(wěn)定性強，在工程領(lǐng)域有極高的應用價值。

2 數(shù)值實驗

例1：考慮在2維平面［- 1 0 ,10］ ×［- 1 0 ,10］平方米的傳感器網(wǎng)絡(luò)中有6個傳感器，他們的位置坐標 si，每個傳感器與定位目標之間的真實距離r?i以及觀測到的噪音距離 ri如表 1所示，其中，觀測距離都在很低的噪音水平上。目標源的實際坐標為x=［4.8509, - 1 .5133］T，利用算法1得到的基于距離平方的最小二乘估計為差為：

此時，本文提出的基于距離平方差的最小二乘估計新算法對目標源的坐標估計更準確。

例2：考慮在2維平面［- 1 0 ,10］ ×［- 1 0 ,10］平方米的傳感器網(wǎng)絡(luò)中有4個傳感器，他們的位置坐標 si，每個傳感器與定位目標之間的真實距離以及觀測到的噪音距離 ri如表 2所示，其中，觀測距離都在很高的噪音水平上。目標源的實際坐標為x=［-1 .2992,- 8 .1697］T，利用算法1得到的基于距離平方的最小二乘估計為誤差為

表1 例1的傳感器坐標、真實距離與噪音距離Tab.1 Position of sensors, exact distances, and observed noisy distances in Example 1

此時，Beck等人提出的基于距離平方的最小二乘估計對目標源的坐標估計特別差，本文提出的基于距離平方差的最小二乘估計新算法對目標源的坐標估計更準確。

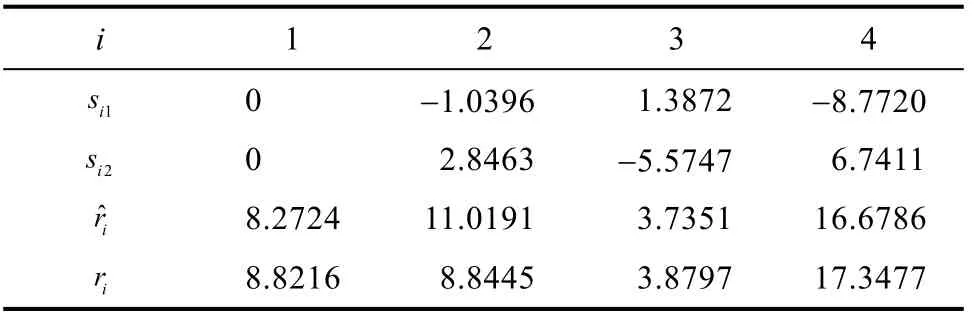
表2 例2的傳感器坐標、真實距離與噪音距離Tab.2 Position of sensors, exact distances, and observed noisy distances in Example 2

除此之外，我們還進行了蒙特卡洛隨機實驗來對比Beck等人提出的算法1與本文提出的算法2，并觀察每個算法隨著傳感器個數(shù)增多時的表現(xiàn)。在仿真實驗中，我們假設(shè)每個距離觀測值的噪音εi為高斯噪聲，滿足 N ( 0,σ2) 的高斯分布。每次實驗都在 2維平面 ［-1 0 ,10 ］ ×［-1 0 ,10］平方米的傳感器網(wǎng)絡(luò)內(nèi)定位一個目標源，每一次實驗中目標源的坐標都在 ［-1 0 ,10 ］ ×［-1 0 ,10］平方米的正方形區(qū)域內(nèi)均勻地隨機選取，同時這m個傳感器的坐標也在［-1 0 ,10］×［- 1 0 ,10］平方米的正方形區(qū)域內(nèi)均勻地隨機選取（每次實驗都設(shè)定 s1= [ 0,0]T），并且每個傳感器的距離觀測值的噪音εi在N ( 0,σ2) 的高斯分布上隨機選取。這里，我們采用均方誤差（root mean square error，RMSE）作為算法的評價標準：

其中，Mc為蒙特卡洛隨機實驗的次數(shù)，本文選擇 M c= 10000，為第i次實驗中對目標源的實際坐標 xi的定位估計。

表3 時算法1與算法2的均方誤差Tab.3 RMSEs of Algorithm 1 and Algorithm 2： -6

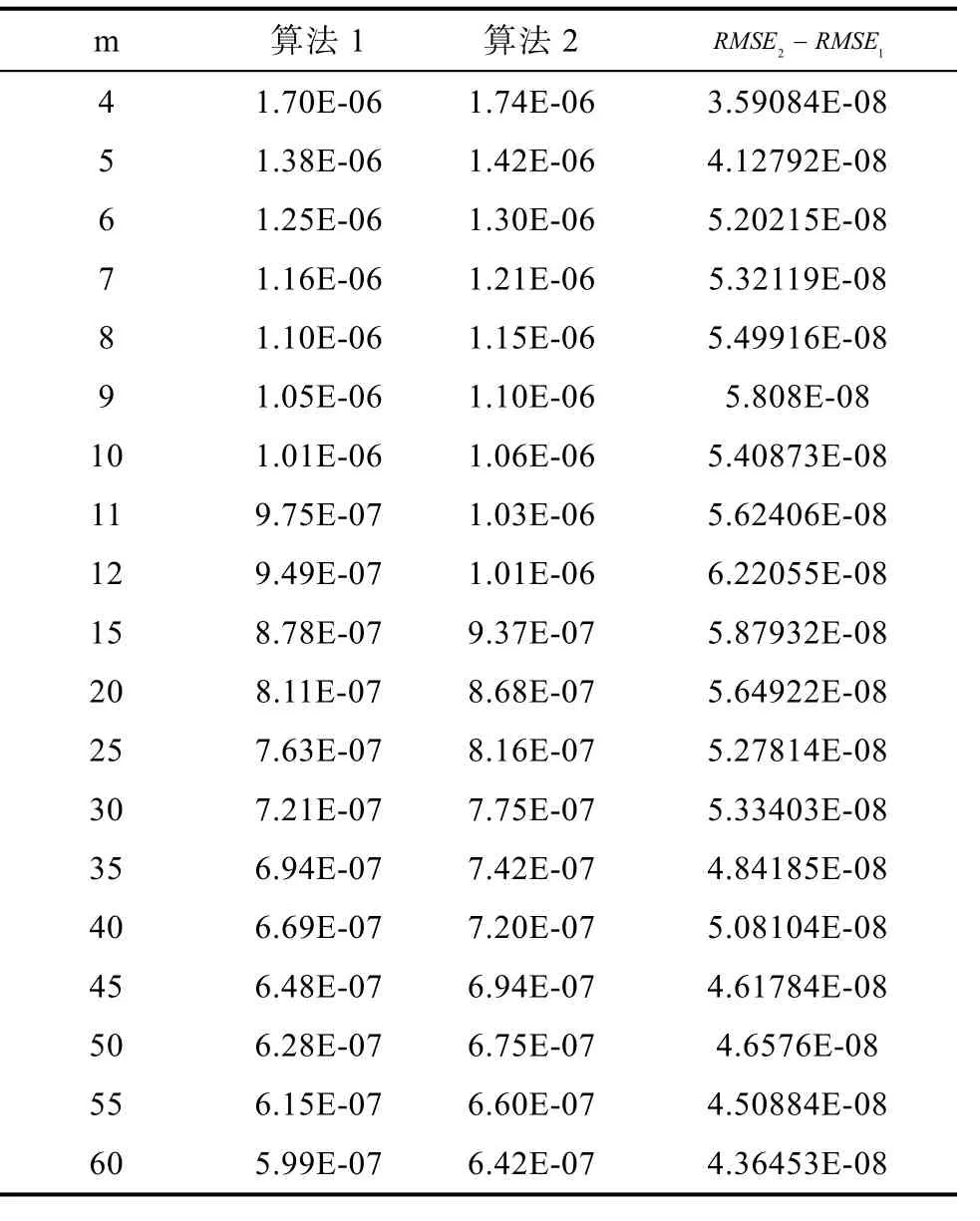
表3 時算法1與算法2的均方誤差Tab.3 RMSEs of Algorithm 1 and Algorithm 2： -6

m 算法1 算法2RMSE RMSE-2 1 4 1.70E-06 1.74E-06 3.59084E-08 5 1.38E-06 1.42E-06 4.12792E-08 6 1.25E-06 1.30E-06 5.20215E-08 7 1.16E-06 1.21E-06 5.32119E-08 8 1.10E-06 1.15E-06 5.49916E-08 9 1.05E-06 1.10E-06 5.808E-08 10 1.01E-06 1.06E-06 5.40873E-08 11 9.75E-07 1.03E-06 5.62406E-08 12 9.49E-07 1.01E-06 6.22055E-08 15 8.78E-07 9.37E-07 5.87932E-08 20 8.11E-07 8.68E-07 5.64922E-08 25 7.63E-07 8.16E-07 5.27814E-08 30 7.21E-07 7.75E-07 5.33403E-08 35 6.94E-07 7.42E-07 4.84185E-08 40 6.69E-07 7.20E-07 5.08104E-08 45 6.48E-07 6.94E-07 4.61784E-08 50 6.28E-07 6.75E-07 4.6576E-08 55 6.15E-07 6.60E-07 4.50884E-08 60 5.99E-07 6.42E-07 4.36453E-08

從表3、表4和表5的數(shù)值結(jié)果可以看出，雖然新算法2的（SRDLS）模型沒有算法1的（SRLS）模型精確，但是無論在低噪音水平中噪音水平還是在高噪音水平σ=1下，算法2總能達到和算法1相當?shù)亩ㄎ痪取Ｔ诘驮胍羲较拢疚奶岢龅男滤惴?在傳感器個數(shù)較少（ m ≤ 8 ）或者傳感器個數(shù)較多時定位效果十分接近算法 1，這時利用本論文提出的新算法2進行定位既計算簡單又效果良好，相比計算十分復雜的算法1更有優(yōu)勢。在中、高噪音水平下，本文提出的新算法2在傳感器個數(shù)較多時定位效果較接近算法 1，這時利用本論文提出的算法2進行定位既計算簡單又效果良好，相比計算十分復雜的算法1更有優(yōu)勢。

3 結(jié)論

本文基于距離平方差的最小二乘估計模型：（SRDLS）模型，提出了在傳感器網(wǎng)絡(luò)中定位目標源的位置坐標的新算法：算法 2。雖然（SRDLS）模型沒有 Beck等人提出的基于距離平方的最小二乘估計模型：（SRLS）模型精確，但是本文基于（SRLS）模型提出的算法1計算簡單，穩(wěn)定性強且能得到與（SRLS）模型的定位算法1相當?shù)慕Y(jié)果。數(shù)值仿真實驗表明，某些時候Beck等人提出的算法1對目標源的坐標估計特別差，但是本文提出的新算法2對目標源的坐標估計準確，效果良好。并且蒙特卡洛隨機實驗的仿真結(jié)果表明，無論在低噪音水平、中噪音水平還是高噪音水平下，新算法2相比Beck等人提出的計算十分復雜的算法1都更有優(yōu)勢。綜上所述，本文提出的基于距離平方差的最小二乘估計模型更簡單，基于該模型提出的新算法 2不僅計算簡單，穩(wěn)定性強，而且效果良好，在工程領(lǐng)域有極高的應用價值。

表4 時算法1與算法2的均方誤差Tab.4 RMSEs of Algorithm 1 and Algorithm 2：

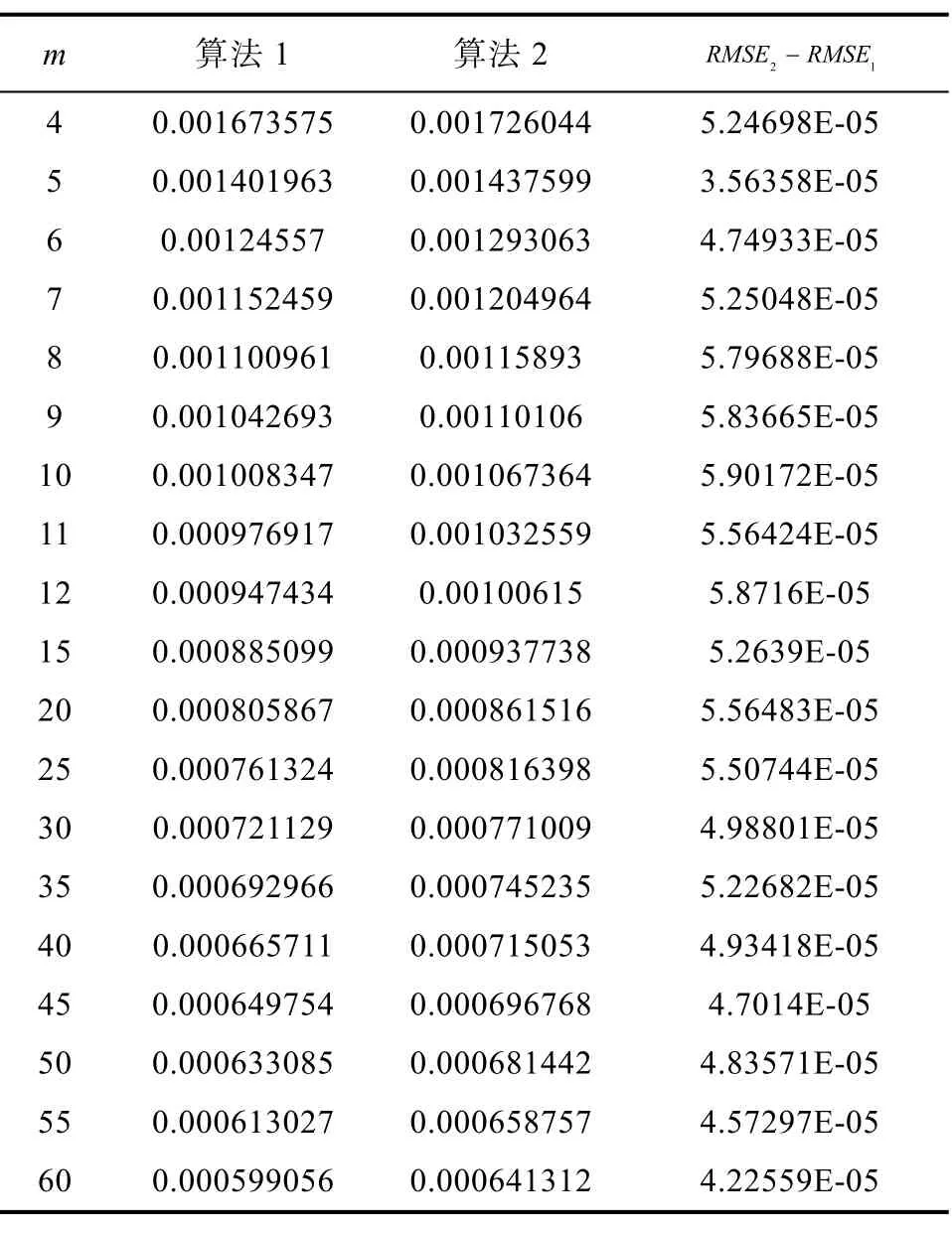
表4 時算法1與算法2的均方誤差Tab.4 RMSEs of Algorithm 1 and Algorithm 2：

m 算法1 算法2RMSE RMSE-2 1 4 0.001673575 0.001726044 5.24698E-05 5 0.001401963 0.001437599 3.56358E-05 6 0.00124557 0.001293063 4.74933E-05 7 0.001152459 0.001204964 5.25048E-05 8 0.001100961 0.00115893 5.79688E-05 9 0.001042693 0.00110106 5.83665E-05 10 0.001008347 0.001067364 5.90172E-05 11 0.000976917 0.001032559 5.56424E-05 12 0.000947434 0.00100615 5.8716E-05 15 0.000885099 0.000937738 5.2639E-05 20 0.000805867 0.000861516 5.56483E-05 25 0.000761324 0.000816398 5.50744E-05 30 0.000721129 0.000771009 4.98801E-05 35 0.000692966 0.000745235 5.22682E-05 40 0.000665711 0.000715053 4.93418E-05 45 0.000649754 0.000696768 4.7014E-05 50 0.000633085 0.000681442 4.83571E-05 55 0.000613027 0.000658757 4.57297E-05 60 0.000599056 0.000641312 4.22559E-05

表5 1σ=時算法1與算法2的均方誤差Tab.5 RMSEs of Algorithm 1 and Algorithm 2： 1σ=

[1] 李杰, 李振波, 陳佳品. 一種基于遺傳算法與蟻群算法混合算法的無線傳感器網(wǎng)絡(luò)定位算法[J]. 軟件, 2017, 38(1)：11-15.

[2] 周唯, 劉冬, 劉會師. 基于無線傳感器網(wǎng)絡(luò)拓撲的研究與設(shè)計[J]. 軟件, 2013, 34(12): 22-25.

[3] 任豐源, 黃海寧, 林闖.無線傳感器網(wǎng)絡(luò)[J]. 軟件學報,2006, 14(7): 1282-1290.

[4] 王福豹, 史龍, 任豐源. 無線傳感器網(wǎng)絡(luò)中的自身定位系統(tǒng)和算法[J]. 軟件學報, 2005, 16(5): 857-868.

[5] CHEUNG K W, MA W K, SO H C. Accurate approximation algorithm for TOA-based maximum likelihood mobile location using semidefinite programming[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing,2004. Proceedings. IEEE, 2004, 2: 145-148.

[6] BECK A, STOICA P, LI J. Beck, A., Stoica, P., & Li, J.(2008). Exact and approximate solutions of source localization problems[J]. IEEE Transactions on Signal Processing, 2008,56(5): 1770-1778.

[7] CHEN S, HO K C. Achieving asymptotic efficient performance for squared range and squared range difference localizations[J]. IEEE Transactions on Signal Processing, 2013,61(11): 2836-2849.

[8] VANDENBERGHE L, BOYD S. Semidefinite programming[M]. Society for Industrial and Applied Mathematics, 1996.

[9] CHEUNG K W, SO H C, MA W K, et al. Least squares algorithms for time-of-arrival-based mobile location[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 1121-1130.

A Squared-Range-Difference-Based Least Squares Estimation Algorithm of Source Localization Problems

ZHENG Bin-hong
(School of Primary education, Yichun infant normal college, Gaoan 330800, Jiangxi)

As one of the important support technologies of wireless sensor networks, wireless sensor network location technology has great practical value and research significance. The technology of target location estimation in wireless sensor networks is mainly used in target tracking and target motion analysis, which has broad prospects in the industrial field. Wireless sensor network consists of many spatially distributed sensors, these sensors can measure the range between the sensors and the target, but the observed range is with noise caused by the environment. At present, the localization estimation algorithm based on the range least squares estimation has drawn much attention, but the problem is a non-convex problem, so it is very difficult to exactly solve the problem. Therefore,scholars have proposed localization estimation algorithm based on least squares of the range squares. Although the mathematical model of that algorithm is relatively accurate, its computation is very complex. Based on the range square difference, a new targeting estimation algorithm has proposed in this paper, and the new algorithm is simple,is with high stability, and can reach nearly same good results as the algorithm based on the range least squares estimation. Simulation results show that the new algorithm proposed in this paper have more advantages than the other algorithm under low noise levels, medium noise levels, and high noise levels. Thus the new targeting estimation algorithm proposed in this paper has a very high value in the engineering field.

Wireless sensor network; Distance estimation; Source localization; Least squares

TP212.9

A

10.3969/j.issn.1003-6970.2017.12.054

本文著錄格式：鄭濱紅. 基于距離平方差的目標定位估計算法研究[J]. 軟件，2017，38（12）：270-274

鄭濱紅(1988-)，女，講師，主要研究方向：科學計算。